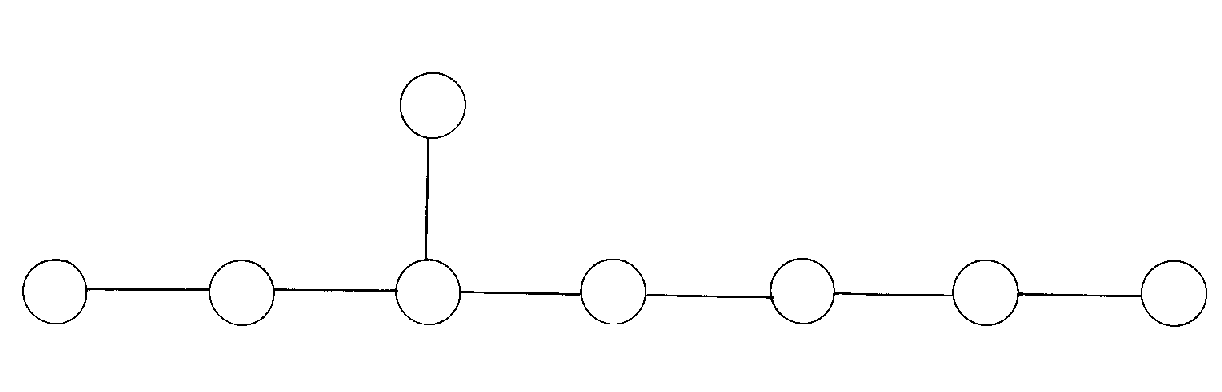
Now let's try taking the Dynkin diagram of the biggest exceptional Lie algebra, and keep removing the right most dot, and see what happens. You start with E₈.

This group is important in superstring theory. Now remove the right most dot, and you get E₇.

Now do the same thing again, and you get E₆.

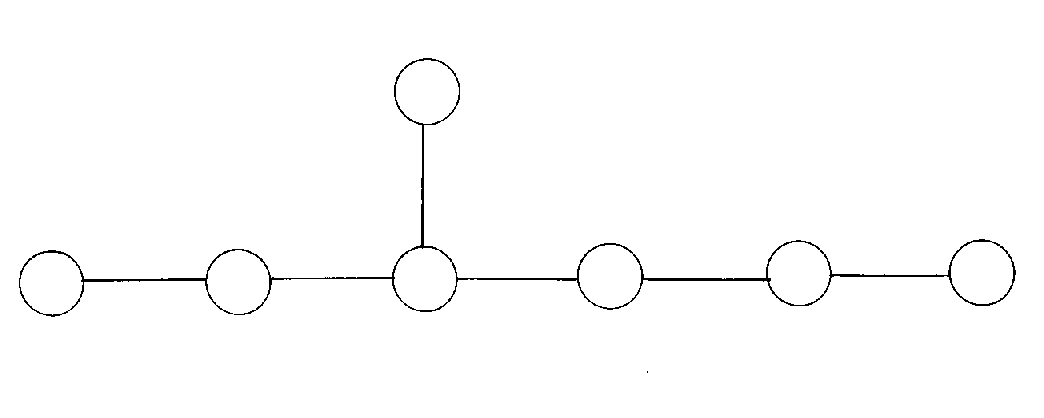
E₆ is used in grand unified theories. Remove the right most dot again.

This is SO(10) which is used in grand unified theories. Remove the right most dot again.

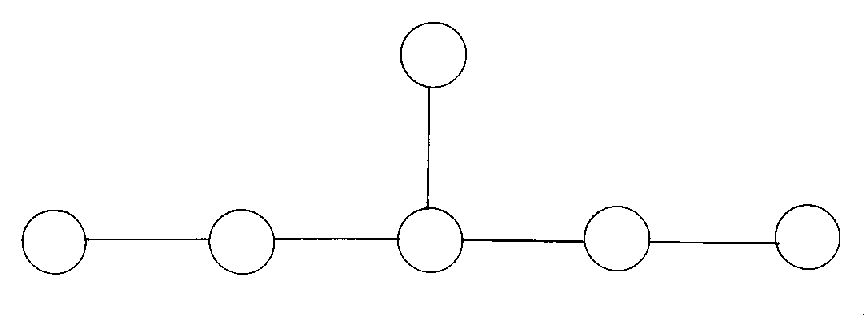
This is SU(5) from grand unified theory. Now remove the right most dot from the line of dots we were removing them from.

This is the SU(3) x SU(2) group of the Standard Model. Notice that just by repeatedly removing the right most dot, we continually get groups that are important in particle physics. First E₈, then E₆, SO(10), SU(5), and the Standard Model. You take the largest possible exceptional group, and repeatedly remove the right most dot, and you will get only groups important in particle physics, except for E₇, and you will get all the groups important in particle physics, except for SO(32). This has to do with the fact that in grand unified theory, the groups are nestled within each other, and each group is contained in a larger group. As you go through symmetry breaking, you go from larger to smaller groups.

The quarks and leptons can be united in grand unified theories. However, a more ambitious goal is to unite the two broadest categories of particles, which are the fermions and bosons. This is called supersymmetry, or SUSY. There are several reasons for supporting supersymmetry beyond the aesthetic appeal of unifying the fermions and bosons. Most important is the problem of quadratic divergences, which are contributions to the mass of the Higgs particle, which drive up the Higgs mass to unacceptable levels, violating the unitarity condition. This is called the hierarchy problem. In supersymmetry, contributions from both fermions and bosons cancel out, leaving a much smaller Higgs mass, thereby solving the hierarchy problem. In grand unified theories, the coupling constants almost converge but not quite. In supersymmetry, they exactly converge. In an extension of supersymmetry called supergravity, there is a natural way of including gravity, although it doesn't solve the problem of renormalization. Lastly, the lightest supersymmetric particle should be stable, and is thus a candidate for dark matter.

In supersymmetry, every fermion is associated with a boson that's name is the same except begins with "s-", and with a spin that is ½ less. Every boson is associated with a fermion that's name is the same except ends with "-ino", and with a spin that is ½ less. Therefore, the electron is associated with the selectron, which has spin 0. The photon is associated with the photino, which has spin ½. The other quantum numbers are the same. Supersymmetric particles are represented by a tilda over the letter.

Supersymmetry was invented independently by several people with different motivations. In 1971, Soviet physicists Yuri Gol'fand and E. Lictman came up with an early theory while trying to introduce parity violation into quantum theory. In 1972, Volkov and Akulov were trying to answer the question as to whether Goldstone bosons with half spin exist. However, most people agree that the main inventors of supersymmetry were Julius Wess and Bruno Zumino in 1974, who were performing a generalization of the subgroup which first appeared in the Neveu-Schwarz-Ramond model, thereby discovering quantum field theories with spacetime supersymmetry in four spacetime dimensions.

Let's look at the hierarchy problem in more detail since it is the main motivation for supersymmetry. A phenomenological field theory such as the Standard Model must be cut off at small distances to be defined. The formal path integral is meaningless until a prescription is given for regularizing its short distance behavior. This prescription specifies a momentum k as a cut off, and a set of parameters including coupling constants g, and a mass parameter u, which will generally depend on k. Of course, there exist quantum fluctuations less than the wavelength but the whole point of renormalization is that these effects can be lumped into the various values of the constants g and u. A change in the cutoff from k to k' can be compensated by a change in g and u. In this way, the Standard Model can deal with changes to the parameters that result from virtual particles constantly be emitted and reabsorbed by bosons and fermions, but not the Higgs particle. The mass of the Higgs would be driven up to unacceptable levels. This is because the Higgs two-point function contains not just logarithmic but also quadratic divergences. This causes the Higgs mass to be so high that it violates unitarity. This is the hierarchy problem. What actually causes these corrections to the masses of the particles? The measured electron mass is a combination and the bare mass and the self-energy, which is the result of the electron emitting and reabsorbing virtual photons. Therefore, the correction to the mass is caused by the self-energy which is caused by the loop diagrams of virtual particles. However, the loop diagrams of virtual fermions and bosons have the opposite effect. In supersymmetry, there's a boson for every fermion, and vice versa, so these loop diagrams cancel each other out, so you don't have the very large correction term for the Higgs mass.

In my paper on the Standard Model, I skipped over some of the details of quantum field theory, so let me just briefly review them. In quantum field theory, you want the wavefunction of a particle to only propagate forward and not backwards in time. You use Green's function to distinguish between the two arrows of time. If you have a scalar field wave equation with a delta function source

([D'Alambertian] + m²) G = -[delta]⁽⁴⁾ (x^u - x'^u)

the Green function G(x^u, x'^u) that solves this equation is found by going to momentum space, where

[delta]⁽⁴⁾ = [integral] (d⁴/(2[pi])⁴) e^-ikx

This gives the Feynman propagator

G_F = 1/(k² - m² + i[epsilon])

where k is momentum, m is mass, and the small positive ε is set to zero after performing momentum space integrations. This then gives you the propagator for the scalar field

<0|T[[phi](x) [phi](x')]|0> = i[integral] (d⁴/(2[pi])⁴) e^{-ik(x - x')}(1/(k² - m² + i[epsilon]))

Let's first look at the case of the photon self-energy taking into account the one-loop correction to the Feynman diagram. The photon becomes an electron-positron pair which then turns back into a photon. These examples will be two-point functions, since there are two vertices, at vanishing momentum, computed at one-loop level. The computed quantities correspond to the mass parameters appearing in the Lagrangian, and since we assume vanishing external momentum, this will not be the on-shell pole mass. It is easy to see that the differences between these two quantities can at most involve logarithmic divergences due to wave function normalization. The following shows the photon self-energy in QED.

The following is the photon's two-point function which receives contributions due to the electron-positron loop diagram.

[pi]_{[gamma] [gamma]}^uv (0) = -[integral] (d⁴k/(2[pi])⁴) tr[(-ie[gamma]⁴) (i/[k slash] -m_e) (-ie[gamma]^u) (i/([k slash] - m_e))

[pi]_{[gamma] [gamma]}^uv (0) = -4e² [integral] (d⁴k/(2[pi])⁴) ((2k^u k^v - g^uv (k² - m_e²))/(k² - m_e²)²)

[pi]_{[gamma] [gamma]}^uv (0) = 0

The integral vanishes because of the regularization scheme that preserves gauge invariance, called dimensional regularization. At a deeper level, it's because of the exact U(1) gauge invariance of QED, which says that the photon must be massless in all orders of perturbation theory.

The following shows the electron self-energy in QED.

The electron self-energy correction is given by

[pi]_ee (0) = [integral] (d⁴k/(2[pi])⁴)b(-ie[gamma]_u) (i/[k slash] - m_e) (-ie[gamma]_u) (-ig^uv/k²)

[pi]_ee (0) = -e² [integral] (d⁴k/(2[pi])⁴) (1/(k²(k² - m_e²)) [gamma]_u ([k slash] + m_e) [gamma]^u

[pi]_ee (0) = -4e² m_e [integral] (d⁴k/(2[pi])⁴) (1/(k²(k² - m_e²))

using the fact that the ([k slash] - m_e) term vanishes after integration over angles, if you use a regulator that respects Poincare invariance. The integral in the above equation has a logarithmic divergence in the ultraviolet, meaning at large momenta. Notice that this correction to the electron mass is proportional to the electron mass. Without a cutoff, the correction is infinite, but if you use the Planck scale as the cutoff scale, the mass correction is

[delta]m_e ~ ([alpha]_em/[pi]) m_e (M_pl/m_e) ~ 0.24 m_e

which is a small correction. The reason the loop diagram doesn't change the electron mass by much is due to symmetry. In the limit m_e -> 0, the model becomes invariant under chiral rotations.

[psi]_e -> e^{i[gamma]₅[psi]} [psi]_e

If the symmetry was exact, the mass correction would vanish. Since the symmetry is broken by the electron mass, the mass correction itself must be proportional to m_e.

Now, we'll consider the contributions of fermion loops to the two-point function of the Standard Model Higgs field.

With the Hf[f bar] coupling given by the coupling constant [lambda]_f, the mass correction is given by

[pi]_{[phi] [phi]}^f (0) = -N(f) [integral] (d⁴k/(2[pi])⁴) tr [ (i([lambda]_f/[square root of 2]) (i/[k slash - m_f) (i[lambda]_f/[square root of 2]) (i/[k slash] - m_f)]

[pi]_{[phi] [phi]}^f (0) = -2N(f) [lambda]_f² [integral] (d⁴k/(2[pi])⁴) ((k² + m_f²)/(k² - m_f²)²)

[pi]_{[phi] [phi]}^f (0) = -2N(f) [lambda]_f² [integral] (d⁴k/(2[pi])⁴) [(1/(k² - m_f²)) + (2m_f²/(k² - m_f²)²)]

where the multiplicity factor N(f) is three for quarks, and one for leptons. The first term in the last line of the above equation is quadratically divergent. If you were to use the Planck mass as a cutoff, the resulting correction would be 30 times larger than the Standard Model Higgs mass, which is assumed to be about 1 TeV. If the Higgs mass is much larger than 1 TeV, it would violate the unitarity condition in regards to the WW scattering amplitudes. You can define unitarity as saying the probability of something can't be greater than 1. U U^† = 1 If the Higgs mass is too big, Higgs self-interaction will make the coupling constant bigger than 1. Also, if m_H is too big, the decays H → W W and H → Z Z will have a full decay width as large as the Higgs mass. These are all considered impossible, so the Higgs mass can't be larger than about 1 TeV.

The difference in the size of the mass correction to the electron and the Higgs illustrates the difference between logarithmic and quadratic divergences. Also notice that the correction does not depend on the mass of the Higgs. There is nothing in the Standard Model that protects the mass of the Higgs in the way that the photon and electron masses are protected.

Now you can renormalize the quadratic divergence away. The remaining correction would be of order

N(f) ((m_f² [lambda]_f²)/8[pi])

If the Standard Model were the ultimate theory in physics, and m_f were the mass of the top quark, then the correction would be small. However, nobody thinks the Standard Model is the final theory in physics. It is much more plausible that at some very high energy scale, it will have to be replaced with a more fundamental theory, such as grand unification. In a grand unified theory, m_f would be at the GUT scale, which would cause the correction to be extremely large. Even without grand unification, there is probably new physics at the Planck scale. Now, you can still assume a very large bare mass to cancel out the very large loop corrections, leaving a result of about 1 TeV. However, in that case, you would have to assume the coincidence that these two very large values were so close as to almost cancel out. This is called a fine-tuning problem, which you want to avoid in physics. Let's assume u² (0) has the form

u² (0) = u² (k) + k² (c₁ [lambda] + c₂ g² + …)

Let's assume the cutoff k is at the energy of the GUT scale.

u² (0) = u² (M_GUT) + M_GUT² (c₁ [lambda] (M_GUT) + …)

If M_GUT = 10¹⁵ GeV, this gives

((u² (0))/M_GUT²) = ((u² (M_GUT))/(M_GUT²)) + (c₁ [lambda] + …) = 10^-26

This would require the dimensionless parameter to cancel out the complicated series to 26 decimal places. In other words, this would require enormous fine-tuning which does not seem realistic.

In supersymmetry, you assume that for every fermion, there is an associated boson. You have to take into account the one-loop diagrams of both the fermions and bosons when calculating the correction to the Higgs mass. As it turns out, the effects from these two types of loop diagrams cancel out.

Let's say you have two complex scalar fields [f tilda]_L and [f tilda]_R with the following coupling to the Higgs field

L_{[phi] [f tilda]} = (1/2) [lambda tilda]_{f [phi]} ( | [f tilda]_L |² + | [f tilda]_R |² ) + v[lambda tilda]_f [phi] ( | [f tilda]_L |² + | [f tilda]_R |² ) + (([lambda]_f/[square root of 2) A_f [phi] [f tilda]_L [f tilda]_R* + hermitian conjugate

where v is the vacuum expectation value of the Standard Model Higgs. v = 246 GeV The second term in the Lagrangian is due to the breaking of the SU(2) x U(1), and its coefficient is related to that of the first term. The coefficient of the third term is arbitrary. λ_f is a convention. This Lagrangian gives the following contribution.

[pi]_{[phi] [phi]}^{[f tilda]} (0) = -[lambda tilda]_f N(f) [integral] (d⁴k/(2[pi])⁴) [(1/(k² - m_{[f tilda]_L}²)) + [(1/(k² - m_{[f tilda]_R}²))] + ([lambda tilda]_f v)² N([f tilda]) [integral] (d⁴k/(2[pi])⁴) >) [(1/(k² - m_{[f tilda]_L}²)²) + [(1/(k² - m_{[f tilda]_R}²)²)] + | [lambda]_f A_f |² N([f tilda]) [integral] (d⁴k/(2[pi])⁴) (1/((k² - m_{[f tilda]_L}²)(k² - m_{[f tilda]_R}²))

The first line comes from the first loop diagram, and contains quadratically divergent terms. The quadratic divergences can be made to cancel by choosing

N([f tilda]_L) = N([f tilda]_R) = N(f)

[lambda tilda]_f = -[lambda tilda]_f²

The cancellation of divergences does not impose restrictions on the masses, m_{[f tilda]_L}, m_{[f tilda]_R}, or the coupling constant A_f

[integral] (d²/i[pi]²) (1/(k² - m²)) = m² (1 - log (m²/u²))

[integral] (d²/i[pi]²) (1/(k² - m²)²) = - log (m²/u²))

where u is the renormalization scale. For simplicity, let's assume , m_{[f tilda]_L} = m_{[f tilda]_R} = m_{[f tilda]}. This gives

[pi]_{[phi] [phi]}^{f + [f tilda]} = i(([lambda]_f² N(f))/(16[pi]²)) [-2m_f² (1 - log (m_f²/u²)) + 4m_f² log (m_f²/u²) + 2m_{[f tilda]}² (1 + log (m_f²/u²) + 2m_{[f tilda]}² (1 + log (m_{[f tilda]}²)) - 4m_f² log (m_{[f tilda]}²) - | A_f|² (m_{[f tilda]}²)]

using

m_f = ([lambda]_f v)/[square root of 2]

The first two terms are the fermionic contribution. Therefore, you achieve complete cancellation between the fermionic and bosonic contributions. You achieve a vanishing total correction if you require

m_{[f tilda]} = m_f

A_f = 0

Even if you let m_f go to infinity, the correction will remain small as long as the difference between m_f² and m_{[f tilda]}² remains small, and the coefficient A_f remains small. Therefore, the introduction of the fields [f tilda]_L and [f tilda]_R has not only allowed us to cancel quadratic divergences, but it also shields the weak scale from loop corrections involving heavy particles if the mass splitting between the fermions and bosons itself is at the weak scale. Therefore, supersymmetry solves the hierarchy problem.

I should also mention an alternative explanation for the hierarchy problem called technicolor. This used to be a serious rival to supersymmetry, but it does not work near as well, and so far no one has come up with a version of it that doesn't contradict reality. Still, in order to be knowledgeable about physics beyond the Standard Model, you should be aware of what technicolor is. In a way, technicolor is more accurately described as an alternative to the Higgs mechanism, but of course if there's no Higgs particle, then there's no hierarchy problem. The Higgs mechanism is a way of giving masses to the W⁺, W^-, and Z⁰ bosons. Through the breaking of a global symmetry, the associated goldstone boson becomes the longitudinal component of the W⁺, W^-, and Z⁰ bosons, thereby giving them mass. There are, of course, other examples of spontaneous symmetry breaking, one of which is the chiral symmetry of QCD. In that case, the associated goldstone boson is assumed to be the neutral pion. Could you use the symmetry breaking of the QCD chiral symmetry, SU(2) x U(1), to give mass to the W⁺, W^-, and Z⁰ bosons? Yes, that is possible. The chiral multiplet is isomorphic to the Higgs multiplet. The pion multiplet would mix with the gauge fields, and become the longitudinal component of the W⁺, W^-, and Z⁰. There would be no Higgs particle, and thus no hierarchy problem.

The problem is that the masses of the resulting W⁺, W^-, and Z⁰ would be 2000 times too small. However, let's say you invented a second QCD-like gauge sector called technicolor. This gauge group does not have to be SU(3), and it should become strong at 2000 times the QCD scale. If this sector contains fermions which carry technicolor instead of color, but which form conventional weak doublets, then condensates will induce SU(2) x U(1) breaking. The W⁺, W^-, and Z⁰ will get masses of the correct magnitude, and no very small or fine-tuned parameters are needed. The main prediction of technicolor is the prediction of a spectrum of technihadrons with masses, widths, and splittings 2000 times their hadronic counterparts. So far so good. Unfortunately, there is a serious problem with technicolor which no one has been able to satisfactorily solve, namely that there is no mechanism to give masses to the fermions. Remember that in the Standard Model, the fermion-Higgs interaction terms allow for fermion masses. However, in technicolor, there are no Higgs particles, so you can't do that, and so you have to think of some other way of giving mass to the fermions. One idea called extended technicolor introduces new gauge degrees of freedom, called E, which couple ordinary fermions to technifermions. This ends up giving mass to the fermions. Another idea is that quarks, leptons, and technifermions are all composites of more fundamental particles called preons, bound by yet a third strong interaction called metacolor. The binding energy can give mass to these composite particles. However, all of these ideas conflict with observation in one way or another, for instance, in the prediction of neutral strangeness changing currents, etc. Therefore, technicolor just doesn't seem to work, and supersymmetry won that debate.

In quantum mechanics, energy is quantized, meaning you have discrete energy levels associated with particles.

H_N = [summation over i] N_j [epsilon]_j

where H_N is the Hamiltonian, and N_j is the number of particles in each energy state. Therefore

Q = [summation over N] [integral] e^{((u N - H_N)/kT)} d[capital gamma]_N

Q = [summation over N_j] e^{[summation N_j (u - [epsilon]_j)/kT}

where k is the Boltzmann constant, k = 1.38066 x 10^-23 J/K, and T is the temperature. Then using

e^{[summation] x_j} = [product series over j] e^x_j

you have

Q = [summation over N_j] [[product series over j] y_j^N_j]

where

y_j = e^{((u - [epsilon]_j)/kT)}

using

[summation over N_j] [[pi] [alpha]_j (N_j)] = [product series over j] [[summation over N_j] [alpha]_j (N_j)]

you end up with

Q = [product series over j] [summation over N_j] y_j^N_j

The following power series has the following convergent sum

[summation over N_j from 0 to infinity] y_j^N_j = 1 + y_j + y_j² + … = 1/(1 + y_j)

Q = [product series over j] 1/(1 - y_j)

Therefore

[capital omega] = -k + ln Q = k + [summation over j] ln [1 - e^{(u - [epsilon]_j)/kT}]

N = - [partial derivative of capital omega with respect to u]

where Ω is the grand potential.

N = [summation] (e^{(u - [epsilon]_j)/kT})/(1 - e^{(u - [epsilon]_j)/kT}) = [summation] 1/( e^{(( [epsilon]_j - u)/kT}) - 1)

N_j = 1/( e^{(([epsilon]_j - u )/kT}) - 1)

This is the average occupation number if you can have any number of particles in a single state, meaning not obey the Pauli exclusion principle, in other words, bosons. What if you can have only zero or one particle in each state, meaning particles that obey the Pauli exclusion principle, or in other words, fermions?

Before we considered the possibility that you could have an arbitrary number of particles in any given energy state, and therefore took a summation of every value of N_j from zero to infinity. Now, let's assume N_j can only take two values, zero or one, meaning you only have either zero or one particles in each energy state. If N_j = 0 or 1, then

[summation over N_j from 0 to 1] y_j^N_j = 1 + y_j

so therefore

[capital omega] = -k + ln Q = -kT [summation] ln [1 + e^{((u - [epsilon]_j)/kT)}]

with

N = -[partial derivative of capital omega with respect to u] = [summation] (N_j)

N_j = 1/( e^{(([epsilon] - u )/kT}) + 1)

The above results for bosons and fermions are called the statistics, and give the statistical rules which apply to large numbers of particles. Bosons obey Bose statistics, also called Bose-Einstein statistics, partly named after Satyendra Nath Bose. Fermions obey Fermi statistics, also called Fermi-Dirac statistics, named after Enrico Fermi and Paul Dirac. Notice the above result for fermions is exactly the same result as for bosons except there is a plus sign instead of a minus sign. The Bose statistics have a minus sign, and the Fermi statistics have a plus sign. This is the ultimate reason why the algebra of bosons involves commutators, and the algebra of fermions involves anticommutators. Remember that a commutator is defined as

[a, b] = ab - ba

and an anticommutator is defined as

{a, b} = ab + ba

For normal numbers, [a, b] = 0. However, the only normal number for which {a, b} = 0 is zero. Therefore, we invented entities called Grassmann variables which satisfy {a, b} = 0.

Remember in the electromagnetism section of my paper on the Standard Model, I gave the following relations for the energy of a particle system.

E = [summation] ([h bar]w/2) (a a^† + a^† a)

E = [summation] (N + (1/2)) [h bar]w

where [a, a^†] = 1, and the number operator N = a^† a. Notice the energy is nonzero even if N = 0. Therefore, you have vacuum energy. This is a bosonic field since we quantized via the commutator [a, a^†] = 1. In supersymmetry, every bosonic field is matched by a corresponding fermionic field. The fermionic fields would be quantized via the anticommutator {a, a^†} = 1, which gives

E = (N - (1/2)) [h bar]w