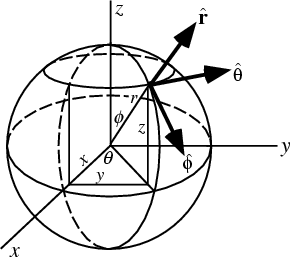

The conversion between spherical and Cartesian coordinates is given by
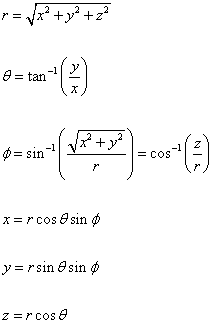
r = [squareroot of (x2 + y2 + z2)]
θ = tan-1 (y/x)
φ = sin-1 ([squareroot of (x2 + y2)]/r) = cos-1 (z/r)
x = r cos θ sin φ
y = r sin θ sin φ
z = r cos θ
You can then define the following line element.
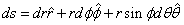
ds = dr[r hat] + rdφ [φ hat] + r sin φ dθ [θ hat]
where the hatted symbols represent the unit vectors. We also want to allow the possibility of any type of curvature, positive, negative, or zero. In the 1920's, Edwin Hubble measured the redshifts of the galaxies, and determined that the Universe is expanding. Therefore, the metric must also include expansion. The time-dependant scale factor is R(t), and you can make the scale factor dimensionless by defining
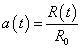
a(t) = R(t)/R0
where R0 is the current value of the scale factor. In cosmology, the subscript 0 denotes the present era. The scale factor is defined such that at the present era, it’s equal to one.
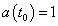
a(t0) = 1
Robertson and Walker showed that the only metric consistent with homogeneity and isotropy is
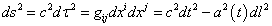
ds2 = c2 dτ2 = gij dxi dxj = c2dt2 - a2(t)dl2
where l is lower case "L", and dl depends only on spatial coordinates. Homogeneity implies that gtt = 1 giving the first “c2dt2” term. This is because all observers can agree on a single time by labeling the time according to a quantity such as density. If everyone agrees that t = 0 when ρ = 100, and t = 10 when ρ = 10, then because of homogeneity, this time will be independent of position. They will all get the same time scale if they each have a clock, and set their clocks according to the Big Bang. Since this registers proper time
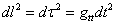
dl2 = dτ2 = gttdt2
Isotropy means there will be no cross terms such as gx. Therefore, all that is left is to write the spatial element dl.
Let's look at the case of a sphere. The surface of a sphere is two-dimensional, even though the entire sphere is three-dimensional. A sphere is a 2D space of constant radius of curvature Rc, embedded in 3D Euclidean space, and has a line element of the form
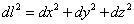
dl2 = dx2 + dy2 + dx2
and in addition, you have the restriction that
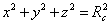
x2 + y2 + z2 = Rc2
Next switch to cylindrical polar coordinates (r, θ, z)
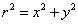
r2 = x2 + z2
then the line element is
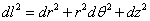
dl2 = dr2 + r2 dθ2 + dz2
You also have the restriction that
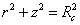
r2 + z2 = Rc2
which upon differentiating gives
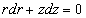
rdr + zdz = 0
You can then get rid of the dz by differentiating using
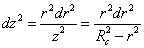
dz2 = (r2dr2)/z2 = (r2dr2)/(Rc2 - r2)
Therefore you have
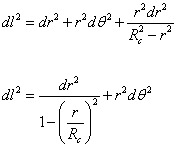
dl2 = dr2 + r2dθ2 + (r2dr2)/(Rc2 - r2)
dl2 = dr2/(1 – (r/Rc)2) + r2dθ2
You can then make the following transformation.
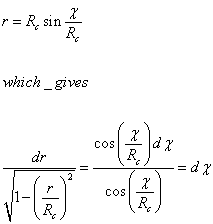
r = Rc sin X/Rc
which gives
dr/[squareroot of (1 - (r/Rc)2)] = (cos (X/Rc)dX)/(cos (X/Rc)) = dX
That is for a sphere with a 2D surface. Now, you simply do the exact same thing for a hypersphere with a 3D surface. In Euclidean 4D space, the line elements is
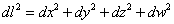
dl2 = dx2 + dy2 + dz2 + dw
with the following restriction
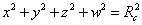
x2 + y2 + z2 = Rc2
Then you have
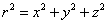
r2 = x2 + y2 + z2
The line element can be decomposed into the usual form in spherical polar coordinates (r, θ, φ) plus the new dimension.
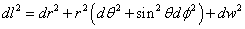
dl2 = dr2 + r2(dθ2 + sin2θdφ2) + dw2
The equation of the hypersphere becomes
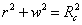
r2 + w2 = Rc2
If you differentiate the equation of the hypersphere, you get
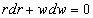
rdr + wdw = 0
and so
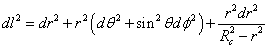
dl2 = dr2 + r2(dθ2 + sin2θ dφ2) + ((r2dr2)/(Rc2 - r2))
Thus the line element for a 3D space of constant positive curvature 1/Rc2 is given by
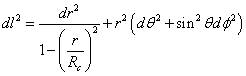
dl2 = dr2/(1 - (r/Rc)) + r2 (dθ2 + sin2 θ dφ)
Now we have dl, you can then get the metric.
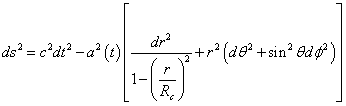
ds2 = c2dt2 - a2(t) [dr2/(1 - (r/Rc)) + r2 (dθ2 + sin2 θ dφ)]
You can define k = 1/Rc so you have
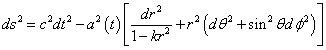
ds2 = c2dt2 - a2(t) [dr2/(1 - kr2) + r2 (dθ2 + sin2 θ dφ)]
which can also be written in the opposite sign convention, and in units where c = 1, so
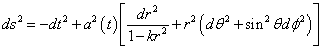
ds2 = -dt2 + a2(t) [dr2/(1 – kr2) + r2 (dθ2 + sin2 θ dφ)]
This is the Robertson-Walker metric, derived in general by H. P. Robertson in 1935, and A. G. Walker in 1936. The constant k can have values of –1, 0, or 1, which represent the following types of curvature.
k = -1 represents negative curvature, such as a saddle surface or hyperbolic geometry.
k = 0 represents zero curvature, called flat geometry.
k = + 1 represents positive curvature, such as spherical geometry.
There are many different ways of writing down the Robertson-Walker metric. Another useful form is
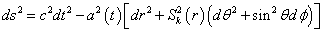
ds2 = c2dt2 - a2(t) [dr2 + Sk2(r) (dθ2 + sin2θ dφ)]
where the function Sk(r) is defined as follows.
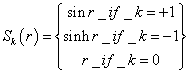
Sk(r) = sin r if k = +1
Sk(r) = sinh r if k = -1
Sk(r) = r if k = 0
You can also define the following function.
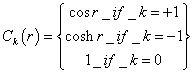
Ck(r) = cos r if k = +1
Ck(r) = cosh r if k = -1
Ck(r) = 1 if k = 0
For k = 0 and k = -1, the radial variable r can take any value from zero to infinity. However, for k = +1, r = π is the equivalent of an opposite pole of the sphere in the 2D case. Larger values of r just go around the sphere to the other side. Therefore, k = +1 is called a closed universe while k = -1 is called an open universe. Of course, k = 0 is also technically open but is called a flat universe. This just means the line element in flat. The metric is not necessarily Minkowskian.
Closed universes have finite volume, but no boundary, like the surface of a sphere. Now, we’ll show how to calculate the volume. The proper distance in the radial direction
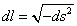
dl = [squareroot of -ds2]
with dt = 0 is
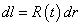
dl = R(t)dr
The form of the spherical polar angles in the metric is the same as the Euclidean, which is what you would expect since it’s isotropic. Integrating over them gives 4π steradians, so the proper volume element between shells χ to χ + Δχ is
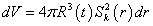
dV = 4πR3(t)Sk2(r)dr
so then the total volume is

V = 4φR3(t)[integral from 0 to rmax]Sk2(r)dr
For k = 0 or k = -1, rmax = ∞ so the volume is infinite. For k = +1, rmax = π, so you have
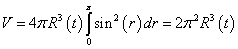
V = 4πR3(t)[integral from 0 to π]sin2(r)dr = 2π2R3(t)
which is finite. It looks like it would be possible in a closed universe to set off in one direction, fly straight without turning around, circumnavigate the universe, and eventually return to the same location from which you left. However, if you take into account the expansion of the universe, this would not be possible.
You should also not confuse the entire Universe with the observable universe, which is a sphere centered on us, with a radius of the horizon distance, which is the length that light could have traveled since the Big Bang. The observable universe is finite. The entire Universe may or may not be finite. The current evidence points to a flat universe, in which such case, it would be infinite. This also relates to common confusion regarding the Big Bang. The observable universe gets larger as time goes on, and thus began as a single point, but if the entire Universe is infinite, it was always infinite, and was not a single point at the Big Bang.
So, the following are all forms of the Robertson-Walker metric.
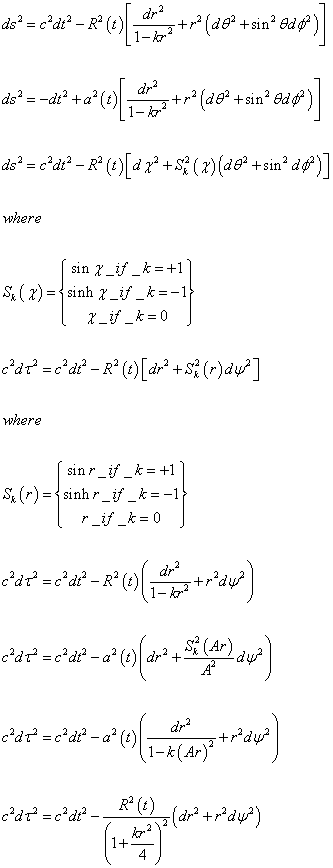
ds2 = c2dt2 - R2(t)[dr2/(1 – kr2) + r2(dθ2 + sin2θdφ2)]
ds2 = -dt2 + a2(t)[dr2/(1 – kr2) + r2(dθ2 + sin2θdφ2)]
ds2 = c2dt2 - R2(t)[dχ2 + Sk2(χ)(dθ2 + sin2θdφ2)]
where
Sk(χ) = sin χ if k = -1
Sk(χ) = sinh χ if k = -1
Sk(χ) = χ if k = 0
c2dτ2 = c2dt2 - R2(t)[dr2 + Sk2(r)dψ2]
where
Sk(r) = sin r if k = 1
Sk(r) = sinh r if k = -1
Sk(r) = r if k = 0
c2dτ2 = c2dt2 - R2(t)(dr2/(1 - kr2) + r2dψ2)
c2dτ2 = c2dt2 - a2(t)(dr2 + ((Sk2(Ar))/A2)dψ2)
c2dτ2 = c2dt2 - a2(t)((dr2/(1 – k(Ar))2) + r2dψ2)
c2dτ2 = c2dt2 - ((R2(t))/(1 + (kr2)/4)2)(dr2 + r2dψ2)
where A is a constant of proportionality which is equal to R0, which is equal to the current value of R(t). The last one is called the isotropic form. Also, with any of these, you can define the conformal time in order to take R2 out of the metric.
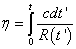
η = [integral from 0 to t]cdt'/R(t')
In my paper on tensors, I define the Christoffel symbols, Ricci tensor, and curvature scalar. I now define these quantities for the Robertson-Walker metric. Overdots represent derivatives with respect to time. The Christoffel symbols are given by
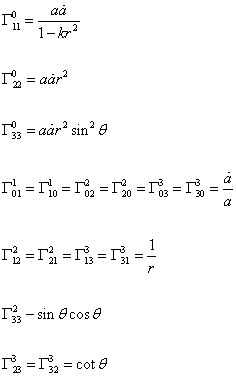
Γ110 = a[a dot]/(1 - kr2)
Γ220 = a[a dot]r2
Γ330 = a[a dot]r2sin2θ
Γ011 = Γ101 = Γ022 = Γ202 = Γ033 = Γ303 = [a dot]/a
Γ221 = -r(1 - kr2)
Γ331 = -r(1 - kr2)sin2θ
Γ122 = Γ212 = Γ132 = Γ313 = 1/r
Γ322 = -sin θcosθ
Γ233 = Γ323 = cot θ
The non-zero components of the Ricci tensor are
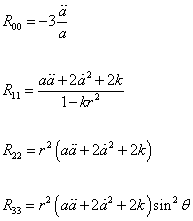
R00 = -3[a double dot]/a
R11 = (a[a double dot] + 2[a dot]2 + 2k)/(1 - kr2)
R22 = r2(a[a double dot] + 2[a dot]2 + 2k)
R33 = r2(a[a double dot] + 2[a dot]2 + 2k)sin2θ
And the curvature scalar is
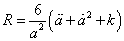
R = (6/a2)(a[a double dot] + [a dot]2 + k)
The energy-momentum tensor of a perfect fluid is
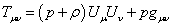
Tuv = (p + [rho])UuUv + pguv
Where [rho] is density, p is pressure as measured in the rest frame, and Uu is the four-velocity of the fluid. Perfect fluids are isotropic in their rest frame. If a fluid is isotropic in some frame, and leads to a metric that is isotropic in some frame, the two frames will coincide, and the fluid will be at rest in comoving coordinates. The four velocity is then
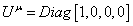
Uu = Diag[1, 0, 0, 0]
And the energy momentum tensor is
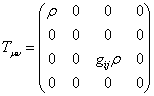
which then becomes
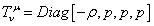
Tvu = Diag[-[rho], p, p, p]
The trace is given by
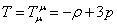
T = Tuu = -[rho] + 3p
The following is the conservation of energy equation
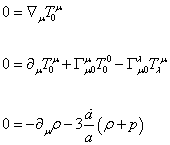
0 = [nabla]uT0u
0 = [partial derivative]uT0u + &Gammau0uT00 - Γu0λ
0 = -[partial derivative]0[rho] – 3([a dot]/a)([rho] + p)
The following is the equation of state
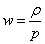
w = [rho]/p
The conservation of energy equation becomes
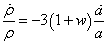
[rho dot]/[rho] = -3(1 + w)([a dot]/a)
which can be integrated to get
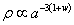
[rho] is proportional to a-3(1 + w)
There are three main things in the Universe, which are matter, radiation, and vacuum, which have the following equations of state.
Matter - w = 0
Radiation - w = 1/3
Vacuum - w = -1
Matter is nonrelativistic massive particles for which the pressure is negligible, such as stars and galaxies. Radiation includes both massless particles and massive particles moving relativistically.
The energy density of matter falls off as
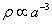
p proportional to a-3
This is the decrease in the number density of particles as the universe expands. The energy-momentum tensor of electromagnetic radiation is
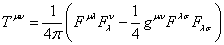
Tμν = -(1/4π)(FμλFλν - (1/4)gμνFλσFλσ
The trace of this is given by
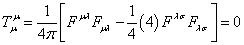
Tμμ = 1/(4π)[FμλFμλ - (1/4)(4)FλσFλσ] = 0
This has to be equal to the energy-momentum tensor of a perfect fluid.
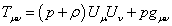
Tuv = (p + [rho])UuUv + pguv
So therefore, the equation of state is
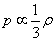
p = (1/3)[rho]
The energy density in radiation falls off as
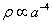
p proportional to a-4
The energy density of radiation falls off faster than that of matter because not only does the density of photons decrease but also the individual photons loose energy as 1/a as they redshift.
The Einstein equation with a cosmological constant is
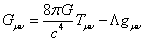
Guv = (8πG/c4)Tuv - Λguv
and if you get Tμν on one side, you have
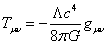
Tμν = -(Λc4/8πG)gμν
This has the form of a perfect fluid with
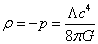
ρ = -p = Λc4/8πG
so therefore, you have w = -1, and the energy density is independent of a, which is what you would expect since the density of the vacuum is always the same. As the universe expands, energy in radiation decreases fastest, energy is matter decreases second fastest, and energy in vacuum does not decrease. Therefore, if you have a nonzero positive cosmological constant, as the universe expands, the universe will begin as radiation-dominated, pass through a matter-dominated stage, and end up as vacuum-dominated. The non-zero vacuum energy tends to win out over the long term, as long as the universe keeps expanding. Today, the contribution to the energy density of the Universe is about 0.3 matter, 0.7 vacuum, and 10-6 radiation. It’s a puzzle why the contribution from matter and the contribution from the vacuum are within an order of magnitude. Throughout most of the history of the Universe, both past and future, they will not be so close. The Universe was radiation-dominated until about 10,000 years after the Big Bang, and then was matter-dominated until recently when it started going through a transition from matter-dominated to vacuum-dominated.
Now take the energy-momentum tensor and decompose it. The μν = 0 equation is
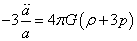
-3([a double dot]/a) = 4πG(ρ + 3p)
Due to isotropy, there is only one distinct μν = ij equation, which is
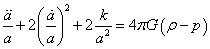
([a double dot]/a) + 2([a dot]/a)2 + 2(k/a2) = 4πG(ρ + p)
Take the first of the above two equations, and eliminate the second derivatives in the second one, and you end up with
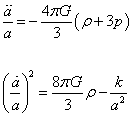
[a double dot]/a = -4πG/3 (ρ + 3p)
([a dot]/a)2 = (8πG/3)ρ - (k/a2)
There are called the Friedman equations. Robertson-Walker universes that obey the Friedman equations are called Friedman-Robertson-Walker universes. These models were first studied in 1922 and 1924 by Alexander Friedman, and independently by Georges Lamaitre in 1927. Alexander Aleksandrovich Friedman (1885 - 1925) lived in St. Petersberg, later Leningrad. Since he spelled his name in Cyrillic, there are different ways to transliterate it into English, so you see it spelled Fridman, Friedmann, Friedman, or Freedman.
Remember Hubble's Law is v = Hd, where Hubble's constant, more accurately called Hubble's parameter since it does vary, is given by
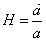
H = [a dot]/a
In other words, you could think of it as the rate that two galaxies are moving apart divided by the distance between them. The current value of the Hubble's parameter is called Hubble's constant, H0. Based on WMAP data, the current best guess for the value of the Hubble constant is 0.72 ± 0.5 or 72 km/sec/Mpc, where Mpc is megaparsec, and is equal to 3 x 1024 cm.
The following is the deceleration parameter which measures the rate of change in the rate of expansion.
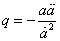
q = -(a[a double dot]/[a dot]2)
One of the most commonly used quantities in cosmology is the density parameter.
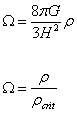
Ω = (8πG/3H2)ρ
Ω = ρ/ρcrit
where the critical density is defined as
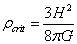
ρcrit = 3H2/8πG
You can then define the following density parameters in terms of their fraction of the critical density.
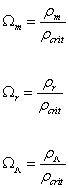
Ωm = ρm/ρcrit
Ωr = ρr/ρcrit
ΩΛ = ρΛ/ρcrit
where
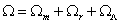
Ω = Ωm + Ωr + ΩΛ
The matter density can be further decomposed into baryonic and dark matter
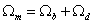
Ωm = Ωb + Ωd
The current values, based partly on WMAP data are
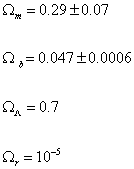
Ωm = 0.29 ± 0.07
Ωb = 0.047 ± 0.0006
ΩΛ = 0.7
Ωr = 10-6
so you have about
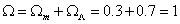
Ω = Ωm + ΩΛ = 0.3 + 0.7 = 1
The density parameters are
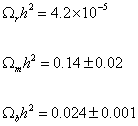
Ωmh2 = 0.14 ± 0.02
Ωbh2 = 0.02 ± 0.0001
Ωrh2 = 4.2 x 10-5
The Friedman equation says
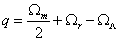
q = Ωm/2 + Ωr - ΩΛ
where q is the deceleration parameter, so therefore
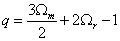
q = 3Ωm/2 + 2Ωr - 1
for a flat universe, which could be tested experimentally.
You can use the density parameter to rewrite the Friedman equation.
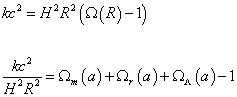
kc2 = H2 R2 (Ω(R) – 1)
kc2/(H2R2) = Ωm(a) + Ωr(a) + ΩΛ(a) – 1
In general relativity, the true source of gravity is not just mass but
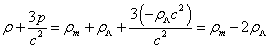
ρ + 3p/c = ρm + ρΛ + 3(-ρΛc2)/c2 = ρm - 2ρΛ
The negative pressure of the cosmological constant counter balances the gravitational attraction. The present value of the scale factor can be read from the Friedman equation.
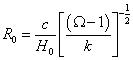
R0 = (c/H0)[(Ω - 1)/k]- ½
The Hubble constant sets the curvature length, which becomes infinitely large as Ω approaches unity from either direction. Only in the limit of zero density, does the curvature length equal the Hubble length, c/H0.
Let’s look at the following equation.
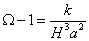
Ω - 1 = k/H2a2
If Ω is more than one, then k is positive, and the universe is closed. If Ω is less than one, then k is negative, and the universe is open. If Ω = 1, then k = 0, and the universe is flat. Then you have
| Critical Density | Density Parameter | k | Curvature |
| ρ < ρcrit | Ω < 1 | k = -1 | open |
| ρ = ρcrit | Ω = 1 | k = 0 | flat |
| ρ > ρcrit | Ω > 1 | k = +1 | closed |
It is possible to solve the Friedman equations exactly in simple cases, but it's more revealing to study its qualitative behavior. Let's say you have no cosmological constant, and you study universes with positive energy and non-negative pressure.
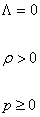
Λ = 0
[rho] > 0
p ≥ 0
Then from
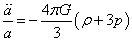
[a double dot]/a = (4πG/3)([rho] + 3p)
The deceleration parameter is always positive. If in this example, the universe can only decelerate, then it would have to be accelerating faster in the past, and if you extrapolate backwards, the universe began in a singularity called the Big Bang. We know that in reality, we have a nonzero positive cosmological constant, and the expansion is accelerating, but it still had to have begun in a Big Bang.