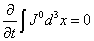
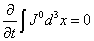
[partial derivative with respect to t][integral]J0d3x = 0
The charge is
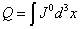
Q = [integral]J0d3x
and does not change with time.
Whenever there is a conserved current, there is a conserved charge, and vice versa. Whenever there is an invariance of the theory under some transformation, a conserved current arises, and can be written in terms of appropriate derivatives of the Lagrangian. Thus, whenever there is an invariance, there is a current, and thus a charge, although it might not be what we normally think of as a charge, but some conserved quantity. This is called Noether's Theorem. It was actually devised by a woman named Emmy Noether (1882 - 1935).
Noether's theorem says when a conserved quantity exists and how to define it. If there is a conserved quantity, there must exist an associated invariance under a transformation, in other words, a symmetry. If there is a symmetry, there must be a conserved quantity. If you are trying to write the Lagrangian, knowing the symmetries to build into the Lagrangian is a great help in writing it. Thus Noether's theorem plays a central role in relating observed symmetries and conservation laws to the structure of the theory.
Particle physics is formulated by giving the Lagrangian. From it, using the rules of quantum field theory, all aspects of particle physics can be calculated. The Lagrangian defines the theory. It is written in terms of the elementary particles of the theory. Any composite objects should appear as bound states that arise as solutions of the theory. For electromagnetism, the photon is the quantum of the electromagnetic field. It is represented by the vector potential Au. The electron is represented by the fermion field ψ. The Lagrangian contains the fundamental interactions of the theory. For electromagnetism, the interaction Hamiltonian is J . A. The relativistic expression is JuAu. Actually, it is the potential energy part of the Lagrangian that specifies the theory. The kinetic energy part depends only on the spin of the particles. The potential energy part specifies the forces and is called the interaction Lagrangian. One of the main reasons why particle physics is formulated in terms of the Lagrangian is because L is a single function that determines the dynamics, and L must be a scalar in every relevant space. L is invariant since the action is invariant. Making L invariant under Lorentz transformations means that all predictions of the theory are also Lorentz invariant.
I have described the Lagrangian for an electromagnetic field. Often however, you use a much simpler Lagrangian of a scalar field. This is the spinless field φ(x). The field φ(x) can be thought of as arising from a source the same way as the electromagnetic field arises from charged particles. Like electromagnetism, you can talk about the fields without concerning yourself with the source. Let’s say you want to write the Lagrangian analogous to the one for electromagnetism, for a real scalar field φ(x) with mass m. We derive the Lagrangian like we did before. We assume L depends explicitly on the fields and their derivatives but not on xu. L = ([phi], [partial derivative]u[phi]).

You begin with a small variation in φ(x).
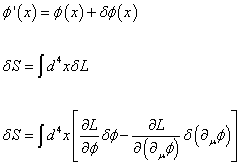
[phi]’(x) = [phi](x) + [delta][phi](x)
[delta]S = [integral]d4x[delta]L
[delta]S = [integral]d4x[[partial derivative of L with respect to phi][delta][phi] - [partial derivative of L with respect to [partial derivativeuphi][delta] ([partial derivative]uphi)]
Using
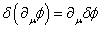
[delta]([partial derivative]u[phi]) = [partial derivative]u[delta][phi]
and integrating by parts gives
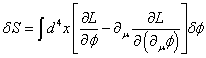
[delta]S = [integral]d4x[[partial derivative of L with respect to phi] - [partial derivative]u[partial derivative of L with respect to [partial derivative]([partial derivative]u[phi])]]
The condition for the action to be stationary (δS = 0) is
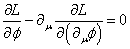
[partial derivative of L with respect to phi] - [partial derivative]u[partial derivative of L with respect to [partial derivative]([partial derivative]u[phi])] = 0
This is the Euler-Lagrange equation for φ. A real scalar field has the Lagrangian
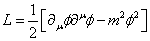
L = (1/2)[[partial derivative]u[phi][partial derivative]u[phi] - m2[phi]2]
The factor 1/2 is a convention.
The Euler-Lagrange equation gives the wave equation or Klein-Gordon equation
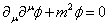
[partial derivative]u[partial derivative]u[phi] + m2[phi] = 0
That is what you would expect since
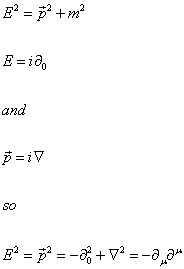
E2 = p2 + m2
E = i[partial derivative]0 and p = i[del] so
E2 - p2 = -[partial derivative]02 + [del]2 = -[partial derivative]u[partial derivative]2
Therefore every field that describes a particle of mass m should satisfy
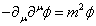
-[partial derivative]u[partial derivative]u[phi] = m2[phi]
Here is the Lagrangian
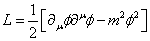
L = (1/2)[[partial derivative]u[phi][partial derivative]u[phi] - m2[phi]2]
The first term is the kinetic energy term since it arises from p2.The second term is called the mass term since it’s proportional to m2. In this case, there is no potential term, or interaction Lagrangian, since it describes a non-interacting field.
Some people say that what I’ve been calling the Lagrangian L, is actually the Lagrangian density, and the true Lagrangian is
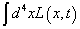
[integral]d4L(x, t)
However, most people just call L(x, t) the Lagrangian.
Let’s say you have a field normalized to a single quantum of energy w, and momentum k. If w2 = k2 + m2, then a solution to the wavefunction is
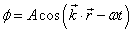
[phi] = A cos (k . r - wt)
The Hamiltonian is
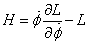
H = [phi dot][partial derivative of L with respect to phi dot] - L
so
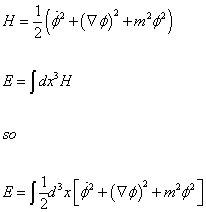
H = (1/2)([phi dot]2 + ([del][phi}2 + m2[phi]2)
E = [integral]dx3H so
E = [integral](1/2)d3x[[phi dot]2 + ([del][phi}2 + m2[phi]2]
We know that E = [h bar]w for a single quantum of energy. We’ll use natural units so [h bar] = 1. We can solve for A, and then plug it into the original equation for φ.
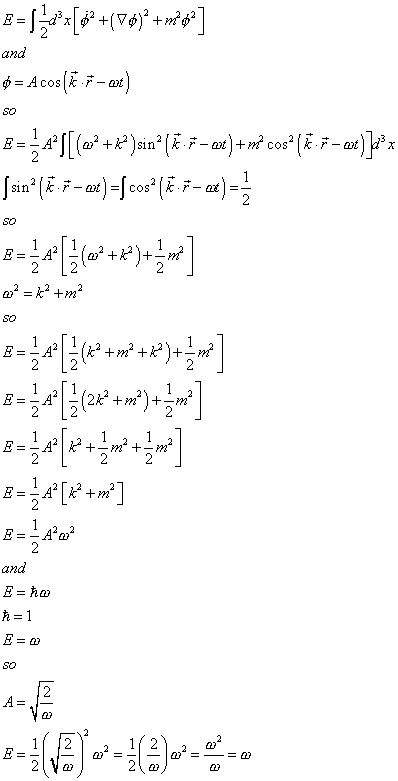
E = [integral](1/2)d3x[[phi dot]2 + ([del][phi}2 + m2[phi]2]
since [phi] = A cos (k . r - wt)
E = (1/2) A2[integral](w2 + k2) sin2 (k . r - wt) + m2cos2 (k . r - wt)]d3x
[integral]sin2(k . r - wt) = [integral]cos2(k . r - wt) = 1/2 so
E = (1/2) A2 [(1/2) (w2 + k2) + (1/2)m2]
w2 + k2 + m2 so
E = (1/2)A2[(1/2)(k2 + m2 + k2) + (1/2)m2]
E = (1/2)A2[(1/2)(2k2 + m2) + (1/2)m2]
E = (1/2)A2[k2 + (1/2)m2 + (1/2)m2]
E = (1/2)A2[k2 + m2]
E = (1/2)A2w2
since E = [h bar]w, so with [h bar]= 1, then E = w, which means A = [squareroot of](2/w)
E = (1/2)([squareroot of](2/w)]2w2 = (1/2)(2/w)w2 = w2/w = w
so A = [squareroot of](2/w) so putting that in the original equation
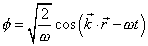
[phi] = [squareroot of 2/w] cos (k . r - wt)
One definition of the cosine function is
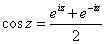
cos z = (1/2)(eiz + e-iz)
Also, the hyperbolic cosine is defined by
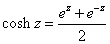
cosh z = (1/2)(ez + e-z)
The sine function is defined by
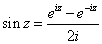
sin z = (1/2i)(eiz - e-iz)
Anyway so
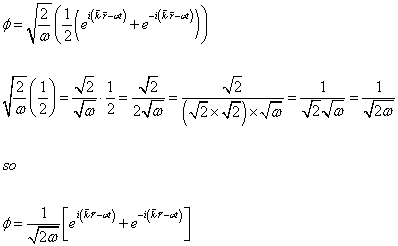
[phi] = [squareroot of 2/w]((1/2)(ei(k . r - wt) + e-i(k . r - wt)))
[squareroot of 2/w](1/2) = [squareroot of 2]/[squareroot of 2] x 1/2 = [squareroot of 2]/2[squareroot of w] = [squareroot of 2]/(squareroot of 2)(squareroot of 2)(squareroot of w) = 1/(squareroot of 2)(squareroot of w) = 1/[squareroot of 2w] so
[phi] = 1/[squareroot of 2w][ ei(k . r - wt) + e-i(k . r - wt)]
In a quantized theory, we want to speak of the creation and destruction of particles. If nk> is a state with n particles, all of the same momentum k and energy w at time t, you have
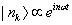
|nk> is proportional to einwt
Then a state with one less particle will be
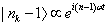
|nk - 1> is proportional to ei(n-1)wt
You would then expect the operator a that creates or destroys quanta to be a multiple of ei(n-1)wti(k . r - wt). We define a† as the operator that creates quanta associated with the field φ and a destroys them.
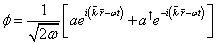
[phi] = 1/[squareroot of 2w][ aei(k . r - wt) + [a dagger]e-i(k . r - wt)]
So far we’ve discussed only free fields without considering their source or how they interact. Here is the Lagrangian of a scalar field.
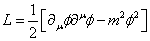
L = (1/2)[[partial derivative]u[phi][partial derivative]u[phi] - m2[phi]2]
Let’s say you add to it a part describing interactions, such as
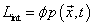
Lint = [phi]p(x, t)
Then the wave equation
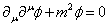
[partial derivative]u[partial derivative]u[phi] + m2[phi] = 0
then has a source term
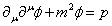
[partial derivative]u[partial derivative]u[phi] + m2[phi] = p
In terms of the analogy with electromagnetism, you can think of p as a source of the field φ. Let’s say you have the simple case.
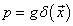
p = g[delta](x)
Here you have a time independent point source at the origin of strength g. Then you can solve the problem by using a Fourier transform.
Since p is not time dependent, you have
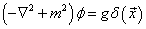
(-[del]2 + m2)[phi] = g[delta](x)
Here you have
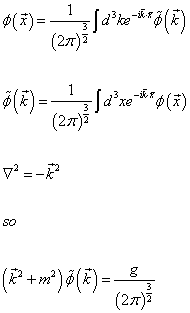
[phi](x) = (1/(2[pi])3/2))[integral]d3keik . x[phi tilde](k)
[phi tilde](k) = (1/(2[pi])3/2))[integral]d3xe-ik . x[phi](x)
[del]2 = -k2 so
(k2 + m2)[phi tilde](k) = g/(2[pi])3/2
You can then divide to get [φ tilde] and substitute back into the original equation to get φ.
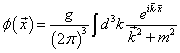
[phi](x) = g/(2[pi])3[integral]d3k (eik . x)/(k2 + m2)
If we had not taken a time independent source, the denominator would have been -k02 + k2 + m2 - k2, where k2 = kuku. The denominator is the propagator whenever a particle is exchanged in the interaction.
Putting k . x = k r cos θ you have
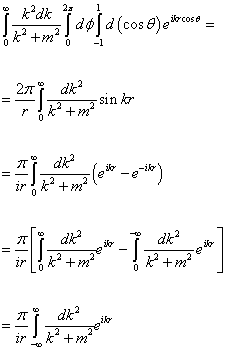
[integral from 0 to infinity]k2dk/k2 + m2 [integral from 0 to 2 pi]d[phi] [integral from -1 to 1] d(cos [theta])eikr cos [theta] =
= 2[pi]/r [integral from 0 to infinity] (dk2/k2 + m2) sin kr
= [pi]/ir [integral from 0 to infinity] (dk2/k2 + m2) (eikr - e-kr)
= [pi]/ir [[integral from 0 to infinity] (dk2/k2 + m2) (eikr) - [integral from 0 to minus infinity] (dk2/k2 + m2) (eikr)]
= [pi]/ir [integral from minus infinity to infinity] (dk2/k2 + m2) (eikr)
This can be evaluated as a contour integral. Closing the contour where Im k > 0 so the integral is convergent, and picking up a contribution from the residue at k = im, gives finally
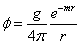
[phi] = (g/4[pi]) (e-mr/r)
Hideki Yukawa (1907 - 1981) identified φ as a meson field with the nucleon as a source, analogous to how any charged particle is the source of an electromagnetic field. Just as the effects of the electromagnetic field are transmitted by photons, the effects of the meson field should be transmitted by mesons. When the particles have a mass m, the field is significant in size only out to a range of force r ~ 1/m.
Now we want to extend this to see how one nucleon would interact with another by sensing its meson field. The interaction Hamiltonian between two nucleons, the second one described by p2(x), is
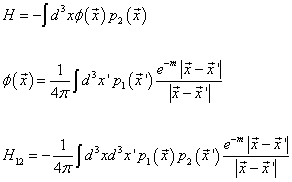
H = -[integral]d3x[phi](x) p2(x)
[phi](x) = (1/4[pi]) [integral]d3x’ p1(x’) ((e-m|x - x’|)/(|x - x’|))
H12 = -(1/4[pi]) [integral]d3x d3x’ p1((x) p2((x’)((e-m|x - x’|)/(|x - x’|))
Therefore the potential can be written as
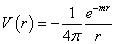
V(r) = -(1/4[pi]) (e-mr/r)
Notice that since photons are massless, in that case, the equation reduces to the familiar case from electrostatics.
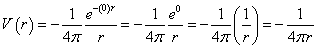
V(r) = -(1/4[pi]) (e-(0)r/r) = -(1/4[pi]) (e0/r) = -(1/4[pi]) (1/r) = -1/4[pi]r
This result leads to the general interpretation in quantum field theory that all interactions are due to the exchange of field quanta. Force and interaction become interchangeable. The equation for H12 gives the interaction in position space. Usually, you write matrix elements in momentum space. The momentum space quantity representing the exchanged particle of mass m is
1/(k2 - m2)
This is called the propagator. The complete propagator also has a phase factor and a numerator that depends on the spin of the exchanged particle.
Here are some Lagrangians used in particle physics.
Real spin-zero field of mass m (scalar or pseudoscalar)
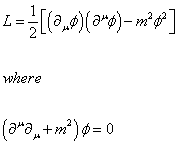
L = (1/2) [([partial derivative]u [phi])( [partial derivative]u [phi]) - m2 [phi]2]
where ([partial derivative]u[partial derivative]u + m2)[phi] = 0
Complex scalar or psuedoscalar field of mass m, or two real scalars of the same mass
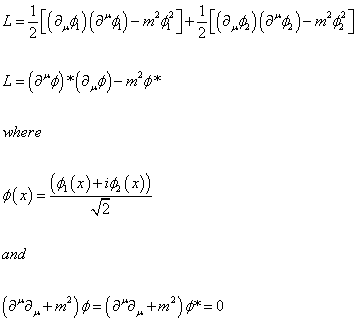
L = (1/2) [([partial derivative]u [phi]1)( [partial derivative]u [phi]1) - m2 [phi]12] + (1/2) [([partial derivative]u [phi]2)( [partial derivative]u [phi]2) - m2 [phi]22]
L = ( [partial derivative]u [phi])* )( [partial derivative]u [phi]) - m2[phi]*
where [phi](x) = ([phi]1(x) + i[phi}2(x))/[squareroot of 2]
and ([partial derivative}u [partial derivative}u + m2)[phi] = ([partial derivative}u [partial derivative}u + m2)[phi]* = 0
Spin - 1/2 fermion field of mass m
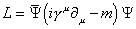
L = [psi bar](i[gamma]u[partial derivative]u - m)[psi]
where ψ satisfies the Dirac equation
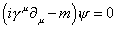
(i[gamma]u[partial derivative]u - m)[psi] = 0
Massive Abelian vector field
If there were an Abelian field Bu, like the electromagnetic field except massive, the following term is added to the Lagrangian
(1/2)m2BuBu
If you see the term BuBu, it’s coefficient is (mass)2
Non-Abelian vector field
There are non-Abelian gauge fields such as the gluon or W fields. The vector potential Au of electromagnetism is generalized to a non-Abelian field that has an internal index a so that the non-Abelian vector potential can be written as Wau. For SU(2), a = 1, 2, 3. For SU(3), a = 1, 2, 3, ...8. Then we define
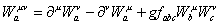
Wauv = [partial derivative]u Wa v - [partial derivative]v Wa u + gfabc Wbu Wcv
The fabc are structure constants. For SU(2), fabc = εabc. The extra term is necessary to the make the vector, in internal space, transform correctly under rotations. The form of Wauv is gauge invariant.
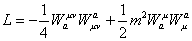
L = -(1/4) Wauv Wuva + (1/2)m2 Wau Wua
Electromagnetism
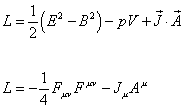
L = (1/2)(E2 - B2) - pV + J . A
L = -(1/4)FuvFuv - JuAu
Quantum Chromodynamics
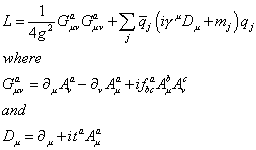
L = (1/4g2)Guva Guva + [summation of j][q bar]j(i[gamma]uDu + mj)qj
where Guva = [partial derivative]uAva - [partial derivative]vAua + ifbca Aub Avc
and Du = [partial derivative]u + it Aua
Here mj and qj are the mass and quantum field of the quark of jth flavor. A is the gluon field with spacetime indices u and v, and color indices a, b, and c. The numerical coefficients f and t guarantee SU(3) symmetry. The quark masses and coupling constant g are free parameters.
The Yang-Mills equations are four dimensional equations for the gluon fields in strong interactions, meaning quantum chromodynamics. In a formalism where time is imaginary, which is Euclidean space, these equations have a soliton-like solution called the instanton. The instanton is a solution of the classical Yang-Mills equations in Euclidean space. It is the basis of a lot of semiclassical calculations which are based on classical solutions. The main property of instantons is that they carry the topology of the vacuum.