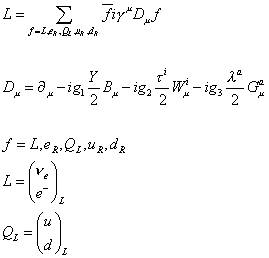
This paper is written for a general audience although I admit there are parts which the average person would not understand, which they can safetly skip over. For a more technical treatment, read my papers on tensors, Lagrangians, the Standard Model, and beyond the Standard Model. Some writers use the phrase "particle physics" to specifically refer to the physics of the 1960's and 1970's. Other people simply use it to mean the study of our Universe at the smallest scale. Probably the first scientist was Thales of Miletus (620 B.C. - 546 B.C.) who claimed that the fundamental element was water. Anaximenes claimed it was air. Empedocles (495 B.C. - 435 B.C.) was one of the first to suggest that the world was made of the four elements of fire, earth, air, and water. The proportions with which they were combined determined the properties of the material. Anaxagoras claimed there was an infinite number of elements. In Plato’s "Timaeus", he suggested that at very small distance scales, the four elements, fire, earth, air, and water, were composed of miniature polyhedra. Fire was associated with the tetrahedron, earth with the cube, air with the octahedron, and water with the icosahedron. There was one platonic solid, the dodecahedron, left over, so he suggested that it composed some otherworldly substance that the celestial objects were made out of. The twelve faces of the dodecahedron corresponded to the twelve signs of the Zodiac. Since three of the five solids had triangles for faces, those could come apart and reassemble into each other, in almost a type of nuclear reaction where you have a transmutation of the elements. Leucippus, Democritus and others theorized that matter was made of atoms, but the overwhelming view was that matter was composed of the four elements of fire, earth, air, and water. In medieval and Renaissance Europe, there was a shift to viewing what chemists now call the elements to be fundamental. They hoped that gold was not one of these fundamental elements and thus could be created by a chemical reaction. Although that was misguided, in the process, they created the field of chemistry. Dmitri Mendeléev (1834 - 1907) was a Russian chemist who arranged the 63 known elements into a periodic table based on atomic mass, which he published in "Principles of Chemistry" in 1869. In the 19th Century, elements came to be considered as composed of atoms, which were indivisible, and were considered the smallest possible things. The primary motivation for this general acceptance of atoms was to explain why chemical reactions used up reactants in precise proportions, as well as the compressibility of gases. In 1897, J.J. Thompson discovered the electron which he called "corpusles", and were smaller than atoms.
Throughout most of history, there was a debate as to whether light is a wave or a particle. Isaac Newton thought that it was a particle. Most people bowed to the opinion of this great man. In 1819, Augustin Fresnel showed that it was a wave. Fresnel was a young military engineer who followed his passion for optics largely in the spare time that he could wrench from his military duties. He wrote an essay on the subject of diffraction. Poisson pointed out that according to Fresnel's theories, a bright spot should appear in the center of a shadow of a sphere. Fresnel's bright spot, as it came to be called, was found, proving that light was a wave. Since then, there was overwhelming evidence that light was a wave, such as detailed studies of reflection, refraction, polarization, interference, and diffraction. Young's double slit experiment illustrates the wave nature of light. They could explain all of these phenomena by treating light as an electromagnetic wave governed by Maxwell's equations. The evidence for this belief was overwhelming.
The late 19th Century was one of the only times in human history in which physics could explain essentially everything that was observed. The exceptions were the photoelectric effect, the Compton Effect, blackbody radiation, and why did light appear to have the same speed for all observers. All of these were solved by Albert Einstein, the last by special relativity, the first two by saying that light could be a particle, and third one by saying that there are discrete energy levels in the atom, which is actually another way of saying that light could be a particle.
The photoelectric effect is when a beam of light strikes a metal surface, and strikes electrons from that surface. The data can be explained by saying that light was a particle. In the wave theory, the more intense the light, the more energetic would be the ejected electrons which is not the case. If you double the intensity of the light, you double the number of photons, but the energy per photon is unchanged. According to the wave theory, electrons would be ejected at any frequency if the light was intense enough. In reality, there is a cut off frequency below which there is no photoelectric effect. If the photon energy exceeds the work function of the material, hv>[phi], the photoelectric effect can occur. According to the wave view, in feeble light, there would be a time delay between the light striking the surface and the electron emerging from it. There is not because the photon energy is delivered in a single collision event. It was for his explanation of the photoelectric effect that Einstein received the Nobel Prize in physics in 1921.
In the early 19th Century, the physics community was hostile to anyone suggesting that light be viewed as a wave and not a particle. A century later, they were equally hostile to anyone suggesting that light be viewed as a particle and not a wave. One of the great convincers was the Compton Effect. If you fire x-rays at a graphite target, the incident beam has a single wavelength, but the scattered x-rays peak at two wavelengths. This can't be explained in the wave view. In the particle view, some of the photons make billiard ball like collisions with individual free electrons in the target. The electron picks up kinetic energy from the encounter, and so the scattered photon will have a lower energy, and thus a longer wavelength.
The maximum energy which can be radiated by an object is called the blackbody radiation. A blackbody is a theoretical object, (i.e. emissivity = 1.0), which is both a perfect absorber and emitter of radiation. Common usage refers to a source of infrared energy as a "blackbody" when it's emissivity approaches 1.0 (usually e = 0.99 or better) and as a "graybody" if it has lower emissivity. The radiation given off by a blackbody occurs in a wide range or spectrum of wavelengths and, based on careful measurements and quantum theory, Max Planck produced an equation to model the observed blackbody radiation curve. His discovery is considered to be one of the most important in the field of quantum physics.
In the 19th Century, people could not explain the radiation emitted by hot objects. Most hot glowing things, such as a red hot poker, depend on too many variables, so they would study cavity radiation. You form a cavity within a body, the interior walls being held at a constant temperature. You drill a hole in the cavity wall so a sample of light can escape. This cavity radiation will have a very simple spectrum, determined only by the temperature of the walls. The spectral radiancy S([lambda]) is defined so that S([lambda])d[lambda] gives the radiated power per unit area of the cavity aperture that lies in the wavelength interval [lambda] to [lambda] + d[lambda]. This is the classical radiation law.
S([lambda]) = (2[pi]ckT)/[lambda]4
where c is the speed of light, c = 2.9979 x 108 m/s, and k is the Boltzmann constant, k = 1.38 x 10-23 J/K = 8.62 x 10-5 eV/K. This equation agrees with experiment at long wavelengths but disagrees at short wavelengths. This was called the ultraviolet catastrophe. In 1900, Max Planck came up with an equation that fit the experimental data perfectly for all wavelengths and temperatures.
S([lambda]) = ((2[pi]hc2)/[lambda]^5)(1/e^(hc/[lambda]kT)-1))
where h is Planck's constant, h = 6.63 x 10-34 Js. Planck found this equation, but nobody understood why it worked. Planck himself failed to see its significance. In 1917, Einstein analyzed the equation, and pointed out its underlying assumptions. The first assumption is that the energy in the cavity is quantized. The radiation exists in the form of photons with energy E = hv. The second assumption is that the energy of the atoms that form the cavity walls is quantized. The atoms that form the walls of the cavity can exist only in states of definite energy. States with intermediate energy are forbidden. This ties in with the idea that light can be a particle, since if the atom can only emit and absorb energy in the form of discrete photons, there would be energy levels in the atom.
You can learn about the detailed structure of individual atoms by studying the light they emit or absorb when they stand alone, isolated from other atoms. The light emitted by such isolated atoms occurs only in a spectrum of sharply defined wavelengths called spectral lines. Atoms of each element have different spectral lines. There are spectral lines characteristic of isolated molecules or atomic nuclei. The simplest spectrum is that of the simplest atom, hydrogen. When people try to come up with theories of the atom, they begin with hydrogen.
Democritus (460 B.C. - 370 B.C.) suggested that all things were composed of minute, invisible, indestructible particles of matter called "atoma". John Dalton (1766 - 1844) came up with a theory that matter is composed of atoms of differing weights that combine in simple ratios of weight. Atoms were imagined as tiny marbles. Ernest Rutherford (1871 - 1937) discovered the atomic nucleus. In 1911, he was firing electrons at atoms, and some of them came at him. He said it was like firing a gun at tissue paper, and the bullet ricocheting off and hitting you. This implied a nucleus of protons surrounded by electrons. However, classical physics was incapable of explaining this. Imagine that the electron in the hydrogen atom revolves about the central nucleus, a proton, in a circular orbit of radius r, similar to the Moon orbiting the Earth. The frequency of the radiation that the atom emits would be equal to the frequency at which the electron circulates in this orbit. Classical theory predicts that such an accelerating electron will indeed radiate, and at its orbital frequency. However, the orbiting electron will radiate its energy completely away, emitting a continuous spectrum of radiation as it spirals in toward the nucleus. Thus the great theories of Newton and Maxwell stand helpless before the simplest atom. They can't even account for the existence of spectral lines, let alone their wavelengths. Indeed they predict that atoms can not exist.
The idea of electrons orbiting the nucleus is so absurd. Despite this, there was an episode of Star Trek: Next Generation, in which the characters were robbed of their dreams, and Diana Troi was receiving telepathic visions of a single moon orbiting a planet. The characters, for some reason, decided that this was a reference to hydrogen. They pumped large amounts of hydrogen into the vortex, or whatever they called it, which miraculously was what the aliens wanted.
In 1913, Danish physicist Niels Bohr (1885 - 1962) proposed a model for the hydrogen atom that not only accounted for the presence of spectral lines but, with no adjustable parameters whatsoever, predicted their wavelengths to an accuracy of 0.02%. Bohr assumed that hydrogen can exist without radiating in any one of a discrete set of stationary states of fixed energy. This assumption of energy quantization flies in the face of classical theory, but Bohr's attitude was, "Let's assume it anyway and see what happens". Bohr assumed that the hydrogen atom can emit or absorb radiation only when the atom changes from one of its stationary states to another. The energy of the emitted or absorbed photon is equal to the difference in energy between the two states. Thus if an atom changes from an initial state of energy Ei to a final state lower state of energy Ef, the energy emitted by the photon is hv = Ei - Ef, a relation known as the Bohr frequency condition. Bohr found that the energies of the stationary states of the hydrogen atom are given by
E = -(me4)/(8([epsilon]2)(h2)(n2))
where n is the quantum number, and n = 1, 2, 3, etc. The lowest energy state, E1, is the ground state. E1 = -13.6 eV, so the above equation can be rewritten as E = -(13.6eV)/n2, where n = 1, 2, 3, etc.
1/[lambda] = R(1/(l2) - 1/(u2)
where u and l are the quantum numbers of the upper and lower energy states. R is the Ryberg constant, R = 0.01097 n/m.
Although Bohr's theory was successful for hydrogen, it proved less useful for more complex atoms. Bohr's approach was semiclassical and was an intermediate step in the development of a full quantum theory.
Also, Niels Bohr's son shared a Nobel Prize in physics with a guy who went to my highschool.
Light can be viewed as either a particle or a wave. How is that possible? Unfortunately, this has always been widely misunderstood. At first people would say that it went back and forth between being a particle and a wave. Then people would say that it was always a particle and wave but you couldn't see both aspects at once, like you can't see both sides of a sheet of paper at once. You can't simultaneously see its wave-like and particle-like characteristics. A more accurate way of describing it is to say that it is a subatomic entity that under some circumstances manifests itself mathematically as a particle, and under other circumstances, manifests itself mathematically as a wave. Even this though, is not entirely 100% accurate, because you are still describing it as somehow being two things. It's not two things! It's one thing! A photon is a subatomic entity totally unlike anything in the macroscopic environment. The problem people have is that they want to visualize it. They feel that in order to "know" what something is, they have to visualize it. However, when you visualize anything, what you are visualizing is something from the macroscopic environment, your daily life. Therefore, when you try to visualize a photon, you are assuming that it's analogous to something in the macroscopic environment. This is a false assumption. A photon is no way analogous to anything in the macroscopic environment. You have to ween yourself from the desire to visualize it. You have to remember that when people talk about a photon being a particle or a wave, that these are metaphors.
Of course, a photon is not the only particle that can be described as either a particle or a wave. Any particle can be described as particle or a wave. An electron could be viewed as wave, for instance. Here are relations between the momentum of a particle, when viewed as a particle, and the wavelength of the particle, when viewed as a wave: p = h/[lambda] and [lambda] = h/p. The wavelength of a particle is called the de Broglie wavelength. C. J. Davisson and L. H. Germer were the first to measure the de Broglie wavelength of electrons. With matter waves, the quantity whose variation with position and time represents the wave aspect of the particle is its wave function, and is represented by the symbol [psi], which looks like a trident. Localizing the extent of a wave in space has the result that only a discrete set of wavelengths, and correspondingly, a discrete set of frequencies can occur. That is, localization leads to quantization.
Let's say you have light bouncing back and forth between two parallel mirrors. Let's say you look at the amplitude of oscillation for the lowest frequency oscillation mode, or n = 1. It would form a parabola. Now take that parabola and square it. You end up with a bell curve. That bell curve represents the likelihood of finding a photon at any given point. The square of the amplitude of the wave is proportional at any point to the density of the photons at that point. Now you can do the same thing with an electron. Let's say you have an electron trapped in an infinite well. The potential energy is zero within the one dimensional trap and infinity at 0 and L. The probability density for the electron in its ground state, n = 1, is a bell curve. The probability of finding the electron at any given location is proportional to the square of the amplitude of the matter wave at that location. The quantity [psi]^2(x)dx is proportional to the probability of finding the electron in the interval between x and x + dx.
[integral from 0 to L] [psi]2(x)dx = 1
This is the energy of an electron trapped in an infinite well.
En = (n2)((h2)/8m(L2)) where n = 1, 2, 3, etc.
You can extend the example of an electron trapped in an infinite well to a more realistic case of an electron trapped in a hydrogen atom.
En = - ((me4)/8([epsilon]2)(h2)(n2) where n = 1, 2, 3, etc.
Here is the probability density for the ground state of a hydrogen atom.
[psi]2(r) = (e(-2r/rB))/([pi](rB3))
where rB is the Bohr radius. RB = 5.29 x 10-11 m = 52.9 pm. [psi]2(r)dV is proportional to the probability that the electron will be in any specified infinitesimal volume element dV.
It requires four quantum numbers to describe completely the quantum states of the hydrogen atom. This same set of four numbers also serves to identify the quantum states of single electrons in multi-electron atoms. The four numbers are the principal n, associated with the energy, the orbital l, associated with the orbital angular momentum, the magnetic ml, associated with the orbital angular momentum, and the spin ms, associated with the spin angular momentum.
An electron approaching a flat potential barrier of height U and thickness L has a finite probability T, the transmission coefficient, of penetrating the barrier even if its kinetic energy E is less than the height of the barrier. The probability is
T = e(-2kL) where k = squareroot of (8([pi]2)m(U-E)/h2)
For a problem in classical mechanics, you use Newton's laws. For a problem in electromagnetism, you use Maxwell's equations. For a problem in wave mechanics, you use Schrodinger's equation, which was first advanced by Austrian physicist Erwin Schrodinger in 1926.
The Heisenberg Uncertainty Principle states that you can not, even in principle, measure both a particle's position r and momentum p with arbitrary precision. The uncertainties associated with each component of r and p must obey a relationship of the following form. ([delta]x)([delta]p) = h. The principle also applies to energy and time measurements in the form ([delta]E){[delta]t) = h. Therefore over smaller and smaller intervals of time, you can borrow larger and larger amounts of energy. The vacuum is filled with particle-antiparticle pairs continually coming into existence, and annihilating, the energy for their creation coming from their annihilation. The shorter the interval of time, the shorter the distance a particle can travel in that time. Therefore over shorter and shorter distances, the more energy is available. There is energy great enough to briefly create particles that otherwise only existed shortly after the Big Bang. The world shortly after the Big Bang, in which the unification of the four forces is obvious, still exists today albeit only over very short distance scales.
In the early 20th Century, the only matter particles known to exist were the proton, neutron, and electron. Then additional particles were discovered in cosmic rays and particle accelerators. By the mid-1960s, physicists realized that their previous understanding, where all matter is composed of the fundamental proton, neutron, and electron, was insufficient to explain the myriad of new particles being discovered. Gell-Mann's and Zweig's quark theory solved these problems. Over the last thirty years, the theory that is now called the Standard Model of particles and interactions has gradually grown and gained increasing acceptance with new evidence from new particle accelerators.
In 1964, Murray Gell-Mann and George Zweig tentatively put forth the idea of quarks. They suggested that mesons and baryons are composites of three quarks or antiquarks, called up, down, or strange (u, d, s) with spin 0.5 and electric charges 2/3, - 1/3, -1/3, respectively. It turns out that this theory was not completely accurate. Since the charges had never been observed, the introduction of quarks was treated more as a mathematical explanation of flavor patterns of particle masses than as a postulate of an actual physical object. Later theoretical and experimental developments allowed us to now regard the quarks as real physical objects, even though they can not be isolated. It's sort of the opposite of "lines of force" which were originally considered physical entities but are now regarded as mathematical constructs.
Murray Gell-Mann thought up the name "quark" by taking it from a line from James Joyce's "Finnegan's Wake" where it says, "three quarks for Muster Mark." Gell-Mann said that initially he didn't know where he got the name, and then he realized where he had heard it. It seemed appropriate since at that time only three quarks, up, down, and strange, were theorized. Gell-Mann also said the line suggested to him, "three quarts for Mister Mark," implying a guy drinking at a pub. James Joyce invented the word "quark" after hearing seagulls cawing. James Joyce got the title "Finnegan's Wake" from a popular Irish folksong of the same name. Since I was little, on St. Patrick's Day, we would listen to Irish records, one of which had that song. I first heard the word "quarks" when I was in the 5th grade, watching Carl Sagan's "Cosmos." At the time, I never imagined a connection between those two things.
Since quarks and leptons had a certain pattern, several papers suggested a fourth quark carrying another flavor to give a similar repeated pattern for the quarks, now seen as the generations of matter. Very few physicists took this suggestion seriously at the time. Sheldon Glashow and James Bjorken coined the term "charm" for the fourth (c) quark. In1965, O. W. Greenberg, M. Y. Han, and Yoichiro Nambu introduce the quark property of color charge. All observed hadrons are color neutral.
In 1967 Steven Weinberg and Abdus Salam separately propose a theory that unifies electromagnetic and weak interactions into the electroweak interaction. Their theory requires the existence of a neutral, weakly interacting boson (now called the Z0) that mediates a weak interaction that had not been observed at that time. They also predict an additional massive boson called the Higgs Boson that has not yet been observed.
In 1968-69, At the Stanford Linear Accelerator, in an experiment in which electrons are scattered off protons, the electrons appeared to be bouncing off small hard cores inside the proton. This is similar to the discovery of the atomic nucleus. JamesBjorken and Richard Feynman analyzed this data in terms of a model of constituentparticles inside the proton They didn't use the name "quark" for the constituents, even though this experiment provided evidence for quarks. Sheldon Glashow, John Iliopoulos, and Luciano Maiani recognized the critical importance of a fourth type of quark in the context of the Standard Model. A fourth quark allows a theory that has flavor-changing Z0-mediated weak interactions but no flavor-changing ones. Donald Perkins, spurred by a prediction of the Standard Model, re-analyzed some old data from CERN and found indications of weak interactions with no charge exchange, those due to a Z0 exchange.
Then, quantum field theory of strong interaction was formulated. This theory ofquarks and gluons, now part of the Standard Model, is similar in structure to quantumelectrodynamics (QED), but since strong interaction deals with color charge this theory iscalled quantum chromodynamics (QCD). Quarks were determined to be real particles, carrying a color charge. Gluons are massless quanta of the strong-interaction field. This strong interaction theory was first suggested by Harald Fritzsch and Murray Gell-Mann.
In 1973, David Politzer, David Gross, and Frank Wilczek discovered that the color theory of the strong interaction has a special property, now called "asymptotic freedom." The property is necessary to describe the 1968-69 data on the substrate of the proton. In 1974, in a summary talk for a conference, John Iliopoulos presented, for the first time in a single report, the view of physics now called the Standard Model. That same year, Burton Richter and Samuel Ting, leading independent experimenters, announced on the same day that they discovered the same new particle. Ting and his collaborators at Brookhaven called this particle the "J" particle, whereas Richter and his collaborators at SLAC called this particle the psi particle. Since the discoveries are given equal weight, the particle is commonly known as the J/psi particle. The J/psi particle is a charm-anticharm meson.
In 1976, Gerson Goldhaber and Francois Pierre found the D0 meson, anti-up and charm quarks. The theoretical predictions agreed dramatically with the experimental results, offering support for the Standard Model. That same year, the tau lepton was discovered by Martin Perl and collaborators at SLAC. Since this lepton is the first recorded particle of the third generation, it was completely unexpected. In 1977, Leon Lederman and his collaborators at Fermilab discovered yet another quark and its antiquark. This quark was called the "bottom" quark. Since physicists assumed that quarks came in pairs, this discovery added impetus to search for the sixth quark, "top."
Charles Prescott and Richard Taylor observed a Z0 mediated weak interaction in the scattering of polarized electrons from deuterium which shows a violation of parity conservation, as predicted by the Standard Model, confirming the theory's prediction. The W± and Z0 intermediate bosons demanded by the electroweak theory were observed by two experiments using the CERN synchrotron using techniques developed by Carlo Rubbia and Simon Van der Meer to collide protons and antiprotons.
In 1989, experiments carried out in SLAC and CERN strongly suggested that there are three and only three generations of fundamental particles. This was inferred by showing that the Z0-boson lifetime is consistent only with the existence of exactly three very light or massless neutrinos. According to the Standard Model, there are three generations of particles, each containing two quarks, and two leptons, one of which is a neutrino. Neutrinos are very weakly interacting particles. The electron neutrino was first theorized by Wolfgang Pauli in 1931. The last neutrino to be observed, the tau neutrino, was first observed in 2000.
In 1995, after eighteen years of searching at many accelerators, the CDF and D0 experiments at Fermilab discovered the top quark at the unexpected mass of 175 GeV. No one understands why the mass is so different from the other five quarks.
In order to write down the Standard Model Lagrangian, you need the notation of the Dirac equation in order to express the spin structure, the requirements of gauge invariance that tell us to begin with a free particle Lagrangian and rewrite it with covariant derivative, and the idea of internal symmetries. In order to describe the particles and interactions known today, three internal symmetries are needed. Today, all experiments are consistent with the idea that the three symmetries are necessary and sufficient to describe the interactions of the known particles. It is easiest to describe how these symmetries act in the language of group theory.
All particles appear to have a U(1) invariance. That invariance was related to theelectromagnetic interaction. All particles appear to have a second invariance under a set of transformations that form an SU(2) group, called the electroweak SU(2) invariance. These lead to a non-Albelian gauge phase invariance, analogous to the strong isospin invariance. The associated gauge bosons necessary to maintain the invariance of the theory are called Wi. There is one boson for each of the three generators of SU(2) transformations so i = 1, 2, or 3. There is a third internal invariance, under a set of transformations that form an SU(3) group, giving an additional independent non-Albelian invariance. The associated gauge bosons are labeled Ga, where a = 1, 2, ... 8 since there is one spin-one boson for each of the eight generators of SU(3). The bosons are called gluons, and theory of particle interactions via gluon exchange is called Quantum Chromodynamics (QCD).
Here is the Standard Model Lagrangian.
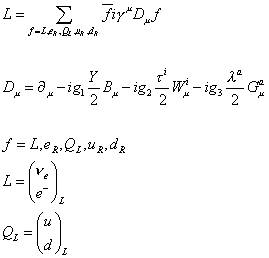
Lferm = [summation] [f bar]i ([gamma]u)(Du)f
Du = [partial derivative of u] - ig1(Y/2)Bu - ig2(([tau]i)/2)(Wui) -ig3(([lambda]i)/2)Gua
L = [summation, f = L, eR, QL, uR, dR] [f bar] i[gamma]u Du f
where Du = [partial derivative]u - ig1(Y/2)Bu - ig2([tau]i/2)Wui - ig3([lambda]a/2)Gua
f = L, eR, QL, uR, dR
L = ([nu]e e)L QL = (u, d)L
and where Y is the hypercharge, [tau]i are the Pauli spin matrices, [lambda]a are the Gell-Mann matrices, and g1, g2, and g3 are coupling constants.
There are six color charges. They are red, blue, green, antired, antiblue, and antigreen. The six quarks, six antiquarks, and gluons have color charge. Particles with color charge can only combine is ways which cause the colors to cancel out. Currently, there are fourknown ways this can happen.
Three quarks = red, blue, green = baryon
Three antiquarks = antired, antiblue, antigreen = antibaryon
Quark-antiquark pairs = red-antired, blue-antiblue, or green-antigreen = meson
gluon-antigluon pairs = red-antired, blue-antiblue, or green-antigreen = glueball
If you had two red quarks, two blue quarks, and two green quarks, the color charges would also cancel, but that would be two baryons. It has been suggested that there could possibly exist other combinations of various numbers of quarks, antiquarks, and gluons but that's tentative conjecture.
Here are some baryons. The antibaryons of these would be the same except the particlesand antiparticles would be reversed.
proton = two up quarks and a down quark = uud
neutron = two down quarks and an up quark = udd
lamda = an up quark, down quark, and strange quark = uds
sigma+ = uus
sigma- = dds
sigma0 = uds
xi+ = uss
xi- = dss
Here are some mesons.
pion+ = an up quark and an down antiquark = u[d bar]
pion- = an up antiquark and a down quark = [u bar]d
K+ = u[s bar]
K- = [u bar]s
K0 = d[s bar]
[K0 bar] = [d bar]s
According to the Standard Model, there are three generations of fermions, each containing two quarks, and two leptons. The first generation is the up quark, down quark, electron and electron neutrino. The second generation is the strange quark, charm quark, muon and muon neutrino. The third generation is the top quark, bottom quark, tau particle, and tau neutrino. The fundamental bosons are the photon, the eight gluons, the W+, W-, and Z0 vector bosons, and the graviton. What you think of as "normal matter" is composed of up quarks, down quarks, and electrons.
A problem with the Standard Model is the question of why is it that the W+, W-, and Z0 particles that mediate the weak force have mass, while the other force carriers, the photon, eight gluons, and graviton, are massless. A new ingredient for the formulation of gauge theories was introduced by F. Englert and Robert H. Brout of the University of Brussels, and by Peter Higgs of the University of Edinburgh. They found a way to endow some of the Yang-Mills fields with mass while retaining exact gauge symmetry. This technique is now called the Higgs Mechanism.
The fundamental idea of the Higgs Mechanism is to include in the theory an extra field, one having the unusual property that it does not vanish in the vacuum. You usually think of vacuum as space with nothing in it, but in physics, vacuum is defined as the state in which all fields have their lowest possible energy. For most fields, the energy is minimized when the value of the field is zero everywhere. An electron field, for instance, has its minimum energy when there are no electrons. The Higgs field is unusual in this respect. Reducing it to zero costs energy. The energy of the field is smallest when the field has some uniform value greater than zero. Therefore, Higgs particles will exist in any vacuum.
The effect of the Higgs field is to provide a frame of reference in which the orientation of the isotropic arrow can be determined. The Higgs field can be represented as an arrow superimposed on the other isotropic indicators in the imaginary internal space of the hadron. What distinguishes the arrow of the Higgs field is that it has a fixed length, established by the vacuum of the field. The orientation of the other isotropic spin arrows can then be measured with respect to the axis defined by the Higgs field. In this way, a proton can be distinguished from a neutron.
Before symmetry breaking, you have two neutral Higgs particles (H0), one negative Higgs particle (H-), and one positive Higgs particle (H+). After symmetry breaking, you have one neutral Higgs particle, H0, and the three intermediate vector bosons: W+, W-, and Z0.
What is called the Higgs Mechanism is the extension of the spontaneous symmetry breaking to create massive vector bosons in a gauge invariant theory. Here it will be shown for a U(1) theory.
Du = + iqAu
Adding the Lagrangian of the free gauge field A results in
L = Du[phi]* D[phi] - V([phi]) - (1/4)FFuv
This new Lagrangian is now invariant under the U(1) gauge transformation.
[phi](x) -> [phi]'(x) = [phi](x)eiq[xi](x)Au(x) -> A'(x) = Au(x) + [partial derivative][mu][xi](x)
with [xi] any differentiable function. Continuing in exactly the same way as for the Goldstone model with a negative and expressing the Lagrangian in terms of the variables and as defined in the Lagrangian above, the result is
L = (1/2) ([partial derivative][mu]) [sigma] ([partial derivative][mu])[sigma] -[lambda](v2)([sigma]2) + (1/2)([partial derivative][mu])[eda]([partialderivative][mu])[eda] - (1/4)(Fuv)(Fuv) + (1/2)(q2)(v2)(A[mu])(A[mu])+qv(A[mu])([partial derivative][mu])[mu] + higher terms
The Lagrangian clearly has a massive vector boson field A and two scalar fields [sigma] , [eta] with [eta] massless, but unfortunately also a term A which does not fit in. It can not be understood as a perturbative interaction term since it is quadratic in the fields, as the terms for the free field are. However, a careful analysis shows that the Lagrangian has one degree of freedom too much. This extra degree of freedom can be absorbed by choosing a specific gauge, i.e., performing a gauge transformation, where (x) has the form
[phi](x) = ([squareroot of 2]/2)[v + [sigma](x)]
Such a gauge transformation is always possible and the chosen gauge is called the unitary gauge. In this gauge the field disappears and what is left is the Lagrangian
L = (1/2)([partial derivative][mu])[sigma]([partial derivative][mu])[sigma] -[lambda](v=2)([sigma]2) - (1/4)(Fuv)(Fuv) + (1/2)(q2)(v2)(A[mu])(A[mu]) + higher terms
Therefore, it is seen that a complex scalar field and a massless vector field, both with two degrees of freedom, as a result of the Higgs Mechanism were transformed into one real scalar field with one degree of freedom and a massive vector boson field with 3 degrees of freedom. A massless spin 1 particle has two transverse polarized states while a massive spin 1 particle has an additional longitudinal polarized state. It should be noted that the field only disappears if the bosons are massless. This requires the vacuum state to be degenerate, i.e., the Higgs Mechanism will only work with a degenerate vacuum.
The Higgs Mechanism was demonstrated here for a U(1) gauge invariant Lagrangian. To extend it to the SU(2) x U(1) gauge invariant Lagrangian of the electroweak theory is relatively simple. The starting point is a Lagrangian with a complex scalar doublet and four massless vector bosons. Counting degrees of freedom gives four from the scalars and eight from the vector bosons.
Through the Higgs Mechanism, the Lagrangian is transformed into one real scalar, three massive vector and one massless vector boson. The massless vector boson is, of course, to be identified with the photon and the single remaining scalar with the Higgs boson. Counting degrees of freedom again gives one from the Higgs, two from the photon and nine from the massive vector bosons, again adding up to twelve.
Introducing the masses of the vector bosons with one doublet of complex scalars is the simplest scenario. In principle, an infinite number of scalar fields can be introduced. The simplest supersymmetric models, instead, have five scalar fields left after the Higgs Mechanism, a doublet of charged scalars, two neutral scalars and one neutral pseudoscalar.
The masses of the particles in the standard model are given as
mH = (squareroot of 2[lambda])v, mW = vg, mZ = (mW)/(cos [theta]w)
where g is the weak coupling constant and the Weinberg angle. Using
v2 = (squareroot of 2)/(2Gf), [alpha] = ((g2)sin2([theta]w))
where Gf is the Fermi constant, the vector boson masses can be expressed through Gf, [alpha] and sin [theta]w. With the Fermi constant measured from the muon lifetime and the Weinberg angle from the relative cross sections of neutral current ( vu + p -> vu + X) and charge current (v[mu] + p -> [mu] + X ) processes, it was possible to predict the masses of the vector bosons. Their discovery at the UA1 and UA2 experiments at the CERN Sp S was a great victory for the electroweak theory.
Theoretical investigations that have sought to unify the fundamental forces of nature can now peer even farther back than the first millisecond into the history of the Universe. The theories are called Grand Unified Theories (GUTs) because they attempt to understand the electromagnetic force, the weak force, and the strong force as distinct low energy manifestations of a single underlying phenomenon. Attempts to include gravity as well, are called Theories of Everything (TOEs), and string theory is the leading candidate. There are precedents in physics for such a unification. In the 19th Century, James Clerk Maxwell unified the theories of electricity and magnetism. In the 1960's, a deep connection was found between the weak force and electromagnetism.
The simplest of the Grand Unified Theories was developed by Howard Georgi and Sheldon Glashow of Harvard University in 1973. It is called minimal SU(5). The designation SU(5) refers to the mathematical group of symmetries on which the theory is based. It is minimal in that it is the theory with the fewest adjustable perameters which must be assigned a value by experiment. According to minimal SU(5), the strong, weak, and electromagnetic forces, which seem very different under ordinary circumstances, become indistinguishable when particles interact with an energy of approximately 1015 billion electron volts (GeV). This energy exceeds the capability of even the largest planned particle accelerators by a factor of 10 trillion, and it is unlikely that such an energy will ever be achieved in the laboratory. It might seem that such a theory can't be tested but this is not the case. The theory has definite consequences at readily accessible energies.
The theory provides a rationale for several established features of the physical world that have long seemed mysteriously arbitrary. It accounts for the quantization of electric charge, which is the observation that charge always comes in discrete multiples of a fundamental smallest charge. It gives a value for the relative strengths of the three forces, measured at ordinary laboratory energy, that is in reasonably good agreement with experimental results. The theory predicts new phenomena that can't be deduced from earlier theories. The most noteworthy example is the decay of the proton.
In quantum electrodynamics, the interaction of two charged particles, such as two electrons, is related to the exchange of a third particle. The intermediate particle is the photon. It is different than a normal photon in that it does not transmit momentum from one particle to another, and is therefore called a virtual photon. It does this through the uncertainty principle introduced into quantum mechanics by Werner Heisenberg. The uncertainty principle does not invalidate the conservation laws of energy and of momentum but it does allow a violation of the laws to go unnoticed if it is rectified quickly enough.
In electromagnetism, the charged particles are either attracted or repelled by the exchange of a virtual photon but the particles are not otherwise altered. For instance, their charge is not changed. Therefore, the photon itself has no charge. Otherwise, it would carry charge from particle to another. The photon itself is massless. Therefore there is only one type of photon, and electromagnetism has the simplest form of symmetry, which is U(1) symmetry. The 1 refers to the fact that the photon interacts with only one particle at a time. The photon never transforms one kind of particle into another kind. The strong and the weak force are more complicated in this respect, and therefore have more complicated groups. The U stands for unity. You could graphically represent this by a square representing the photon, with an electron to the left, and another above it. You could think of the electron on the left as the particle that emitted the virtual photon, and the electron above it, as the particle that absorbed it. You could also think of the electron on the left as a particle before the exchange, and the electron above it, as one after the exchange, and is exactly the same.
The prevailing theory of the strong force is quantum chromodynamics (QCD). It was modeled directly on quantum electrodynamics. The "chromo-" signifies that the force acts not between electric charges but between color charges. As in QED, the magnitude of the force between two charges is proportional to the product of the charges. Particles that have no color charge are not subject to the force. A dimensionless coupling constant defines the intrinsic strength of the interaction. The coupling constant is much larger than the constant of electromagnetism, as might be expected for a force named strong.
Whereas electromagnetism is associated with just one kind of charge, the strong force acts on three colors: red, green, and blue. Each color represents a combination of underlying color charges. There are three kinds of color charge, red minus green (R-G), green minus blue (G-B), and blue minus red (B-R). Each charge can have a value of +1/2, -1/2, or 0, and each color of quark is distinguished by a particular combination of values. A quark is red if it has an R-B charge of +1/2, a G-B charge of 0, and a B-R charge of - 1/2. A green quark has the color charges R-G = -1/2, G-B = +1/2, and B-R = 0. In a blue quark, the three charges are R-G = 0, G-B = -1/2, and B-R = +1/2. The anticolors associated with the antiquarks are formed simply by reversing the signs of all charges.
The mechanism by which the strong force is transmitted is comparable to the corresponding mechanism in electromagnetism. The interaction between two charged particles is described by the exchange of a third particle. Whereas QED has a single massless photon, QCD has eight massless gluons. Furthermore, whereas the photon has no electric charge, some of the gluons do have color charge. The presence of a charged carrier fundamentally alters the character of the force. It means that the virtual particle can carry charge from the transmitting particle to absorbing particle, and so the charge of both particles is altered.