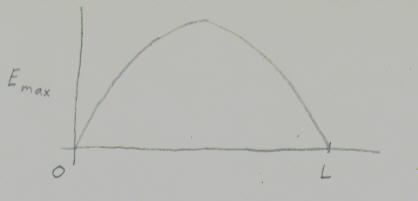
Newton believed that light was a particle. Fresnel showed that light was a wave. Einstein showed that the photoelectric effect and the compton shift could be best explained by saying light was a particle. Yet it was obviously a wave also so this created a dilemma. How could light be both a particle and a wave? Later it was shown that not just photons but all particles, such as electrons, are both particles and waves. Let me show how these two things come together. Let's say you had light bouncing back and forth between two parallel mirrors. Let's deal only with the mode of oscillation that has the longest wavelength. Half of it's wavelength fits between the two mirrors, so it's wavelength is 2L. You can see the wave if you graph the electric field for the length between the two mirrors.

[Just to get it out of the way here, epsilon looks like "E", psi looks like a trident, and nu looks like "v".]
Let's take the square of this and graph E^2 for this same oscillation.
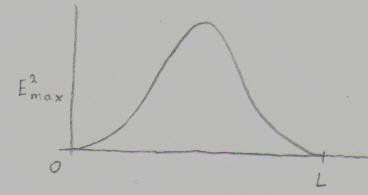
E^2 appears in a different context. The energy density U is the potential energy per unit volume. U=1/2[epsilon]E^2 where [epsilon]=8.85x10^-12 F/m. Therefore the above graph is a plot of the energy density in the standing electromagnetic wave.
If you think in terms of particles, each photon has the same energy E=[nu]h, where [nu] is the frequency, and h is Planck's constant, which is 6.63x10^-34 Js. If you have the energy density changing throughout the length but it's bound up in particles, each of the same energy, the density of particles will change throughout it's length. Thus the square of the wave amplitude at any point in a standing electromagnetic wave is proportional to the density of photons at that point. Photons are densest exactly between the two mirrors and fewest right next to the mirrors. Thus we've shown the connection between light as a wave and light as a particle. These graphs equally accurately describe an electron in an infinite potential well.
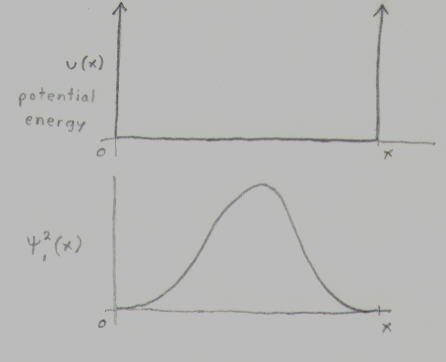

U(x)=0
E=(n^2)(h^2/8ml^2) where n=1,2,3... are the different nodes.
[psi]^2(x) is proportional to the probability of finding an electron in the interval between x and x+dx. [psi]^2(x) is the square of the wavefunction, or the probability density. Since the electron will be somewhere between 0 and x, the integral of [psi]^2(x)dx from 0 to L, will be 1.
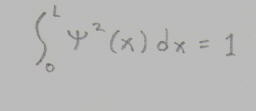
Here I plot the potential energy and the probability density for the more realistic case of a hydrogen atom.
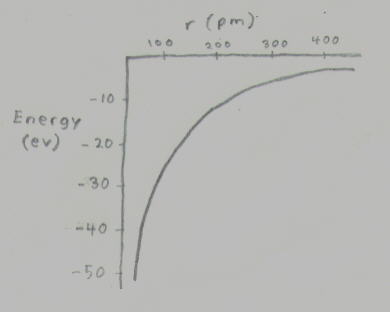
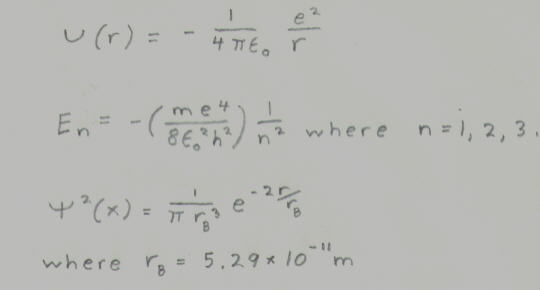
U(r)=(-1/4[pi])(e^2/r)
E=-(me^4/8[epislon]^2h^2)(1/n^2) where n=1,2,3...
[psi]^2(r)=(1/[pi](rB)^3)(e^(-2r/rB) where rB=Bohr radius=5.29x10^-11m
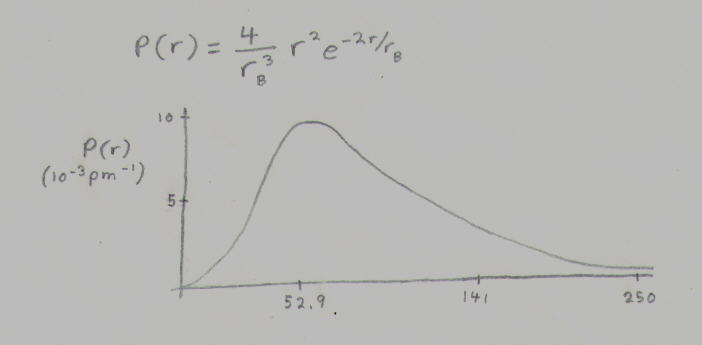
The radius of the highest probability density is the Bohr radius or r=52.9 pm. 68% of the time the electron will be closer than this and 32% of the time it'll be farther away. 90% of the time, it'll be within 141 pm of the proton. The Bohr radius, the distance of highest probability density, is the famous s orbital from chemistry. The atoms of other elements of course have far more complicated shells but they're all of a similar statistical nature. These characteristics of the subatomic or quantum world, probablity, uncertainty, as well as the fact that the act of measuring something alters what is being measured, is referred as the Copenhagen interpretation.
The Young double slit experiment established the wave nature of light. Let's imagine a Young double-slit expirement for electrons. A beam of electrons falls on a barrier with a double slit and sets up a pattern of interference fringes on a screen.
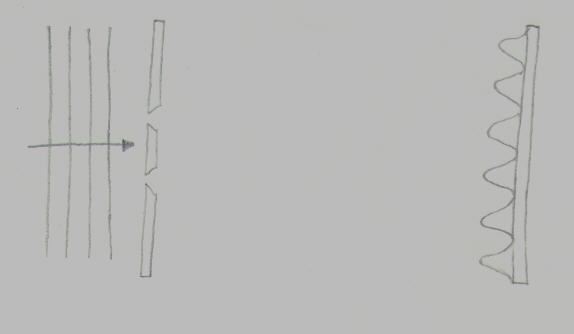
You could have a screen filled with electron detectors. It would seem that we are observing both the wave nature and the particle nature of the electrons. The interference pattern is a manifestation of the wave nature. The impacts registering on the particle detectors are a manifestation of the particle nature. However the particle nature includes not just the final destination of the electrons but their entire trajectory. Can we determine their entire trajectory, or at least which slit they pass through? We can place a transparent electron detector in front of each slit so we can detect whenever an electron passes through the slit. When we do that the interference pattern suddenly vanishes. When you detect the particle-like attributes of the electrons, you can no longer detect the wave-like attributes. When you detect the wave-like attributes, you can no longer detect the particle-like attributes. It's theorectically impossible to simultaneously observe the particle and wave-like forms of electrons, photons, or anything else.
The electrons, as matter waves, form, through constructive and destructive interference, the interference pattern on the screen. You can think of the matter waves as guiding the particle form of the electron, their connection with the particle being that the square of their associated wave function at any point measures the probability that the particle will be found at that point. Thus electrons pile up on the screen at those places where the probability is large, and are rare where the probability is small. The interference is caused by two matter waves passing out of the slits at once, or several electrons passing through the slits at once. What if you had only one electron passing through the slits at once? You might think that you don't get an interference pattern, but actually you get one anyway. The matter wave of the electron interferes with itself. In other words, a single electron passes through both slits simultaneously. Let's say you have a single electron passing through both slits. Then you look to see which slit it passes through. At that instant, it only passes through one slit, and the interference pattern disappears. This is called collapsing a wave function. One common interpretation is that before you look to see which slit it passed through, you had two realities superimposed on top of each other, one in which it went through one slit, and the other in which it went through the other slit. When you look to see which slit it passed through, and the wavefunction collapses, one of the two realities ceases to exist, leaving only the other one, where it went through the other slit.
This is the basis of the famous Schrodinger's Cat paradox. You could imagine if the electron went through one specific slit, a hammer broke a canister of cyanide in a box containing a cat, and if it went through the other one, nothing happened. The reality in which the cat is alive, and the reality in which the cat is dead, would be superimposed on top of each other until you check to see which slit the electron went through. When you check to see, one of the two realities will cease to exist leaving only the other one. A more important aspect of the double slit experiment is that which slit the electron goes through when you collapse the wavefunction is totally random. It has a 50% likelihood of going through one, and a 50% likelihood of going through the other. This randomness is derived from the statistical nature of particles. For instance, the Schrodinger's Cat paradox is usually described invoking radioactive decay. An alpha particle, which is a helium nucleus, has a given likelihood that it will barrier tunnel out of a 238U nuceus in a given interval of time, but whether it will or not is random. The likelihood of an electron being at a certain position in an infinite well or a hydrogen atom is what it is, but whether it will actually be there or not is random. Not only that, but you can't determine both its position and its momentum. The more accurately you know its position, the less accurately you know its momentum. The more accurately you know its momentum, the less accurately you know its position.
This is called the Heisenberg Uncertainty Principle. Let's say you have a particle and [delta]x is the uncertainty in your measurement of its position, and [delta]p is the uncertainty in your measurement of its momentum. ([delta]x)([delta]p)>h/2[pi] where h is Planck's Constant. h=6.63x10^-34 Js. If you pin down the position accurately, you won't be able to measure its momentum very well. If you improve the precision of the momentum measurement, the precision of the position measurement will deteriorate. Just as the Heisenberg Uncertainty Principle gives uncertainty for position times momentum, it gives uncertainty for energy times time. ([delta]E)([delta]t)>h/2[pi]. If you try to measure the energy of a particle within the interval of time [delta]t, your measurement will be uncertain by [delta]E=h/2[pi][delta]t. To make it more accurate, you have to measure it over a longer period of time. Over smaller intervals of time, the amount of energy of a partcle is less and less precise. Thus in smaller and smaller intervals of time, the energy available could be larger and larger. In very small intervals of time, the energy of a particle could be large enough to create another particle. Thus particles can emit other particles using the imprecision of their energy during short intervals. Of course the energy for the particle's creation must come from somewhere, and it's provided by the particle being reabsorbed by the original particle before the time interval expires. The fact that the energy for its creation is provided by its annihilation, after its creation, is allowed by the imprecision of the particle's energy during short time periods, meaning the Heisenberg Uncertainty Principle. Similarly particle-antiparticle pairs of all types are constantly emerging spontaneously from the vacuum, and promptly colliding and annihilating, the energy for their creation being provided by their annihilation.
The closer two particles are together, the less time it takes for a particle to be emitted by one, transverse the distance between them, and be absorbed by the other. Thus over shorter and shorter distances, you are dealing with shorter and shorter time periods, can borrow more and more energy, and can emit and absorb increasingly heavier particles. Over very short distances, two particles can exchange a virtual particle so heavy, the last time there was enough energy for it to be freely created was shortly after the Big Bang. For instance if two quarks happened to stray within 10^-29 centimeter of each other, an X particle could be exchanged between them. X-particles can convert quarks to leptons, and vice versa, and are so heavy, they only existed shortly after the Big Bang. Probing very short distances is like going back to the early Universe.
The Heisenberg Uncertainty Principle is based on imprecision and thus randomness. Whether a 238U nucleus will emit an alpha particle in a given interval of time is random. If you collapse a wavefunction, what it ends of being is random. With the double slit experiment, when you look to see which slit the electron went through, which slit that is, is random. There is a difference between random from our point of view and truly random. When you flip a coin, whether it's heads or tails is random from our point of view but it's not truly random. It's determined by the way you flip the coin, the force on the coin, how the force is applied, the weight of the coin, its trajectory through the air, air currents acting on it, how you catch it, and a large number of other factors. If you knew all these things and calculated it, you'd know if it was heads or tails without looking. Without knowing these things, it's as if it's random, but it's not truly random. It's determined by things. With collapsing the wave function of the double slit experiment, it is truly random.
There's an alternate explanation for collapsing wavefunctions, such as for the double slit experiment, called the Everett Many Worlds Principle. According to this, when you look to see which slit the electron went through, you see that it went through one and not the other. Unbeknownst to you, in another universe, you are witnessing the electron having gone through the other slit and not the first one. When you looked to see which slit it went through, the entire Universe divided into two universes, one in which it went through one slit, and one in which it went through the other slit. The two universes are forever independent and can never affect each other in any way. When you looked to see which slit it went through, not only did you become two people in different universes, but hundreds of distant galaxies were duplicated into presumably identical versions. Since wavefunctions are collapsing all the time all over the Universe, the Universes is continually dividing into an infinite number of universes. Laugh as you will, but this is entirely equivalent to the Heisenberg Uncertainty Principle, and the belief that the electrons selects one of the two slits at true random. The viability of a theory in physics is determined by the extent to which it could explain what you observe. These two theories explain what we observe equally well. Physicists would have no reason to favor one over the other.
Even though the true randomness theory and the many worlds theory don't contradict what we observe, we are uncomfortable with both of them for different reasons. True randomness seems to contradict the premise of physics itself. Physics is based on the premise that there's a reason for everything, even if we don't know what it is. For instance, when exotic hadrons were first discovered, we didn't know what they were, or what the patterns in the characteristics meant. Later we developed the theory of quarks, and learned the answers to those questions. Before we knew the answers, we knew there existed answers. Today we don't know why the speed of light has the value it does, 2.99x10^8 m/s, as opposed to some other value. It has to do with what happened before 10^-43 seconds after the Big Bang. We may never know the answer to that question. However there exists a reason even if we don't know what it is. Physics rests on the reassurance of that conviction. The alternative would be mythology, where things are the way they are just because that's the way they are. However, with true randomness, you have things where that's the way they are just because that's the way they are. If you ask, "Why did the electron go through this slit instead of the other one?", there does not exist an answer in the Universe. It's not that we don't know what the answer is. It's that there literally does not exist an answer. Once you accept that there are questions for which there are no answers, what prevents you from saying that all questions have no answers? It contradicts the reason we do physics at all. It contradicts what we're doing.
However, the absence of true randomness in the Universe would cause a different problem. When you do a classical experiment or look at any classical system, you assume that there is no randomness in the system. How do you change the final result? You can alter the initial conditions or the boundary conditions. The initial conditions are the way things are in the beginning, and the boundary conditions are the ways the system is affected by the outside. The way the components interact is governed by physics which you can not change. In a high school chemistry experiment, changing the initial conditions would be changing what you put in the flask before you begin the experiment. Changing the boundary conditions might be changing the length of time you hold the flask over the bunsen burner. These would cause the results to be different. The formation of the Solar System was very greatly affected by the initial conditions. It was the type of chaotic system that was very sensitive. Slight changes in the turbulence of the swirling matter would have caused the planets to end up being very different. The initial conditions were the amounts, densities, and distributions of the various elements in that part of the galaxy at that time. Our solar system has not been much affected by boundary conditions. External forces acting on the Solar System include the gravitiational attraction of nearby stars, the weak magnetic field of the galaxy, cosmic rays, and interstellar gas and dust that enters our solar system. If these had been different, the Solar System would be very slightly different today.
How might the Universe have ended up being different? Could the initial conditions have been different? At t=0, the Universe was a zero dimensional mathematical point. There is no information contained within a mathematical point. Therefore there really are no initial conditions. That couldn't have been different. Therefore you couldn't change the initial conditions. Could the boundary conditions have been different? As far as we know, our universe consitutes the entirety of reality. We observe nothing that implies otherwise. Therefore there is no outside to act on the Universe. The only boundary condition is nothing acting on the system. It can't be otherwise. Therefore there really are no boundary conditions. Thus you can't change the boundary conditions. If the initial conditions couldn't have been different, and the boundary conditions couldn't have been different, then the conclusion is the way the Universe turned out couldn't have been different. When you deal with a classical system, you neglect quantum effects. Of course in the real Universe there are quantum effects, and thus true randomness. The existence of true randomness creates a situation where the Universe could have turned out differently. Since the initial conditions and boundary conditions are fixed, we rely on true randomness to prevent the conclusion from being fixed.
I described how the existence of true randomness is uncomfortable. The nonexistence of true randomness would probably be more uncomfortable. What that would mean is that there would be no way the Universe could have turned out differently than it did. It had to end up with the four forces, the three generations of quarks and leptons, the large scale structure, etc. However, it's more than just that. It would also mean that George Bush had to be president. Every detail of the history of the Universe would be predetermined. According to this, every detail of your personal life was predestined even if nobody ahead of time knew what it would be. The fact that George Bush was elected, for instance, was incorporated into the Big Bang. This doesn't actually contradict anything we observe but it's highly disconcerting. People would very much rather this was not the case. People also have a distaste for the Everett Many Worlds principle. The many worlds view forces you to accept the reality of an infinite number of parallel universes each of which are continually dividing into an infinite number of universes. You have to accept the reality of an infinite number of versions of yourself. People have a difficult time accepting that. Keep in mind that the Heisenberg Uncertainty Principle and the Everett Many Worlds principle don't actually contradict what we observe. This is one of the few times that theories in physics don't contradict what you observe. Usually we do everything we can to decrease the extent of contradiction between what your explanations state you should observe and what you actually observe. Here the theories don't contradict what we observe but we still don't like them. They don't cause problems for physics but for psychology. People just don't like them.
What I've discussed so far was developed in the 1920's. However in the 1950's, D.Bohm and others developed an alternative to the Copenhagen line of thought which involves true randomness and the many worlds picture, called the pilot wave interpretation. In this model, quantum dynamics is made much more similar to classical dynamics. In physics, the Lagrangian defines the theory. The Lagrangian is a single function that determines the dynamics, must be a scalar in relevant space, and must be invariant under transformations since the action is invariant. The Hamiltonian associated with a Langrangian L is H=(q overdot)(partial deivative of L with respect to q overdot)-L where q overdot is the derivative of q with respect to time. The Hamilonian-Jacobi equation is
[I'll type the partial derivatives as if they were full derivatives, but just keep in mind that they're really partial derivatives. Nabla's are triangles pointed down. All m's and nabla's of "of n" All summations are over n.]

dS/dt=-H(q,dS/dt,t)
A set of N nonrelavistic spinless particles are described by their spatial coordinates x={x,...xN}. The wave function [psi] of this system obeys the Scrodinger equation.
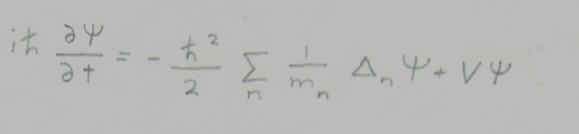
ih(d[psi]/dt)=-h^2/2(summation of (1/(m of n))([delta][psi]+V[psi]
where V=V(x) is the particle interaction potential. If you reprsent the wavefunction in polar form, the phase S(x,t) and the amplitude R(x,t) satisfy the system
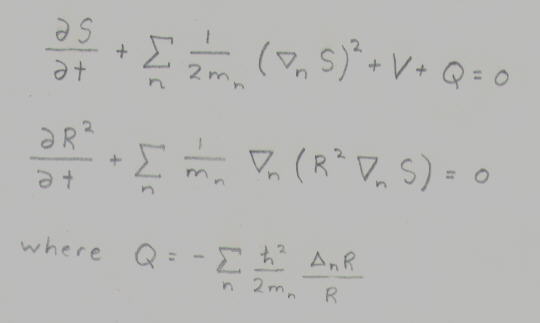
dS/dt+summation of (1/2m)([nabla]S)^2 + V+Q=0
d(R^2)/dt+summation of (1/m)[nabla](R^2[nabla]S)=0
where Q=-summation(h/^2/2m)([nabla]R/R)
Look at the first of the last two equations.
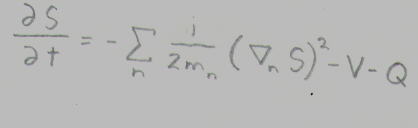
dS/dt=-summation (1/2m)([nabla]S)^2-V-Q
This is the same as the classical Hamilton-Jacobi equation except that it contains the term Q. Thus you've made quantum mechanics the same as classical mechanics except that it contains an extra term. Q(x,t) is the quantum potential. In the limit in which the quantum potential can be neglected, we recover classical evolution. Thus the new formation of quantum theory can be regarded as just a deformation of the classical dynamics. The classical limit in the dynamics of a phtsical system is achieved for those configuration variables for which the quantum potential becomes neglible. In this interpretation, the temporal dynamics of the particle coordinates and bosonic field configurations completely determine the state of the physical system whether it's microscopic or macroscopic. Therefore the description of all the physical systems has become unified. In the pilot wave formulation of quantum mechanics, the measurement process is regarded as just a partial case of the generic evolution guided by a wave function that obeys the Schrodinger equation. The probabilistic character of the measurement arises from our ignorance of and inability to control the actual initial values of the particle and field configuration variables in each system of an ensemble as well as the measurement apparatus.
You use the same equations to describe quantum and classical dynamics. The quantum dynamics are not fundamentally different from the classical dynamics. When you flip a coin, whether it's heads or tails is determined by a very large number of small factors, such as the force with which it's flipped, the way it's flipped, etc. From our point of view of not knowing these factors, it appears random and we can only use statistics. When you put an electron through a double slit experiment and check to see which slit it went through, which slit it is, is determined by a very large number of infintesimal factors, where we don't even have any idea what they might be. From our point of view of not knowing these factors, it appears random and we can only use statistics. Thus seeing which slit it went through is not fundamentally diffferent then flipping a coin. Thus you've solved the fundamental problems of quantum mechanics. You've gotton rid of true randomness, in other words, the idea that there exists questions for which there do not exist answers. We were able to preserve the basic tenet of physics which is that there exists a "why" or reason for everything even if we don't know what it is. Futhermore we achieved this without invoking an infinite number of parallel universes, or believing that there exists an infinite number of versions of yourself. Unfortunately this victory is tempored by the fact that removing true randomness is a double edged sword. You have all of the negative aspects of the lack of randomness that I described earlier. Without it, you're forced to contend that every single event in the Universe was predestined.
Thus we're left to choose from three undesirable choices. First you could choose to believe in the traditional Heisenberg Uncertainty Principle and Copenhagen interpretation that involves true randomness. You don't have to believe that there exists an infinite number of you or that every event in your life was predetermined. It doesn't actually contradict what you observe. However it eats away at the foundation of physics itself. Physics is based on the premise that there exists answers to our questions. That's why we seek these answers. There's a reason for everything even if we don't know what it is. To say that there is no reason why an electron went through one slit instead of the other is to say that there are things for which there is no reason. That sounds like something from mythology or religion, but that's what you have if you say there's true randomness.
Second, you could choose to believe in the Everett Many Worlds principle. From your point of view of inhabiting one of the universes, you feel like there's randomness, but from the point of view of all of the universes, there isn't true randomness. Since all possible versions of your life are equally possible (and indeed do exist) not every detail of your life was predetermined. The life that you expirence was not preselected. Simultaneously, from your point of view, there's randomness. However, you have to accept the reality of an infinite number of parallel universes, each of which is constantly dividing into an infinite number of other parallel universes, and an infinite number of versions of yourself. This doesn't actually contradict what we observe but people don't like the idea.
Third, you could choose to believe in the pilot wave interpretation. Everything is caused by something even if we have no idea what it is, so there isn't true randomness. You don't have to believe in an infinite number of versions of yourself. However, if there isn't true randomness, that means that every event in the Universe, every detail of human history and your daily life, had to happen, and was predestined. Free will is an illusion. If you go and get a drink of water, it's not just because you wanted to, but because it was incorporated into the Big Bang. Everything is predetermined even if nobody knows what it is. This doesn't actually contradict what we observe but people don't like the idea.
So there are the three choices. It's interesting that in physics, the problem is usually getting rid of contradictions between what our theories state that we should observe and what we actually observe. Our most advanced theories, supersymmetry, superstrings, D-branes, etc., although great achievements, are wracked with problems. They contradict themselves, each other, and what we observe in myriad of ways. This is to be expected when you're dealing with modern physics. We try to decrease the extent of contradiction between what our explanations state we should observe and what we actually observe. We try to compactify extra dimensions, etc. However, the three theories I described don't contradict what we observe at all. The problem is not one of physics but of human psychology. We feel uncomfortable with these theories. We don't want to think that any of them are true. If it's any consolation, none of them are.
Most of what I've said so far is based on the concept of particle-wave duality, that photons and electrons are both waves and particles, which is false. It is often said that light is both and particle and a wave. In reality, it's neither a particle nor a wave. It's a subatomic entity that is in no way similar to anything in the macroscopic environment. For centuries there was a debate as to whether light was a particle or a wave. People would imagine it as either like tiny marbles or like waves on the ocean. Then it was decided that light was both a particle and a wave. At first it was believed that it went back and forth.