The Standard Model

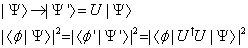
Particle physics is described using the mathematics of group theory so I'm going to first explain what that is. In pure mathematics, they try to go from the specific to the general, encapsulated by the joke "Let 2 = x". In that vein, they try to generalize from specific operations on specific quantities to general operations on general quantities. Group theory is the study of generic operations on generic quantities. The quantities could be numbers, vectors, tensors, spinors, matrices, etc. In order to be a group under group theory, it must meet four criteria.

1. There must be some operation that you can perform on two members of the group to yield a third member of the group. AB = C where A, B, and C are members of the group. We are not assuming that the operation is commutative, namely we do not assume AB = BA

2. The operation must be associative, meaning the order does not matter. A(BC) = (AB)C

3. There must be an identity element where if you do the operation on a member of the group and the identity element, you get the same member of the group. AI = A In the addition of numbers, the identity element is 0. In multiplication, it is 1.

4. There exists an inverse of each element where if you do the operation on an element and its inverse, you get the identity element. AA^-1 = I For instance, in addition, a + (-a) = 0, and in multiplication, a x (1/a) = 1.

If a group also meets the commutivity relation AB = BA, it's called an Abelian group. Here are the definitions of group-like objects. A famous type of group is a lie group. It was named after Norwegian mathematician Marius Sophus Lie (1842 - 1899), and is pronounced "Lee". The easiest way to explain it is through the concept of rotations. Let's say you have a 3-D graph. You could rotate whatever is there about any axis, such as the x-axis, y-axis, or z-axis. You draw any line in 3-D space, and then rotate around that line. Now let's say you rotate about any line by a given angle, and then rotate again by another angle. If you add the angles together, you get a third angle, and the result is the same as if you had initially rotated by that angle. Therefore, all angles could be considered members of the group, and the adding of angles is an operation that can be performed on those angles. The order in which the rotations are performed doesn't matter so it obeys the associative rule. The identity element is simply no rotation at all. The inverse of a rotation is rotating by the same amount in the opposite direction. Therefore, if you rotate by a given angle, and then rotate back by the same angle, it's the same as if you hadn't rotated at all. Therefore, these rotations form a group called a Lie group. In this system, any rotation can be thought of as made of an infinite number of infinitesimal rotations.

In physics, you assume the results of a system are independent of the coordinate system used. If you rotate a laboratory apparatus, it should have no effect on the result of the experiment. Therefore, the rotation could be called a symmetry, and the physics is invariant under that symmetry. Rotation is a subset of the Lorentz transformations.

This is how you would write that down. The probability that a system described by | Ψ > will be found in a state | φ > must be unchanged by rotation R.

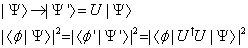
| [phi] > -> | [phi]' > = U | [phi] >

| < [phi] | [psi] > |² = | < [phi]' | [psi]' > |² = | < [phi] | U^†U | [psi] > |²

where U is any unitary operator. It simply states the fact that the system is unchanged by the rotation. U^†U means it's unchanged by a rotation in either direction. You can define an operator for each possible rotation U(R₁), U(R₂), etc. and these form a group analogous to the group of rotations R₁, R₂, etc. This group is called the unitary representation of the rotation group.

The Hamiltonian of a system is also unaffected by rotation and that is written as

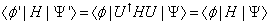
< [phi]' | H | [psi]'> = <[phi] | U^† H U | [psi]> = < [phi] | H | [psi] >

If you rotate in one direction and rotate back the other way, it cancels out, and is exactly the same.

H = U^† H U

In other words [ U, H ] = UH - HU = 0

All properties of the group follow from considering infinitesimal rotations around the identity. If no rotation is U = 1, then an infinitesimal rotation is

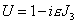
U = 1 - i[epsilon]J₃

where ε is the infinitesimal rotation and J₃ is the generator of rotations. Let's say we're rotating about the z-axis. Let's say you make infinitesimal rotations in either direction.

1 = [U dagger]U = ( 1 + i[epsilon][J₃ dagger]) ( 1 - i[epsilon]J₃)

= 1 + i[epsilon]([J₃ dagger] - J₃) + 0[epsilon]²

Now, you could either imagine this as keeping the axes fixed and rotating the physical system, or as keeping the physical system fixed and rotating the axes. A rotation of the physical system by θ is identical to a rotation of the axes by -θ. Therefore, the rotated wavefunction Ψ' at the unrotated coordinate r is the same as the unrotated wavefunction Ψ at the rotated coordinate R^-1r.

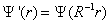
[psi]' (r) = [psi] (R^-1 r)

Therefore, you have a one-to-one correspondence between Ψ' and Ψ which we describe with the unitary representation.

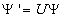
[psi]' = U[psi]

So now let's look at an infinitesimal rotation about the z-axis. The z-coordinate is kept the same, while x and y are rotated by an infinitesimal rotation ε.

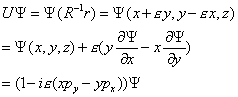
U [psi] (x, y, z) = [psi] (R^-1 r) = [psi](x + [epsilon]y, y + [epsilon]x, z)

= [psi](x, y, z) + [epsilon]( y[partial derivative of psi with respect to x] - x[partial derivative of psi with respect to y])

= (1 - i[epsilon](xp_y - yp_x))[psi]

Comparing with U = 1 - iεJ₃ you have

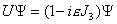
U[psi] = (1 - i[epsilon]J₃)[psi]

Therefore, we can identify the generator J₃ of rotations about the z-axis with the third component of the angular momentum operator.

The eigenvalues of the observable J₃ are constants of the motion. They are conserved quantum numbers. A symmetry of the system has led to a conservation law. The fact that experiments performed with different orientations of the apparatus give the same physics results has led to the conservation of angular momentum. This, of course, is the result of Noether's Theorem, invented by Emmy Noether in 1915, which says that for every continuous symmetry of the laws of physics, there must exist a conservation law, and for every conservation law, there must exist a continuous symmetry.

A rotation through a finite angle θ may be built up from a succession of n infinitesimal rotations.

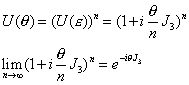
U([theta]) = U([epsilon])ⁿ = (1 + i([theta]/n) J₃)ⁿ

lim n -> infinity (1 + i([theta]/n) J₃)ⁿ = e^{-i[theta]J₃}

Now here we have done this whole thing for rotations around the z-axis, also called the 3-axis. You can do the same thing for the x-axis or 1-axis, to define J₁, as well as the y-axis or 2-axis, to define J₂.

You get the following results.

[ J₁, J₂ ] = iJ₃

[ J₂, J₃ ] = iJ₁

[ J₃, J₁ ] = iJ₂

You can write this compactly as

[ J_j, J_k ] = iJ_l

where jkl are cyclic permutations of 123. In fact, more generally you have

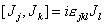
[ J_j, J_k ] = i[epsilon]_jklJ_l

where ε_jkl = +1 for a cyclic permutation of 123, -1 for an anticyclic permutation (321), and 0 otherwise. ε_jkl is called the structure constants of the group. The J's form a lie algebra.

Non-linear functions of the generators which commute with all generators are called Casimir operators. For the rotation group, the only Casimir operator is J² = J₁² + J₂² + J₃²

This is in fact, the definition of a Lie group. The elements of a Lie group are

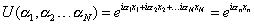
U([alpha]₁, [alpha]₂,…[alpha]_N) = e^{i[alpha]₁X₁ + i[alpha]₂X₂ +…i[alpha]_NX_N} = e^{i[alpha]_nX_n}

The N generators are Hermitian operators obeying a Lie algebra.

[X_a, X_b] = if_abcX_c

The generators form an N-dimensional vector space. Each generator is an operator in a Hilbert space parametrized by the angles α_a. The coefficients f_abc are the structure constants of the group.

There are many types of Lie groups. The following are the main ones.

Name	Algebra	Cartan Label	Number of Generators
Special Unitary	SU(n)	An-1	n2-1
Special Orthogonal	SO(n)	B(n-1)/2 if n odd Dn/2 if n even	(1/2)n (n-1)
Unitary Symplectic	Sp(n)	Cn/2	(1/2)n (n+1)

Then you have the exceptional groups, G₂, F₄, E₆, E₇, and E₈. There is an infinite series of simple Lie groups associated to rotations in real vector spaces which are the SO(n) groups, also called the B and D series. There is an infinite series of them associated to rotations in complex vector spaces which are the SU(n) groups, also called the A series. There is infinite series of them associated to rotations in quaternionic vector spaces which are the Sp(n) groups, also called the C series. The five exceptional groups are related to the octonions. The pure mathematics of Lie groups is excruciatingly complicated, and talks about things like nilpotent groups, etc. Here we'll only discuss what's used in particle physics. Most groups in particle physics are of the SU(n) type.

Elements of the SU(n) groups are represented by n x n unitary matrices. U^†U = 1 with det U = 1. Let's determine the number of independent parameters. There are n x n = n² elements. Each is complex. Complex numbers, a + bi, each have two parameters so that's 2n². U^†U = 1 imposes n conditions on the diagonal elements so that's 2n² - n. From that you subtract the number of independent elements which is half those not including the diagonal. n x n = n² elements minus n diagonal elements is n² - n. You take half of those so that's (n² - n)/2. You take twice that since they are complex 2[(n² - n)/2] = n² - n. Then subtract half those off the diagonal, n² - n, from the total minus the diagonal restrictions, 2n² - n.

(2n² - n) - (n² - n)

2n² - n - n² + n

2n² - n² = n²

Since det U = 1 is fixed, you end up with n² - 1 free parameters.

In particle physics, that is the number of bosons that mediate the force. The weak force is described by SU(2). 2² -1= 4 -1 = 3 bosons, which are the W⁺, W^-, and Z⁰. The strong force is described by SU(3), 3² - 1 = 9 - 1 = 8 bosons which are the 8 gluons. The minimal grand unified theory is SU(5). 5² - 1 = 25 - 1 = 24 bosons, which are the 12 bosons from the Standard Model, plus 12 new bosons which convert quarks to leptons and vice versa.

In the 2 x 2 case, the possible ways to parametrize U are

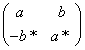
where a and b, which are called Cayley-Klein parameters, are complex numbers, and |a|² + |b|² = 1, or

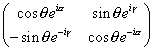
If H is Hermitian, meaning H commutes with H^†, then e^iH is unitary.

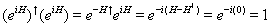
(e^iH)^†(e^iH) = e^-iH† e^iH = e^-i(H-H†) = e^-i(0) = 1

In a U(n) group, you have

U = e^iH

A subgroup of U(n) is the special unitary group SU(n). SU(n) has the further restriction that det U = 1

det U = det e^iH = e^{Tr H}

Tr H is the trace of the matrix H, which is the sum of the diagonal components. If the sum of the diagonal of H is 0, then H is called "traceless" and

det U = e^{Tr H} = e⁰ = 1

Here I show explicitly that det e^A = e^{Tr A}

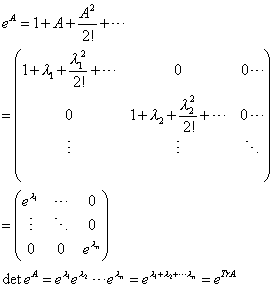
In the lowest dimension non-trivial representation of the rotation group, j = ½, the generators can be written

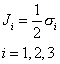
J_i = (1/2) [sigma]_i where i = 1, 2, 3

where σ_i are the Pauli matrices

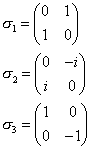
The basis for this representation is usually chosen to be the eigenvectors of σ₃ which are

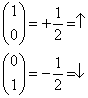
The first describes a spin ½ particle of spin projection up along the z-axis.

m = + ½ or up

The second describes a spin ½ particle of spin projection down along the z-axis.

m = - ½ or down

The Pauli matrices σ_i are Hermitian, and the transformation matrices are unitary.

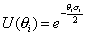
U([theta]_i) = e^{-[theta]_i[sigma]_i/2}

The set of all unitary 2 x 2 matrices is group U(2). The group of matrices U(θ_i) is smaller than this, and is represented by SU(2) which is a subset of U(2).

There are 1, 2, 3, 4, . dimensional representations of SU(2) corresponding to j = 0, ½, 1, 3/2, ... respectively. The two-dimensional representation is the Pauli matrices themselves. They are called the fundamental representation of SU(2), the representation from which all other representations can be built.

The Pauli matrices have a simple generalization to SU(3). For SU(3), there are 3² - 1 = 8 generators. They are called λ_a where a = 1, 2, ...8. The commutation relations are

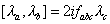
[ [lambda]_a [lambda]_b ] = 2if_abc[lambda]_c

where

f₁₂₃ = 1

f₄₅₈ = f₆₇₈ =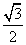

f₁₄₇ = f₅₁₆ = f₂₄₆ = f₂₅₇ = f₃₄₅ = f₆₃₇ = ½

All other f's are 0. f_abc is antisymmetric.

Here are the λ's. They are also called the Gell-mann matrices. Compare to the Pauli matrices.

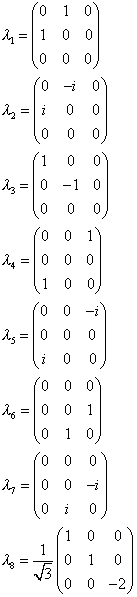
λ₃ and λ₈ are the only ones that are diagonal. σ₃ is the only one of the Pauli matrices that is diagonal. The number of Casimir operators is equal to the number of diagonal matrices.

A famous early experiment demonstrating the effects of quantum mechanics was the Stern-Gerlach experiment, performed by Otto Stern and Walther Gerlach in 1922. Let’s say you have a bunch of silver atoms in an oven, some of which escape through a small hole. The beam of silver atoms goes through a collimator, and then passes between two magnets, one of which has a sharp edge, so the beam is subjected to an inhomogeneous magnetic field. A silver atom has 47 electrons, 46 of which can be imagined to form a symmetrical cloud with no net angular momentum. Ignoring nuclear spin, the atom then has an angular momentum which is due solely to the intrinsic spin of the 47th electron, which is in the 5s orbital. The magnetic moment μ of the atom is proportional to the electron spin S. An atom with μ_z < 0, or S > 0, experiences a downward force. An atom with μ_z > 0, or S < 0, experiences an upward force. Therefore, the Stern-Gerlach experiment measures the z-component of μ, and thus the z-component of S. The atoms in the oven are randomly oriented. There is no preferred orientation of μ. If an electron were like a classically spinning ball, you would expect all values of μ_z to be realized between | μ | and -| μ |. You would then get one bundle of beams on the screen. Instead, however, the Stern-Gerlach experiment splits the original silver beam into two distinct components. This means that the electron spin S can only have two possible values of the z-component of S, which are spin up, S_z+, and spin down, S_z-. This shows that spin is quantized. In the same way, you could have split the beam into an S_x+ component and a S_x- component.

Now imagine that you do the Stern-Gerlach experiment, and divide the beam into S_z+ and S_z-. Now you let's say you stop the S_z- beam, and using only the S_z+ beam, you do another Stern-Gerlach experiment, this time with the inhomogeneous magnetic field in the x-direction, and you divide the S_z+ beam into its S_x+ and S_x- components. According to classical physics, you would expect each of these beams not to contain any S_z- component since you already removed it. Now let's say you stop the S_x- beam, and using only the S_x+ beam, do another Stern-Gerlach experiment, with the inhomogeneous magnetic field in the vertical direction. You might expect to only produce an S_z+ beam, but instead you produce both an S_z+ and S_z- beam. This shows that in quantum mechanics, you can't measure both S_z and S_x simultaneously. The selection of the S_x+ beam erases any previous information about S_z.

You can represent the spin state of the silver atom, or actually the electron, in a two-dimensional abstract vector space. You can represent the S_x+ state by a vector called the ket, written as | S_x; + >, which is a linear combination of two base vectors, | S_z; + >, and | S_z; - >, which correspond to the S_z+ and S_z- states. Then you have

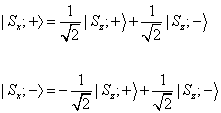
The 1/[squareroot of 2] factors are called Clebsch-Gordan coefficients.

If you have a function of a vector equal to a scalar times the vector, it takes the following form.

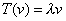
T(v) = [lambda]v

where T(ν) is the eigenfunction and is a linear operator, ν is the eigenvector, λ is the eigenscalar or eigenvalue, and λν is the eigenstate. "Eigen" is German for "his own" or "belonging to". The terms eigenvalue and eigenvector probably originate from the idea that they are special values or vectors belonging to a matrix.

This is the notation that is used in quantum mechanics.

A | i> = a_i | i >

where A is the eigenfunction, and is an operator, | i > is the eigenvector, and a_i is the eigenscalar. ψ is the wavefunction and is a function of position. | ψ > is an operator.

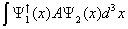
[integral] [psi]₁* (x) A [psi]₂ (x) d³x

can be written as

< 1 | A | 2>

A is an operator and can operate on 2, or its conjugate A^† can operate on 1. < 1 | is called the bra, and | 2 > is called the ket. Together, they form a bracket. Here you can read about bra-ket notation.

Kets are vectors in a complex vector space. Observables correspond to linear operators on that vector space. Physical states correspond to rays in this vector space, meaning that two kets represent the same physical state if and only if one ket is a complex number times the other ket. The 0 vector doesn't correspond to a physical state. The counterpart of the ket space is called the bra space. It is a complex linear space, and there is a 1-1 mapping between a ket and a bra which is called the dual correspondence, represented by flipping the Dirac notation.

The Hermitian conjugate of an operator is

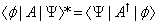
< [phi] | A | [psi] >* = < [psi] | A^† | [phi] >

If A = A^†, then A is a Hermitian operator.

If the eigenvalues are non-degenerate, the eigenfunctions are orthogonal, and can be defined to be orthonormal.

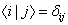
< i | j > = [delta]_ij

Such a set of eigenfunctions is called a complete set since any other state function can be expanded in terms of them.

Matrices have the same non-commutivity as operators and so can be used for the mathematical formalism of quantum mechanics. From matrix multiplication, where r is row, and c is column, you have

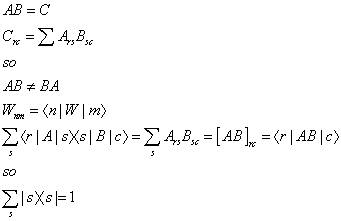
which is called the completeness relation.

In the Schrodinger wave formalism, the time dependence is on the waves or states, and the operators are constant. In the Heisenberg matrix formalism, the time dependence is on the operators, and the waves or states are constant. In both cases, the time dependent part depends on the Hamiltonian. In the Dirac formalism, which is sort of a hybrid, both the waves or states, and the operators, are time dependent and depend on the Hamiltonian. The waves depend on the interaction Hamiltonian, and the operators depend on the free Hamiltonian.

Paul A. M. Dirac (1902 - 1984) attempted to combine special relativity with Schrodinger's theory of wave mechanics. He took the following relation between kinetic energy and momentum.

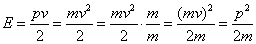
E = (pv)/2 = (mv²)/2 = ((mv²)/2) (m/m) = (mv)²/2m = p²/2m

Einstein's equation E = mc², and the mass of a particle as a function of rest mass

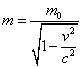
m = m₀/[squareroot of (1 - v²/c²)]

and used these to obtain the Klein-Gordon equation.

E² + p²c² = m₀²c⁴

Here the relationship between energy and momentum is symmetric because both are squared.

Erwin Schrodinger (1887 - 1961) derived the Klein-Gordon equation before inventing non-relativistic quantum mechanics. He actually used it to derive the fine structure constant of the hydrogen atom. However, he couldn't get it to work because the Klein-Gordon equation does not fully describe fermions. Only after that did he turn to non-relativistic quantum mechanics, and wrote the Schrodinger equation. You take the de Broglie hypothesis.

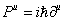
P^u = i[h bar][partial derivative]^u

where

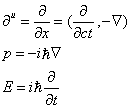
[partial derivative]^u = [partial derivative with respect to x_u] = ([partial derivative with respect to ct], -[nabla]) so p = -i[h bar] and E = i[h bar][partial derivative with respect to t]

and insert the substitutions into the energy-momentum relation E = p²/2m + V and you get

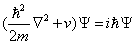
(([h bar]²/2m/)([nabla]^2/) + V)[psi] = i[h bar][psi]

Anyway, let's go back to the Klein-Gordon equation derived by Dirac.

E² + p²c² = m₀²c⁴

If you solve for E, you get

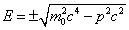
E = ± [squareroot of m₀²c⁴ - p²c²]

Now, the plus possibility means positive energy. The minus possibility means negative energy. Most people assumed that this negative solution was just a spurious result with no physical meaning. Dirac made the outlandish prediction that it refers to an actual particle that was an electron with negative energy. This particle was subsequently discovered by Carl Anderson in 1932 in a cloud chamber, and is called a positron.

In an atom, a photon can kick an electron from a lower to a higher level. Dirac imagined that there existed an infinite number of states below the lowest energy level in an atom, and they were all filled. A photon can kick an electron out of one of these states, and the positron is the hole left behind. When an electron falls into such a hole, a photon is released like an electron falling to a lower energy level in an atom. This was called the Dirac sea. We no longer imagine it like that, but we do imagine the vacuum as containing vacuum energy, and filled with particles continually coming in and out of existence. Dirac was the first to suggest a value for the vacuum energy, although his suggestion of negative infinity is obviously not accurate.

If you take Dirac's version of the Klein-Gordon equation.

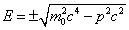
E = ± [squareroot of m₀²c⁴ - p²c²]

and make the normal operator substitutions we did earlier, you get

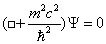
( [D'Alambert] + (mn²c²/[h bar]²))[psi] = 0

which is the normal way of writing the Klein-Gordon equation.

Dirac looked at his equation and thought that it must be possible to write it as a linear expression where the momentum p is a vector. He came up with

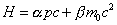
H = [alpha]pc + [beta]m₀c²

We saw before, the following notation.

[a, b] = ab - ba

This is called a commutator. The following defines an anticommutator.

{a, b} = ab + ba

If you insert the above Hamiltonian into the energy-momentum relation, then for self-consistency, α and β must obey the following relations.

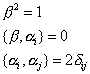
[beta]² = 1

{[beta], [alpha]_i} = 0

{[alpha]_i, [alpha]_j = 2[delta]_ij

There are no numbers that obey these relations. Most people would say there was no solution, but Dirac thought there must exist some entities that would meet these criteria. He suggested that α and β were operators whose existence suggested a new degree of freedom.

Dirac found that such entities did exist, and they were a set of matrices that had been developed earlier by Wolfgang Pauli who used them to describe electrons as spin ½ particles, where one complete rotation is 720°.

α and β are 4 x 4 matrices.

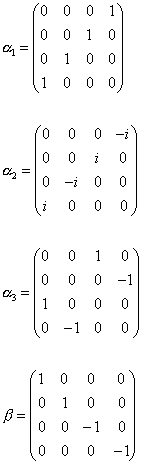
They are normally written down in Dirac representation.

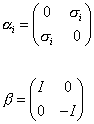
where σ_i are the three Pauli matrices.

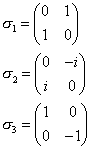
and I is the 2 x 2 identity matrix.

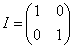
A less common representation created by Hermann Weyl is the Weyl representation.

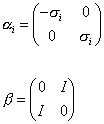
In these representations, the wavefunction is represented by a column vector called a spinor. It would be a digression to explain what exactly a spinor is but basically, it's a thing that has to go through a rotation of 720° to return to its original state. This can be demonstrated by several parlor tricks.

Using α and β, you can define the gamma matrices as follows.

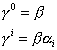
[gamma]⁰ = [beta]

[gamma]ⁱ = [beta][alpha]_i

They obey the following anticommutation relation.

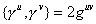
{ [gamma]^u, [gamma]^v } = 2g^uv

Using the de Broglie operator

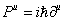
P_u = i[h bar][partial derivative]_u

The Dirac equation becomes

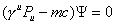
([gamma]^uP_u - mc)[psi] = 0

Sometimes you see the scalar product of a 4-vector with γ^u represented by a slash through the 4-vector.

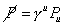
[P slash] = [gamma]^uP_u

The gamma matrices can be written to form a 4-vector.

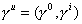
[gamma]^u = ([gamma]⁰, [gamma]^I

They obey the following relation.

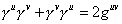
[gamma]^u [gamma]^v + [gamma]^v [gamma]^u = 2g^uv

Another quantity you can define is γ⁵

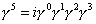
[gamma]⁵ = i[gamma]⁰[gamma]¹[gamma]²[gamma]³

At one time, some people had the gamma indices run from 1 - 4, so the next one would be 5. However, most people run them from 0 - 3, so now there is no γ⁴.

We can define the chirality operator.

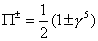
[pi]± = ½ (1 ±[gamma]⁵)

A state of definite chirality produces particles of one helicity in the massless limit. The weak interaction involves 1 - γ⁵ and thus produces only left-handed neutrinos.

In Dirac representation.

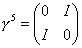
Another quantity you can define is the adjoint spinor [psi bar].

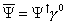
[psi bar] = [psi dagger] [gamma]⁰

The Hermitian conjugate denotes the complex conjugate of the transposed wavefunction. You take the vector transpose of the column vector ψ.

Using the following relations.

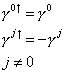
[gamma]^{0 dagger} = [gamma]⁰

[gamma]^{j dagger} = -[gamma]^j

j not equal to 0

you can write the Dirac equation in adjoint form.

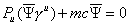
P_u ([psi bar] [gamma]^u) + mc[psi bar] = 0

Take the combination

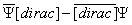
[psi bar] [dirac] - [dirac bar][psi]

This gives

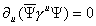
[partial derivative]_u ([psi bar] [gamma]^u [psi]) = 0

This suggests that

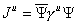
J^u = [psi bar] [gamma]^u [psi]

is to be interpreted as a probability 4-current.

You can call γ^u a 4-vector in the sense that [Ψ bar] γ^u Ψ, which is a scalar in spin space, transforms as a normal 4-vector, like p^u or x^u.

It's sometimes useful to define the following operators which can isolate left-handed or right-handed particles of a given type.

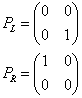
The following interesting chronology describes how these developments came about.

1. Erwin Schrodinger takes the formula E² = p² + m² for kinetic energy in special relativity, replaces energy and momentum by operators, and gets a wave equation, which we now call the Klein-Gordon equation.

2. Schrodinger uses the Klein-Gordon equation to solve for the energy levels of the hydrogen atom. He gets answers he dislikes, so he never publishes this, and he discards the Klein-Gordon equation.

3. In 1926, Schrodinger tries again, starting from the formula E = p²/2m for kinetic energy in Newtonian mechanics. He gets answers he likes, publishes this work, and becomes famous. This equation becomes known as the Schrodinger equation.

4. In 1926, Oskar Klein and Walter Gordon, seeking to extend Schrodinger's work to the relativistic case, reinvent the Klein-Gordon equation. It’s named after them since they published it first, even though Schrodinger derived it earlier.

5. People notice that the Klein-Gordon equation has negative-frequency solutions corresponding to the solutions of E² = p² + m² with E negative, and conclude something is wrong with the Klein-Gordon equation.

6. In 1928, Paul A. M. Dirac decides the Klein-Gordon equation has negative-frequency solutions because it's a 2nd-order equation, and invents a first-order equation to replace it, called the Dirac equation.

7. Dirac discovers that the Dirac equation also has negative-frequency solutions, removing his initial motive for inventing it.

8. In 1929, Dirac interprets the negative-frequency solutions of his equation as negative-energy electrons, but uses the Pauli exclusion principle to argue that because electrons are fermions, this is okay as long as the negative-energy states are mostly filled. Dirac interprets the "holes" in the his negative-energy electron sea or Dirac sea to be positively charged particles with positive energy.

9. Since the only positively charged particles around are protons, Dirac argues that his holes are protons, even though his theory predicts they must have the same mass as the electron.

10. In 1931, Weyl convinces Dirac to come out and admit his theory predicts the existence of a new positively charged particle with the same mass as the electron, called the positron.

11. Researchers on cosmic rays notice that they had been seeing positrons for some time but ignoring them because everybody believed no such particle existed. The positron is now "discovered", by Carl Anderson in 1932, meaning recognized.

12. Quantum field theorists realize that the Klein-Gordon equation is actually a correct description of spin-0 particles, and that for a complex-valued field the negative-frequency solutions correspond to antiparticles, just as in the Dirac equation. Since spin-0 particles are bosons, the Pauli exclusion principle does not apply here, so Dirac's original argument involving "holes" cannot be used to explain why particles don't sink into negative-energy states.

13. Quantum field theorists gradually straighten everything out, slowly dropping the "hole" story.

14. Condensed matter theorists studying semiconductors find that positively charged carriers are actually "holes" giving an example where Dirac's idea is actually the best way to think about things. An electron and hole can form a bound state called an exciton.

There are three discrete symmetries that are commonly used in particle physics. Charge conjugation is when you replace every particle with its antiparticle. Parity inversion is if you hold up a mirror to the reaction, and look at its mirror image. Time reversal is if you run it backwards, analogous to filming it, and running the film backwards. This is how you would write down each of these symmetries.

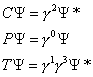
C [psi] = [gamma]² [psi]*

P [psi] = [gamma]⁰ [psi]

T[psi] = [gamma]¹ [gamma]³ [psi]*

C, P, and T are symmetry operators. If a reaction is symmetric under these operations, then if you perform these operations, you still get a valid reaction.

The motivated reader can choose to derive the above equations. For charge conjugation, you take the wavefunction for a negative energy electron.

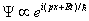
[psi] is proportional to e^{i(px + Et)/[h bar]}

and reverse the signs of p and E. Then swap ψ_U and ψ_D so that the negative energy states map onto part of the wavefunction that behaves correctly at low energies, and you also need a spin flip. It turns out that γ² will do that.

It used to be believed that all reactions obeyed C, P, and T symmetry. However, in 1956, it was proved that the weak force violated parity. It had previously been believed that parity was a conserved quantum number. Parity conservation was originally thought of by Eugene Wigner in 1927. According to this view, there were two particles, θ, which had even intrinsic parity, and τ, which had odd intrinsic parity.

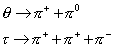
[theta] -> [pi]⁺ + [pi]⁰

[tau] -> [pi]⁺ + [pi]⁺ + [pi]^-

However, θ and τ had equal masses and lifetimes, and were identical in every way, so it seemed logical that they were one particle called K⁺, which meant parity is not conserved.

Remember

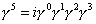
[gamma]⁵ = i[gamma]⁰[gamma]¹[gamma]²[gamma]³

This means that

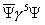
[psi bar] [gamma]⁵ [psi]

is a psuedoscalar that reverses sign under coordinate inversion.

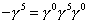
-[gamma]⁵ = [gamma]⁰ [gamma]⁵ [gamma]⁰

This means that parity will not be conserved. In October 1956, Lee and Yang suggested that parity was not conserved, and in December 1956, Wu and her team proved it using an experiment involving beta decay in cobalt-60. Chien Shiung Wu and her team worked with cobalt-60, which beta decays to nickel-60 with a half-life of 5.2 years. This is called a Gamow-Teller transition. The Co⁶⁰ nuclei had their spins aligned in a magnetic field. After the decay, the Ni⁶⁰ nuclei would have their spins aligned in the opposite sense, and this was checked by observing the spatial distribution of photons emitted in the subsequent gamma decays of Ni⁶⁰. Since the nuclear spin changes by one unit in the decay Co⁶⁰ → Ni⁶⁰ + e + [nu bar], then if L = 0, for the electron and antineutrino, their spins must point in the same direction to conserve angular momentum. If weak interactions conserved parity, half the time you would get a right-handed electron and left-handed antineutrino, and half the time, you would get a left-handed electron and right-handed antineutrino. Instead, you only get a left-handed electron, and right-handed antineutrino, which means that weak interactions do not conserve parity. It was realized that we only detect left-handed neutrinos and right-handed antineutrinos.

Then it was believed that all reactions obeyed C and P symmetry in combination, called CP, and also T. Then in 1963, it was realized from looking at kaon decay that CP symmetry was not always conserved. However, all reactions will obey CPT symmetry.

You can also discuss C, P, and T symmetry from the vantage point of group theory. A finite group is a group with a finite number of elements. One of the simplest groups has only two elements, the identity I, and an element g such that g² = e. Invariance under g is represented by the unitary operator.

[U, H] = 0

For a two element group, you have

U² = 1

since U is unitary, it is Hermitian. U is the observed quantity, and its eigenvalues are conserved quantum numbers.

U² | p> = p² | p>

where p is an eigenvalue of U corresponding to the eigenvector | p>. Since p² = 1, then the allowed eigenvalues of p are +1 and -1. Invariance of the system under symmetry operation g means that if the system is an eigenstate of U, then you can only go to states with the same eigenvalue. Here P and C are examples of the unitary operator U. Time reversal invariance requires an antiunitary operator.

{U, H} = 0