

e-R = PR [psi]e
e-L = PL [psi]e
The right-handed electron is placed in an SU(2) singlet. The left-handed electron and the electron neutrino, which is always left-handed, is placed in an SU(2) doublet.

Similarly, the left-handed up and down quarks are put in a doublet, while the right-handed up and down quarks are put in singlets.

Thus, the Standard Model Lagrangian is
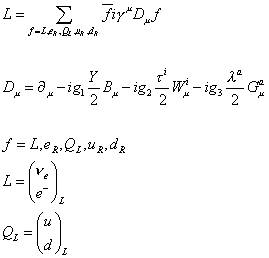
L = [summation, f = L, eR, QL, uR, dR] [f bar] i[gamma]u Du f
where Du = [partial derivative]u - ig1(Y/2)Bu - ig2([tau]i/2)Wui - ig3([lambda]a/2)Gua
f = L, eR, QL, uR, dR
L = ([nu]e e)L QL = (u, d)L
and where Y is the hypercharge, τi are the Pauli spin matrices, λa are the Gell-Mann matrices, and g1, g2, and g3 are coupling constants.
We say that the electromagnetic field Au is a combination of Bu and of Wu0 which are orthogonal normalized fields.

Au is proportional to g2 Bu - g1 YL Wu0
Au is orthogonal to another field Zu

Zu is proportional to g1 YL Bu + g2Wu0
Then Au and Zu are defined as follows.

Au = (g2Bu - g1YLWu0)/[squareroot of (g22 + g12YL2)]
Zu = (g1YLBu + g2Wu0)/[squareroot of (g22 + g12YL2)]
You can then solve for Bu and Wu0

Bu = (g2Au + g1YLZu)/[squareroot of (g22 + g12YL2)]
Wu0 = (-g1YLAu + g2Zu)/[squareroot of (g22 + g12YL2)]
I want to avoid algebra in this paper so I'll just give the results. You can also solve for e, the charge of the electron. You ultimately get

e = (g1g2)/[squareroot of g22 + g12]
You can then define

sin [theta]w = g1/[squareroot of g22 + g12]
cos [theta]w = g2/[squareroot of g22 + g12]
and thus

g2 = e/(sin [theta]w)
g1 = e/(sin [theta]w)
where θw is the Weinberg angle.

sin2 [theta]w ~ 0.23
So ultimately, you have the Wu fields which mix to create the W+ and W-. The Wu field combines with the Bu field in one way to create the electromagnetic field Au, and in another way to create the Z0.
Here are some numerical relations for the few GeV range and below.

GF/[squareroot of 2] = g22/8mW
g2 = e/sin [theta]w
g1 = e/cos [theta]w
[alpha] = e2/4[pi] = 1/137
[alpha]1 = g12/4[pi] = 1/100
[alpha]2 = g22/4[pi] = 1/30
[alpha]3 = g32/4[pi] = 0.1 - 0.3
This combination of electromagnetism and the weak force is called electroweak theory. It was first suggested by Sheldon Glashow in 1961. It was then elaborated by Steven Weinberg in 1967, and Abdus Salam in 1968. Glashow, Weinberg, and Salam shared the 1979 Nobel Prize for their work. Steven Weinberg's 1967 paper unifying electromagnetism and the weak force is the most frequently cited paper in Physical Review Letters. Weinberg and Salam added the concept of mass generation via the Higgs mechanism. The electroweak theory works fine except that it assumes the intermediate vector bosons were massless, which would cause the weak force to be a long range force, which it is not. If they were massive, it would be a short range force. How do you add mass without destroying the gauge invariance? This is accomplished by the Higgs mechanism.
The electroweak is a SU(2) x U(1) theory. The Lagrangian density of the boson is a sum of the U(1) gauge fields Bu, and the three SU(2) gauge fields Wui, where i = 1, 2, 3.

L = -(1/4) FBuv (x) FBuv - (1/4)FWuvi (x) FWiuv (x)
where

FBuv = [partial derivative]vB - [partial derivative]uB
FWiuv = [partial derivative]vWiu - [partial derivative]uWiv
The familiar fields are formed by

Au = cos [theta]w Bu = sin [theta]w Wu3
Zu = sin [theta]w Bu - cos [theta]w Wu3
W+ = 1/[squareroot of 2]/(Wu1 - iWu2)
W- = 1/[squareroot of 2]/(Wu1 + iWu2)
Now you could just include mass terms for the W+, W-, and Z0 particles but then it would no longer be invariant under U(1) gauge transformations.

[psi](x) -> [psi]'(x) = eiY[xi](x)[psi](x)
where Ψ is the boson field, Y is the hypercharge, and ξ(x) is any differentiable function.
The way you give mass to the W and Z bosons while keeping the gauge theory SU(2) x U(1) invariant is by spontaneous symmetry breaking.
The easiest way to describe this concept is with the Mexican hat potential. Let's say you had a system where the minimum energy was not at the origin. You could imagine a classical system with a small ball placed on top of a hill.

On top of the hill, the ball is at the origin, and the system is symmetric under rotations about the z-axis. However, it is unstable. The ball is not at minimum gravitational potential energy. Now, if the ball were to roll down the hill to the ring at the bottom, the system would no longer be symmetric under rotations about the z-axis. However, the ball would now be in a state of minimum gravitational potential energy. It's now in an energetically favorable position. This is spontaneous symmetry breaking at the classical level.
Another frequently cited example of spontaneous symmetry breaking involves ferromagnetism, but I think the above simple example is actually a better analogy for the Higgs mechanism.
Let's do a simple example before doing the Higgs mechanism. Let's say you have the following example.

L = [partial derivative]u [psi]* [partial derivative]u [psi] - V([psi])
where Ψ is a complex field

[psi] = ([squareroot of 2]/2) [[psi]1 + i[psi]2]
and V(Ψ) is the potential energy

V([psi]) = [mu]2 | [psi] |2 + [lambda] | [psi] |4
The constants μ2 and λ are real, with λ positive so it will be bounded from below. The Lagrangian is invariant under global U(1) transformation describing rotations in the complex plane. In order for the vacuum, the lowest energy state, to be invariant under Lorentz transformations and translations implies that Ψ (x) is a constant in the vacuum state.
If μ2 is positive, then the minimum potential energy is when Ψ = 0. If μ2 is negative, the minimum potential energy is a ring in the complex plane.

[psi] Vmin = [squareroot of -[mu]2/2[lambda]] ei[theta]
It doesn't make any difference what direction it goes in, so let's set θ = 0

[psi] Vmin = [squareroot of -[mu]2/2[lambda]]
Define ν such that

[psi] Vmin = [squareroot of -[mu]2/2[lambda]] = v/[squareroot of 2]
The deviation from the chosen minimum can be described in terms of the real fields σ and n defined by

[psi] = ([squareroot of 2]/2) [v + [sigma] + in]
The Lagrangian written in terms of σ and n is

L = (1/2) [partial derivative]u [sigma] [partial derivative]u - [lambda]v2[sigma]2 + (1/2)[partial derivative]un[partial derivative]un - [lambda]v[sigma][[sigma]2 - n2] - (1/4)[lambda][[sigma]2 + n2]2 + C
The higher terms are interaction terms so the free Lagrangian is

L = (1/2) [partial derivative]u [sigma] [partial derivative]u - [lambda]v2[sigma]2 + (1/2)[partial derivative]un[partial derivative]un
σ and n are two real Klein-Gordon fields. By quantizing these fields, the Lagrangian describes two different spin 0 particle fields. The σ bosons will have mass

m[sigma] = v[squareroot of 2[lambda]]
arising from the σ2 while the n bosons are massless due to the minimum being degenerate. The remaining terms are interactions among the σ and n through perturbation theory.
In this hypothetical example, the spontaneous symmetry breaking of the U(1) symmetry, caused by the degenerate energy minimum of the Lagrangian, created a perturbation theory with a massive scalar boson.
Next, I'll show the Higgs mechanism for a U(1) x SU(2) theory. You replace the normal derivative with the covariant derivative

Du = [partial derivative]u + iqAu
You add the Lagrangian of the free fields.

L = Du [psi]* Du [psi] - V([psi]) - (1/4)FuvFuv
This new Lagrangian is invariant under the U(1) gauge transformation.

[psi](x) -> [psi]'(x) = [psi](x)eiq[xi](x)
Au -> Au'(x) = Au(x) + [partial derivative]u [xi](x)
where ξ is any differentiable function. You continue the same way we did before, and express the Lagrangian in terms of the variables σ and n.

L = (1/2)[partial derivative]u[sigma][partial derivative]u[sigma] - [lambda]v2[sigma]2 + (1/2)[partial derivative]un[partial derivative]un -(1/4)FuvFuv + (1/2)q2v2AuAu + qvAu[partial derivative]un + higher terms
The Lagrangian has a massive vector boson field A and two scalar boson fields σ, n, with n massless. However, it also has the term

Au[partial derivative]un
There is no way to interpret this. It is not an interaction term since it is quadratic in the fields as if it were a free field. Therefore, we have to get rid of it. This Lagrangian has an extra degree of freedom that can be absorbed by doing a gauge transformation where

[psi](x) = ([squareroot of 2]/2) [v + [sigma](x)]
In this gauge, the n field disappears, leaving

L = (1/2)[partial derivative]u[sigma][partial derivative]u[sigma] - [lambda]v2[sigma]2 + (1/4)FuvFuv + (1/2)q2v2AuAu + higher terms
The way the Higgs mechanism works is that when you have symmetry breaking, the number of degrees of freedom doesn't change, but the particles change, so the degrees of freedom are redistributed into other particles. This only works if you have a degenerate vacuum.
Let's see how the numbers work out. A scalar particle has one degree of freedom. A complex scalar field has two degrees of freedom since a + bi has two components. A massless vector particle travels at the speed of light, so it only has two transverse polarized states, so that's two degrees of freedom. A massive vector particle also has a longitudinal polarized state, so that's three degrees of freedom.
In our first simple example of U(1) spontaneous symmetry breaking, before symmetry breaking, you had a complex scalar field (2 degrees of freedom), and a massless vector boson (2), so that's 2 + 2 = 4. After symmetry breaking, you had a scalar particle (1), and massive vector boson (3), so that's 1 + 3 = 4.
In the recent case of the U(1) x SU(2) Higgs mechanism, before symmetry breaking, you had a complex doublet (2 + 2 = 4), and four massless vector bosons (2 + 2 + 2 + 2 = 8). Therefore you had 4 + 8 = 12 degrees of freedom. After symmetry breaking, you had a scalar particle (1), a massless vector boson (2), and three massive vector bosons (3 + 3 + 3 = 9). Therefore you had 1 + 2 + 9 = 12 degrees of freedom.
The three massive vector bosons are the W+, W-, and Z0. The massless vector boson is the photon. The scalar particle is the Higgs particle.
Introducing the masses of the vector bosons with one complex doublet of complex scalars is the simplest scenario. An infinite number of such scalar fields can be added. The simplest supersymmetric models have five scalar fields left over after the Higgs mechanism. They are a doublet of charged scalars, two neutral scalars, and one neutral psuedoscalar.
The masses of the particles are given by

mW = (1/2)vg
mZ = mW/cos [theta]w
mH = [squareroot of 2[lambda]v]
where g is the weak coupling constant, and θw is the Weinberg angle. You can express mW and mZ through GF, α, and sin θw by using the following relations

v2 = [squareroot of 2]/2GF
[alpha] = (g2sin2[theta]w)/4[pi]
where GF is the Fermi constant, and α is the fine structure constant. You can measure the Fermi constant from the muon lifetime, and the Weinberg angle from the relative cross sections of the neutral current and charged current. It was therefore possible to predict the masses of the W+, W-, and Z0. In 1983, these three particles were detected with the expected masses in the UA1 and UA2 experiments at the CERN proton-antiproton synchrotron.
The vacuum expectation value is

v = 2mW/g = 246 GeV
We have no way of measuring λ so we have no way of calculating the Higgs mass. However, self-consistency sets an upper limit on the Higgs mass of 1 TeV. Right now, the search for the Higgs particle is the primary focus of experimental particle physics.
The Lagrangian for the electroweak and Higgs is divided into the following sections.
L = L0 + LFB + LFH + LBB + LBH + LHH
L0 is the Lagrangian of the free fields

L = [psi bar]f (i[partial derivative slash] - mf)[psi]f -(1/4)FuvFuv -(1/2)FuvdagFwuv +mW2Wu/dagWu -(1/4)FzuvFzuv + (1/2)mZ2ZuZu + (1/2)[partial derivative]u[sigma][partial derivative]u[sigma] - (1/2)mH2[sigma]2
LFB is the interaction between fermions and bosons, LFH between fermions and Higgs, LBB between bosons and bosons, LBH between bosons and Higgs, and LHH is the Higgs self-interaction.
Here is the fermion Higgs interaction term.

LFH = -(1/v)mf [psi bar]f [psi]f [sigma]
When a symmetry is spontaneously broken, you get a massless particle called the Nambu-Goldstone boson. Also called just a Goldstone boson, named after Jeffrey Goldstone, it is a massless boson resulting from a spontaneously broken global symmetry. Now, you might initially assume that the Higgs boson is such a particle but actually it is not. In field theories where local symmetries are spontaneously broken by the vacuum, the massless particles do not appear in the spectrum of physical states but rather provide longitudinal modes to the gauge bosons which become massive. Massless particles have just two transverse polarized states. When the W+, W-, and Z0 become massive, they gain a longitudinal state, which is actually the Goldstone boson associated with the symmetry breaking.
During symmetry breaking, the Hilbert space contains a physical subspace and an unphysical subspace. The Goldstone boson, and the massless gauge fermions, remain in the unphysical subspace, but their linear combination has extensions in the physical subspace, which is the resulting massive bosons.
The full name of the Higgs mechanism is actually the Brout-Englert-Higgs-Guralnik-Hagen-Kibble mechanism. Obviously, that's a cumbersome name, so they just name it after Peter Higgs.
Fermions can scatter by exchanging Higgs like other bosons but this is not considered a separate force because it does not have its own coupling constant, and is derived from the electroweak.
On 4 July 2012, the ATLAS and CMS experiments at CERN's Large Hadron Collider announced they had each observed a new particle in the mass region around 126 GeV. This particle is consistent with the Higgs boson predicted by the Standard Model. The Higgs boson, as proposed within the Standard Model, is the simplest manifestation of the Brout-Englert-Higgs mechanism. Other types of Higgs bosons are predicted by other theories that go beyond the Standard Model.
There is a major flaw with the Standard Model as described so far which I have not mentioned. According to the Standard Model Lagrangian previously given, all of the fermions are massless! Obviously, you can't just add mass terms since that would destroy gauge invariance. Luckily, the Higgs mechanism comes to the rescue. The Higgs mechanism does not give masses to the fermions the way it does for the W+, W-, and Z0, but the interaction between the fermion fields and the Higgs complex scalar field allows for fermion masses.
Let's say you have the following interaction Lagrangian for leptons. The second term is a Hermitian conjugate of the first.

Lint = ge ([L bar] [phi]eR + [phi] †[eR bar]L)
where the lepton doublet is

and the Higgs complex doublet is

The following equation is SU(2) invariant.

[L bar] [phi] = [nu bar]eL[phi] † + [eL bar][phi]0
Multiplying by the singlet e-R has no effect on SU(2) invariance. The coupling ge is arbitrary.
Now let's say spontaneous symmetry breaking takes place. Then you make the following substitution.

where v is the Higgs vacuum expectation value, and H is the remaining physical Higgs boson. You then get

Lint = (gev/[squareroot of 2])([eL bar]eR + [eR bar]eL) + (ge/[squareroot of 2])([eL bar]eR + [eR bar]eL)H
The first term in the Lagrangian can be identified with the fermion mass. You can then write the electron mass as

me = gev/[squareroot of 2]
Now, if it were possible to somehow measure ge experimentally, then the Standard Model would be able to actually calculate fermion masses similar to calculating the masses of the intermediate vector bosons. However, we have no idea how to do that, so instead the Standard Model simply allows for the existence of fermion masses without calculating them. The only way to get a value for ge is to measure the electron mass, and use that to calculate it.

ge = ([squareroot of 2]me)/v
The second term in the Lagrangian says there is an electron-electron-Higgs vertex of strength

ge/[squareroot of 2] = me/v

Rewriting the interaction Lagrangian to eliminate ge, you have

Lint = me [e bar]e + (me/v) [e bar]eH
For quarks, it proceeds as above, but with an additional element which didn't exist before since there is no νR.
In SU(2) spin theory, if

is an SU(2) doublet, then so is

Similarly, if

is an SU(2) doublet, then so is

which after spontaneous symmetry breaking, becomes

Since φ has hypercharge Y = +1, φ0 has Y = -1, and still satisfies Q = I3 + Y/2.
Then for quarks

Lint = gd[QL bar][phi]dR + gu[QL bar][phi]cuR + Hermitian conjugate
After going through algebra, you get

Lint = md[d bar]d + mu[u bar]u + (md/v)[d bar]dH + (mu/v)[u bar]uH
Thus, the theory allows for up and down masses but does not calculate them, since we have no way of knowing gu or gd. The last two terms are interaction terms between the down quark and the Higgs, and the up quark and the Higgs.
Like everything else in the Standard Model, the second and third generations of fermions are identical to the first except for the measured value of the masses. They are handled in the same way.
The above method for allowing masses for the fermions can not be used for the neutrinos since according to the Standard Model, there are no right-handed neutrinos, or at least they don't appear in the doublets. Therefore, for a long time, it was assumed that neutrinos were massless. Then in the late 1970's, there was some experimental evidence, which later turned out to be inaccurate, that neutrinos were massive, and it got people thinking about the idea. Since then, there has been a steady increase in the evidence to support the claim until today, it's assumed that neutrinos have a small mass. Here are some reasons to think so.
1. Just the pattern of the Standard Model. The fermions are massive, and the bosons are massless. You could make the claim that the intermediate vector bosons were originally massless, and later acquired a mass via the Higgs mechanism.
2. The Solar Neutrino Problem. We detect fewer electron neutrinos from the Sun than we should which can be explained by neutrino oscillation, where neutrinos of one type turn into neutrinos of another type. This is only possible if they have mass.
In 1969, Bruno Pontecorvo suggested that neutrinos might oscillate between the electron and muon flavor states. Oscillations can occur if the physical neutrinos are actually particles with different masses but not unique flavors. An electron neutrino can change into a muon neutrino or tau neutrino as they propagate because the mass components that made up that pure flavor get out of phase. The probability for neutrino oscillations are enhanced as neutrinos interact with first generation fermions while leaving the Sun. This effect of matter-enhanced neutrino oscillations is called the MSW effect, developed by Mikheyev, Smirnov, and Wolfenstein in 1985. The measurements at the Sudbury Neutrino Observatory showed that the neutrino flux produced in the beta decay reaction in the Sun contains a significant non-electron type component when measured on Earth. This measurement is strong indication for the oscillation of solar neutrinos. This is strong evidence that neutrinos have mass.
3. Dark Matter. Massive neutrinos could be a hot dark matter candidate to help explain dark matter.
4. Supernovae 1987A. The neutrinos from the supernovae arrived at Earth over an interval of time. If they were massless, they would all be traveling at the speed of light, and would arrive simultaneously.
Thus neutrinos are believed to have a small mass but they can't be given mass by the same method described above for the other fermions. One simple way to allow neutrino masses is to take the lepton doublet and the Higgs doublet to write the following Lagrangian.

L = ([lambda]/M)[psi]L C-1 [tau]2 [psi]L [phi] [tau]2 [tau][phi]
where M is a new mass scale with M >> mW. The presence of 1/M is to give the operator the correct dimension. After SU(2) x U(1) symmetry is broken, you get the following effective mass for the neutrino.

M[nu]e = (4mW2/g2M)[lambda]
Another method of generating neutrino masses is called the seesaw mechanism, and is realized in Grand Unified Theory models. The neutrino mass is a combination of the Dirac and Majorana forms.

The Dirac mass m is generated the same way as the lepton masses. The mass M is large enough to explain why right-handed neutrinos are not seen since M is of the order of the GUT mass. The seesaw mechanism predicts the scaling

m[nu]e : m[nu][mu] : m[nu][tau] = mu2 : mc2 : mt2
What I described earlier was the minimal Higgs model with a single complex doublet. The next simplest possibility is to imagine two Higgs doublets which can be used to solve the strong CP problem.

The W and Z boson masses receive a contribution from both vacuum expectation values.

mW = (g/2)[squareroot of v12 + v22]
In this case, there are three neutral Higgs bosons, a positive Higgs, and a negative Higgs that remain physical after spontaneous symmetry breaking.
This model has an extra chiral U(1) symmetry which is identified with the U(1)PQ symmetry which is one possible solution to the strong CP problem.
Before when I discussed QCD, I ignored one additional possible gauge-invariant contribution to the Lagrangian which takes the following form

L = (g2/16[pi]2) [theta] Tr Fuv [F tilde]uv
where the dual field tensor is

[F tilde]uv = (1/2)[epsilon]uv[alpha][beta]F[alpha][beta]
ε is a pseudotensor that changes sign under reflection. Therefore, the term causes CP violation.
The observed amount of CP violation is very small. From limits on a possible magnetic moment of the neutron, we have

| [theta] | < 10-9
We do observe CP-violation due to the weak force. Weak CP-violation is contained in phases of the elements of the KM-matrix. However, we do not observe the QCD induced CP-violation predicted by the Standard Model, and this is called the strong CP problem. In 1977, Roberto Peccei and Helen Quinn suggested a possible solution to the strong CP problem. They theorized a new symmetry called Peccei-Quinn symmetry. This is an axial version of a simple phase rotation.

q -> ei[beta][gamma]5q
[phi] -> e-2i[beta][phi]
The transformation of the Higgs field is needed to keep QCD invariant. The effect of breaking this symmetry is to add a term in the Lagrangian of the same form as the CP-violating term but in which θ is now the phase of φ. The breaking of the Peccei-Quinn symmetry, which is global, creates a Goldstone boson called the axion. Even though Goldstone bosons are normally massless, the axion can acquire a small mass. Therefore the axion is a prime candidate for cold dark matter.
There is an extra global chiral U(1) symmetry called U(1)PQ which is spontaneously broken. The axion arises as the pseudo-Nambu-Goldstone boson for the broken symmetry. It’s called "pseudo" because the U(1)PQ symmetry is anomalous. This is what causes it to have mass. It has both QCD and electromagnetic anomalies, so you get a coupling to two photons. An axion in a background magnetic field could convert to a photon. Axions could also carry energy away from stars, so this gives another constraint. Other constraints come from looking for reactions like K+ → π+ + axion. The original Peccei-Quinn model had the U(1)PQ breaking associated with electroweak symmetry breaking, and is ruled out experimentally. Now the interest is in invisible axion models where the U(1)PQ breaking scale is much higher. The axion mass equals λQCD{2}/f, where f is the PQ breaking scale, so invisible axions are very light. Current limits still leave the axion as a very good candidate for cold dark matter.