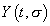
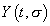
Y(t, [sigma])
which is the map from the string world sheet to the circle. T-duality exchanges Y for its world sheet dual [Y tilda]. Since Y is a world sheet scalar, [Y tilda] is a pseudoscalar.
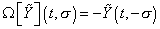
[omega] [[Y tilda]](t, [sigma]) = -[Y tilda](t, -[sigma])
Let [y tilda] be the constant in the mode expression of Y(σ), then
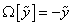
[omega][[y tilda]] = -[y tilda]
The gauging of world sheet parity means that a point on the circle with coordinate [y tilda] is identified with the point with coordinate -[y tilda] so the circle becomes an orbifold S1/Z2, where the Z2 action has two fixed points at
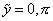
[y tilda] = 0, [pi]
Since S1/Z2 is just the closed interval
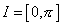
I = [0, [pi]]
the fixed points are actually 8-plane boundaries of the 9-dimensional space, called orientifold planes because the Z2 action on S1 is coupled with a change of orientation on the world sheet.
Therefore, the Type IA theory is effectively Type IIA theory compactified on the orbifold S1/Z2, which is like a circle containing a singularity because if you define one point on the circle to be the beginning, that point is also the end of the line segment. Closed strings that wind around the circle become open strings stretched between two 8-plane boundaries, each of which is associated with an SO(16) gauge group. Actually, the open strings in Type IA theory do not end on the 8-planes themselves but instead on 8-branes which coincide with them. Since a IIA superstring is a S1-wrapped supermembrane in d = 11 spacetime, the open strings of the IA theory must be wrapped d = 11 supermembranes stretched between two S1-wrapped 9-plane boundaries in d = 11 spacetime. Let L be the distance between these boundaries, and R be the radius of the circular dimension. Then you can identify Type IA theory as the R → 0 limit of M-theory compactified on a cylinder of radius R and length L. The stretched membrane is effectively wrapped on the cylinder, and has a closed string boundary on each of the two S1-wrapped 9-plane boundaries. Each string boundary must carry an SO(16) current algebra in order that an SO(16) gauge theory will emerge in the R → 0 limit.
Here you can draw the following moduli space.
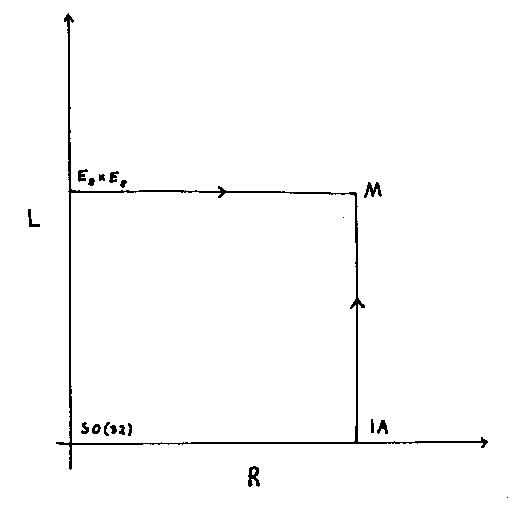
This shows the relation between Heterotic SO(32), Heterotic E8 x E8, Type IA string theory, and M-theory, where R is the radius of the cylinder, and L is the length of the cylinder. The moduli space of M-theory compactified on a cylinder includes all superstring theories with N = 1 supersymmetry. The generic vacuum of this moduli space is 11-dimensional, but you get a 10-dimensional theory with gauge group SO(32) in the limit where both the radius and the length of the cylinder go to zero, so the cylinder shrinks to zero area.
Let's look at open strings in Type IA theory. T-duality exchanges the Neumann boundary conditions on Y at the ends of an open string with Dirichlet boundary conditions on [Y tilda].
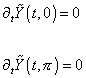
[partial derivative]t [Y tilda](t, 0) = 0
[partial derivative]t [Y tilda](t, [pi]) = 0
Therefore, the open strings must now start at some fixed value of [Y tilda], and end at some other, or the same, fixed value. For instance, open strings have their ends tethered to some number of parallel 8-branes. Unlike Neumann boundary conditions, Dirichlet boundary conditions do not prevent the flow of energy and momentum off the ends of the strings, so the 8-branes on which the strings end must be dynamical objects. They are called D-branes. The open strings end on D8-branes. The N = 2 supersymmetry of the IIB theory is broken to N = 1 in the Type I theory because of the restriction on the IIB fermion fields at the ends of open strings. The N = 2 supersymmetry of the IIA theory is also broken to N = 1 in the Type IA theory, but with the difference that since the ends of the open strings lie in the D8-branes, it is only on these branes that the N = 2 supersymmetry is broken. Everywhere else, you have the unbroken N = 2 supersymmetry of IIA theory. Thus, the Type IA theory is equivalent to the IIA theory on an interval with some number of D-branes.
The supersymmetry algebra implies a bound on the mass, for fixed charge, that is typically saturated. The state is then called BPS-saturated. BPS-saturated states preserve some fraction of the supersymmetry of the vacuum. The force between static BPS-saturated states vanishes so there also exist static BPS-saturated multi-soliton solutions. There is a generalization of this to Type II supergravity theories in which a multi-soliton is identified with a solution representing a number of parallel infinite planar p-branes. The central charge in the supersymmetry algebra becomes a p-form charge. Some of these p-branes, which all preserve half the d = 11 N = 2 supersymmetry, carry the charges associated with (p + 1)-form gauge potentials coming from the Ramond-Ramond, or R x R, sector of the Type II superstring theory. They are the R x R branes. There are R x R p-branes of IIA supergravity, for which p = 0, 2, 4, 6, and 8. There are R x R p-branes of IIB supergravity, for which p = 1, 3, 5, and 7. For p-branes in general, the long wavelength dynamics is determined by effective (p + 1)-dimensional field theory. For R x R branes, this world volume field theory includes a U(1) gauge potential. This is because the R x R branes of Type II supergravity theories are the field theory realization of the Type II superstring D-branes. This allows a string theory computation of the bosonic sector of the effective world volume field theory. The full action is then determined by supersymmetry and kappa symmetry. The result, upon partial gauge fixing, is a non-linear supersymmetric U(1) gauge theory of the Born-Infeld type, except that the fields now depend on the (p + 1) world volume coordinates of the brane.
Let's construct the M-theory superalgebra. This is similar to before when I constructed the GS action of superstring theory. If you like, you can reread the section on the GS formalism of superstrings. Let's first look at the d = 11 supermembrane. In d = 11, the minimal algebra is spanned by the 11-momentum PM, and a 32 component Majorana spinor of the d = 11 Lorentz group, Qα, obeying the anticommutation relation
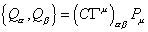
{Q[alpha], Q[beta]} = (C[capital gamma]u)[alpha][beta] Pu
where Q is a Majorana spinor, C is an antisymmetric real charge conjugation matrix, and Γu are the Dirac matrices. As before, you introduce the supertranslation invariant 11-vector-valued 1-form on the superspace
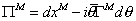
[capital pi]M = dxM - i[theta bar][capital gamma]Md[theta]
You next determine the super-Poincare invariant closed forms on the superspace. The only possibility is the 4-form
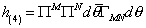
h(4) = [capital pi]M[capital pi]N d[theta bar][capital gamma]MN d[theta]
which leads to a membrane rather than a string. I'll use the word membrane to mean a 2-brane, although some people use it to mean any p-brane. The Nambu-Goto action has an obvious generalization to the p-brane case. The p = 2 case is sometimes called the Dirac action. The p = 2 Nambu-Goto action is
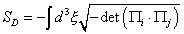
SD = -[integral] d3 [xi] [squareroot of -det([capital pi]i . [capital pi]j)]
There is a k-invariant supermembrane action of the form
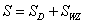
S = SD + SWZ
where SWZ is constructed from the 3-form b(3), where h(4) = db(3). Like before with the heterotic and type II superstrings, the WZ term modifies the supersymmetry algebra. Here you have
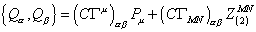
{Q[alpha], Q[beta]} = (C[capital gamma]M)[alpha][beta] PM + (C[capital gamma]MN)[alpha][beta] Z(2)MN
where Z(2) is a 2-form charge. You can take this d = 11 supertranslation algebra, and write it as a d = 10 algebra by splitting the charges into their representations under the d = 10 subgroup of the d = 11 Lorentz group. The d = 11 supersymmetry charge becomes a d = 10 Majorana spinor charge, and
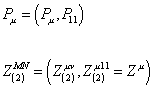
PM = (Pu, P11)
Z(2)MN = (Z(2)uv, Z(2)11 = Zu)
In this notation, the supersymmetry algebra can be written as
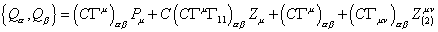
{Q[alpha], Q[beta]} = (C[capital gamma]u)[alpha][beta] P[alpha] (C[capital gamma]u)[alpha][beta] Zu + (C[capital gamma]11)[alpha][beta] + (C[capital gamma]uv)[alpha][beta] Z(2)uv
where Γ11 is the product of the Dirac matrices. Notice that not only do you have the 1-form charge Z associated with the IIA string, but you also have a 0-form charge P11, and a 2-form charge Z(2). This suggests not only that the IIA superstring is really a d = 11 supermembrane but that the non-perturbative d = 10 theory is a theory not just of strings but also 0-branes and 2-branes.
It turns out that a closed (p + 2)-form on superspace is necessary only if, after gauge-fixing the k-symmetry, the world volume fields consist only of scalars and spinors. While this is the case for p-brane solutions of flat space field theories, and for some p-brane solutions of supergravity theories, it is not true in general, which was originally discovered by an analysis of the small fluctuations about 5-brane solutions of type II supergravity theories. An example in d = 10 are D-branes, whose world volume field content is that of d = 10 vector multiplets dimensionally reduced to (p + 1) dimensions. Another example is the 5-brane solutions of d = 11 supergravity for which the field content is that of 6-dimensional antisymmetric tensor multiplet. These additional possibilities for p-branes in d = 10 and d = 11 supergravity theories are also associated with p-form extensions of the supersymmetry algebra. For instance, the d = 11 super-5-brane is associated with a 5-form extension of d = 11 supergravity algebra. Therefore, the full d = 11 supertranslation algebra is
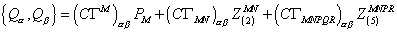
{Q[alpha], Q[beta]} = (C[capital gamma]M)[alpha][beta] PM + (C[capital gamma]MN)[alpha][beta] Z(2)MN + (C[capital gamma]MNPQR)[alpha][beta] Z(5)MNPQR
The three types of charge appears on the right-hand side are those associated with the supergraviton, the supermembrane, and the super-5-brane, which are the three components of M-theory. Therefore, this is the M-theory superalgebra.
Another question is why are some dimensions compactified and others not. In general relativity, the curvature of spacetime is determined by gravity. Since string theory incorporates general relativity, the geometry of spacetime is determined dynamically. This explains how in string theory, which includes gravity, some of the dimensions could be compactified. Gravitational interactions could cause the extra dimensions to be compactified. This was one of the original motivations for why John Schwarz first applied string theory to a possible theory of gravity, since the earlier hadronic theory of strings, which did not include gravity, did not have any explanation as to how or why the extra dimensions could be compactified. However, perhaps a more useful way of phrasing it is to say that gravitational interactions affect the curvature of spacetime in such a way as to prevent dimensions from being compactified. One possibility is that it is the interaction between strings or p-branes that keeps the dimensions from compactifying. Let's say right after the Big Bang, all the dimensions were non-compact. If all the 11 dimensions were non-compact, and the 10 spatial dimensions were as infinite as the three we're familiar with, then they would have so much extra room or degrees of freedom, that the strings or p-branes would usually just sail right past each other without interacting. This lack of interaction could cause the dimensions to compactify one by one until you are left with the three uncompactified spatial dimensions we're familiar with. At that point, there would be little enough room for them to move around in, that interactions would be frequent enough that no further spatial dimensions would compactify.
A related idea is to use the anthropic principle. Let's say in different parts of the Universe, you had different numbers of dimensions compactified. You could also imagine there being an infinite, or very large, number of universes, and they had different numbers of dimensions, or different numbers of dimensions compactified. If in a given universe, or part of the Universe, there were more than three uncompactified spatial dimensions, the strings or p-branes would usually sail right past each other without interacting. With such a low rate of interaction between particles, it's unlikely that you would have the large amount of very complex interactions necessary for life to arise. On the other hand, if there were only one or two spatial dimensions, there would be such little room that the particles would crowd each other out, which would make complex interactions more difficult. It is less likely you would have really complex reactions or really complex molecules like DNA. Therefore, you can logically argue that three is the optimum number of uncompactified spatial dimensions for life to arise. Also, planets could not be in stable orbits around stars in more than three spatial dimensions. Also, in more dimensions, there would be more electron-positron pairs surrounding an electron, and thus more charge screening, and so the electromagnetic coupling constant would be less. This is not to say that you couldn't have life with other numbers of uncompactified spatial dimensions, but it would be less likely. Thus, we aren't looking at a totally unbiased random sample of universes or parts of the Universe, since we're here to ask the question. Therefore, you can explain the number of uncompactified dimensions using anthropic arguments.
This is also similar to the Brandenberger-Vafa mechanism. Robert H. Brandenberger and Cumrun Vafa considered what would happen to a tiny universe which is compact in all directions and filled with strings, some of which wind around the compact dimensions. Since the energy of a massive string is roughly proportional to its length, the winding modes of the strings make it expensive to inflate a dimension with winding modes and hence it is natural to assume that dimensions with winding modes stay small, while the rest may expand. Initially all directions have winding modes. However, when a winding string hits another string that winds in the same dimension but in the opposite direction, they may interact and unwind. Using thermodynamics, you then assume that as long as the strings can interact freely they thermalize, which leads to a net zero winding. A one dimensional object is likely to meet another such object only in up to three spatial dimensions. In more spatial dimensions, the probability for winding annihilation decreases drastically. Therefore, thermalization is expected to only happen in three of the available dimensions, which then can grow large while the rest are kept small by winding strings. After branes were discovered/invented, they reconsidered it and extended it to a gas of arbitrary p-branes. This is easily done by noting that a p-brane is likely to meet another p-brane in up to 2p+1 dimensions. For p = 1, this reproduces the above argument. So with various p-branes, the BV mechanism gives rise to a hierarchy of smaller and larger dimensions.
Historically, an important milestone on the road towards M-theory was Seiberg-Witten theory, which opened the door to discussing superstrings non-perturbatively. Nathan Seiberg and Edward Witten did important work on N = 2 supersymmetry. It was followed by Hull and Townsend's work on heterotic type II string equivalence. The main result of Seiberg-Witten theory was that you could state the exact non-perturbative low energy effective Lagrangian of N = 2 supersymmetric Yang-Mills theory with gauge group SU(2). It contains the effective renormalized gauge coupling g, and the theta angle [theta].
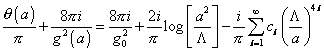
[theta]a/[pi] + 8[pi]i/g2(a) = 8[pi]i/g02 + 2i/[pi] log [a2/[capital lambda]2] - i/[pi] [summation over l from 1 to infinity] cl ([capital lambda]/a)4l
where Λ is the dynamically generated scale at which gauge coupling becomes strong, a is the Higgs field, g is the gauge coupling, cl is the instanton coefficients, and "l" is lower case L. The first term on the right-hand side is the bare value. The second term is the one loop effects. The third term is the instanton effects. The instanton effects is what causes non-perturbative effects. The difficulty in calculating non-perturbative effects is that you don't know the instanton coefficients cl. It was the achievement of Seiberg and Witten to determine all of the instanton coefficients cl explicitly. These coefficients give infinitely many predictions for zero momentum correlators involving a and gauginos in non-trivial instanton backgrounds. These correlators are topological. The fact that highly non-trivial mathematical results can be reproduced was striking evidence that Seiberg and Witten's approach was correct.
A recent development called Matrix theory, developed by Tom Banks among others, enables you to confirm many of the predictions of M-theory. You can prove the dualities and other relationships among the theories. Matrix theory is constructed in terms of N points, actually D0-branes, which exist in the 11-dimensional spacetime. The D0-brane is a BPS-state, and has a mass of
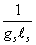
1/gsls
Their spatial positions are determined by the eigenvalues of nine N x N matrices, where N is eventually taken to infinity. The 10th dimension depends on N, the number of points. The 11th dimension lies on the light cone. Therefore, you only have nine dimensions left to be specified by matrix eigenvalues. So you see how you have reduced the number of dimensions you have to specify by one since the 10th dimension is determined by N. This is an example of a concept called the holographic principle where the physics of d-dimensional space, say 3d space, is determined by its (d - 1)-dimensional boundary, such as the 2d surface of 3d space. In this case, you can describe 10-dimensional space by only specifying nine dimensions. The light cone construction has its origin in the idea first thought of by Leonard Susskind and Gerard 't Hooft that the three-dimensional space in which we live can be completely described by its two-dimensional boundary because the third dimension is not independent of the other two dimensions. Tom Banks advocates the view that Matrix theory is in fact the fundamental M-theory. The construction has a generalization that describes compactification of M-theory on a torus, Tn. Although it's promising, there still remain problems with Matrix theory. It does not seem to work for n > 5. It treats the 11th dimension differently from the other dimensions.
Matrix theory is formulated in the light cone frame. It is constructed by building an infinite momentum frame, or IMF, boosted along a compact direction by starting from a frame with N unites of compactified momentum, and taking N to infinity. Lorentz invariance will arise, if at all, only in the large N limit. Therefore, Matrix theory is not background independent. A complete list of allowed backgrounds has not yet been found. Many properties of Matrix theory appear to be connected with noncommutative geometry. In the current formation of Matrix theory, gravity and geometry emerge in a very awkward fashion.
You take general ideas of holographic theories in the infinite momentum frame, and combine them with maximal supersymmetry, and you get a unique Lagrangian for the fundamental degrees of freedom in flat infinite 11-dimensional spacetime. The quantum theory based on this Lagrangian contains the Fock space of 11-dimensional supergravity, as well as metastable states representing large semiclassical membranes. Charles Thorne suggested an approach to nonperturbative string theory based on the idea of string bits. Light cone gauge string theory can be viewed as a parton model in the IMF along a compactified spacelike dimension whose partons or fundamental degrees of freedom, carry only the lowest allowed value of the longitudinal momentum. In perturbative string theory, this property follows from the fact that longitudinal momentum is the length of the string in the IMF. Susskind realized that this property of string theory suggested that string theory obeyed the holographic principle, which had been proposed by ‘t Hooft as the basis of a quantum theory of black holes. The ‘t Hooft-Susskind holographic principle states that the fundamental degrees of freedom of a consistent quantum theory including gravity must live on a (d – 2)-dimensional transverse slice of d-dimensional spacetime. This is equivalent to saying they carry only the lowest value of longitudinal momentum so that wavefunctions of composite states are described in terms of purely transverse coordinates. This requires supersymmetry in order to work.
You construct a holographic IMF theory by taking the limit of a theory with a finite number of degrees of freedom. The Super-Galilean algebra consists of transverse rotations, Jij, transverse boosts, Ki, and supergenerators. Aside from the rotational commutators, the Super-Galilean algebra has the following form.
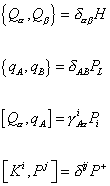
{Q[alpha], Q[beta]} = [delta][alpha][beta] H
{q[alpha], q[beta]} = [delta]AB PL
[Q[alpha], qA] = [gamma]A[alpha]i Pi
[Ki, Pj] = [delta]ij P+
Since there are 11 spacetime dimensions, there are 9 transverse dimensions. The 10th spatial direction is the longitudinal direction of the IMF. We imagine it to be compact, with radius R. The total longitudinal momentum is N/R. The Hamiltonian is the generator of translations in light cone time, which is the difference between the IMF energy, and the longitudinal momentum. The essential simplification of the IMF follows from thinking about the dispersion relations for particles.
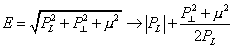
E = [squareroot of PL2 + P[perpendicular]2 + M2] -> | PL | + (P[perpendicular]2 + M2)/2 PL
The second form of this equation is exact in the IMF. It shows that particle states with negative or vanishing longitudinal momentum are eigenstates of the IMF Hamiltonian, E - PL, with infinite eigenvalues. You can then integrate them out, leaving a local in time Hamiltonian formulation of the dynamics of those degrees of freedom with positive longitudinal momenta.
The dynamical SUSY algebra is very difficult to satisfy. The known representations of it are all theories of free particles. To obtain interacting theories, you have to generalize the algebra to
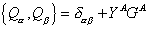
{Q[alpha], Q[beta]} = [delta][alpha][beta] + YA GA
where GA are generators of a gauge algebra which annihilate physical states.
If the degrees of freedom transform in the adjoint representation of the gauge group, the SUSY generators are linear in the canonical momenta of both Bose and Fermi variables, and there are no terms linear in the bosonic momenta of the Hamiltonian, then the unique representation of this algebra with a finite number of degrees of freedom is given by the dimensional reduction of the 9 + 1 dimensional SUSY Yang-Mills to 0 + 1 dimensions. The Super-Galilean symmetry, with kinematical SUSY generators is given by
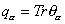
q[alpha] = Tr [theta][alpha]
where θα are the fermionic superpartners of the gauge field.
In order to have a Lagrangian where the number of the degrees of freedom is arbitrarily large, you can only have the groups U(N), O(N), or Sp(2N). However, the only one that is actually realized is U(N). The orthogonal and sympletic groups only appear in situations with reduced supersymmetry.
Duff, Hull, Townsend, and Witten established the existence of M-theory. Witten studied states that are charged under the Ramond-Ramond one-form gauge symmetry. The fundamental charged object is a D0-brane whose mass is
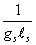
1/gsls
D0-branes are BPS states. If you assume the existence of a threshold bound state of N of these particles, and take into account the degeneracies implied by SUSY, you get a spectrum of states equivalent to that of 11d supergravity compacified on a circle of radius R = gsls.
If the Type IIA/M-theory duality is correct, the momentum in the tenth spatial dimension is identified with Ramond-Ramond charge, and is carried only by D0-branes and their bound states. If you take the D0-branes to be fundamental constituents, then they carry only the lowest unit of longitudinal momentum. In an arbitrary reference frame, you also have anti-D0-branes, but in the IMF, the only low energy degrees of freedom will be positively charged D0-branes. You go to the IMF by adding N D0-branes, and taking N to infinity.
One of the most important advances in superstring theory in recent years is Anti-de Sitter/Conformal Field Theory, or AdS/CFT correspondence, discovered by Juan Maldacena in 1997, and made more precise by Gubser, Klebanov, Polyankov, and independently by Witten, in 1998. This is an equivalence between superstring theory on certain ten-dimensional backgrounds involving Anti-de Sitter spacetime, and four-dimensional supersymmetric Yang-Mills theories. The AdS/CFT correspondence is very surprising because it relates a theory of gravity to a theory with no gravity at all, and no particles with spin > 1, and it relates highly non-perturbative problems in Yang-Mills theory to problems in classical superstring theory or supergravity. Also, it relates a ten-dimensional theory to a four-dimensional theory, so it involves the holographic principle. Aside from being surprising, it is also very useful. The reason this is useful is because a problem that is difficult on one side of the correspondence, might be easy to solve on the other side. Therefore, you can convert difficult problems into easy problems.
The AdS/CFT correspondence suggests an amazing equivalence between two seemingly unrelated theories. On the AdS side of the correspondence, you have 10-dimensional Type IIB superstring theory compactified on the product space of 5-dimensional Anti-de-Sitter space and a five-sphere, AdS5 x S5, where the Type IIB 5-form flux through S5 is an integer N, and the AdS5 and S5 have equal radii L given by
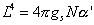
L4 = 4[pi]gsN[alpha]’
On the other side, the SYM side, of the correspondence, you have 4-dimensional supersymmetric Yang-Mills theory with maximal N = 4 supersymmetry, gauge group SU(N), and Yang-Mills coupling gYM2 = gs in the conformal phase. The AdS/CFT conjecture states that these two theories, including operator observables, states, correlation functions, and full dynamics are equivalent to each other.
In the strongest form of the conjecture, the correspondence is to hold for all values of N, and all regimes of coupling gs = gYM2. It’s also useful to look at certain limits of the conjecture. The ‘t Hooft limit of the SYM-side, in which
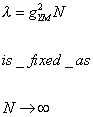
[lambda] = gYM2 N
is fixed as N → ∞ corresponds to classical string theory on AdS5 x S5, with no string loops on the AdS side. Therefore, classical string theory on AdS5 x S5 provides with a classical Lagrangian formulation of the large N dynamics of N = 4 SYM theory, called the masterfield equations. A further limit λ → ∞ reduces classical string theory to classical Type IIB supergravity on AdS5 x S5. Therefore, strong coupling dynamics in SYM theory, at least for the large N limit, is mapped onto classical low energy dynamics in supergravity and string theory, which is much easier to solve. You have a correspondence between a 10-dimensional theory of gravity, and a 4-dimensional theory with no gravity at all, and no particles with spin > 1.
The original correspondence by Juan Maldacena is between N = 4 SYM in its conformal phase, and string theory on AdS5 x S5. You can also use AdS6 x S4 or AdS4 x S6. The conjecture can also be adapted to situations without conformal invariance, and with little or no supersymmetry on the SYM side. The AdS5 x S5 spacetime is then replaced by some other manifold or orbifold solution to Type IIB, the study of which is usually more difficult.
Let’s say you have open strings attached to D3-branes. If there is one brane, their endpoints have to be on the same brane, and their length could go to zero, and they would be massless. If you have several parallel D3-branes, you could have strings with one endpoint on one brane, and the other endpoint on the other brane, and the minimum string length can’t go to zero, so they can’t be massless. In the limit where the distance between the branes goes to zero, so the branes are coincident, the length of the strings can then get arbitrarily small, and their mass would go to zero.
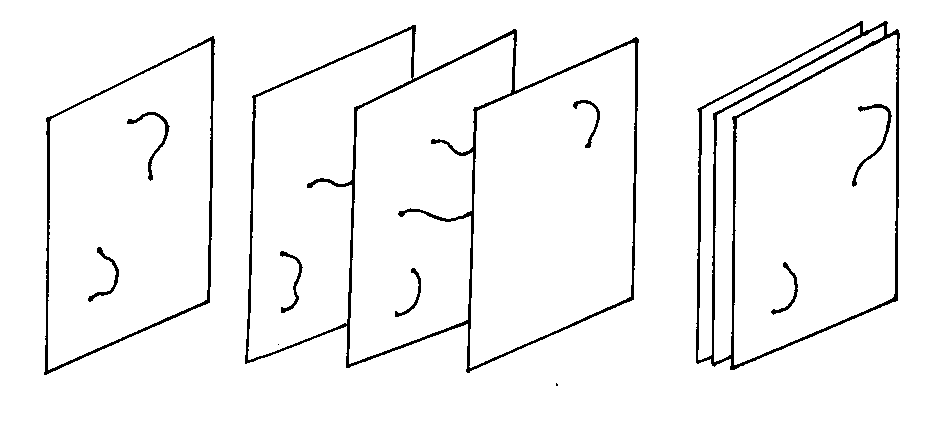
Open strings whose endpoints are attached to a single brane can have arbitrarily short length, and must therefore be massless. This excitation mode induces a massless U(1) gauge theory on the world brane, which is effectively 4-dimensional flat spacetime. Since the brane breaks half of the number of supersymmetries, it is ½ BPS. The U(1) gauge theory must have N = 4 Poincare supersymmetry. In the low energy approximation, which has at most two derivatives on bosons and one derivative on fermions, the N = 4 supersymmetric U(1) gauge theory is free.
With a number N > 1 of parallel separate D3-branes, the endpoints of the strings could be on different branes. There are N2 - N such possible strings. In the limit where the N branes tend to be coincident, all string states would be massless, and the U(1)N gauge symmetry is enhanced to a full U(N) gauge symmetry. Separating the branes is then interpreted as Higgsing the gauge theory to the Coulomb branch where the gauge symmetry is spontaneously broken.
The spacetime metric of N coincident D3-branes can be written as
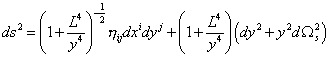
ds2 = (1 + L4/y4)-1/2 nij dxi dyj + (1 + L4/y4) (dy2 + y2 d[omega]s2)
where L is the radius of the D3-brane, and is given by
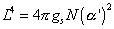
L4 = 4[pi]gs N([alpha]’)2
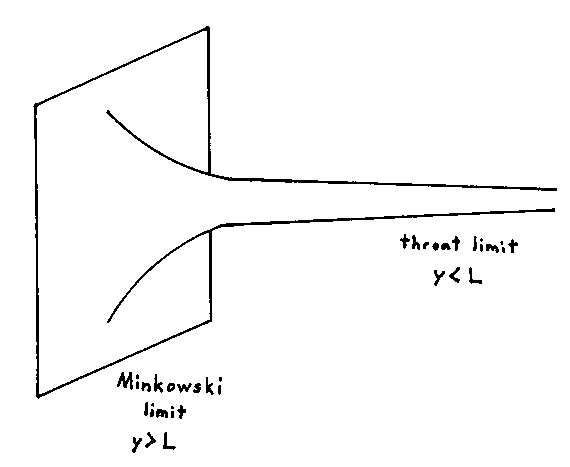
There are two regimes to look at. As y >> L, you get flat spacetime R10. When y < L, you get the throat, and it becomes singular as y << L.
With the redefinition
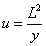
u = L2/y
and in the large u limit, the metric becomes
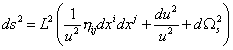
ds2 = L2 [1/u2 nij dxi dxj + du2/u2 + d[omega]s2)
which corresponds to a product geometry. One component is the five-sphere S5 with the metric
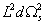
L2 d[omega]s2
The remaining component is the hyperbolic space AdS5 with the constant negative curvature metric.
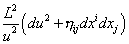
L2/u2 (du2 + nij dxi dxj)
Therefore, the geometry close to the brane, y = 0, or u = ∞, is regular and symmetrical, and may be summarized as AdS5 x S5, where both components have identical radius L.
The Maldacena limit corresponds to keeping gs and N fixed, as well as all physical length scales fixed, and letting α’ → 0. In the Maldacena limit, only the AdS5 x S5 region of the D3-brane geometry survives the limit, and contributes to the string dynamics of physical processes, while the dynamics in the asymptotically flat region decouples from the theory.
The AdS/CFT or Maldacena conjecture states the equivalence or duality between the following two theories.
1. Type IIB superstring theory on AdS5 x S5 where both AdS5 and S5 have the same radius L, where the 5-form Fs+ has the integer flux
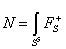
N = [integral over S5] Fs+
And where the string coupling is gs.
2. N = 4 supersymmetric Yang-Mills theory in 4 dimensions, with gauge group SU(N) and Yang-Mills coupling gYM in its superconformal phase.
with the following identifications between the parameters of both theories.
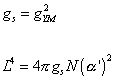
gs = gYM2
L4 = 4[pi]gs N([alpha]’)2
And the axion expectation value equals the SYM instanton angle < C > = θI. Equivalence includes a precise map between the states and fields on the superstring side, and the local gauge invariance operators on the N = 4 SYM side, as well as a correspondence between the correlators of both theories.
The ‘t Hooft limit consists of keeping the ‘t Hooft coupling
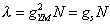
fixed, and letting N -> [infinity].
In Yang-Mills theory, this limit is well defined, at least in perturbation theory, and corresponds to a topological expansion of the field theory’s Feynman diagrams. On the AdS side, you can interpret the ‘t Hooft limit by saying that the string coupling constant can be expressed in terms of the ‘t Hooft coupling as
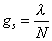
gs = [lambda]/N
Since λ is being kept fixed, the ‘t Hooft limit corresponds to weak coupling string perturbation theory.
After taking the ‘t Hooft limit, where λ = gs N is kept fixed while N → ∞, the only parameter left is λ. Quantum field theory corresponds to λ << 1. On the AdS side, it is natural to take λ >> 1 instead.
At the end of my paper on the Standard Model, I listed questions left unanswered by the Standard Model, and one of the questions was “Why is gravity so much weaker than the other forces?” Nothing that I’ve said so far addresses this question. However, this question is successfully addressed by a theory called the brane world scenario or brane world cosmology, the premise of which is that not all of the extra dimensions are compactified. Up until now, we have assumed that the reason we don’t detect the extra dimensions is because they are compactified on distance scales on the order of the Planck length. However, they would also not be detectable by us if all the fermions and gauge bosons were confined to a D3-brane within higher dimensional space. Remember, in Type I string theory, the fermions and gauge bosons are open strings, while the gravitons are closed strings. It’s easier to visualize with the following example. Let’s say that the open strings were all attached to a D2-brane, while the closed strings move freely throughout 3D space.
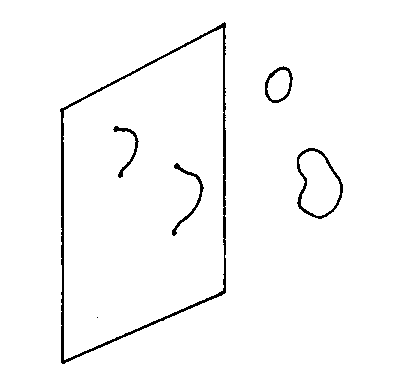
The fermions and gauge bosons, which are open strings, would be forced to slide around on a 2D plane, while the gravitons, which are closed strings, would have more room to move around, and would be floating around in 3D space. Therefore, the fermions and gauge bosons would interact with each other much more frequently than they would interact with the gravitons. Let’s say the fermions and gauge bosons were permanently attached to a D3-brane that is embedded within four spatial dimensions. From the point of view of the fermions and gauge bosons, the universe would appear to have three spatial dimensions, since they are confined to the D3-brane. However, the gravitons would have no such restriction, since they can move freely throughout the four spatial dimensions. You would then have an extra dimension which is not detectable by us even though it’s not compactified. Also, because the gravitons have the extra dimension to move around in, they would only rarely interact with the fermions and gauge bosons, which are stuck in three dimensions. The fermions and gauge bosons would interact with each other far more frequently than they would interact with the gravitons. Therefore, gravity would appear far weaker than the other forces. According to this theory, our entire Universe would be a giant D3-brane. Since, you’re assuming our world is a brane, this is called the brane world scenario or brane world cosmology. It assumes that our universe is a D3-brane, which has three spatial dimensions or four spacetime dimensions, and is embedded within a higher dimensional spacetime, which has four spatial dimensions or five spacetime dimensions. This higher dimensional spacetime is called the bulk, as opposed to our universe, which is called the brane. One version of the brane world scenario is called the Randall-Sundrum model, which assumes that our universe is one of two parallel D3-branes, and gravity originates on the other one.
The brane world scenario also provides an alternative explanation for the hierarchy problem. Quantum corrections to the Higgs mass would drive the Higgs mass up to the highest energy scale. If there were no physics beyond the Standard Model, it would only drive it up to the top quark mass, and there would be no problem. However, in grand unified theories, the Higgs mass would be driven up to the grand unification scale of 1016 GeV. More likely, there is some sort of theory of quantum gravity, and the Higgs mass would be driven up to the Planck scale of 1019 GeV. However, the Higgs mass can’t be higher than about 1 TeV without violating unitarity. The most common explanation for this is supersymmetry. Above the supersymmetry breaking scale, fermionic and bosonic contributions to the Higgs mass would cancel out, leaving a Higgs mass of about 1 TeV. However, the brane world scenario provides a different solution to this problem. Gravity appears weak to us only because we are confined to the brane, and within the bulk, gravity is not as weak as it appears to us. Therefore, gravity is not really as weak as it appears. Therefore, the Planck scale is not really as high as it appears. The weaker gravity, the higher the Planck scale would be. The stronger gravity, the lower the Planck scale would be. Due to the running of the coupling constants, the coupling constants converge, but the farther they are apart, the longer it would take for them to converge. Gravity is so much weaker than the other forces, it would only have the same strength as the other forces if you go all the way up to the Planck scale. However, if gravity is not really that weak, then the Planck scale is not really that high. The quantum corrections to the Higgs mass would drive it up to the highest energy scale, but if the real Planck scale is much lower than it appears to us, then that’s the highest energy scale, and the Higgs mass would only be driven up to that. The Higgs mass would be much lower, and you can solve the hierarchy problem. Therefore, in addition to providing an interesting explanation to the otherwise unanswered question of why gravity is so weak, the brane world scenario also provides an alternative explanation for the hierarchy problem. One thing that’s confusing is that some people use the phrase “hierarchy problem” to refer specifically to the question “Why is gravity so much weaker than the other forces?” which is a related but different question than the usual meaning of the phrase, which is how do you keep the Higgs mass low enough as to not violate unitarity.
In Heterotic E8 x E8 superstring theory, you have 10-dimensional spacetime, with 9 spatial dimensions, bounded by two 9-dimensional spacetime boundaries, each with 8 spatial dimensions. You then compactify it on a Calabi-Yau manifold, which has 6 dimensions, leaving 4-dimensional spacetime, with 3 spatial dimensions, bounded by two 3-dimensional spacetime boundaries, each with 2 spatial dimensions. In M-theory, there are 11 spacetime dimensions. Heterotic E8 x E8 superstring theory inspired Heterotic M-theory. You have 11-dimensional spacetime, with 10 spatial dimensions, bounded by two 10-dimensional spacetime boundaries, each with 9 spatial dimensions. You then compactify it on a Calabi-Yau manifold, which has 6 dimensions, leaving 5-dimensional spacetime, with 4 spatial dimensions, bounded by two 4-dimensional spacetime boundaries, each with 3 spatial dimensions. One of these can then be identified with our Universe, according to the brane world scenario. The more common way to compactify M-theory is to take 11-dimensional spacetime, with 10 spatial dimensions, and compactify it on a Joyce manifold, which has 7 dimensions, leaving 4-dimensional spacetime, with 3 spatial dimensions.
Fundamental particles are superstrings, which are D1-branes, and the Universe is a D3-brane. Therefore, “fundamental particle” and “Universe” are just different subcategories of the same type of thing, which are D-branes. There could be many D3-branes, each of which you could call a different universe, and they could act like fundamental particles. A D3-brane, and anti-D3-brane could be created from the vacuum, and then annihilate each other, analogous to an electron and positron being created from the vacuum, and then annihilating each other. A D3-brane and anti-D3-brane could form a bound state called branonium, analogous to an electron and positron forming a bound state called positronium. You have the unusual situation that our universe could be a fundamental particle in an atom in higher dimensional spacetime.
There is a long standing theory in cosmology that our universe has gone through an infinite number of cycles, where each Big Bang is preceded by a Big Crunch, and each Big Crunch is followed by a Big Bang. This is called cyclical cosmology, and it’s a small minority of cosmologists that ascribe to it. Brane world cosmology has inspired a version of cyclical cosmology, in which our universe is one of two parallel D-branes which are attracted to each other. When they impact, they bounce apart, and this is experienced as a Big Crunch/Big Bang on the D-branes. After they recoil, they are attracted to each other, and the process starts again. The main problem with this theory is that it has to pass through a singularity at each collision. The problem of the singularities is an endemic problem in all theories of cyclical cosmology.
Most cosmologists instead ascribe to inflationary cosmology. The original Big Bang model suffered from the flatness problem, the horizon problem, and the monopole problem. How can the Universe be as flat as the isotropy of the cosmic microwave background would seem to indicate? How can distant parts of the Universe that aren’t casually connected be so similar? Why haven’t we detected magnetic monopoles? All of these problems are solved by inflationary cosmology, which is assuming that the Universe went through a period of enormous inflation shortly after the Big Bang. During an internal of time on the order of the Planck time, a sphere with a radius of the Planck length would expand to several orders of magnitude larger than the current observable Universe. In conventional slow roll inflation, the Universe undergoes an expansion of a least 1026 during the inflationary phase. Such rapid expansion would flatten the Universe. Regions that were originally very close would become very distant but still remain similar. It’s very unlikely that any monopoles would end up in our observable Universe. Inflationary cosmology solves the flatness, horizon, and monopole problems. There is also experimental evidence for inflationary cosmology. The details of the cosmic microwave background as determined from COBE, Boomerang, Maxima, and most recently WMAP, provide overwhelming evidence for inflationary cosmology. The WMAP probe mapped the anisotropy of the cosmic microwave background to extraordinary precision, and the angular power spectrum of the temperature fluctuations in the cosmic microwave background were a very close match to the prediction from inflationary cosmology. In addition, from studying supernovae Ia, we can tell that the expansion of the Universe is accelerating, although obviously much less than it was originally. This all implies an effective positive cosmological constant, or some variation, such as quintessence, which is a rolling scalar field. This in turn requires de Sitter space, or something similar to it. De Sitter space can be defined as the maximally symmetric space with positive cosmological constant.
Empty de Sitter space is the unique spacetime with maximal symmetry and constant positive curvature. In D spacetime dimensions, it is locally characterized by
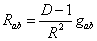
Rab = ((D – 1)/R2) gab
where R is the radius of curvature of de Sitter space, and by the vanishing of the Weyl tensor. The cosmological constant Λ is a function of R. With the local geometry fixed, the only remaining freedom is the global topology. You can think of de Sitter space as a timelike hyperboloid embedded in (D-1)-dimensional Minkowski space. The embedding equation is
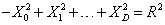
-X02 + X12 + …+XD2 = R2
where XI are Cartesian coordinates in Minkowski space. This makes the O(1, D) isometry group of de Sitter space obvious. O(1, D), the Lorentz group in D + 1 spacetime dimensions, has four disconnected components. These are the proper orthochronous Lorentz group, and its composition with the discrete symmetries P and T.
In de Sitter space, there is a problem in defining the S-matrix. In quantum field theory, asymptotic incoming and outgoing particles are properly defined only in the asymptotic region of spacetime. However, for de Sitter space, these regions are spacelike, and there is no single observer who can determine the states both at past infinity and future infinity. Therefore, the S-matrix elements in de Sitter space are not measurable quantities. They are metaobservables instead of observables. When you take into account quantum gravity in asymptotically de Sitter space, the problem becomes more severe. Witten pointed out that the only available pairing between in states and out states, CPT, is used to obtain an inner product for the Hilbert space. There does not seem to be an additional pairing between in and out states that could be used to arrive at an S-matrix. Since the conventional formulation of string theory is based on the existence of an S-matrix, this was a serious problem in trying to reconcile string theory with inflationary cosmology.
One attempt to make superstring theory consistent with inflationary cosmology was called pre-Big-Bang cosmology, which was based on trying to use the scalar fields already present in superstring theory to drive the inflation. This was only moderately successful. Another idea was to try to obtain de Sitter space from supergravity by reducing it on non-compact internal spaces, or by supergravity with negative norms. However, despite such valiant efforts, this appeared in to be such an intractable problem, that physicists talked about no-go theorems that supposedly proved that de Sitter space can’t be embedded into 11-dimensional supergravity.
It is therefore a great achievement, not to mention a relief, that recently, we have been able to expand M-theory to allow for de Sitter space. This is a very important result because we are finally unifying M-theory with inflationary cosmology. What you basically do is expand the moduli space of M-theory to include points that allow for de Sitter space. An example of this expanded M-theory is called MM-theory, developed by A. Chamblin and N. D. Lambert in 2002. Instead of using the standard spin connection D, they used a conformal spin connection
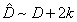
[D hat] ~ D + 2k
provided that the conformal part of the curvature vanishes. dk = 0 In simply connected spacetimes, this implies that k is exact, and the modification is simply a field redefinition. If k = dθ, then the redefinition that takes the equations of motion defined with the connection [D hat] back to the usual ones
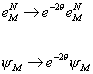
eMN -> e-2[theta] eMN
[psi]u -> e-2[theta] [psi]u
where M, N = 0, 1,…10. However, if the spacetime is non-simply connected, then this modification is non-trivial.
Let’s compactify MM-theory on M10 x S1. You can then choose k = m dy, where dy is the tangent vector to the circle. If you turn off the four-form field strength and the fermions, then the equations of motion of the compactified theory in 10 dimensions are
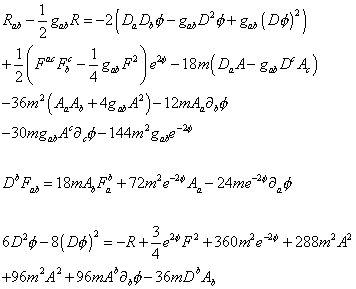
Rab - ½ gab R = -2(Da Db [phi] – gab D2 [phi] + gab + gab (D[phi])2) + ½ (Fac Fbc - ¼ gab F2) e2[phi] - 18m(Da Ab - gab Dc Ac) – 36 m2 (Aa Ab + 4 gab A2) – 12 m Aa[partial derivative]b [phi] – 30mgab Ac [partial derivative]c [phi] – 144m2 gab e-2[phi]
Db Fab = 18m AbFab + 72 m2e-2[phi]Aa -24me-2[phi] [partial derivative]a [phi]
6D2 [phi] – 8(D[phi])2 = -R + ¾ e2[phi] F2 + 360m2 e-2[phi] + 288m2 A2 + 96m2 A2 + 96mAb [partial derivative]b [phi] – 36mDb Ab
If you turn off all the gauge potentials, you are left with Einstein equation
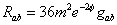
Rab = 36m2 e-2[phi] gab
Together with the Maxwell and scalar equations which imply that the dilaton φ is a constant. Therefore, if you turn off all of the fields except gravity, you get 10-dimensional de Sitter space. The effective cosmological constant is
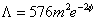
[capital lambda] = 576 m2 e-2[phi]
It now appears that within the entire moduli space of M-theory, or perhaps an expanded version of M-theory, there are points that allow for de Sitter space. M-theory then allows for inflationary cosmology. You could even say that we have achieved unification between the most advanced theoretical particle physics and cosmology. In inflationary cosmology, there are an infinite number of tiny regions of the early Universe that expanded to be larger than the observable Universe today. Since they are no longer casually connected, you could think of them as different universes. In eternal inflation, this has been going on for an infinite length of time. There are then an infinite number of universes, each of which corresponds to a different point in the moduli space of M-theory, and therefore, end up with different forces, particles, etc. The one we are in would then be selected using the anthropic principle. This seems to be a basically self-consistent description of the Universe that encompasses all of physics, and is the majority view among physicists. This is currently our basic view of the Universe.
However, Leonard Susskind gave a talk at a cosmology conference in Davis in March 2003, where he explained why we should temper our enthusiasm. It’s very probable that there is some point in the moduli space of M-theory that corresponds to the real Universe, but very unlikely that we will ever identify it. There are an infinite number of points in the moduli space of M-theory. There are thousands of free parameters, such as the precise details of the topology, the compactification, the wrapping modes of branes, fluxes, etc. Susskind called this vast parameter space encompassing all the possible values of all the possible free parameters, the landscape. Susskind estimates there are 10500 string vacua. It’s very unlikely that we’ll ever identify the precise point in the infinite moduli space of M-theory that corresponds to the real Universe. We don’t know which point it is, but we know which points it’s not, namely it’s none of the points we know about. Specifically, none of the five superstring theories which we’ve studied so exhaustively correspond to the real Universe since they don’t allow for de Sitter space. Therefore, at least for the foreseeable future, it looks like we’ll have to give up on the longstanding hope of using superstring theory or M-theory to actually calculate the parameters of the Standard Model or extensions of the Standard Model, much less shed new light on quantum gravity.
It appears that the octonions are relevant to M-theory. Therefore, to understand M-theory at a deeper level, you should study the octonions. For an excellent review of the octonions, read John Baez’s paper “The Octonions”.
A division algebra is an algebra for which if ab = 0, then either a = 0, b = 0, or a = b = 0. There are four normed division algebras which are the real numbers, complex numbers, quaternions, and octonions.
The real numbers R are a one-dimensional algebra that can be placed in order.
a
The complex numbers C are a two-dimensional algebra that have no order but are commutative and associative.
a + bi
where i2 = -1
The quaternions H are a four-dimensional algebra that are not commutative but are associative.
a + bi + cj + dk
where i2 = j2 = k2 = ijk = -1
In other words, the quaternions H are a four-dimensional algebra with basis 1, i, j, k where
1 is the multiplicative identity
i, j, k are the squareroot of –1
ij = k, ji = -k, and all identities obtained from these by cyclic permutations of (i, j, k)
Quaternions were invented by William Rowan Hamilton in 1843.
The octonions O are an eight-dimensional algebra that are not associative but are alternative, which is a weaker form of associativity. The octonions O are an eight-dimensional algebra with basis 1, e1, e2,…e7 where
1 is the multiplicative identity
e1, e2,…e7 are the squareroot of –1
Their multiplicative rules are summed up by a diagram called the Fano plane. If you multiply two numbers on a line, their product is the third number on that line. If you have to go in the opposite direction as the arrows, you add a minus sign to he next number on the line.
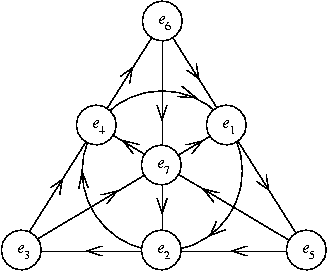
Octonians were invented by John T. Graves in 1844. For more information on octonions, read John Baez’s paper. M-theory displays geometric and algebraic structures derived from the octonions. The octonions are related to the exceptional Lie groups, G2, F4, E6, E7, and E8. Compact manifolds of G2 holonomy called Joyce manifolds, discovered in 1996, play a fundamental role in compactifying M-theory. The four coincidences in the list of simple Lie groups are
A1 = B1 = C1
SU(2) = Spin(3) = Sp(1)
B2 = C2
Spin(5) = Sp(2)
A3 = D3
SU(4) = Spin(6)
D2 = A1 x A1
Spin(4) = SU(2) x SU(2)
Are related to some irreducible representations of the exceptional Lie groups. They also appear in physics such as compactifications of M-theory disguised in various forms.
The four lists of classical supersymmetric p-branes, including instantons, embedded in D-dimensional spacetime correspond to the four normed division algebras R, C, H, and O.
Real ladder: From D = 1, p = -1 instanton (kink) to D = 4, p = 2 membrane (domain wall, codimension one)
Complex ladder: From D = 2, p = -1 instanton (vortex) to D = 6, p = 3 universe (codimension two)
Quaternionic ladder: From D = 4, p = -1 instanton to D = 10, p = 5 5-brane (codimension four)
Octonionic ladder: From D = 8, p = -1 Fubini-Nicola instanton to D = 11, p = 2 M2-brane
These four ladders can be thought of as oxidation of the corresponding instanton in its turn associated to the fundamental line bundle for the projective spaces KP1, where K = R, C, H, and O. The four are supersymmetrizable, and are linked as the four Hopf bundles. The Cayley plane OP2 is related to the 11d supergravity corner of M-theory.
Compactifying 11d supergravity from the original 11d to 4d causes all of the E series split forms to appear successively. The moduli spaces of scalar fields are homogenous spaces. The Heterotic E8 x E8 superstring theory makes direct use of E8 x E8. Also E6 appears in the compactification of E8 x E8.
In 10d superstring theory, it was common to compactify the extra dimensions on Ricci-flat Calabi-Yau manifolds. In 11d M-theory, it’s common to compactify the extra dimensions on G2-manifolds called Joyce manifolds, discovered in 1996. G2 compact holonomy manifolds are still Ricci-flat, and conserve 32/4 = 4 supercharges, which gives N = 1 supersymmetry in 4 dimensions. From the reduction of the tangent bundle of a compactifying space K7, you get
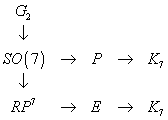
G2 holonomy involves some torsion properties in K7. The reason for the descent SO(7) to G2 is because the later conserves a 3-form related to the octonionic product, and probably related to the 3-form in M-theory in the 11d supergravity limit.
In 1914, Elie Cartan noticed that the smallest of the exceptional Lie groups, G2, is the automorphism group of the octonions. Its Lie algebra g2 is therefore der(O), the derivation of the octonions. G2 is the subgroup of Spin(7) fixing the unit vector in S7. Since Spin(7) acts trivially on the unit sphere S7 in this spinor representation, you have
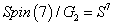
Spin(7)/G2 = S7
Both Im(H) and Im(O) are equipped with a 3-form, or an alternating trilinear function, given by
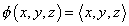
[phi](x, y, z) = x, y, z
In the case of Im(H), this is just the usual volume form, and the group of real linear transformations preserving it is SL(3, R). In the case of Im(O), the real linear transformation preserving φ are those in the group G2. The 3-form φ is important in Joyce manifolds, which are 7-dimensional Riemannian manifolds with holonomy group equal to G2.
The following equation is actually a pun.
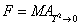
F = MAT2 -> 0
This proves that M-theorists have a sense of humor, albeit an esoteric one, as can be expected. This is the Aspinwall-Schwarz equation which describes how a general compactification of F-theory arises from M-theory. M-theory is compactified on an elliptically fibered manifold X, and the area of the fibers is then scaled to zero. However, any physics student who sees the above equation would be instantly reminded of Newton’s Second Law, F = ma, which is probably the second most famous equation in physics, second only to E = mc2. Perhaps one person out of a hundred would recognize Newton’s Second Law, but only one physicist out of a thousand would recognize the Aspinwall-Schwarz equation, so this is very much an inside joke.
D-branes have been used to calculate the entropy of black holes. Strominger and Vafa have shown that D-brane techniques can be used to count the quantum microstates associated with classical black hole configurations. The simplest case, which was studied first, is static extremal black holes in five dimensions. Strominger and Vafa showed that for large values of the charges, the entropy, defined by S = log N, where N is the number of quantum microstates that the system can be in, agrees with the Bekenstein-Hawking prediction of ¼ of the area of the event horizon. This result has been generalized to black holes that are near extremal and radiate correctly, or rotating.
D-branes are surfaces on which open strings can end. Their dynamics are described by open string theory, as described by Witten. However, this can be difficult to work with in practice, so it is sometimes useful to consider the low energy effective action obtained by integrating out all the massive modes, keeping only the massless super-Maxwell multiplet. This becomes practical only if you keep terms in which the fields are slowly varying at the string scale, keeping the field strengths but not their derivatives. The field strengths are allowed to be large but they can’t exceed a certain critical value. At this value, the stretching force on a string with charges on its ends matches the string tension. In the case of Type II superstrings, the effective action is the sum of two terms, a Dirac-Born-Infeld term and a Chern-Simons term.
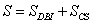
S = SDBI + SCS
The following versions of superstring theory are the most successful in terms of reproducing the particle spectrum from the Standard Model.
1. The most conventional one is E8 x E8 Heterotic superstring theory which was invented in 1985 by Gross, Rohm, Harvey, and Martinec. It has 10 spacetime dimensions, six of which are compactified on a six-dimensional Calabi-Yau space ,also called Calabi-Yau three-fold, where 3 is the complex dimension. This realistic compactification was discovered by Strominger, Witten, Candelas, and Horowitz. In the realistic models, one of the E8 gauge groups is broken to E6 to SO(10) to SU(5), which is subsequently broken to the Standard Model's SU(3) x SU(2) x U(1). Usually we are looking for the N=1 supersymmetric extensions of these theories, assuming that SUSY is broken spontaneously. You get the correct spectrum of gauge bosons as well as fermions, with the right-handed neutrino included, and some extra fermions that complete the 27 representation of E6. You can also calculate the number of generations, which you can arrange to be three.
2. If the model above has a coupling constant that is stabilized around a large value, a new 11th dimension of M-theory emerges. Because you started with the Heterotic theory, the new 11th dimension will have two boundaries, each of them carrying a single gauge group E8, which was found by Horava and Witten. The theory is called Heterotic M-theory or Horava-Witten theory. This extra 11th dimension can be in fact much larger than the 6 dimensions of the Calabi-Yau space, and therefore the world would appear as five-dimensional.
3. M-theory, the 11-dimensional theory, can also be directly compactified on 7-dimensional manifolds. They must have a G2 holonomy to get N=1 supersymmetry in four dimensions, and they must contain a singularity if we want to reproduce the spectrum of chiral fermions. Interesting calculations in these models exist, such as proton decay, and this model is in some sense the most geometrical one, because all the extra stringy degrees of freedom beyond the visible 4 dimensions are treated geometrically.
4. F-theory, invented by Cumrun Vafa in 1995, is formally a 12-dimensional theory, but you must always compactify two of its dimensions on a two-torus, which effectively leads to type IIB string theory. F-theory on a (d + 2)-dimensional manifold M is a fancy way to describe a compactification of Type IIB strings on a d-dimensional manifold which is the base of the (d + 2)-dimensional manifold M. The fiber must be a two-torus. The shape of the two-torus determines the complex coupling constant of type IIB string theory. F-theory on eliptically fibered, where the fiber is a two-torus, Calabi-Yau four-folds, which are eight-dimensional, is a realistic theory because it leads to N=1 supersymmetry in four dimensions. Randall-Sundrum models have been constructed using these models.
5. Intersecting brane models often construct non-supersymmetric Standard Models with essentially the right spectrum. These particles are vibrating strings whose two ends are attached to different D-branes that intersect. Various particles are therefore forced to be localized at different intersections. These models can again be realistic, and they naturally lead to hierarchy of fermionic masses.
Fluxes are generalizations of the magnetic flux, and are being added to the previous models, and it leads to new useful physical features.
I have described superstring theory which is our main way of trying to quantize gravity. However, there do exist alternative theories of quantum gravity, at least one of which is worthy of mention, called loop quantum gravity. This is a radically different way of trying to approach the problem of a quantum theory of gravity. It actually has nothing to do with particle physics, and is instead derived from general relativity. Particle physicists view general relativity in the same way they do Newtonian mechanics. We use classical Newtonian mechanics all the time to solve practical problems, and for most purposes, it’s sufficient, but it’s obviously not true since it does not take into account relativity or quantum mechanics. Fermi’s theory of the weak force is adequate for many applications, although it’s obviously not true since it’s non-renormalizable and has no mediating particle, and is only a sufficient approximation in the low energy limit. Particle physicists view general relativity in the same way. They consider it a useful tool that we use all the time, but to them, it’s obviously untrue at a fundamental level. First of all, it doesn’t include quantum mechanics. Second of all, it describes gravity in a radically different way from the other forces, and from what particle physicists are used to. In particle physics, the four forces are caused by the exchange of virtual bosons, which in the case of gravity is the graviton. In general relativity, gravity is the curvature of spacetime itself. In general relativity, there is no such thing as a graviton. This is a fundamentally different way of thinking about gravity. According to general relativity, what we call gravity is actually the curvature of spacetime.
There are far more particle physicists then general relativists, so the particle physics view is the majority view. However, general relativists do exist, and these people take the general relativity view seriously. Even they admit that general relativity in the form Einstein invented can’t be true because it doesn’t include quantum mechanics. However, their solution is to come up with a quantum version of general relativity. They have had some success, and this quantum version of general relativity is called loop quantum gravity. It retains the general relativity assumption that gravity is literally the curvature of spacetime, instead of the exchange of a particle, so therefore quantizing gravity means you are somehow quantizing the curvature of spacetime. Normally, the curvature of spacetime is considered the background metric, except here, it’s the thing being quantized, so that means there is no background metric. This shows you what an unusual theory this is because this is probably the only field of physics where there is no background metric at all. This requires radically different mathematics than anything else in physics. From the point of view of loop quantum gravity theorists, the absence of a background metric is an additional benefit to the theory. They believe the real Universe doesn’t have a background metric, and so preferably, you should do physics without it. Loop quantum gravity makes absolutely no attempt to try to unify gravity with the other forces. Rather, what they are trying to unify is what they perceive to be the two fundamental theories left to be unified, which are general relativity and quantum mechanics.
Loop quantum gravity began in the middle of the 1980’s. The pioneers of the field include Amitaba Sen, Abhay Ashtekar, Ted Jacobson, Lee Smolin, and Carlo Rovelli. A more recent offshoot of loop quantum gravity is called spin foam theory. The mathematical tools for dealing with nonperturbative loop quantum gravity include Penrose's spin network theory, SU(2) representation theory, Kauffman tangle theoretical recoupling theory, Temperley-Lieb algebras, Gelfand's C* algebra spectral representation theory, infinite dimensional measure theory, and differential geometry over infinite dimensional spaces.
With loop quantum gravity, you start with classical general relativity, which can be formulated as follows. You fix a three-dimensional manifold M, and consider a smooth real SU(2) connection Aai (x) and vector density
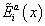
[E tilda]ia (x) transforming in the vector representation of SU(2) on M, where a, b,…=1, 2, 3 for spatial indices, and i, j, …=1, 2, 3 for internal indices. The internal indices can be viewed as labeling a basis in the Lie algebra of SU(2), or in the three axis of a local triad. You indicate coordinates on M with x. The relation between these fields and conventional metric variables is as follows. [E tilda]ia (x) is the inverse triad related to the three-dimensional metric gab (x) of the constant time surfaces by
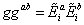
ggab = [E tilda]ia [E tilda]ib
where g is the determinant of gab and
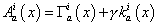
Aai (x) = [capital gamma]ai (x) + [gamma] kai (x)
where Γai (x) is the spin connection associated with the triad defined by
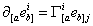
[partial derivative][aeb]i = [capital gamma][ai eb]j
where eaj is the triad, kai (x) is the extrinsic curvature of the constant time three surface.
γ is a constant called the Immirzi parameter. Different choices for γ give different versions of the formalism that are equivalent in the classical domain. If you choose γ to be equal to i.
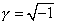
[gamma] = [squareroot of –1]
then A is the standard Ashtekar connection, which can be shown to be the projection of the self-dual part of the four-dimensional spin connection on the constant time surface. If you choose γ = 1, you get the real Barbero connection. The Hamiltonian constraint of Lorentzian general relativity has a simple form in the
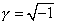
[gamma] = [squareroot of –1]
formalism. The Hamiltonian constraint of Euclidean general relativity has a simple form in the γ = 1 formalism. You can also choose other values of γ. It’s possible that quantum theory based on different choices of γ are inequivalent. There appears to be a unique choice of γ that gives the correct ¼ coefficient in the Bekenstein-Hawking formula.
The spinor version of the Ashtekar variables is given in terms of the Pauli spin matrices σi, where i = 1, 2, 3, or the SU(2) generators
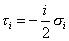
[tau]i = -i/2[sigma]i
by
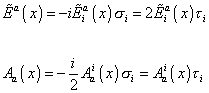
[E tilda] (x) = -i[E tilda]ia (x) [sigma]i = 2[E tilda]ia (x) [tau]i
Aa (x) = -i/2 Aai (x) [sigma]i = Aai (x) [tau]i
Thus Aa (x) and [E tilda]a (x) are 2 x 2 anti-hermitian complex matrices.
The theory is invariant under local SU(2) gauge transformations, three-dimensional diffeomorphisms of the manifold on which fields are defined, as well as under coordinate time translations generated by the Hamiltonian constraint. The full dynamical content of general relativity is captured by the three constraints that generate these gauge invariances.
The Lorentzian Hamiltonian does not have a simple form if you use the real connection. For a long time, this was considered problem in terms of using the real connection to define the quantum Hamiltonian constraint. Therefore, they used the imaginary constraint. However, Thiemann figured out how to construct a Lorentzian quantum Hamiltonian constraint, despite the non-polynomiality of the classical expression. Therefore, today, the real connection is widely used. This has the advantage of eliminating the old reality conditions problem, which was the problem of implementing non-trivial reality conditions in the quantum theory.
You use the trace of the holonomy of the connection, which is labeled by loops on the three manifold, and higher order loop variables, obtained by inserting the E field, in n distinct points, into the holonomy trace. Given a loop a in M, with points s1, s2,…sn in a, you have
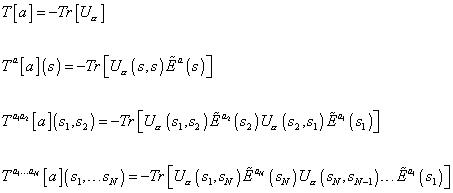
T[a] = -Tr[U[alpha]
Ta[a] (s) = -Tr[U[alpha] (s, s) [E tilda]a (s)]
Ta1a2[a] (s1, s2) = -Tr[U[alpha] (s1, s2) [E tilda]a2 (s2) U[alpha] (s2, s1) [E tilda]a1 (s1)]
Ta1…aN[a] (s1, …sN) = -Tr[U[alpha] (s1, sN) [E tilda]a2 (sN) U[alpha] (sN, sN - 1)… [E tilda]a1 (s1)]
where
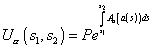
U[alpha] (s1, s2) = Pe[integral from s1 to s2] Aa (a(s))ds
in the parallel propagator of Aa along a defined by
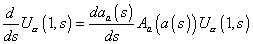
d/ds U[alpha] (1, s) = (daa (s))/ds Aa (a(s)) U[alpha] (1, s)
These are called the loop observables. The loop observables coordinatize the phase space, and have a closed Poisson algebra, denoted by the loop algebra. The Poisson bracket between
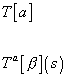
T[a] and Tc[beta] (s)
Is non-vanishing only if β (s) lies over a. If it does, the result is proportional to the holonomy of the Wilson loops obtained by joining a and β and their intersection.
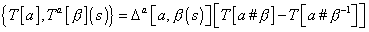
{T[a], Ta[beta] (s)} = [triangle]a [a, [beta] (s)] [T[a # [beta]] – T[a # [beta]-1]
where
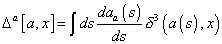
[triangle]a [a, x] = [integral] ds (daa (s))/ds [delta]3 (a(s), x)
is a vector distribution with support on a, and a # β is the loop obtained starting at the intersection between a and β, and following first a and then β. β-1 is β with reversed direction.
A non-SU(2) gauge invariant quantity that plays a role in certain aspects of the theory, such as in the regularization of certain operators, is obtained by integrating the E field over a two-dimensional surface S

E[S, f] = [integral over S] dSa [E tilda]ia f
Where f is a function on the surface of S, taking values in the Lie algebra of SU(2). Instead of loop observables, you could also take the holonomies and E[S, f] as elementary variables, which is more natural in the C*-algebraic approach.
There are probably ten times as many string theorists as loop quantum gravity theorists. Therefore, string theory is very much the majority view among physicists trying to quantize gravity. It’s very common for you to have two competing theories, and one becomes the majority view, and the other becomes an alternative view. Then the majority view becomes our view of the Universe, and the alternative view fades into memory. Sometimes, it’s because the majority view really is better at explaining what we observe or what we’ve been trying to explain. Sometimes, it’s not really better. Let’s say you have two theories. If someone just happens to think up a solution to one of the problems in one theory, people’s ears will perk up, and they’ll pay more attention to that theory. If there is a belief that one theory is more successful, that will cause more people to pursue that theory. More physics grad students will go into an exciting field that has had recent successes. It will attract more funding. Physicists hope that if it has had recent successes, that implies it will have more successes in the future. However, that becomes a self-fulfilling prophesy because obviously if more physicists are working on one theory instead of another theory, that will cause more progress in the theory with more physicists working on it. The more people trying to figure out how to solve the problems with a theory, the more likely someone will figure something out. You set up a positive feedback loop. The more people working on it, the more progress there will be, which will cause more people to work on it, etc. I don’t mean to say that’s the only thing that causes one theory to be chosen over another. Sometimes, one theory really is better than another. You just have to keep in mind that to some extent, it is a popularity contest. I think it’s good to have more than one theory since it reminds you that none of our theories are the real truth.
You can point to many examples where there is a main theory, that represents the majority view among physicists, and that becomes our view of the Universe, which has or had at least one serious rival, which was less popular, but was a serious alternative theory. The hadrons and the strong force were explained by QCD, although Regge theory was an alternative theory. The hierarchy problem was explained by supersymmetry, although technicolor was an alternative theory, and today the brane world scenario provides an alternative explanation. Quantum gravity is mainly explained by superstring theory, although loop quantum gravity is a serious alternative theory. The rotations of galaxies is explained by dark matter, although MOND was an alternative theory. Most cosmological data, such as the cosmic microwave background, is explained by inflationary cosmology, although the cyclical model is an alternative to inflation.
It’s more complicated than just one theory beating out another, since physicists draw inspiration from anything they can, even theories that have been ruled out. Remember that string theory had its origin in Regge theory which we now consider a totally defunct historical theory. Doubtlessly, loop quantum gravity will have some influence on our view of the Universe. However, I think we can safely say that our view of the Universe in the future will be mainly derived from superstring theory and M-theory.
Lastly, there is one curious thing which may or may not be important. Even though superstring theory and loop quantum gravity approach the problem of quantizing gravity from totally different directions, and involve radically different mathematics, they both require the existence of some sort of circular structure. For superstring theory, it is the closed strings. For loop quantum gravity, it is loops. This possibly might be telling us something about the real Universe.