1. Singularity, t = 0, T = ∞, 13.7 ± 0.2 billion years ago
Initial singularity, origin of spacetime itself, the Big Bang
2. Planck Scale, t = 10-42 seconds or the Planck time, T = 1019 GeV, T = 1032 K
Gravity is as strong as the other forces. All four forces are unified, and you have one force. Then gravity separates from the other forces but still has to be described by quantum gravity. You have quantum gravity effects at the Planck scale. In string theory and M-theory, all the dimensions begin as compactified. According to M-theory, the universe has 10 spatial dimensions which are all the same, and all small. Then due to the Brandenbeurger-Vafa mechanism, three of the spatial dimensions expand into the obvious ones we have today, leaving seven compactified. According to string theory, the details of the topology that the extra dimensions are compactified on, determines the vibration modes of the strings which determine what fundamental particles exist. Also, primordial black holes might be produced at this time.
3. Grand Unification Scale, T = 1016 GeV
Before now, there was no difference between the electroweak and the strong force. They were just one force. Since X and Y bosons are essentially massless compared to the energy scale, they are freely created, and thus quarks and leptons can be freely converted into each other. At the grand unification scale, the grand unified theory undergoes symmetry breaking. It probably undergoes several successive stages of symmetry breaking, as larger groups go through a cascade down to smaller groups. For instance, according to string theory, it could possibly go from E8 x E8 to E6 x E8 to SO(10) to SU(5) to the Standard Model U(1) x SU(2) x SU(3). Also, topological defects such as monopoles would be produced.
4. Inflation, t = 10-36 seconds
At some point, inflation ends. It is probably after grand unification, so that topological defects formed by grand unified theory symmetry breaking, would be rare within our observable universe. The inflaton field rolls down to the bottom of its potential from false vacuum to true vacuum, and after that, inflation occurs at a much more leisurely pace.
5. Supersymmetry Breaking, T = 1 TeV = 1000 GeV, T = 1019 K
Before supersymmetry breaking, supersymmetry was an unbroken symmetry. Supersymmetric particles, such as squarks, sleptons, and bosinos, were as common as what we call normal particles, such as quarks, leptons, and bosons. After supersymmetry breaking, we are left with only normal particles, with the possible exception of the lightest supersymmetric particle.
6. Electroweak Phase Transition, t = 10-11 seconds or 10 picoseconds, T = 100 – 200 GeV, T = 1 – 2 x 1015 K or 1 – 2 quadrillion K
Before this, there was no difference between the electromagnetic and weak force. They were just one force. When the temperature got low enough, there was symmetry breaking. You have the Higgs mechanism go into effect. Before that, you had a complex Higgs doublet, and the three massless intermediate vector bosons. Afterwards, you have the massive W+, W-, and Z0, the massless photon, and a leftover Higgs. This is for the Standard Model Higgs particles. You also have a similar thing happen earlier with the Higgs fields associated with grand unification and supersymmetry.
7. QCD Phase Transition, t = 5 x 10-5 seconds or 50 microseconds, T = 150 – 180 MeV, T = 1.7 x 1012 - 2.1 x 1012 K or 1.7 – 2.1 trillion K
Before this, you had a sea of free quarks and gluons. After this, quarks are moving slow enough that they are confined to hadrons. Therefore, hadrons first come into existence. The strong force is weak at high energies, which is the same at short distances, and strong at low energies, which is the same as large distances. Therefore, normally quarks can never get out of hadrons. However, at high enough energies, the distinction between inside a hadron and outside a hadron disappears, and you have a quark-gluon plasma. Most people think the QCD phase transition is a first order transition, meaning heat is emitted as the transition happens, just as when water vapor condenses to form drops of liquid water. Therefore, the quark-gluon plasma would probably supercool until small bubbles of hadron phase formed. As these bubbles grew, latent heat would be emitted. This would reheat the quark-gluon plasma, limiting the speed at which the bubbles expanded. Heat would be dispersed by neutrino and acoustic waves. Some people call the creation of the first hadrons baryogenesis.
8. Annihilation of Pions, t = 10-4 seconds or 100 microseconds, T = 100 MeV, T = 1012 K or 1 trillion K
If you provide energy equivalent to a particular particle’s rest mass, you can create that particle. If the temperature is enormously high, then just the kinetic energy of the motions of the particles will be enough to create new particles. If the temperature is above a trillion Kelvin, then the kinetic energy will be enough to create pions which have a mass of about 100 MeV. Therefore, since the QCD phase transition, the universe was filled with pions, which were constantly being created to replenish those that annihilated. When the temperature dropped below a trillion Kelvin, pions were no longer being continuously created, and those that remained annihilated each other.
9. Decoupling of Neutrinos, t = 1 second, T = 1 MeV, T = 1010 K or 10 billion K
Neutrinos can easily zip through light-years of lead but the very early universe was so compressed and so dense that they couldn't get very far, and interacted vigorously with other forms of matter. However, about one second after the Big Bang, the density of the universe decreased to about 400,000 times that of water, and neutrinos decoupled from other matter. Since these neutrinos were not reheated by nucleosynthesis, they should now be cooler than the cosmic microwave background radiation. They should be 2 Kelvin instead of 2.725 Kelvin. These primordial neutrinos should now fill the universe, but we can't detect them because they move so slowly.
10. Annihilation of Electron-Positron Pairs, t = 10 seconds, T = 500 keV, T = 5 x 109 K or 5 billion K
The rest mass of an electron is about 511 MeV, so it takes twice that much energy to create an electron-positron pair. If you multiply 511 MeV by Boltzmann’s constant, k = 1.38066 x 10-23 J/K, you get about 5 billion Kelvin. That means that at this temperature, two particles colliding head on will often have enough kinetic energy to create an electron-positron pair. Therefore above this temperature a large number of electrons and positrons will be continuously created by just the collisions between particles. When the temperature drops below this, electrons and positrons will stop being created in such numbers, and most of those remaining will annihilate each other. Some people refer to this as leptogenesis.
11. Nucleosynthesis, t = 180 seconds, T = 100 keV, T = 109 K or 1 billion K
At about this time, the temperature dropped to the point where a proton and neutron could stick together forming a deuterium nucleus. Then deuterium nuclei could bind together to create helium nuclei. This is called nucleosynthesis. This is responsible for the fact that before the first stars, the baryonic matter was 75% hydrogen and 25% helium.
12. Decay of Lone Neutrons, t = 1000 seconds, T = 50 keV, T = 5 x 108 K or 500 million K
A lone neutron has a lifetime of 918 seconds, after which it will decay into a proton, electron, and antineutrino. Any neutrinos that are not bound in nuclei decay at this time.
13. End of Radiation-Dominated Era, t = 10,000 years, T = 1 eV, T = 12,000 K, z = 3454
Up until this point, the Universe was radiation-dominated. Here it makes the transition from radiation-dominated to matter-dominated. It remained matter-dominated until the present epoch when we have comparable contributions from the matter density and vacuum density. In the future, it will be vacuum-dominated. The end of the radiation-dominated era is when gravity began to amplify small fluctuations in the density of matter. This led to matter collapsing under gravity on various size scales to lead to stars, galaxies, and clusters of galaxies.
14. Recombination, t = 380,000 years, T = 3000 K, z = 1088
Before this, you had atomic nuclei and free electrons. After this, atomic nuclei and electrons are moving slow enough that they can bind to form atoms. Therefore, atoms first come into existence. In chemistry, when an atomic nucleus combines with electrons to form an atom, they call it "recombination". However, in this case, they are combining for the first time. A better name would be "combination" instead of recombination, which is the official name. Before this, the Universe was filled with electrically charged plasma. After this, it was filled with neutral hydrogen. Plasma absorbs light at all frequencies, while electrically neutral gases tend to be transparent except for certain frequency bands. Therefore, recombination was the first time that photons could travel for long distances without being absorbed. The first photons that were set free to travel are now being detected by us as the cosmic microwave background radiation.
15. Reionization, t = 200,000,000 years or 200 million years, T = 50 K, z = 17 ± 5
This is when the neutral hydrogen, which had cooled after the Big Bang, became hot and ionized again. This was probably caused by the first stars, so this would mean the first stars were formed about 200 million years after the Big Bang. Also during this time, you have the formation of large scale structure due to the clumping of matter under gravity. We believe that galaxy formation is caused by gravitational clumping that was seeded by dark matter. We can detect a rough correlation between anisotropies in the CMB and large scale structure.
16. Present Era, t = 13.7 x 109 years or 13.7 billion years, T = 2.725 K, z = 0
This is the present. The Universe is 13.7 ± 0.2 years old. The cosmic microwave background now has a temperature of 2.725 K. During the present era, Ωm = 0.3 and ΩΛ = 0.7. Therefore, during the present era, the matter density is becoming of the same order as the vacuum density. The fact that this happens to be happening during the time we are is called the cosmic coincidence problem.
Let's say you are watching ice freeze on a pond in the middle of winter. The ice does not form on the surface everywhere at once, and it doesn't grow from one single point. Instead, the water begins to freeze in many places independently, and the growing plates of ice join up in a random fashion leaving zig-zag boundaries between them. These boundaries are called topological defects, and the same thing happens in the early universe. You might initially think that ice crystals have more symmetry then liquid water, but actually the liquid water has more symmetry. In liquid water, the water molecules jostle each other randomly. Therefore, it looks the same in every direction. The liquid water is isotropic. From the point of view of a hypothetical observer in the middle of a drop of water, looking at the water molecules, they would see basically the same thing in every direction, so liquid water is isotropic. However, when liquid water freezes into ice, it forms a hexagonal lattice. The water molecules are no longer in a random orientation, so you don't see the same thing in every direction, so it's no longer isotropic. When water freezes, it breaks the rotational symmetry, so you have symmetry breaking. When water goes from liquid to solid, that's called a phase transition. When you have liquid water, the water molecules are pointing randomly, and when it freezes, they are no longer pointing randomly. Which direction they end up pointing is randomly determined, but after it's chosen, they are locked in, and all the surrounding molecules have to line up in a prescribed way. If you have a large amount of water, all at freezing temperature, this will be happening at many different locations, which are too far from each other to know what the others are doing. Therefore, the crystalline structure of the ice will be oriented along different directions in each of these different domains, and when they come into contact, you have an obvious boundary between them. It's the symmetry breaking that gives rise to the different domains with boundaries between them. The boundaries are called topological defects. You have this whenever you have symmetry breaking.
For instance, you have the same thing with a ferromagnet when its temperature falls below its Curie temperature, so the molecules are no longer pointing in random directions, but instead line up, and they line up in different directions in different domains. Therefore, phase transitions with symmetry breaking give rise to topological defects. As I just listed in the history of the Universe, phase transitions and symmetry breaking were common in the early universe. Particle physics uses symmetry breaking to unify the particles and forces. Particle physics assumes large gauge groups containing smaller gauge groups. Therefore, you have a succession of symmetry breaking which should give rise to topological defects. In the examples of freezing water, ferromagnetism, grand unified theory symmetry breaking, and electroweak symmetry breaking, a decrease in temperature causes a decrease in symmetry, which causes something that was previously random to choose a preferred direction, and which direction is not the same in disconnected regions, giving rise to different domains with boundaries between them, called topological defects.
In the standard hot Big Bang, the spontaneous breaking of fundamental symmetries is realized as a phase transition in the early universe. There are several symmetries which break successively in the early universe. In each of these transitions, spacetime gets oriented by the presence of the Higgs field. The field orientation signals the transition from a state from a state of higher symmetry to a state of lower symmetry, so in the final state, the system obeys a smaller group of symmetry rules. It is the orientation of the Higgs field that breaks the higher symmetry between particles and forces to a lower symmetry. The particle physics symmetry breaking we understand the best is electroweak symmetry breaking since it takes place at energies low enough for us to reach in our particle accelerators. You also have grand unified theory symmetry breaking. These involve the Higgs mechanism. The Higgs field pervades all of space. As the universe cools, the Higgs field can take different ground states, called the vacuum states, of the theory. In a symmetric ground state, the Higgs field is zero everywhere. The symmetry breaks when the Higgs field takes a nonzero finite value. Because this happens at the same time in distant parts of the universe that are not in casual constant, the Higgs field would take different values in different parts of the universe.
In the expanding Universe, widely separated regions in space have not had enough time to communicate amongst themselves and are therefore not correlated, due to lack of casual contact. Therefore, different regions ended up with different arbitrary orientations of the Higgs field, and when they merged together, it was hard for domains with different preferred directions to adjust themselves and fit smoothly. In the interfaces of these domains, you have topological defects. This is similar to freezing ice, where the molecules in different regions are aligned in different directions before they are in contact, and then when they make contact, there is a boundary between them. This mechanism was described by Kibble in 1976, and is called the Kibble mechanism. Not every phase transition involves symmetry breaking. When steam condenses into liquid water, the molecules are in a random configuration both before and afterwards. The symmetry does not decrease. Similarly, during the QCD phase transition, the symmetry does not decrease. It proceeds by bubble nucleation. Bubbles of the new phase form and become larger and larger until they merge, but since the symmetry is the same as before, there is no boundary between them. In the condensation of water, the droplets of water merge, and there is no boundary between them. In the QCD phase transition, when the regions of hadronic matter merge, there is no boundary between them. Therefore, it does not give rise to topological defects.
Separate from whether the symmetry does or does not decrease, another way of classifying phase transitions is whether they are first order or second order. The old fashioned definition, according to Ehrenfest classification scheme, is that first order transitions have a discontinuity in the first derivative of the free energy. Second order phase transitions have a discontinuity in a second derivative of the free energy. According to the modern definition, first order phase transitions involve a latent heat, and the system absorbs or releases a fixed amount of energy. Second order phase transitions have no associated latent heat.
Here I list some types of topological defects.
1. Domain Walls - These are two-dimensional surfaces that form when a discrete symmetry is broken at a phase transition. A network of domain walls effectively partitions the universe into cells. The gravitational field of a domain wall is repulsive rather than attractive. Domain walls are associated with models in which there is more than one separated minimum.
2. Cosmic Strings - These are one-dimensional objects that form when an axial or cylindrical symmetry is broken. Strings can form due to grand unified theory symmetry breaking or electroweak symmetry. Ten kilometers of a typical GUT string would have the same mass as the Earth. Cosmic strings are a candidate for dark matter. A cosmic string forming a closed loop is called a vorton. Cosmic strings are associated with models in which the set of minima are not simply connected, meaning the vacuum manifold has holes in it.
3. Monopoles - These are zero-dimensional objects that form when a spherical symmetry is broken. Monopoles are massive and carry magnetic charge. Monopoles are predicted by grand unified theories. The monopole problem is one of the problems solved by inflation.
4. Textures - These form when larger, more complicated symmetry groups are completely broken. Textures are delocalized topological defects which are unstable to collapse.
5. Skyrmions - This is a quasiparticle corresponding to topological twists or kinks in a spin space. A skyrmion is a soliton with spin and statistics different from those of the underlying fields in a nonlinear field theory.
Another unanswered question is why do we have an overwhelming preponderance of matter over antimatter, when particle physics, such as Dirac’s equation, treats matter and antimatter exactly the same. This is called the baryon asymmetry of the Universe. Andrei Sakharov laid out the three Sakharov criteria that must be met to explain the baryon asymmetry. You need C violation. CP violation, and thermal equilibrium. Our best guess for explaining it comes from grand unified theories, and other possible explanations involve supersymmetry or the electroweak phase transition. I explain this in more detail in my paper Beyond The Standard Model.
In the traditional Big Bang model, and thus the traditional inflationary model with a fundamental Big Bang, there was an initial singularity. For some people, this is no problem. You would expect that the origin of the entire Universe to be something undefined like a singularity. Some people say that the singularity means our theories break down, but you would expect them to break down at the origin of the Universe. Other people just don't like the idea of an initial singularity, and they want to get rid of it. The main way to get rid of it is to invoke eternal inflation, and say time extends infinitely backwards. However, other people want to say the universe existed for a finite length of time, but still get rid of the initial singularity. This is basically the goal of quantum cosmology, which is applying quantum mechanics to the origin of the universe. The first example of quantum cosmology remains the most famous example, which is the Wheeler-De Witt equation, which is supposed to describe the wavefunction of the entire universe. Usually, you can use quantum mechanics to describe subatomic systems, except here you're using it to try to describe the entire universe. At any instant, the universe is described by the geometry of three spatial dimensions, as well as matter fields that are present. Given this data, you can, in principle, use the path integral to calculate the probability of evolving to any other prescribed state at a later time. However, this still requires a knowledge of the initial state. It does not explain the initial state.
Quantum cosmology is a possible solution to this problem. In 1983, Stephen Hawking and James Hartle came up with a theory of quantum cosmology called the No Boundary Proposal. The path integral involves a sum over four dimensional geometries that have boundaries matching the initial and final three geometries. The Hartle-Hawking proposal is simply forget about the initial three geometry, and instead only include four geometries that match the final three geometry. The path integral is interpreted as giving the probability of a universe with certain properties being created from nothing. In practice, calculating probabilities in quantum cosmology using the full path integral is extremely difficult, so you have to use an approximation. This is called the semiclassical approximation because its validity lies between that of classical and quantum physics. In the semiclassical approximation, you argue that most of the four dimensional geometries occurring in the path integral will give very small contributions to the path integral, and so these can be neglected. The path integral can be calculated by just considering a few geometries that give a particularly large contribution. These are called instantons. Instantons don’t exist for all possible choices of boundary three geometries. However, those three geometries that do admit instantons are more probable than those that don’t. Therefore, you restrict your attention to geometries close to those. The path integral is a sum over geometries with four spatial dimensions. Therefore, an instanton has four spatial dimensions and a boundary that matches the three geometry whose probability you want to compute.
The Coleman-De Luccia instanton was discovered by Coleman and De Luccia in 1987. It assumes that the universe was initially in a state of false vacuum. A false vacuum is a classically stable excited state that is quantum mechanically unstable. In quantum theory, the false vacuum may tunnel to its true vacuum. Coleman and De Luccia showed that false vacuum decay proceeds via the nucleation of bubbles in the false vacuum. Inside each bubble, the matter has tunneled. It turns out that the interior of such a bubble is an infinite open universe in which inflation may occur. The cosmological instanton describing the creation of an open universe via this bubble nucleation is called a Coleman-De Luccia instanton.
Lastly, I want to discuss the anthropic principle in more detail. It might seem in contradiction with the Copernican principle, which says that we are typical observers. The anthropic principle says that we aren’t completely typical because we are in a time and place that life would arise. Otherwise we wouldn’t be here. For instance, if you chose a point in the Universe at total random, it would be very unlikely to be as close to a star as we are. However, it is not unlikely or surprising that we are close to a star because life would have to arise close to a star. In other ways, you can explain why we are at the time and place we are on the grounds that life would be more likely to arise at our time and place. For instance, if the Universe will exist for infinite length of time into the future, then isn’t it surprising that we are only 13.7 billion years after the Big Bang instead of a googol, 10100 years, or a googolplex years? Not really, because there is a window of time in the history of the Universe in which life is possible. Life requires heavy elements that are made in stars. Therefore, life could only arise after the first generation of stars have gone supernova, and distributed the heavy elements into the interstellar medium. If supernova are rare events in the Universe, you might think it would be surprising if one occurred near us shortly before the formation of the Solar System, but actually, that would not be surprising since it would make it more likely that we would be here. Similarly, in the deep future, all the stars will burn out, leaving white dwarves, neutron stars, and black holes. There won’t be enough material to form new stars. According to thermodynamics, all matter will eventually end up in giant black holes, which will eventually evaporate. Eventually, the last protons will decay, and baryonic matter will no longer exist. Life will be impossible in such a universe. Life is only possible during a window in cosmological history, when you have second generation stars like the Sun. It is therefore hardly surprising that we are located at the time we are in the history of the Universe.
You can use the anthropic principle to explain the cosmic coincidence problem, which is why are we located at the time when the matter density and vacuum density are of the same order of magnitude when usually they are not. Life would arise after matter-domination so that matter can self-gravitate into stars. The matter density has to be dense enough that stars are likely to form. Like I said, it has to be after the first generation of stars so there will be heavy elements necessary for life. At the same time, life is unlikely to arise in a universe dominated by vacuum energy. If the vacuum energy density is too much larger than the matter density, the gravitational attraction can’t overcome the enormous repulsive effect of the vacuum, and it’s unlikely matter can collapse gravitationally to form stars. Therefore, life will be most likely to arise when the matter density is comparable to the vacuum energy density, which is when we are now. The anthropic principle is actually important in our current view of the Universe, which is M-theory. The most advanced physics is M-theory, and we have recently expanded M-theory to allow for de Sitter space, so you can then combine M-theory with inflationary cosmology. There are an infinite number of points in the moduli space of M-theory, not just the five superstring theories, which do not correspond to the real Universe. The real Universe corresponds to an unknown point in the non-perturbative regime of M-theory that is consistent with a de-Sitter-like universe.
Now imagine that you have inflationary cosmology. You have chaotic inflation. Some parts of the universe undergo rapid inflation, like shortly after our Big Bang, and other parts have a more leisurely expansion, like we’re experiencing now. These different parts are not casually connected. Now these different parts of the universe end up with different types of vacuum, which correspond to different points in the moduli space of M-theory. Therefore, all possible points in the moduli space of M-theory are realized somewhere in the universe. You could call these disconnected parts of the universe, different universes. Most of these will give rise to universes where life is not possible. We are in one of the few universes within which life is possible. That explains why we are in the universe that we are in, even if it might seem unlikely. Even if it seems that there are unlikely things that are necessary for life to be possible, obviously we are going to be in a universe that has those apparently unlikely things, as opposed to a universe that doesn’t. Therefore, if you combine M-theory, inflationary cosmology, and the anthropic principle, you get our view of the Universe. The anthropic principle is probably true and necessary. Despite that, many cosmologists shy away from the anthropic principle, or at least stating it explicitly, because many people misuse it, or try to use it to explain anything we can’t explain. The anthropic principle can’t be used to explain everything.
When we observed the redshift of the galaxies, you could have explained that by saying we were located at the center of the Universe. We did not say that because that would violate the Copernican principle. The anthropic principle does not offer any way around the Copernican principle in this case because there is no reason why life would be more likely to arise at the center of the Universe. Some people have also used the phrase "anthropic principle" to mean that the presence of life on Earth is itself a piece of experimental data that you can take into account when building your theories. Just as you observe data from telescopes and particle accelerators, you can observe that life exists on Earth. In the 19th Century, Lord Kelvin advocated that the Earth was 107 years old, based on its cooling time. Evolutionary biologists were able to argue that this was not enough time for all species to evolve. They were using the observation of life on Earth to disprove an estimate for the age of the Earth. Their claim was vindicated by the discovery of radioactivity which allowed both the dating of the Earth, and showed the flaw in Kelvin's argument. This was an important astronomical argument being drawn from the observation of life on Earth.
The synthesis of the higher elements is rather difficult due to the nonexistence of stable elements with atomic weights A = 5 or A = 8. This makes it hard to build up nuclei by collisions of 1H, 2D, 3He, and 4He nuclei. The only reason that heavier elements are produced at all is because of the reaction
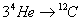
34He -> 12C
A three body process like this will only proceed at a reasonable rate if the cross section for the process is resonant, if there is an excited energy level of the carbon nucleus that matches the typical energy of three alpha particles in a stellar interior. The lack of such a level would lead to a negligible production of heavy elements, and no carbon-based life. Recognizing this, Hoyle predicted that carbon would display such a resonance, which was later found. Now, in some ways this is like Lord Kelvin and the age of the Earth, where the observation of life on Earth leads to a conclusion, in this case, that there must exist such a resonance. Still, there is a feeling that we are lucky that there is such a resonance since otherwise we wouldn’t be here. Maybe we are lucky. Maybe there is a large number of universes, called an ensemble, or a large number of parts of the universe, and we are in one of the few that have such a resonance. If that’s true, it would hardly be surprising that we would be located in one of the few universes or parts of the universe that have such a resonance.
Here’s another example. We have three generations of fermions. Each has two quarks, one with a charge of 2/3, and one with a charge of -1/3. With the second and third generations, the quark with a charge of 2/3 is heavier than the quark with a charge of -1/3. In the first generation, the quark with a charge of -1/3, the down quark, is heavier than the quark with a charge of 2/3, the up quark. For that reason, a lone proton is stable, and a lone neutron is unstable. Let’s say instead, in the first generation, the 2/3 quark was heavier than the -1/3 quark, like in the other two generations. Then a lone neutron would be stable, and a lone proton would be unstable. Then in the early universe, all the lone protons would decay, and the lone neutrons would not. You could still have some atoms form with nuclei that contain protons and neutrons in a bound state. However, if free protons decay in a few minutes, there will be very little hydrogen in the Universe. There would no stars, and no life in the universe. Life would be impossible. Now what does this tell us? The masses of the fermions are derived from interaction with the Higgs field, although we can’t calculate the values of the masses. You could imagine that in different parts of the universe, the Higgs field is different, which causes the values of the masses of the fermions to be different. Maybe in most parts of the universe that have three generations of quarks and leptons similar to ours, the up quark is heavier than the down quark, and thus have no life. It would not be surprising that we are in a part of the universe, or a universe, in which life is possible, even if life is not possible on most parts of the universe, or most universes.
Paul Dirac noticed the existence of large dimensionless numbers in physics, which is called Dirac’s large number hypothesis. Today, we can explain it with anthropic arguments, such as pointing out that life could not have arisen until heavy elements were produced in first generation stars. Lastly, I just want to say that there are tons of crackpots who know nothing about physics, but invoke the name "anthropic principle", but they are referring not to the real anthropic principle, but instead to a garbled misunderstanding of it which I won’t dignify by repeating here. This might be part of the reason why some in the physics community shy away from it. However, the anthropic principle is probably true as far as it goes. It’s probably necessary to explain some aspects of what we observe of the Universe.