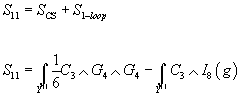
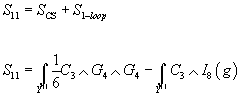
S11 = SCS + S1-loop
S11 = ∫Y11 (1/6) C3 ∧ G4 ∧ G4 - ∫Y11 C3 ∧ I8(g)
where
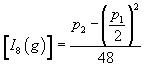
[I8(g)] = (p2 - (p1/2)2)/48
written in terms of the Pontryagin classes of the tangent bundle.
Using cobordism, Witten uncovered a structure related to E8 index theory by writing the above action on a twelve-manifold Z12 whose boundary is the M-theory eleven-manifold Y11. In twelve dimensions, the topological part of the action is then

S12 = ∫Z I12
S12 = ∫Z (1/6) G4 ∧ G4 ∧ G4 - G4 ∧ I8
You have the mod 6 congruence which was derived by S. P. de Alwis using physical arguments related to Horova-Witten boundaries, and by Edward Witten using E8 index theory.
You can write the Chern-Simons term in an exponentiated form as
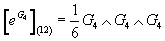
[eG4](12) = (1/6)G4 ∧ G4 ∧ G4
which looks like a character. Obviously, this encodes the correct normalization factor.
Next look at the one-loop term. The total string class is defined in terms of the individual string classes by
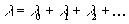
λ = λ0 + λ1 + λ2 +…
where λ0 = 1, λ1 = p1/2 is the usual string class, λ2 = p2/2 is the second string class, and so on. The exponentiated class or total string character is defined by
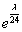
eλ/24
whose degree eight component gives
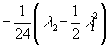
-(1/24)(λ2 - ½ λ12)
which is exactly the one-loop gravitational polynomial I8, as it shows up in the action with the minus sign. This is analogous to writing the second Chern character in terms of the Chern classes as
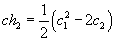
ch2 = ½ (c12 - 2c2)
Then the total topological action can be written as
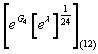
[eG4[eλ]1/24](12)
the degree twelve component.
This apparently predicts a term
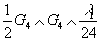
½ G4 ∧ G4 ∧ λ1/24
that can be written in terms of
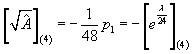
[squareroot of A hat](4) = -(1/48) p1 = -[eλ/24](4)
In fact, you can ask in a different but related context if you can replace the K-theoretic formula
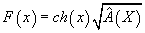
F(x) = ch(x)[squareroot of A hat(X)]
for the RR fields with something like
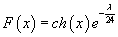
F(x) = ch(x)e-λ/24
They match for the two lower degrees of the gravitational part, which is 0 and 4, but not the degree 8.
Anyway, you can find a rationale to exclude such terms, as well as terms containing λ3, on the basis of parity. You want to retain terms like
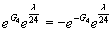
eG4 eλ/24 = -e-G4 eλ/24
which kills the terms with an even number of G4’s and keeps the ones with an odd number of G4’s. Therefore, the total topological action is given by the parity-odd part of the twelve-form component of the character. The Lagrangian of the 11-dimensional supergravity has a sign of the 3-form potential C3. along with a reversal in sign of an odd number of space coordinates.
The phase of the M-theory partition function would then be written as
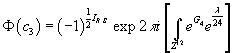
Φ(C3) = (-1) ½ IR.S. exp 2πi[∫Z12 eG4 eλ/24]
where you pick the degree twelve component out of the integrand. The sign ambiguity in the phase of the Pfaffian of the Rarita-Schwinger operator is given in terms of the Rarita-Schwinger action IR.S..
Now, we make an analogy with the construction of the Chern character based on ordinary curvatures of connection one-forms. This suggests that an analogous theory based on the Pontryagin classes or the string classes. Here is the Chern character.
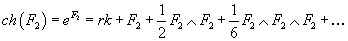
ch(F2) = eF2 = rk + F2 + ½ F2 ∧ F2 + (1/6) F2 ∧ F2 ∧ F2 + …
Now, do the same thing with G4.
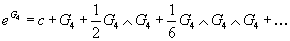
eG4 = c + G4 + ½ G4 ∧ G4 + (1/6) G4 ∧ G4 ∧ G4 + …
The Chern character should be written in terms of the Lie-algebra valued curvature, whose trace we’ve suppressed. The character corresponding to G4 does not have a value since G4 does not correspond to a structure group in a literal sense. If it is a 2-gerbe, then the simplest way is to take it to be abelian, and thus corresponding to a U(1). If you write the C-field in terms of the E8 gauge fields, such as C3 = CS3(A), then G4 might have some nonabelian aspect to it.
Now look at this equation.
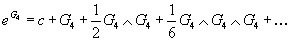
EG4 = c + G4 + ½G4 ∧ G4 + (1/6)G4 ∧ G4 ∧ G4 + …
You can think of this as defining a sort of M-theoretic character analogous to the Chern character. Here “c” refers to the appropriate concept in this case that replaces the rank of the bundle for the case of K-theory. The E8 and Rarita-Schwinger indices are then encoded in
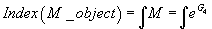
Index(M object) = ∫M = ∫eG4
where the M objects are
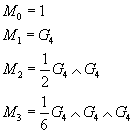
M0 = 1
M1 = G4
M2 = ½G4 ∧ G4
M3 = (1/6)G4 ∧ G4 ∧ G4
where M1 corresponds to the M2-brane, M2 corresponds to the M5-brane, or little M-theory, and M3 corresponds to M-theory. Therefore the M-branes and M-theories are unified.
In order to be technically correct, M must also include a gravitational correction term eλ/24. You simply replace M with
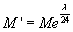
M’ = Meλ/24
You exclude odd parity for odd-rank characters, and even parity for even-rank characters.
The Chern-Simons construction for Type IIA string theory and for M5-branes is similar. In both cases, you have a manifold of dimension 4k + 2 with k = 1 for the 5-brane, and k = 2 for the Type IIA string theory. The Chern-Simons construction requires extending the (4k + 2)-dimensional X to a (4k + 3)-dimensional manifold X x S1, which in the case of Type IIA is just the extension to M-theory. Then the construction requires extending the resulting manifold to a (4k + 4)-dimensional coboundary N such that ∂N = X x S1. In the case of IIA and M-theory, this is the manifold Z. In both cases, you are extending the manifold together with a four-class, so this requires the vanishing of the spin cobordism cohomology group.
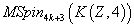
MSpin4k + 3(K(Z, 4))
R. E. Stong showed that this was the case for k = 2, and M. J. Hopkins and I. M. Singer showed that this was the case for k = 1. Similar to the Chern-Simons term in M-theory, you can write the corresponding quadratic term involving only G4 on N8 in an exponential way.
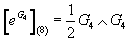
[eG4](8) = ½g4 ∧ G4
which is the formula derived by Witten, and also in a more general situation by Hopkins and Singer. This suggests there is a generalized cohomology theory in which G4 lives, and the character is a multiplicative map from the theory of M-objects to 4kth cohomology.
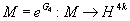
M = eG4 : [curly M] → H4k
where [curly M] is the generalized cohomology theory that describes M-theory. Remember that the Chern character is a map from K-theory to even cohomology
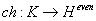
ch : K → Heven
and satisfies for two vector bundles E and F

ch(E ⊕ F) = ch(E) ⊕ ch(F)
ch(E ⊗ F) = ch(E) ∧ ch(F)
We want the M-theory character to have properties analogous to the Chern character so we want it to satisfy
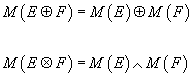
M(E ⊕ F) = M(E) ⊕ M(F)
M(E ⊗ F) = M(E) ∧ M(F)
where E and F are M-objects. Notice that dM = 0 since G4 is closed due to the Bianchi identity.
For K-theory, the objects corresponding to the two-form curvature F2 are vector bundles. Therefore, the corresponding M-objects related to G4 would be 2-gerbes, 2-vector bundles, etc.
A connection on a U(1)-bundle looks locally like a 1-form, so you can integrate it along a path and compute how the phase of charged particles changes when you move it along that path.
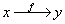
x → y
f : x → y is a path f from point x to point y.
If you categorify this whole idea once, you get a connection that looks locally like a 2-form, called a connection on a U(1)-gerbe. This is just a gadget that you can integrate over a surface to compute how the phase of a charged string moves when you slide it along that surface.
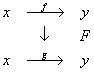
F : f → g is a path F from the path f to the path g.
If you categorify once more, you get connection on a U(1) 2-gerbe. This is something that looks locally like a 3-form, which describes what happens when you move 2-branes around. Since 11d supergravity has a 3-form, and M-theory has 2-branes, you therefore need to categorify the concept of a U(1) bundle twice, and use 2-gerbes when discussing M-theory.
From the general structure of the M-theory character, and from the mod 24 congruence of the string class, the theory should be some form of elliptic cohomology related to topological modular forms. There should also be some relation to E8 and Rarita-Schwinger bundles.
One way to better understand gerbes is to think of them as differential objects. You now replace local holomorphic functions hαβγ on a complex manifold by smooth functions, and assume that the values lie in the group U(1) of unit complex numbers. There is then the idea of a unitary connection on a grebe, provided by real differential 1-forms Aαβ and 2-forms Fα such that

iAαβ + iaβγ + iAγα = h-1αβγdhαβγ
Fβ - Fα = dAαβ
Then
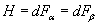
H = dFα = dFβ
is the global closed 3-form, which is defined to be the curvature of the connection. The de Rham class
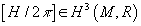
[H/2π] ∈ H3(M, R)
is integral, just as [F/2π] is the first Chern class if F is the curvature form for a connection on a line bundle. Equivalence classes of grebes with connections like these are familiar in the theory of Cheeger-Simons differential characters of degree 2.
The best known example of a grebe with connection arises when the manifold M is a compact simple Lie group G. There is a natural gerbe on G whose curvature is a multiple of the bi-invariant 3-form B(X, ([Y, Z]) where B is the killing form. For G = U(n), this is tr(g-1dg)3. Whereas a line bundle has holonomy around a closed surface. More generally, if the curvature of a gerbe vanishes, then there is a holonomy in H2(M, U(1)). For example, B(X, [Y, Z]) vanishes on a T ⊂ G because T is abelian, so the gerbe is flat there. It is a rather subtle mod 2 invariant of the group. For a map of a closed surface f : Σ → G, the curvature is zero on the 2-manifold Σ. In this case, the holonomy evaluated on the fundamental cycle of Σ is the R/Z invariant called the Wess-Zumino term.
The integral cohomology class in H3(M, Z), defined by the curvature form of a gerbe with connection, exists for topological reasons. In Cech cohomology, it is represented by δ log hαβγ/2πi. Since the homotopy classes [X, K(Z, 3)] of the Eilenberg-MacLane space K(Z, 3) are just the degree 3 cohomology, what structure does this space have?
One model for K(Z, 3) is the classifying space BPU(H) for the projective unitary group of the Hilbert space. A map X → BPU(H) defines a bundle of projective Hilbert spaces over X, and this provides a gerbe the same as the finite dimensional case. The difference is that the class in H3(X, Z) is (n + 1)-torsion for PGL(n + 1, C) whereas any class can be represented by a projective Hilbert space bundle. This forms the basis of twisted K-theory. to a bundle of projective Hilbert spaces, you can associate a bundle of Fredholm operators Fred(P) since the scalars act trivially by conjugation, and the twisted K-group Kp(M) is defined to be the space of homotopy classes of sections of Fred(P) → M. This group, which is a module over K(M), is important in D-brane charges in superstring theory, although calculations using Mayer-Vietoris sequences are handled by using the line bundle Lαβ defining the gerbe rather than the infinite-dimensional projective bundle. Unitary grebes take their place in a hierarchy, beginning with functions to the circle, then principle circle bundles, then grebes, then 2-gerbes, etc. The canonical line bundle of a complex manifold is the object underlying the first Chern class, and understanding the geometry of the 2-gerbe behind the first Pontryagin class is what you have to do in order to take it to the next level.
For an interesting discussion of more relations between physics, K-theory, and elliptic cohomology, read John Baez’s TWF255.