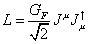
The Fermi constant deduced from neutron beta decay is slightly smaller than the Fermi constant deduced from muon decay. This is because the up, down and strange quarks interacting by the weak force are not flavor eigenstates but are rotated by a mixing angle, θc, called the Cabibbo angle. This was invented by Nicola Cabbibo in 1963, when the up, down, and strange quarks were the only quarks known. Therefore, the flavors of quarks recognized by the strong force interaction are not exactly the same as those recognized by the weak interaction. Actually, they are linear combinations. Here is the Fermi Lagrangian.
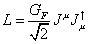
L = (GF/[squareroot of 2]) JuJu†
where
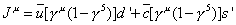
Ju = [u bar][[gamma]u (1-[gamma]5)]d' + [c bar][[gamma]u(1-[gamma]5)]s'
where you have the following rotations
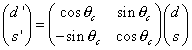
where θc is the Cabbibo angle. θc ~ 13°.
When the up, down, and strange quarks were the only quarks known, there was the problem that the K0 → μ+ μ- had a branching ratio 20 times smaller than predicted. This was solved by Glashow, Illipoulos, and Maini in 1970 by the GIM mechanism, which was just assuming a fourth quark called charm. In 1974, a team at Brookhaven National Laboratory led by Sam Ting discovered a particle they named J, and another team at SLAC at Stanford led by Burt Richter discovered the same particle which they named Ψ. This J/Ψ particle was actually charmonium, which is a charm-anticharm meson, and thus the charm quark was discovered. With more quarks, there are more mixing possibilities. The GIM mechanism was later extended to three families, with six quark flavors. At first it was assumed that there were only two generations of fermions. In 1973, Makato Kobayashi and Toshihide Maskawa considered the possibility of CP-violation in such a model, and determined that CP-symmetry is conserved with two generations of fermions. They then postulated a third generation of fermions, and showed that such a model allowed CP-violation. In the generalized theory, CP-violation is described in terms of a single parameter, the relative phase in the matrix of couplings of the W boson between any up-type quark and any down-type quark. The three generation matrix generalizes the Cabbibo matrix of the two generation theory, and is called the KM matrix, or the CKM matrix, named after Cabbibo, Kobayashi, and Maskawa. Of course, this was before there was any experimental evidence for a third generation of fermions. Then in 1975, the tau lepton became the first third generation fermion detected, and the KM-matrix became accepted. The general form of the current is
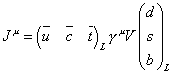
where V is the Kobayashi-Maskawa matrix. It's also written KM-matrix, CKM-matrix, or UKM
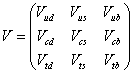
There is freedom in the matrix allowing permutation between various generations. You can fix this freedom by ordering the quarks by their masses. An n x n matrix has n2 real parameters so there is further freedom in the phase structure in the KM-matrix. You can fix this by demanding that the matrix have the minimum number of phases. In the three generations case, the KM-matrix has a single phase which is the source of the weak CP-violation. The KM-matrix can be parametrizated in different ways, the following being the standard way.
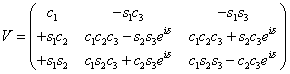
Here are the values derived from experiment.
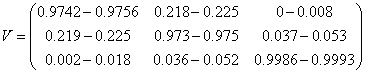
Here is an alternative parametrization proposed by Wolfenstein.
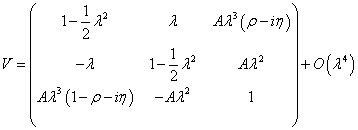
Since neutrinos have mass, there is a similar matrix relating their mass eigenstates to their flavour eigenstates, called the Maki-Nakagawa-Sakata matrix, which causes neutrino oscillation.
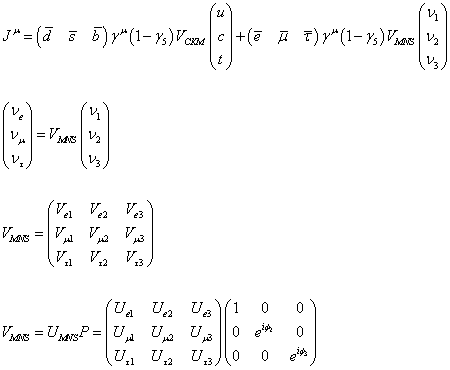
where P is the Majorana-phase matrix.
The term Yukawa coupling is a general term for an interaction term between fermions and scalars of the form
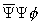
[psi bar][psi][phi]
At short distances, the gluon is the mediator of the strong force between quarks. This is the pure strong force. Gluons are confined to the same space to which quarks are confined. Thus, they never get out of the nucleon to create a force between one nucleon and another nucleon, such as in a nucleus, to bind the nucleus together. Therefore, gluons are useless for a long distance force, where long can be as short as 2 or 3 fermi. 1 fermi = 10-15 meters.
However, mesons can exist outside nucleons and can, thus, be exchanged over larger distances as compared to gluons. Therefore, it is assumed that the strong interactions between nucleons in a nucleus is achieved by exchanging mesons, specifically the pion, as opposed to the strong interaction between quarks which is achieved by exchanging gluons. The creation of these pions goes back to processes between quarks and gluons that take place inside a nucleon. The meson-exchange force is not a fundamental force. It is a residual strong force, in contrast to the pure version of the strong force mentioned above. It is just a spin-off of complicated quark gluon processes. Therefore, meson-exchange forces are typically weaker than the pure gluon exchange between quarks. The idea of meson exchange goes back to the original belief that the pion was the mediator of the strong force. This later seemed ridiculous since π+ itself was supposed to be an up quark and down antiquark but we still use the idea today as a residual force that binds nucleons into a nucleus.
This is analogous to the fact that the pure electromagnetic force acts between protons and electrons inside the atom, confining them to an atom, while a weaker residual electromagnetic force acts between atoms, binding them together to form molecules.
Sometimes, in order to quantize the gauge theory you must add a gauge fixing term and the corresponding Faddeev-Popov term. The first term breaks the gauge symmetry and therefore removes the divergence of the functional integral. The second term improves the integration measure to provide correct predictions for gauge invariant observables. The Faddeev-Popov term includes auxiliary anti-commutative fields called the Faddeev-Popov ghosts. The general form of a gauge-fixing term is
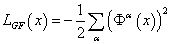
The corresponding Faddeev-Popov term is
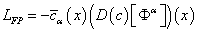
where cα and [c bar]α are auxiliary anti-commutative fields called Faddeev-Popov ghosts. The most famous gauge-fixing term is the Feynman gauge.
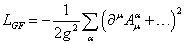
The corresponding Faddeev-Popov term is
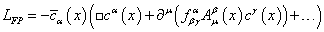
After gauge fixing, you can bring the path integral to a form which contains unphysical ghost fields. The path integral may also be shown to be manifestly independent of gauge fixing. Then the action has a symmetry resulting of the original gauge invariance, which is lost when gauge fixing, called BRST symmetry, named after Becchi, Rouet, Stora, and Tyupin. Physical arguments lead to the conclusion that only states invariant under the BRST symmetry are physical.
The Standard Model can be used to calculate various quantities which can then be tested by experiment. So far, all experimental data is consistent with the Standard Model. A typical high energy physics experiment measures cross sections. Cross sections measure the effective area of interaction between beam and target particles. Cross sections are measured in barns, where 1 barn = 10-24 cm2. Cross sections can be interpreted as a measure of the relative probabilities of different kinds of events. A high cross section corresponds to a highly probable event. A low cross section corresponds to a rare one.
Let's say you have initial particles which interact in a process called resonant scattering, and then decay into final particles.
A + B → R → C + D
For instance, A and B could be an e+e- or quark pair. R could be a W+, W-, or Z0.
For simplicity, assume spinless particles. The partial wave expansion of a scattering amplitude is
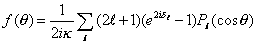
f([theta]) = (1/2ik)[summation over l](2l + 1)(e2i[delta]l -1)(Pl (cos [theta])
where k is the wavenumber which is the magnitude of the center of mass three momentum, and δl is the change in phase at the lth partial wave. "l" is lower case L. Again, I'm going to skip the algebra, but you eventually get the following relation for the cross section.
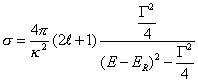
[sigma] = (4[pi]/k2) (2l + 1) (([gamma]2/4)/((E - ER)2 + ([gamma]2/4))
where σ is the cross section, E is the total energy of the scattering particles, ER is the energy of the resonance, and Γ measures the rate of change of δl near the resonance. The above equation describes a curve called a Briet-Wigner resonance. Γ is the full width at half maximum.
Let's look at a more realistic case taking into account spin, color charge, and several final particles.
A + B → R → C + D + E…
The cross section is
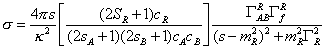
[sigma] = (4[pi]s/k2)[(2SR + 1)cR)/((2sA + 1)(2sB)cAcB)][([gamma]ABR[gamma]fR)/((s - mR2)2 + mR2[gamma]R2)]
where particles A and B scatter through resonance R, s is a Lorentz scalar variable, sA is the spin of A, sB is the spin of B, SR is the spin of the resonance, cA is the number of color charges of A, cB is the number of color charges of B, cR is the number of color charges of the resonance, mR is the resonance mass, ΓABR is the partial width for the reaction AB → R, and ΓfR is the partial width for R → final particles.
In electromagnetism, there exists a phenomenon called superconductivity. In the strong force, there exists an analogous phenomenon called color superconductivity. Superconductivity can only take place at low temperatures. Color superconductivity can only take place at very high pressures. The condensate is invariant only if you rotate color and flavor together which is called Color-Flavor Locking. Eight Goldstone bosons become the longitudinal components of the gluons which therefore become massive. At sufficiently high baryon densities, a nuclear matter will evolve to a quark matter. The attractive force mediated by one-gluon exchange or by instantons triggers the pairing instability and a color superconductor will be formed below a certain temperature. This phase of the nuclear matter may be found inside the core of a cold neutron star.
Here is a description of the Standard Model from the point of view of group theory.
Despite the enormous success of the Standard Model, it leaves many unanswered questions. There are many aspects of the Standard Model for which we would like a better explanation, and that point the way to possible extensions of the Standard Model.
The Standard Model has three different gauge groups and three coupling constants. It would be good if you could have a more unified gauge group, and understand the origin of the coupling constants. You should be able to predict sin2 θw and the color gauge coupling αs. These problems are addressed in grand unification. Why are left-handed fermions assigned to doublets, and right-handed fermions to singlets? Why are there three generations? Why do the masses exhibit a hierarchal pattern? The chirality of the fermions has to be put in by hand. The Higgs boson is the most obscure aspect of the Standard Model. You would hope that a more fundamental theory would explain the quantization of electric charge. Why is the electric charge of a down quark exactly 1/3 that of an electron? In grand unified theories, charge quantization follows automatically. Of course, ultimately we would like to include gravity in a fundamental theory of particle physics. Why is gravity so much weaker than the other forces?
Here is a list of some possible extensions of the Standard Model.
1. Axions, U(1) x SU(2) x SU(3) x U(1)PQ Explains strong CP-violation. Predicts axion.
2. Majorons, familons, U(1) x SU(2) x SU(3) x U(1)B - L This allows for small neutrino Majorana masses or possible quark mixing. Predicts majorons and familons.
3. Left-right symmetric models. Explains the origin of parity, CP-violation, quark mixing, possible small neutrino mass. Predicts new gauge bosons, heavy Majorana right-handed neutrino.
4. Supersymmetry, U(1) x SU(2) x SU(3) x SUSY Explains the hierarchy problem, Higgs mass, can possibly extend to gravity. Predicts supersymmetric partners.
5. Technicolor, U(1) x SU(2) x SU(3) x Ghypercolor Explains the hierarchy problem, Higgs mass. Predicts low mass neutral and charged Higgs bosons.
6. Grand Unified Theories, SU(5), SO(10), E8, etc. Explains unification of gauge couplings. Predicts proton decay, neutron-antineutron oscillations.
7. Kaluza-Klein, Unifies gauge and equivalence principle. Attempts to unite gravity with other forces. Assumes existence of higher dimensions.
8. Superstrings, Unification of gravity with other forces in a locally supersymmetric higher dimensional theory. Explains fermion generations.
I'm going to briefly discuss the simplest grand unified theory, or GUT, which is SU(5). Howard Georgi and Sheldon Glashow invented the SU(5) model in 1974. It is possible to construct models which unify quarks and leptons, and which also unify the electroweak and strong force. Just as SU(2) is based on the doublet, SU(5) is based on the pentuplet, or 5-component object.

The top two are the SU(2)Ldoublet. The bottom three are the color triplet [dL bar]. Imagine the generators are matrices where the sum of the diagonal elements is zero. The particles from one family are contained in a mixture of these.
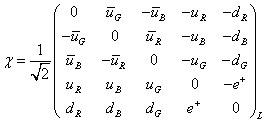
The Higgs sector, in which φ is a 5 x 5 matrix, acquires the following vacuum expectation value.
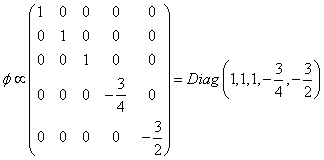
The charges of the particles in one SU(5) pentuplet add up to zero.
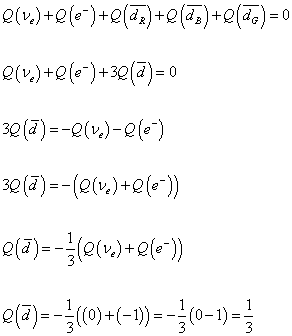
Q([nu]e) + Q(e-) + 3Q([d bar]) = 0
Q([d bar]) = -(1/3)(0 -1) = 1/3
The fractional charge of the quarks is related to the number of colors. Such an embedding of quarks and leptons into one simple group explains why the charge of the electron is of equal magnitude and opposite sign from that of the proton. It explains why charge is quantized, and why the hydrogen atom is electrically neutral.
The SU(5) model also explains the scaling of the coupling constants, and predicts they converge at some high energy scale. The SU(5) model also enables you to predict sin2θw.
An SU(n) theory has n2 - 1 gauge bosons. Thus SU(5) has 52 - 1 = 24 gauge bosons. Twelve are the same as the Standard Model, which are the photon, three intermediate vector bosons, and the eight gluons. 1 + 3 + 8 = 12. There are also twelve new ones. They are an SU(2) doublet of color triplets and their antiparticles.
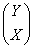
The X boson has an electric charge of -4/3, and the Y boson has a charge of -1/3. They each come in the three colors, red, blue, green, so that’s six particles. Then you have their antiparticles, which gives you a total of 12 new gauge bosons. The next simplest GUT is SO(10) which predicts a total of 45 gauge bosons which include the 24 in SU(5). The exchange of X and Y allows reactions that are not possible in the Standard Model.
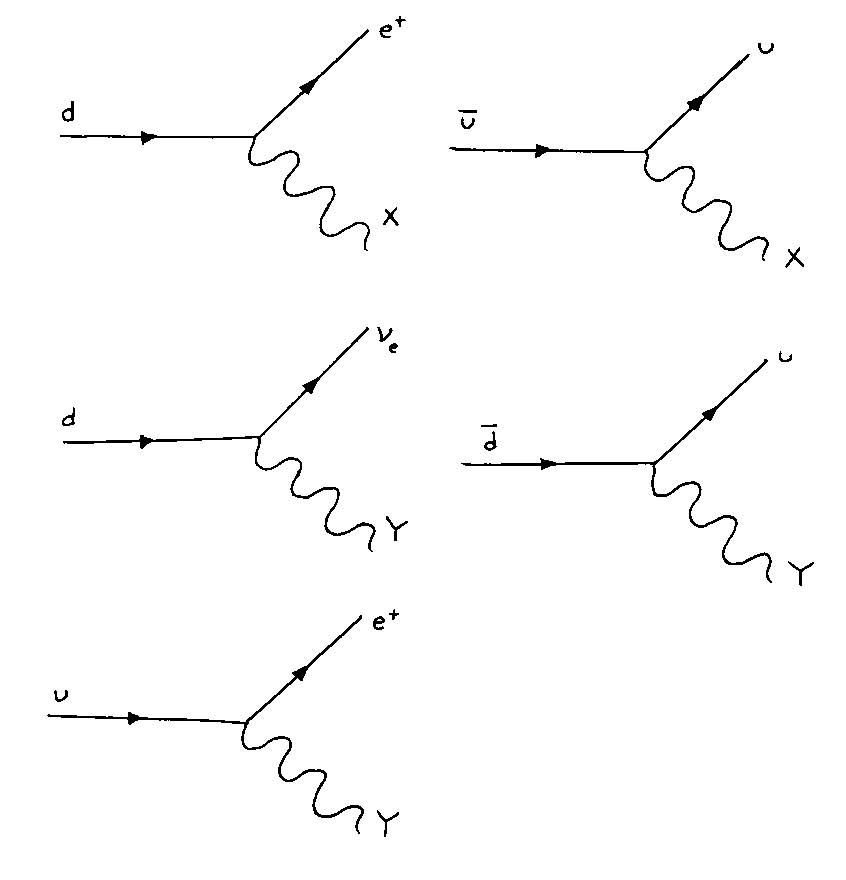
These reactions allow proton decay.
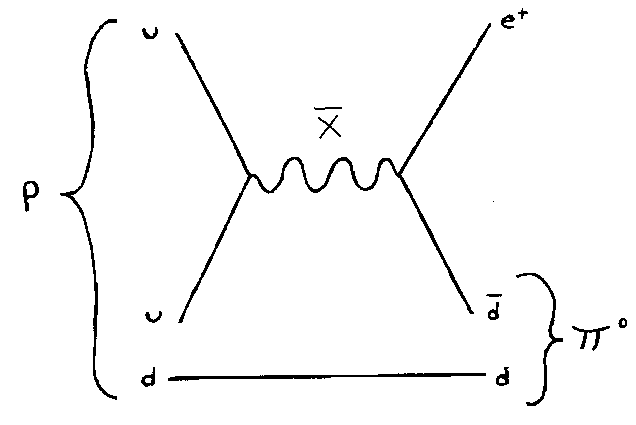
According to SU(5), the proton would have a lifetime of 1030 years, which has already been ruled out by experiment. However, other grand unified theories, such as SO(10), predict longer proton lifetimes. Also, if you take SU(5) grand unified theory, and combine it with supersymmetry, it predicts a lifetime of 1032 - 1033 years, which is not inconsistent with current experimental data.
Up until now, we have assumed that the symmetry of the S-matrix involved only commutators. If you allow both commutators and anticommutators, you have supersymmetry. It's an extension of Poincare symmetry by anticommuting spinor generators. This is a weakening of the assumptions of the Coleman-Mandula theorem which says that the only allowed symmetries of the S-matrix are Poincare invariance, internal global symmetries related to conserved quantum numbers, and the C, P, and T symmetries. Supersymmetry was proposed independently by Gol’fand and Lichtman in 1971, Volkov and Akulov in 1972, and Wess and Zumino in 1974. The ultimate result is an operator that changes bosons to fermions, and the conjugate operator that changes fermions to bosons.
Q | b > = | f >
Obviously, supersymmetry is not an unbroken symmetry but it could be a broken symmetry. According to supersymmetry, every particle has a supersymmetric partner that has a spin that is ½ less. The partners of fermions begin with "s-". The partners of bosons end with "-ino". The supersymmetric partner of the electron is the selectron which has spin 0. The supersymmetric partner of the photon is the photino which has spin ½. The other quantum numbers are unchanged.
Just as with the fermions of the Standard Model, supersymmetry allows for the partners to have arbitrary masses, but does not predict the masses. To calculate in supersymmetry, you just take the Feynman rules from the Standard Model, and replace the particles with their supersymmetric partners, keeping the coupling constants the same. Supersymmetry allows the following vertices.
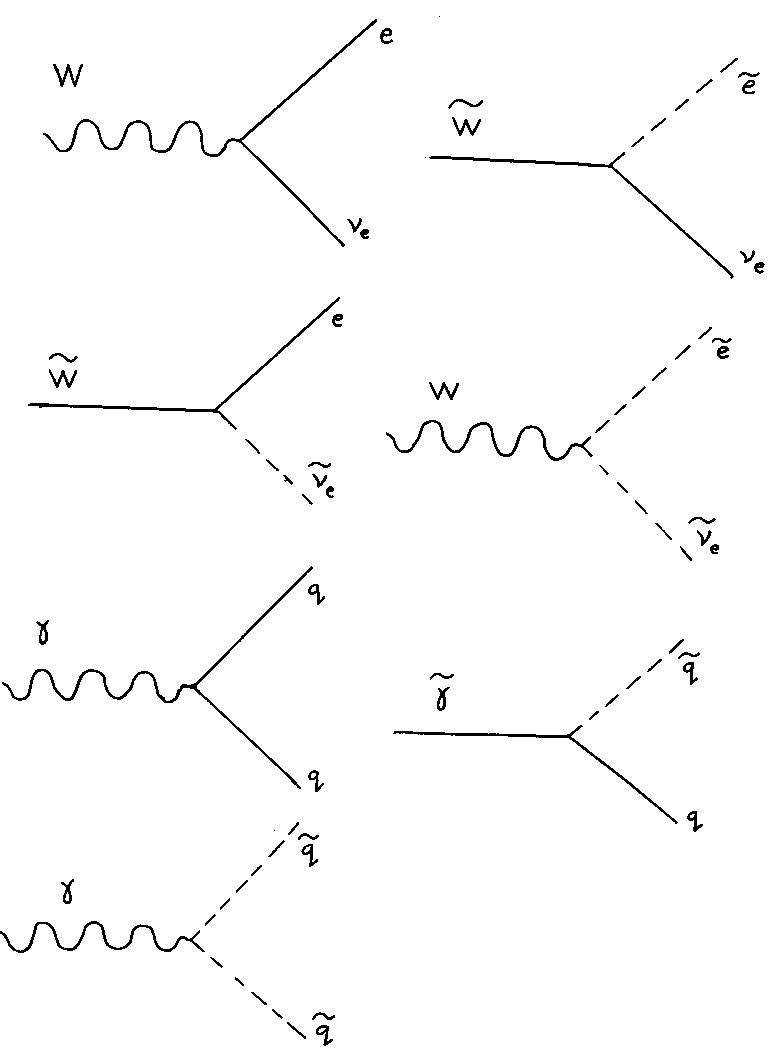
In supersymmetry, particles have a quantum number called R-parity. The particles we know about have even R-parity, and their superpartners have odd R-parity. Supersymmetric partners will be produced in pairs starting from normal particles. The decay of supersymmetric partners will contain at least one supersymmetric particle. The lightest supersymmetric particle will be stable. It's often assumed to be the photino which is a candidate for dark matter.
The masses of the elementary particles are at an energy scale much lower than the GUT scale, 1014 GeV, or the Planck scale, 1019 GeV. You would expect that the self-energy due to virtual particles would drive up the masses. You can solve this by fine-tuning the parameters but in that case, they have to be fine-tuned to 26 decimal places which is unacceptable. This is called the hierarchy problem, and supersymmetry provides a solution. In supersymmetry, the contribution to the mass from every virtual particle would be exactly cancelled by an identical opposite contribution from its superpartner. The effects from the successive loop diagrams from bosons and fermions are exactly opposite and cancel out. This would keep the masses of the particles down to the experimentally measured values despite the large gap between the electroweak energy scale and the GUT scale. Also, it would keep the Higgs mass down to about 1 TeV. Much higher would violate unitarity. Therefore, the supersymmetry breaking scale is expected to be around 1 TeV. This predicts that the supersymmetric partners, as well as the Higgs, should be around that range, which will be accessible to the Large Hadron Collider at CERN. Also, if supersymmetry were an unbroken symmetry, which it obviously is not, these contributions to the vacuum energy from the equal number of bosons and fermions would exactly cancel out at all energy scales, and we would have no vacuum or zero point energy. However, supersymmetry is obviously not an unbroken symmetry.
In grand unified theories, the coupling constants get closer together and almost converge at higher and higher energies, which is the same thing as shorter and shorter distances, or farther back in time as you get closer and closer to the Big Bang. This is indirect evidence in favor of grand unified theories. Unfortunately, in grand unified theories, they get closer together but don’t actually converge. However, if you combine grand unified theories with supersymmetry, the coupling constants do exactly converge. This is another benefit of supersymmetry.
Throughout this paper, I have discussed three of the four forces, which are electromagnetism, the strong force, and the weak force. However, I have barely mentioned the fourth force, which is gravity. It is very difficult to come up with a gauge theory of gravity because in general, the infinities are non-renormalizable. However, we have finally achieved this with string theory. Up until this point, we have assumed that fundamental particles are zero-dimensional points. String theory is based on the premise that instead particles are one-dimensional line segments. At energies far below the Planck mass, 1019 GeV, you can’t resolve distances as short as the Planck length, 10-35 m, which is the typical length of the strings, which is why for most purposes, you can approximate them as point particles. If the two endpoints of a string join to form a little loop, it's called a closed string. If not, it's called an open string. If the endpoint of an open string is fixed, it’s called a Dirichlet boundary condition. If it’s free to move, it’s called a Neumann boundary condition. They could be fixed in some dimensions but not others. In more recent theories, if the endpoint of an open string is fixed, the thing it’s fixed to is called a D-brane.
String theory was originally invented in the early 1960’s by Gabriele Veneziano, and was applied to hadrons as an attempt to explain the strong force. In 1974, John Schwarz and Joel Scherk realized that string theory included a massless spin-2 particle that could be identified with the graviton, thus raising the possibility of uniting gravity with the other forces.
The reason gravity is non-renormalizable is because of the sharp corners at the vertices of the Feynman diagrams. However, in string theory, the Feynman diagrams are three-dimensional diagrams of tubes instead of lines, and are smooth without corners. This allows gravity to be renormalizable. If you combine supersymmetry with string theory, you have superstring theory. In non-supersymmetric string theory, there are 26 dimensions. In superstring theory, there are 10 dimensions, one time dimension, and nine spatial dimensions. The ones we don't see are compactified on a type of space called a Calabi-Yau manifold. There are five types of string theory, which are Type I, Type IIA, Type IIB, and two heterotic strings, which have SO(32), and E8 x E8 symmetry respectively. Type I is an open string theory, and the rest are closed string theories. Type I has SO(32) symmetry. Type IIA and IIB do not have gauge symmetry. Type IIA is parity conserving, in contradiction to reality, although it can be made parity violating through compactification. When a string vibrates or oscillates in different ways, it appears like different particles. On heterotic strings, the vibrations moving in one direction are non-supersymmetric, and those moving in the other direction are supersymmetric, instead of both being supersymmetric. For a while, the E8 x E8 heterotic string compactified on a Calabi-Yau manifold, appeared to be the best hope since it produced a low-energy effective theory that matched a supersymmetric extension of the Standard Model.
It now appears that all the different versions of string theory are actually just different manifestations of a more fundamental theory called M-theory. There is also another theory that has 11 dimensions that in addition to the five string theories, also reduces to the underlying M-theory. Unfortunately, this 11-dimensional supergravity theory is also often called M-theory. It should be emphasized that the 11-dimensional supergravity theory is not any more fundamental than the five string theories, but they are all different manifestations or solutions of a fundamental theory usually called M-theory.