In 1911, Dutch physicist Heike Kamerlingh Onnes was astonished to find that the electrical resistance of mercury vanished below 4.2 Kelvin. Electrical resistance in metals is caused by the scattering of the conduction electrons by the impurity atoms. Obviously electrons repel each other. Let's say an electron passes near a positive ion. The attraction between them might slightly modify the vibration of the ion. This in turn could interact with a second electron nearby which will also be attracted to the ion. The net effect of these two interactions will be an apparent attractive force between the two electrons. The attraction is obviously very weak. In 1956, Cooper showed that if there was an attractive interaction, however weak, the lowest energy state of the system at T = 0 K would be one in which the electrons were paired. The pairs are therefore called Cooper pairs. If you have a pair of electrons, they can only be scattered if the energy involved is sufficient to break it up into single electrons. If less energy than that is available, they can not be scattered, and you have zero resistivity. The general theory of superconductivity was proposed by Bardeen, Cooper, and Schrieffer in 1957, and is called the BCS Theory.
Tc is the highest temperature where the thermal energy is low enough to allow pairs to exist. As you decrease the temperature, more pairs exist. The lower the temperature, the larger the fraction of electrons that are bound up in pairs. There are 25 elements that become superconductors. The lowest Tc is for tungsten and is .01 K. The highest Tc for an element is for niobium and is 9 K. The highest established Tc is for a ceramic called yttrium-barium-copper oxide, or Y-Ba-CuO, and is 90 K. There have been reports of superconductivity existing at temperatures as high as 125 K. For a single crystal of material, the range over which the resistivity drops to zero is much less than for larger impure samples. The zero resistance is only in regard to direct current. For alternating current, the superconductor does have resistance, but at low frequencies, it's very small.
The normal resistance of a superconductor can be restored if a magnetic field greater than Bc is applied to it. Bc = Bo{1-(T/Tc)2} where Bo is a constant unique to the substance. If Tc is around 1 K, Bo would be about .01 tesla. For the highest Tc, it's about .1 tesla. Associated with an electric current is a magnetic field, so if a superconductor carries a current such that the field it produced, plus any other external field, is equal to Bc, then the resistance is restored. If a magnetic field less than Bc is applied to the superconductor, a current will be induced in a direction that will oppose the effect of the applied field. The field generated by this current will exactly cancel the magnetic field you're applying, so the net magnetic field is zero. The induced current is in a surface layer where the applied magnetic field is not exactly canceled. If the external field is increased, then when it reached Bc, the persistent currents will die out and the internal magnetic field will be the same as the external magnetic field. The fact that the internal magnetic field goes to zero when the external magnetic field is below Bc is not the result of zero resistivity but an additional property called the Meissner effect. A superconductor acts as if it has a magnetic moment.
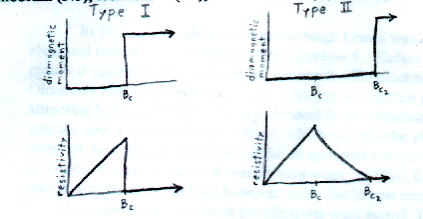
There are two types of superconductors, simply called Type I and Type II. In Type I, the transition between normal and superconducting is very abrupt. In Type II, it's more gradual. Most superconducting elements are Type I. Most alloys, and also elements niobium (Nb), technetium (Tc), and vanadium (V), are Type II.

The circulating currents increase the free energy and the electron pairing decrease it. Usually these compensate exactly. In Type I materials, near the surface, the circulating currents have a greater effect than the electron pairing and so there is positive surface energy. In Type II materials, near the surface, the electron pairing has a greater effect than the circulating currents and so there is negative surface energy. These may cause the observable characteristics of the materials.
There are exotic superconductors, such as buckyball superconductors, etc. Superconductivity, unlike many things such as superfluidity etc., has enormous practical application. I couldn't even make a list of it's uses in technology. However, this is not a panacea for losing money due to electrical resistance when transmitting electricity through wires in general because of the expense in keeping the temperature low enough for superconductivity to exist.
The discovery of superconductivity was in part the result of the study of the properties of gases at low temperatures. During the second half of the nineteenth century, scientists were developing methods to condense gases with lower and lower boiling points. Carbon dioxide was first frozen by Michael Faraday in 1845. Air, mostly nitrogen and oxygen, was liquefied independently by Raoul Pictet and Louis Paul Cailletet in 1877. In 1892, James Dewar invented the Dewar flask, which was a very effective tool to insulate the cold liquids. The Dewar flask uses two silver-coated glass walls separated by a vacuum to insulate its contents. James Dewar also liquefied hydrogen in 1898. Helium was the only gas which had not yet been liquefied.
Heike Kammerlingh Onnes, chair of experimental physics at the University of Leiden, was the first to liquefy helium. He was studying the behavior of gases at low temperatures, basing his work on the theories of his friend Johannes van der Waals. In 1907, Onnes calculated that helium would liquefy at about 5 Kelvins. On July 10, 1908, Onnes produced the first sample of liquid helium, with a boiling point of 4 Kelvins.
Onnes then began to investigate the electrical resistances of metals at low temperatures. This was a very controversial topic of research at the time. The three most widely accepted theories predicting resistivity at extremely low temperatures were those of Matthiessen, Lord Kelvin, and Dewar. Dewar predicted that resistivity would simply approach zero as absolute temperature approached zero. According to this theory, zero resistivity would not be possible from a practical point of view, as it is impossible to cool something down to absolute zero. Lord Kelvin predicted that resistivity would reach a minimum and then increase with decreasing temperature, as the electrons froze to the atoms. Resistivity would approach infinity as absolute temperature approached zero. Matthiessen predicted that resistivity would level off as absolute temperature approached zero, because resistivity due to impurities would dominate.
The Matthiessen prediction was based on a theory developed by Paul Drude and Hendrik Lorentz in 1900. Drude and Lorentz said that a perfect crystal of metallic solid would conduct electricity without any resistance. The two major sources of resistance are temperature and imperfections in the crystal structure. The higher the temperature, the more the atoms are vibrating in their crystal lattice, and the more resistance there is to the movement of electrons.
For higher temperatures, the resistivity due to temperature is more significant than resistivity due to defects. But as temperature decreases, so does resistivity due to temperature. The resistivity due to defects is not affected as much by decreasing temperature, so when the resistivity to temperature becomes insignificant, the majority of the resistivity of a metal is due to the defects in the crystal structure. This is what would cause the leveling off of resistivity as temperature approaches zero.
Using liquid helium to cool the metal samples, Onnes investigated the resistivities of gold and platinum, and found that they did in fact level off at extremely low temperatures, due to the impurities. Mercury, which could be distilled and purified to a much higher degree than platinum or gold, was then used in the experiments. When the mercury was cooled to about 4 Kelvins in 1911, electrical resistivity was found to abruptly drop to zero. These results were checked and rechecked, and the discovery was finally announced. Heike Kamerlingh Onnes received the 1913 Nobel Prize in Physics for his discovery.
Soon after Onnes's discovery of superconductivity in mercury, other metals were found to superconduct. Tin and lead were found to have a critical temperatures of 3.7K and 7.2 K, respectively. It was also discovered that impurities had little effect on the superconductive properties of a material. It was not necessary to distill mercury for it to superconduct. Superconducting alloys were found in 1931, also at the Kamerlingh Onnes Laboratory.
According to James Clerk Maxwell's laws, a perfect conductor would not allow any change in magnetic flux. Any change in magnetic flux would induce eddy currents in the perfect conductor which would produce a magnetic flux opposite to the change in magnetic flux which was originally introduced. If a superconductor were a perfect conductor, it should behave the same way. A material becomes superconducting when its temperature drops below the critical temperature. So when the temperature is higher than the critical temperature, the material is not a perfect conductor, but when the temperature is lower than the critical temperature, the material superconducts.
Let's say you have a perfect conductor with zero magnetic flux inside it. If a permanent magnet were brought near the perfect conductor, the magnetic flux inside the conductor would remain zero, due to the induced currents. The magnetic field from the induced currents would oppose the magnetic field of the permanent magnet. If this permanent magnet had a magnetic field strong enough to support its own weight, it could be levitated above the perfect conductor.
Now let's say you have a material at a temperature above its critical temperature. It has a resistivity greater than zero, so when a permanent magnet is brought near it, the magnetic flux can penetrate the material. If the material were then cooled to a temperature below its critical temperature, and became perfectly conducting, the magnetic flux would be trapped inside it. No magnetic field opposite the magnetic field of the permanent magnet would be present, and it would not be possible to levitate the magnet.
In Berlin in 1933, an experiment was done by Walther Meißner and Robert Ochsenfeld to test whether superconductors behaved the way Maxwell's laws predicted a perfect conductor to behave. They found that a superconductor will expel any magnetic flux whether it becomes superconducting before or after the magnetic field is brought near it. A perfect conductor would resist a change in flux, while a superconductor expels any flux at all. The explanation for this is that a superconductor is not a theoretical perfect conductor as described by Maxwell's laws. A superconductor is a perfect diamagnet, a material which resists internal flux. This phenomenon is now known as the Meißner- Ochsenfeld effect, more commonly referred to as the Meissner effect.
The original elemental superconductors such as mercury, aluminum, and zinc are classified as type I superconductors. They have one critical magnetic field for any given temperature. If they are in a magnetic field that is weaker than the critical magnetic field, they have zero resistance and exhibit perfect diamagnetism. If they are in a magnetic field that is stronger than the critical magnetic field, they have resistance greater than zero, and there is flux penetration.
Type II superconductors have two critical magnetic fields (Bc1 < Bc2). Type II superconductors behave the same way type I superconductors do for B < Bc1, and also behave as normal materials for B > Bc2. However, for a magnetic field between Bc1 and Bc2, type II superconductors have a unique property which type I superconductors do not have. They have zero resistance, but allow partial flux penetration. This was discovered in 1957 by Soviet physicist Alexi Abriksov.
Type II superconductors are alloys and compounds, with the two exceptions of niobium and vanadium. When the magnetic field is between Bc1 and Bc2, the type II superconductor is said to be in the vortex state. In the vortex state, there are several cores of normal material, surrounded by material in the superconducting state. Quantized supercurrents surround each core, creating exactly one quantum of magnetic flux per core. Increasing the magnetic field increases the number of vortices, and when no more vortices can fit into the superconductor, the material becomes nonsuperconducting.
As many other quantities in physics are quantized, so is magnetic flux. The magnetic flux quantum is value of magnetic flux which all other quantities of magnetic flux are an integer multiple of. When the magnetic flux quantum was actually measured, it was found to be h/(2e) rather than h/e, where h is Planck's constant and e is the elementary charge. This proportionality to the reciprocal of twice the elementary charge indicated that superconductivity had something to do with electron pairing.
Superconductivity still has not been totally explained. Most of the research done has been experimental rather than theoretical. For example, the formula for critical magnetic field as a function of temperature:
Bc(T) = Bc(0K) [1-(T/Tc)2]
is an empirical formula based on experimental data rather than theoretical prediction. The BCS Theory, however, developed in 1957 by John Bardeen, Leon Cooper, and Robert Schrieffer, does establish a model for the mechanism behind superconductivity. Bardeen, Cooper, and Schrieffer received the Nobel Prize in Physics in 1972 for their theory.
It was known that the flux quantum was inversely proportional to twice the charge of an electron, and it had also been observed that different isotopes of the same superconducting element had different critical temperatures. The heavier the isotope, the lower the critical temperature is. BCS theory states that in a superconductor, electrons form pairs. As the first electron moves through the crystal lattice, it pulls the nuclei of the atoms in the superconductor toward it. The second electron, rather than experiencing a backward force from the first electron, experiences a forward force from the positively charged nuclei in front of it. This is how the electrons stay together rather than being repelled as they move through the lattice. A pair of electrons moving through the lattice of a superconductor is referred to as a Cooper pair, after Leon Cooper. The forces on the nuclei of the atoms in the lattice by the electrons cause vibrations referred to as lattice vibrations, or phonons. The idea of electron-phonon interaction was actually first proposed in 1950 by Herbert Frohlich, but it took until 1957 for the necessary experiments to be completed and a formal theory to be written.
The lattice vibrations are very similar to the oscillation of a spring, which is also caused by the stretching and contracting of the bonds between the atoms in the spring. The critical temperature of an isotope can be predicted by the formula
Tc = K / M[alpha]
where K is a constant, M is the isotopic mass, and α is the isotope-effect exponent. Theoretically, according to BCS theory, α should have a value of about 1/2. The resonant frequency of a simple mass-spring system is also proportional to m^(-1/2). Some examples for values for α are 0.32 for cadmium, 0.61 for thallium, and 0.00±0.05 for Zirconium. These experimental values for the isotope-effect exponent are not exactly 1/2 because the forces between the electrons also affect a. It is interesting that thallium has a value of 0.00 for α. The BCS theory cannot explain this. Although the BCS model is a brilliant theory describing the mechanism for superconductivity, it also cannot explain which materials are superconductors and which materials are not.
The reason metals with low resisitivities at room temperature, such as copper, silver, and gold, are not superconductors and metals with higher resistivities at room temperature, such as mercury, tin, and lead, are superconductors is because of the lattice vibrations. When a material is warm, the lattice is vibrating somewhat randomly due to the thermal energy. The more the lattice is vibrating, the more the electrons traveling through the lattice will be slowed down by the vibrating atoms in the lattice. Materials with lattices which vibrate easily generally have higher resistivities at room temperature, while materials with lattices which do not vibrate easily generally have lower resistivities at room temperature. However, at very low temperatures, the Cooper pairs can move more easily through the materials with lattices which are more susceptible to vibration. In 1986, materials which are actually insulators at room temperature were found to be superconductors. These superconductors have much higher critical temperatures than the traditional superconductors, and are therefore referred to as high-temperature superconductors. Many are above 77K, the boiling temperature for nitrogen.
The first high-temperature superconductor was discovered in 1986 by Karl Alex Müller and Johannes Georg Bednorz at the IBM Research Laboratories in Zürich, Switzerland. Up until 1986, the highest known critical temperature was 23K for Nb3Ge. Müller had already observed superconductivity in certain oxides, known as perovskites, for about two years before the discovery of the first high-temperature superconductor, but the critical temperatures were not any higher than the critical temperatures for the metallic superconductors. In 1986, Müller and Bednorz heard that a sample of lanthanum barium copper oxide had been produced by Claude Michel, L. Er-Rahko, and Bernard Raveau at the University of Caen in France. The French scientists were not researching superconductivity, but Müller and Bednorz recognized that the compound was a possibility for a high temperature superconductor. They quickly produced their own samples of lanthanum barium copper oxide (La1.85Ba0.15Cu1O4) and found the critical temperature to be about 30K. This was a significant breakthrough. A new class of superconductors had been found. Müller and Bednorz received the Nobel Prize in Physics in 1987 for their discovery.
Soon after the discovery of superconductivity in lanthanum barium copper oxide, researchers around the world began investigating superconductivity in the perovskites in search for a room temperature superconductor. In 1987, a group of researchers lead by C. W. Paul Chuat the University of Alabama in Huntsville, working together with another group at the University of Houston, discovered a compound which superconducts above 77K, the boiling point of nitrogen. It was known that the original lanthanum barium copper oxide superconductor's critical temperature increased as pressure was applied, so the researchers substituted various transition metals for lanthanum and tried different ratios of elements in the compound to try to simulate higher pressures. When yttrium was substituted for lanthanum in a ratio of 1:2:3 with barium and copper (YBa2Cu3O7-Δ, where Δ is variable), the critical temperature was measured to be 90K. Liquid nitrogen, which is easier to obtain, easier to work with, and much cheaper, could be used instead of liquid helium. Today, critical temperatures are approaching 200K as scientists continue searching for room temperature superconductivity.
In superconductivity, you have two electrons in the same quantum state. These are the Cooper pairs. In superfluidity, you have two helium atoms in the same quantum state. In a Bose-Einstein condensate, you have a large number of atoms in the same quantum state. Therefore these three effects are related. They are all examples of quantum effects being observed macroscopically. Superconductivity, superfluidity, and the Bose-Einstein condensate are manifestations in solids, liquids, and gases respectively, as well as in one, two, and three dimensions respectively.
In electromagnetism, there exists a phenomenon called superconductivity. In the strong force, there exists an analogous phenomenon called color superconductivity. Superconductivity can only take place at low temperatures. Color superconductivity can only take place at very high pressures. The condensate is invariant only if you rotate color and flavor together which is called Color-Flavor Locking. Eight Goldstone bosons become the longitudinal components of the gluons which therefore become massive. At sufficiently high baryon densities, a nuclear matter will evolve to a quark matter. The attractive force mediated by one-gluon exchange or by instantons triggers the pairing instability and a color superconductor will be formed below a certain temperature. This phase of the nuclear matter may be found inside the core of a cold neutron star.