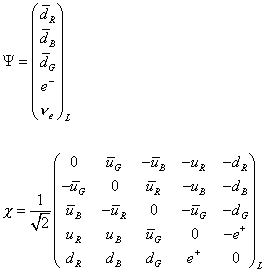
In this paper, I assume the reader has previously read my other papers on tensors, Lagrangians, and the Standard Model. In this paper, I discuss grand unified theories, supersymmetry, and string theory. I briefly mentioned each of these at the end of my paper on the Standard Model, so I assume the reader has some vague notion of what they are. The Standard Model is a remarkably successful theory. So far, all experimental data is consistent with the Standard Model. However, no one thinks it's the final theory of nature, since there is so much about it that is unexplained. There are many parameters that have to be added by hand. Why are there three families or generations? Why is charge quantized? The most obvious extension of the Standard Model is grand unification, also called grand unified theory or GUT. This is an attempt to continue the success of the ideas and methods of the Standard Model itself. In the Standard Model, the electroweak theory undergoes spontaneous symmetry breaking, and becomes the electromagnetic and weak force. It's easy to imagine that some similar method of symmetry breaking of a larger group could give rise to the electroweak and strong gauge groups. Whereas in the Standard Model, the electroweak group SU(2) x U(1) and the QCD group SU(3) are just linked together to form SU(3) x SU(2) x U(1), in grand unified theories, they are all embedded in a larger group, say SU(5). Then quarks and leptons would be placed in the same multiplet, and could be transformed into each other, so baryon number and lepton number are no longer conserved. The idea is to find some way of putting all the various of particles of the Standard Model into a set of multiplets, and write down a Lagrangian that is invariant under the operation of some group G, where G → SU(3) x SU(2) x U(1).
In 1974, Howard Georgi and Sheldon Glashow proposed the SU(5) model, which is the simplest possible grand unified theory. Let's first address the question, why is SU(5) the simplest group? There are infinitely many Lie groups that could be chosen. There is SU(n), SO(n), Sp(2n), and the exceptional groups which are G2, F4, E6, E7, and E8. The order of a group is the number of generators. The rank of a group is the number of generators that can be diagonalized simultaneously. The Standard Model is rank 4, so the group it is embedded in has to be at least rank 4. Also, we want simple groups, meaning groups that aren't products of other groups. That gives five possibilities, which are SU(5), SO(8), SO(9), Sp(8), and F4. Now, remember that the Standard Model is parity violating. The left-handed fermions are assigned to doublets, and the right-handed fermions are assigned to singlets. The operation of charge conjugation, which changes the helicity, involves complex conjugation. Real numbers are the same as their complex conjugates, a + 0i = a - 0i, so the group must accommodate complex representations. With this additional requirement, SU(5) is the only group that meets the requirements. The unitary gauge group SU(5) does admit the Standard Model gauge group as the maximal subgroup, and is an ideal candidate for unification. It is the smallest group large enough to contain the Standard Model gauge group. Later, I explain Dynkin diagrams, but suffice it to say here that if you take the diagram for SU(5), and erase the right-most dot, you get the diagram for the Standard Model.
The SU(5) group has 52 - 1 = 24 gauge bosons. Twelve are the familiar gauge bosons of the Standard Model, which are the photon, W+, W-, Z0, and the eight gluons. The other twelve gauge bosons change quarks to leptons, and vice versa. The X particles have a charge of -4/3, and the Y particles have a charge of -1/3. Each comes in three colors, red, blue, green, so that's six. Plus, you have their antiparticles, so that's twelve. The particles from one family are contained in a mixture of a 5D vector and a 5 x 5 matrix.
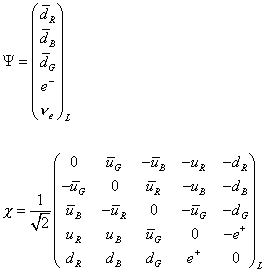
Notice that the above 5 x 5 matrix is an antisymmetric tensor. For a general SU(n) grand unification, in order to ensure the vector nature of the color gauge interactions, to have only three colors, and three anticolors, the simplest choice is to assign fermions only to antisymmetric representations. The irreducible representations will be
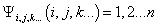
[psi]i, j, k…(i, j, k, …) = 1, 2, …n
for SU(n), antisymmetric on exchange of indices. The dimensionality of an mth rank antisymmetric tensor under SU(n) is
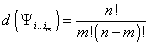
d([psi]i…im) = n!/m!(n - m)!
This has nothing to do with the dimensionality of spacetime which we're still assuming is normal 4-D spacetime. You want to have anomaly-free combinations. The anomalies Am,n associated with an antisymmetric tensor under SU(n) is
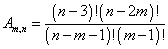
Am,n = (n - 3)! (n - 2m)/(n - m -1)! (m - 1)!
The formula for the beta function of SU(n) with fermions in [n, m] is
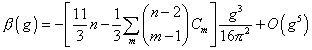
[beta][n, m] = -[(11/3)n - (1/3)[summation][doublet of n-2 m-1] Cm](g3/16[pi]2) + O(g5)
The 5D vector I gave earlier is the 5-dimensional representation, and the 5 x 5 matrix is the 10-dimensional representation. If you take both representations as left-handed, as above, so they have the same handedness, the representations are called [5 bar] + 10
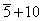
meaning the particles in the 5-dimensional left-handed representation are the antiparticles of those in the 5-dimensional right-handed representation. The 5 + 10 representation is
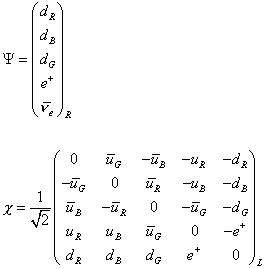
Some people list the colors as 1, 2, 3 instead of R, B, G, or convey antiparticles with a superscript c, meaning charge conjugation, instead of a bar.
You can also have a 24-dimensional representation. A Higgs scalar in the 24-dimensional representation can be used to break SU(5) down to the Standard Model. The 24-dimensional representation is also the adjoint of SU(5) which contains the gauge bosons of the unified group. The theory is specified by writing down the terms of the Lagrangian that couple these fields. The Yukawa coupling can be written down for the fermions in the [5 bar] and 5-dimensional scalar.
Remember that SU(n) has n2 - 1 generators. SU(2) has 22 -1 = 3 generators which are the Pauli spin matrices. SU(3) has 32 -1 = 8 generators which are the Gell-Mann lambda matrices. SU(5) has 52 - 1 = 24 generators. The gauge bosons are added to cancel out the effects of the generators when making the Lagrangian locally invariant. Below are the generators for SU(5). The first eight are just the Gell-Mann matrices in the upper left-hand corner with the rest zero. Matrices 21 - 23 are just the Pauli spin matrices in the lower right with the rest zero. This is similar to the fact that the first three Gell-Mann matrices are just the Pauli spin matrices in the upper left-hand corner with the rest zero. You can guess that the gauge bosons created by the generators that contain the Gell-Mann matrices or Pauli spin matrices are the familiar gauge bosons from the Standard Model.
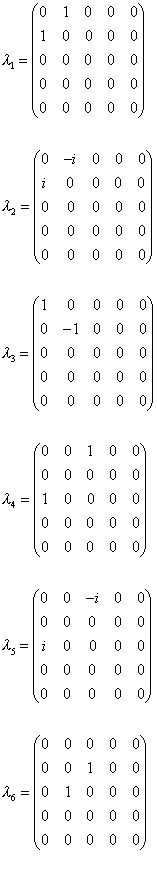
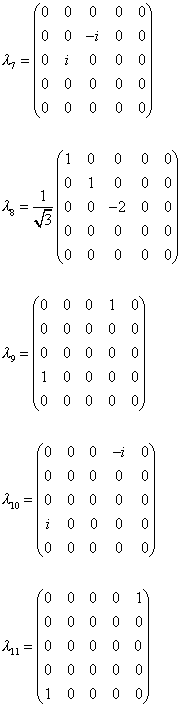
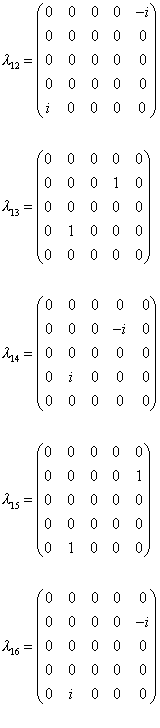

This gives the following form of the gauge boson matrix. Therefore, the gluons, which are the result of the Gell-Mann matrices, are the 3 x 3 subgroup in the upper left. The photon, W+, W-, and Z0, which are the result of the Pauli spin matrices, are in the 2 x 2 subgroup in the lower right.
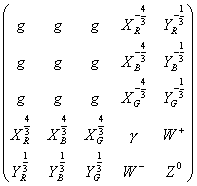
I could have included subscripts for the gluons specifying the color, which are the eight colors I listed in my paper on the Standard Model.
The fact that Standard Model fermions of different charges are accommodated into irreducible representations of SU(5) implies there is a basis for relating the charges of those fermions in the same multiplet. For instance, when we consider the electroweak doublet and the down type antiquark that lie in the same [5 bar], it implies that the action of the same diagonal hypercharge generator produces eigenvalues of their respective hypercharges. This in turn implies that charge is now quantized. Furthermore, we have the result that the normalization of the hypercharge generator is now related to the normalization of the diagonal generators of SU(2) and SU(3).
If you look at the particles in the 5-dimensional representation, their charges add up to zero. This is because, if you notice, the generators of SU(5) are all traceless, meaning of the sum of their diagonals are all zero.
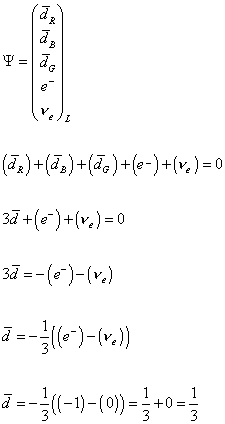
Therefore, the fact that the down quark has exactly 1/3 the charge of an electron, and the fact that hydrogen is electrically neutral, is related to the number of colors of the quarks.
In the Standard Model, you have the Gell-Mann-Nishima relation.
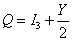
Q = I3 + Y/2
In SU(5), if we consider the SU(3) subgroup to lie in the upper left 3 x 3 subgroup, and the SU(2) to lie in the lower right 2 x 2 subgroup, then
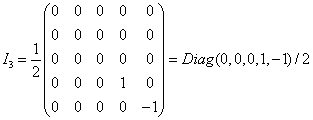
I3 = Diag (0, 0, 0, 1, -1)/2
and the hypercharge is proportional to
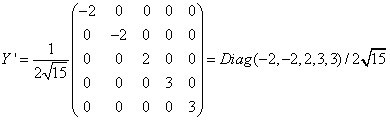
Y' = Diag (-2, -2, 2, 3, 3)/2[square root of 15]
Therefore, in order to have the correct charge assignments in [5 bar], the 5-dimensional representation, the Gell-Mann-Nishima equation is modified to
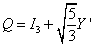
Q = I3 + [square root of 5/3]Y'
Another benefit of SU(5) grand unification is that it accurately predicts the Weinberg angle, θw, which is a measure of the ratio of the couplings g1 and g2. First, you calculate sin2 θw at the GUT scale where the symmetry holds, and then you use that to determine what it would be at our energy scale.
Write down the electric charge in terms of the SU(5) generators.
Q = I3 + cI1
where I3 is the SU(2) generator, and I1 is the U(1) generator. c is a constant. For the SU(5) generators, the covariant derivative is
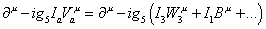
[partial derivative]u - ig5 Ia Vau = [partial]u - ig5(I3W3u + I1Bu + …)
where Va u are the SU(5) gauge bosons. There is only coupling constant g5 for all interactions.
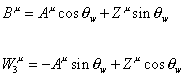
Bu = Au cos [theta]w + Zu sin [theta]w
W3u = -Au sin [theta]w + Zu cos [theta]w
Therefore you have
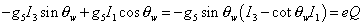
-g5I3 sin [theta]w + g5 sin [theta]w (Iw - cot [theta]w I1) = eQ
Therefore
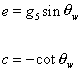
e = g5 sin [theta]w
c = - cot [theta]w
Now, you have to calculate c from the properties of SU(5). If you take any two generators Ia and Ib, and take the trace of the product, the answer is zero unless a = b. Using Tr I3 I1 = 0
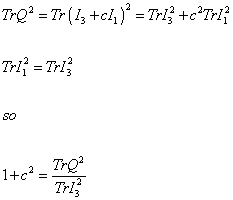
Tr Q2 = Tr (I3 + cI1)2 = Tr I32 + c2 Tr I12
Tr I12 = Tr I32
so
1 + c2 = (Tr Q2)/(Tr I32)
Using the 5-dimensional representation
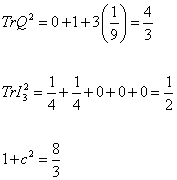
Tr Q2 = 0 + 1 + 3(1/9) = 4/3
Tr I32 = ¼ + ¼ + 0 + 0 + 0 = ½
1 + c2 = 8/3
Therefore
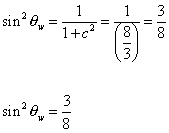
sin2 [theta]w = 1/(1 + c2) = 1/(8/3) = 3/8
However, this is the value predicted for the energy scale at which the GUT symmetry still holds. We now have to calculate it for our energy scale. From the Standard Model Lagrangian
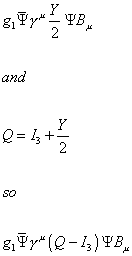
g1[psi bar] [gamma]u (Y/2) [psi] Bu
and
Q = I3 + Y/2
so
g1[psi bar] [gamma]u (Q - I3) [psi] Bu
Also, from the SU(5) Lagrangian
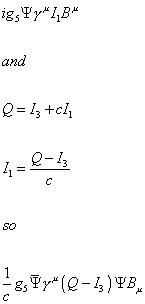
ig5 [psi] [gamma]u I1 Bu
and
Q = I3 + cI1
I1 = (Q - I3)/c so
(1/c)g5 [psi bar] [gamma]u (Q - I3) [psi] Bu
thus
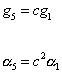
g5 = cg1
[alpha]5 = c2 [alpha]1
so at the unification scale
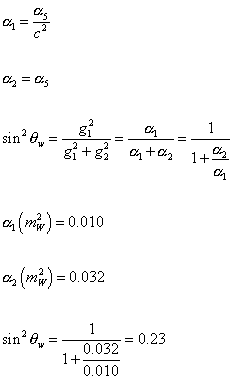
[alpha]1 = [alpha]5/c2
[alpha]2 = [alpha]5
sin2 [theta]w = g12/(g12 + g22) = [alpha] 1/([alpha]1 + [alpha]2) = 1/(1 + ([alpha]2/[alpha]1))
[alpha]1 (mW2) = 0.010
[alpha]2 (mW2) = 0.032
sin2 [theta]w = 1/(1 + (0.032/0.010)) = 0.23
Thus, as you can see, grand unified theory accurately predicts the Weinberg angle, which previously, could only be determined experimentally.
There is indirect evidence for grand unified theory. The coupling constants are not constant but in fact vary with energy. At high energies, which is the same as short distances, they get closer together. The mere fact that they change with energy should not in and of itself suggest that they converge but they do. This suggests that something special does happen when they converge, and we interpret this as the scale at which grand unified theory is broken.
A unification scale MG ~ 1016 GeV is suggested by gauge coupling unification, above which physics is described by a grand unified theory based on gauge group G. The arrival at the structure of fundamental interactions from renormalization group flow has a predecessor in the example of asymptotic freedom in deep inelastic scattering experiments, and thus gauge coupling unification is an encouraging sign that grand unified theories are a step in the right direction.
The coupling constants of the Standard Model are logarithmically varying functions of energy described by renormalization group equations of the form
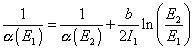
1/([alpha](E1)) = 1/([alpha](E2)) + b/(2I1) ln (E2/E1)
where
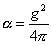
[alpha] = g2/4[pi]
and the b coefficients are
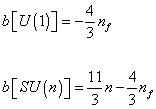
b[U(1)] = -(4/3)nf
b[SU(n)] = (11/3)n - (4/3)nf
where nf is the number of families, which is three in the Standard Model.
If you plot the coupling constants versus energy, you get
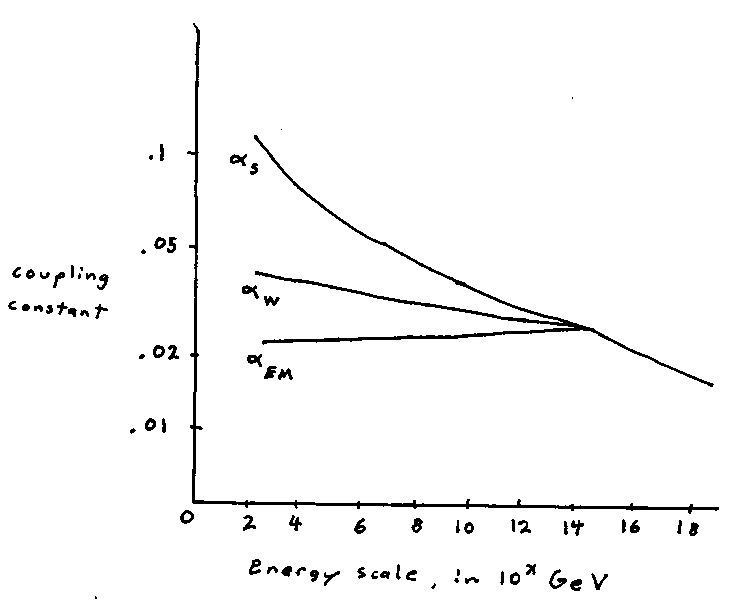
However, despite the fact the coupling constants get closer together, and almost converge, they don't actually converge. However, if you include supersymmetry, then they do actually converge.
Obviously, the symmetry of SU(5) group is broken at low energies, so we have to figure out how the SU(5) group breaks down to the SU(3) x SU(2) x U(1) group. We do this using the Higgs mechanism, similar to the breaking of electroweak symmetry. We introduce two Higgs multiplets, one belonging to the 24-dimensional representation, called φ, and the other belonging to the 5-dimensional representation, called H. The first stage breaks SU(5) down to the Standard Model, and is given by φ not being zero. The second stage breaks the electroweak, and is given by H not being zero.
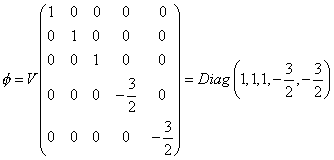
[phi] = V Diag (1, 1, 1, -3/2, -3/2)
The breakdown is along the λ24 direction. This is responsible for the first stage of symmetry breaking. The second stage is given by
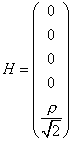
In the presence of both H and φ, the vacuum expectation value of φ changes to
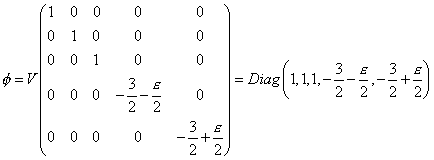
[phi] = V Diag (1, 1, 1, -3/2 - [epsilon]/2, -3/2 + [epsilon]/2)
Therefore, the masses of bosons are
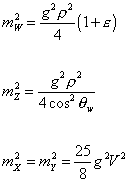
mW2 = (g2p/4)(1 + [epsilon])
mZ2 = g2p/4 cos2 [theta]w
mX2 = mY2 = (25/8)g2V2
You also have to add several Higgs multiplets to generate the fermion masses. The part of the Lagrangian that involves X and Y is
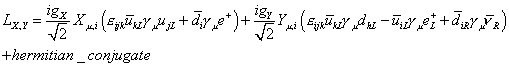
LX, Y = (igX/[square root of 2]) Xu,i ([epsilon]ijk [u bar]kL [gamma]u ujL + [d bar]i [gamma]u e+) + (igY/[square root of 2]) Yu, i ([epsilon]ijk [u bar]KL [gamma]L dhL - [u bar]iL e+L + [d bar]iR [gamma]u [nu bar]R) + hermitian conjugate
The Hamiltonian obtained for X and Y exchange for the first generation is
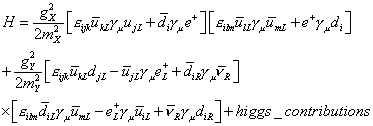
H = (gX2/2MX2) [[epsilon]ijk [u bar]kL [gamma]u ujL + [d bar]i [gamma]u e+] [[epsilon]ilm [u bar]lL [gamma]u [u bar]mL + e+ [gamma]udI] + (gY/2MY2) [[epsilon]ijk [u bar]kL [gamma]u djL - [u bar]iL [gamma]u e+L + [d bar]iR [gamma]u [nu bar]R] x [[epsilon]ilm [d bar]lL [gamma]u [u bar]mL - e+L [gamma]u uiL + [nu bar] [gamma]u dIR] + Higgs contributions
Some people call the X and Y bosons leptoquarks, since they mediate reactions that convert leptons to quarks, and vice versa, but I think this is a misleading name, since it implies they are similar to leptons and quarks. X and Y bosons are bosons, and are thus totally different from leptons and quarks, which are fermions.
The exchange of X and Y bosons allows new reactions to take place. These reactions would take place much more rarely than the Standard Model reactions because the X and Y bosons have masses on the order of the GUT scale, and thus would be very short range. It's rare that two particles would stray close enough to each other to exchange one. However, when they do, a quark can be converted into a lepton, or vice versa. Here are the vertices that can be used to construct Feynman diagrams.
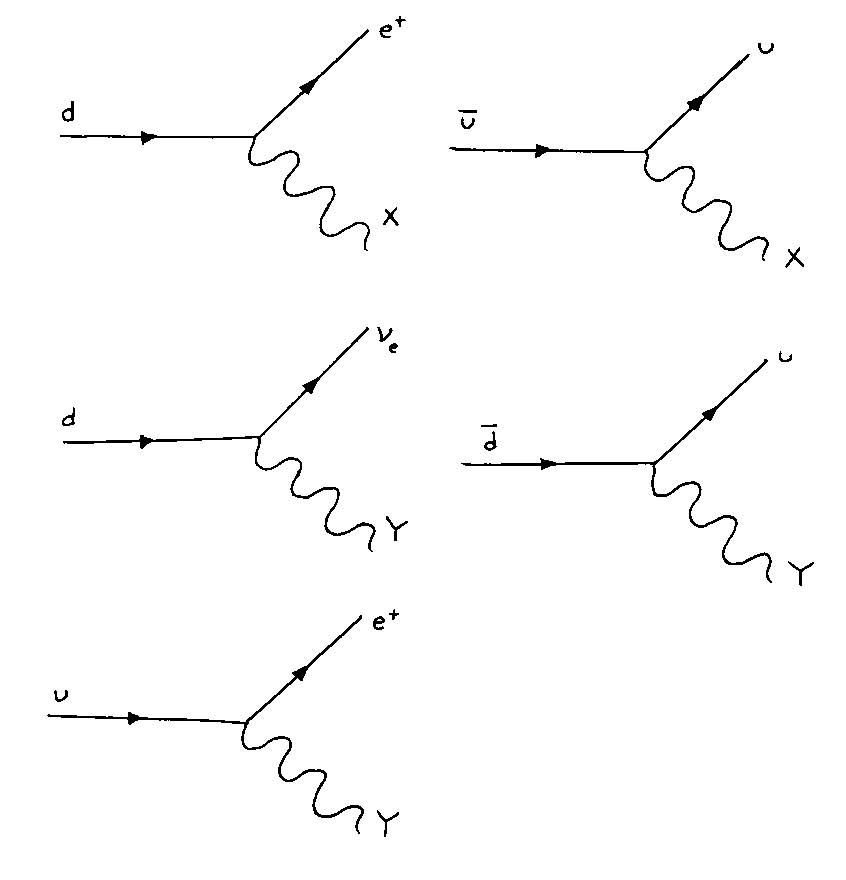
The fact that you can now convert quarks to leptons, and baryon number is no longer conserved, means that the proton is no longer absolutely stable. Here are some possible decay modes for the proton.
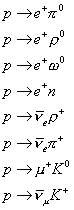
p -> e+ [pi]0
p -> e+ [rho]0
p -> e+ w0
p -> e+ n
p -> [nu bar] [rho]+
p -> [nu bar] [pi]+
p -> [mu]<+ K0
p -> [nu bar][mu] K+
The last one involves flavor mixing effects. Similarly, a bound neutron inside a nucleus can now decay, via the following decay modes.
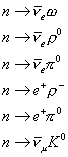
n -> [nu bar] w
n -> [nu bar] [rho]0
n -> [nu bar] [pi]0
n -> e+ [rho]-
n -> e+ [pi]0
n -> [nu bar][mu] K0
The last one involves flavor mixing effects. It should be noted that even though baryon number and lepton number are not conserved, baryon number minus lepton number, B - L, is conserved. The X and Y bosons have a definite B - L of 2/3.
The most common way for a proton to decay is by p → e+ π0
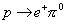
There are several different diagrams that correspond to this reaction but the most common ways for it to happen is by either of the following two diagrams.
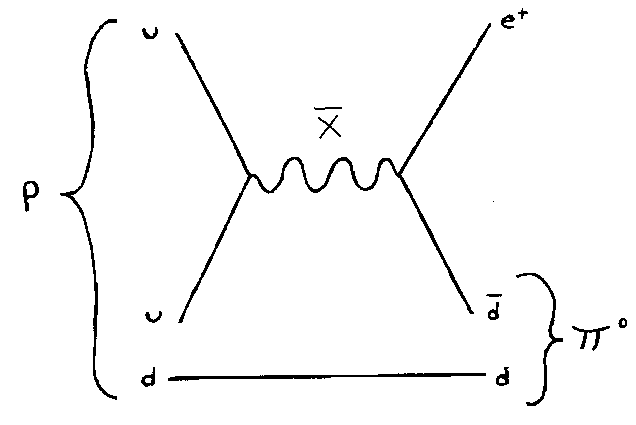
as well as
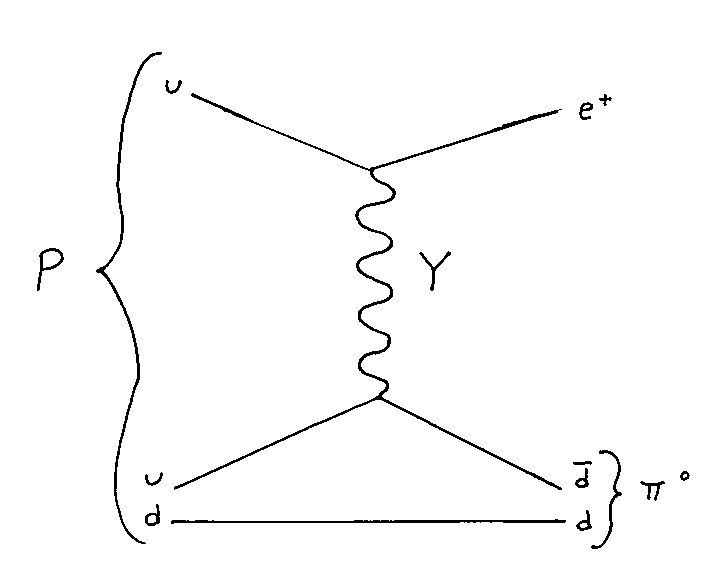
Branching ratios are a measure of what percentage of decays are by a given decay route.
p → e+ π0 would have a branching ratio of 40% - 60%.
p → e+ w would have a branching ratio of 5% - 20%.
p → e+ ρ0 would have a branching ratio of 1% - 10%.
p → [ν bar]e π0 would have branching ratio of 16% - 24%.
The cross section for p → e+ π0 is given by
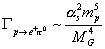
[capital gamma] ~ ([alpha]s2 mp2)/MG4
The smaller the cross section, the more rare two particles will be that close, and so the lifetime is the inverse of the cross section.
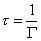
We aren't that sure of the exact value of the GUT scale, but if you plug in the common range of values, you get 1030 - 1031 years.
Since the Universe is only 13.7 billion years old, you might think it would be impossible to detect this. However, by looking at a large number of protons, you could theoretically detect this. One cubic centimeter of water contains 6 x 1023 nucleons, so a cube 10 meters on a side contains 1033 nucleons. Therefore, by looking at 10,000 tons of water, you should be able to detect proton decay. The signature of p → e+ π0 decay is photons since π0 → γ γ, and e+ gives Cerenkov radiation. The detector must be sensitive to very few photons, and the water must be so pure that a decay anywhere will be visible to the photomultiplier tubes on the walls.
Such proton decay detectors have been looking for proton decay for the past 15 years. During that time, they have been very successful at detecting neutrinos, such as from Supernovae 1987A or from the Sun, establishing the solar neutrino problem, which is strong evidence that neutrinos have mass. However, there has never been a confirmed signal of proton decay. In other words, SU(5) grand unified theory has been ruled out experimentally. Although initially disappointing, this really shouldn't be all that surprising, since SU(5) is the only the simplest possible extension of the Standard Model. I don't think anyone seriously thought that SU(5) all by itself was the final theory in physics. Higher gauge groups in grand unified theories, such as SO(10), can predict longer proton lifetimes. Also, if you combine grand unified theories with supersymmetry, it predicts a proton lifetime of 1033 years which has not been ruled out by experiment. Today, particle physicists always include supersymmetry in their models, and in that case, it would probably be impossible to confirm the prediction of proton decay. Probably the upper limit on what can be detected is 1032 years. Beyond that level, intrinsic backgrounds that look just like the signal are too frequent to allow a signal to be seen. Such backgrounds could arise from say, an upper atmosphere cosmic ray collision that produces pions, which then decay to neutrinos, followed by neutrino interactions that produce the same final signature as a real decay, and can't be separated by analysis. Since supersymmetric grand unified theories predict a proton lifetime of 1033 years, that pretty much rules out detecting proton decay as a possible way of confirming the model.
This does lead to a more general criticism of post-Standard Model physics, which is its lack of connection with experiment. From when Han Oersted noticed that an electric current deflects a compass needle in 1819, the first indication of a connection between electricity and magnetism, to the detection of the W+, W-, and Z0 bosons with the predicted masses at CERN in 1983, the progress of particle physics has been an enthusiastic rush of both theoretical and experimental advancement, inextricably intertwined, as theoretical predictions were immediately confirmed by experiment, and experimental puzzles were quickly explained by new theories. However, theory and experiment drifted apart after the detection of the W+, W-, and Z0. Of course, there have been great experimental successes of particle physics since then, such as the detection of the top quark in 1995, and the tau neutrino in 2000. However, these were still just confirmations of the Standard Model, which modern theoretical particle physics considers as quaint as Newtonian mechanics. Since then, particle physics has moved far beyond the Standard Model, into the realm of grand unification, supersymmetry, and string theory, none of which are directly experimentally testable with current technology. This has led to a totally unfair criticism of particle physics. John Baez, another physics writer on the Internet, wrote about the failure to detect proton decay, "Theoretical physics never really recovered from this crushing blow. In a sense, particle physics gradually retreated from the goal of making testable predictions into a wonderland of pure mathematics, first supersymmetry, then supergravity, then superstrings, even more elegant theories, but never a verified experimental prediction."
This is a totally unfair criticism. If there was experimental evidence against modern theories, then that would be a criticism of them. However, there is currently no experimental evidence either for or against them, since they discuss phenomena that exist at higher energies than we can currently reach in our particle accelerators. Second of all, there is evidence, maybe not direct experimental evidence, but indirect evidence for them, which is that they successfully explain whatever unexplained aspect of the Standard Model or the Universe that they were invented to explain in the first place. Third of all, John Baez and people like him seem to miss the point of what is the purpose of physics. We'll never know the real truth about what is the real Universe at the most fundamental level. All theories in physics are invented by people as attempts to possibly explain unexplained aspects of what we observe, or unexplained aspects of previous theories. We've never had a theory or view of the Universe that was totally true, and we never will. That's not the purpose of physics. The purpose of physics is to explain what you observe. If you think up a theory that has some unexplained aspect or parameter, then you have to try to think up something that could possibly explain it, such as how SU(5) was able to explain the quantization of charge, or predicted the Weinberg angle. By that standard, the extensions of the Standard Model, such as grand unification, supersymmetry, or string theory, are as successful as any theory we've ever had in physics, and there is not a shred of experimental evidence against them. The only thing the critics could point to is the lack of detection of proton decay, which only ruled out the simple SU(5) model all by itself, which no one seriously thought was the ultimate description of nature anyway. Even if these theories turn out not to be true, so what? They explained what they were intended to explain, and were consistent with all experimental data that existed at the time of their invention, which is the most anyone could ask of any theory. We've never had a theory that was actually true, and we never will. For instance, Newtonian mechanics is obviously not true, since it doesn't take into account relativity or quantum mechanics. Is that a valid criticism of Newton?