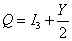
SO(10) is actually a combination of the two simplest extensions of the Standard Model, one being SU(5), and the other being the left-right symmetric model. This model was invented to explain parity violation, which is one of the unexplained aspects of the Standard Model. Weak interactions are parity violating, but this has to be added to the theory in an ad hoc way. The Standard Model does not address the question of why nature is parity violating. The left-right symmetric model explains this by suggesting that the Standard Model is embedded in a higher gauge group that is parity conserving. Then through symmetry breaking, it reduces to the smaller subgroup which survives to low energies, and is parity violating. The left-right symmetric model is perhaps more accurately described as an extension of electroweak theory. At high energies, the gauge group is SU(2)L x SU(2)R x U(1)B - L, and at low energies, it reduces to the SU(2)L x U(1) group of electroweak theory. The SU(3) group of the strong force is carried along unaffected by this symmetry breaking. One interesting thing is that the U(1) group of the Standard Model is now associated with the B - L quantum number, which is baryon number minus lepton number. This model predicts that at high energies, when the symmetry is unbroken, you should see effects associated with parity conservation, such as the right-handed neutrino, right-handed charged currents, and a second neutral Z0 boson. The left-right model allows for a right-handed neutrino, and thus neutrino mass. It makes the weak force more similar to the strong force, so the forces are more consistent, and more unified. It provides a possible interpretation of the U(1) group. It can also provide an alternative explanation for CP-violation, other than the KM-matrix. In the Standard Model, the Gell-Mann-Nishima relation is
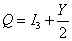
Q = I3 + Y/2
In the left-right symmetric model, this is modified to
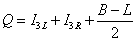
Q = I3L + I3R + (B - L)/2
SO(10) is then a combination of the SU(5) model with the left-right symmetric model, having the benefits of each. Unlike SU(5) which is rank 4, SO(10) is rank 5 with the extra diagonal generator of SO(10) being B - L, as in the left-right symmetric model. The advantage of SO(10) over SU(5) as the group for grand unification is one 16-dimensional spinor representation of SO(10) has all the right quantum numbers to accommodate all the fermions, including the right-handed neutrino, of one generation. The gauge interactions of SO(10) conserve parity, thus making parity a continuous symmetry. Aside from providing a reason of why and how parity is violated in the Standard Model, it helps avoid the cosmological domain wall problem. SO(10) is the minimal left-right symmetric grand unified theory that gauges the B - L symmetry, and is the only simple grand unified group that does not need mirror fermions. The model does not have any global symmetries. Here are the different possible dimensional representations of SO(10), and their decomposition to irreducible multiplets. These are called branching ratios.
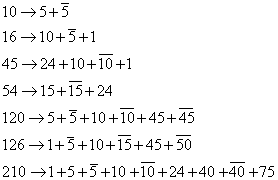
10 -> 5 + [5 bar]
16 -> 10 + [5 bar] + 1
45 -> 24 + 10 + [10 bar] + 1
54 -> 15 + [15 bar] + 24
120 -> 5 + [5 bar] + 10 + [10 bar] + 45 + [45 bar]
126 -> 1 + [5 bar] + 10 + [15 bar] + 45 + [50 bar]
210 -> 1 + 5 + [5 bar] + 10 + [10 bar] + 24 + 40 + [40 bar] + 75
Here are the various ways in which the SO(10) group can break down to the lower subgroups.
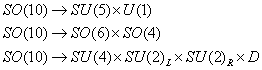
SO(10) -> SU(5) x U(1)
SO(10) -> S0(6) x SO(4)
SO(10) -> SO(4) x SU(2)L x SU(2)R x D
where D is the discrete symmetry of charge conjugation.
qL -> [q bar]L
The following is one way to define the algebra of SO(10). Let's say you have a set of operators Xi ( i = 1, 2…n) and their hermitian conjugate Xi†, satisfying the following anticommutation relation.
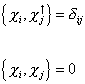
{ Xij, Xj†} = [delta]ij
{Xi, Xj} =0
The operators Tji are defined as
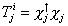
Tji = Xj† Xj
satisfy the algebra of the U(n) group
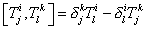
[Tji, Tlk] = [delta]jk Tli - [delta]li Tjk
Let's define the following 2n-operators
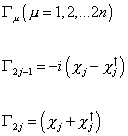
[capital gamma]2j - 1 = -I(Xj - Xj†)
[capital gamma]2j = (Xj + Xj†)
where j = 1, 2,…n
Therefore
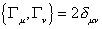
{[capital gamma]u, [capital gamma]v} = 2[delta]uv
Therefore, the Γu's form a Clifford algebra of rank 2. Also
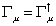
[capital gamma]u = [capital gamma]u†
Therefore, using the Γu's, we can construct the generators of the SO(2n) group as follows
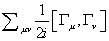
[capital sigma]uv = (1/2i)[[capital gamma]u, [capital gamma]v]
The Σuv can be written down in term of Xj and Xj† as follows.
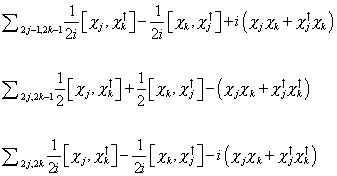
[capital sigma]2j - 1, 2k - 1 = (1/2i) [Xj Xk†] - (1/2i)[Xk, Xj†] + I(XjXk + Xj†Xk)
[capital sigma]2j, 2k - 1 = (1/2) [Xj Xk†] + (1/2)[Xk, Xj†] - (XjXk + Xj†Xk†)
[capital sigma]2j, 2k = (1/2i) [Xj Xk†] - (1/2i)[Xk, Xj†] - I(XjXk + Xj†Xk†)
The spinor representation of SO(2n) is 2n dimensional. Let's define a vacuum state |0> that is SU(n) invariant. The 2n dimensional representation is then given by
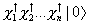
X1† X2† ... Xn† |0>
This representation can be split into the 2n - 1 dimensional representation by using a chiral projection operator. To construct this operator, define
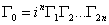
[capital gamma]0 = in [capital gamma]1 [capital gamma]2... [capital gamma]2n
Also define the number operator
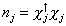
nj = Xj† Xj
Γ0 can be written as
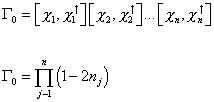
[capital gamma]0 = [X1, X1†] [X2. X2†] …[Xn, Xn†]
[capital gamma]0 = [product of j - 1 to n](1 - 2nj)
Since the number operator satisfies nj2 = nj, you have
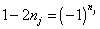
1 - 2nj = (-1)nj
so therefore you have
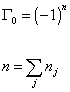
[capital gamma]0 = (-1)n
n = [summation of j] nj
so then you have
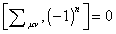
[[capital sigma]uv, (-1)n] = 0
so then the chirality projection operator is given by
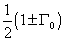
(1/2)(1 ± [capital gamma]0)
Each irreducible chiral subspace is therefore characterized by either an odd or even number of X particles.
We are constructing the spinor representation of SO(2n) that includes SU(n). Since we want specifically to write down the representation of SO(10) that includes SU(5), lets say n = 5. Also, let's define a column vector | Ψ > such that
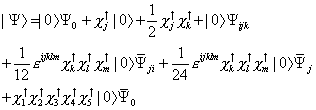
| [psi] > = | 0 > [psi]0 + Xj† | 0 > + (1/2) Xj† Xk† + | 0 > [psi]ijk + (1/12) [epsilon]ijklm Xk† Xl† Xm† | 0 > [psi bar]ji + (1/24) [epsilon]jklmn Xk† Xl† Xm† Xn† | 0 > [psi bar]j + X1† X2† X3† X4† X5† | 0 > [psi bar]0
where [psi bar] is not the complex conjugate of X but rather an independent variable. You can then write
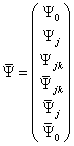
under chirality
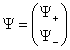
where
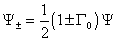
X± = (1/2) (1 ± [capital gamma]0) [psi]
and
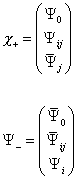
Therefore, for n = 5, [Psi bar]i is the [5 bar]-dimensional representation. Ψij is the 10-dimensional representation, and Ψ0 is a singlet. All the fermions are assigned to Ψ+.
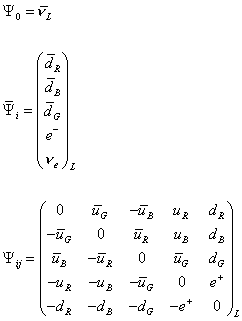
so there are the 16 particle states of SO(10) which are all in the Ψ+ group.
The existence of the right-handed neutrino allows for the neutrinos to acquire mass in a similar way to the other fermions. However, you then have to explain why the neutrino masses are so much smaller than the other fermion masses. A possible explanation suggested by Gell-Mann, Ramond, and Slansky is to use the 126-dimensional representation of SO(10). Their idea was to give a nonzero vacuum expectation value to the SU(5) singlet part of the 126-dimensional representation of SO(10).
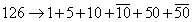
126 -> 1 + 5 + 10 + [10 bar] + 50 + [50 bar]
The Higgs representation that acquires vacuum expectation values in this case is the right-handed triplet, as in the left-right symmetric model. Therefore, the smallness of the neutrino mass is due to the suppression of V + A currents. You know how in the Standard Model, the weak force has a V - A current? This assumes the neutrino is massless. If the neutrino has mass, then there would also be V + A currents. However, if those currents are suppressed, that would explain why the neutrino masses are so small.
For SO(2n), the Higgs field φu is 2n dimensional, and the Higgs field φuvλ has a dimension of
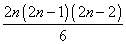
(2n(2n - 1)(2n - 2)/6)
so for n = 5, φu is 10-dimensional, and φuvλ is 120-dimensional. The SU(5) singlet component of φuvλ has the form
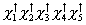
X1† X2† X3† X4† X5†
or
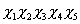
X1 X2 X3 X4 X5
This gives a Majorana mass only to the right-handed neutrino, while the Dirac masses arise from the introduction of the 10-dimensional Higgs. In the left-right symmetric model and SO(10), the neutrino masses are in the following matrix.
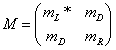
In a Dirac neutrino, mL is equal to mR = 0, and mD is not zero.
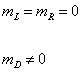
In a Majorana neutrino, either mL or mR, or both are nonzero. mD is arbitrary.
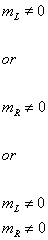
In a Pseudo-Dirac neutrino, mD is not zero. mL is equal to mR, and they are much less than mD
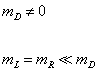
Working with chiral spinors, you choose the appropriate Higgs boson couplings so the mass matrix has the following form
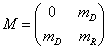
In a more realistic model, minimization of the potential leads to the following modification of the mass matrix
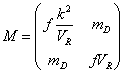
where VR is the right-handed component of the Higgs potential, and k is a constant. This upsets the seesaw mechanism. This problem can be solved by breaking the D-parity present in SO(10), at the GUT scale separately from the SU(2)R symmetry, by introducing a 210-dimensional or 45-dimensional Higgs multiplet. In this case, fk2/VR
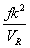
is replaced by fk2VR/MGUT2
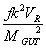
which is tiny if MGUT is large.
Since SO(10) contains the left-right symmetric model, it has an extra neutral Z0 boson called Z'. However, unlike the left-right symmetric model, the constraints of grand unification relate both g1 and g2 at the grand unification scale. Therefore, you have a specific symmetry breaking scheme, and the spectrum of the Higgs boson. All neutral current couplings at low energies are predicted in terms of the SU(2)L gauge group. For SO(10), the neutral current Lagrangian is
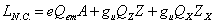
LN. C. = eQem A + guQZZ + gu QX ZX
where in terms of SO(10) generators, you have
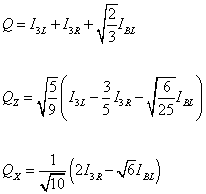
Q = I3L + I3R + [square root of 2/3] IBL
QZ = [square root of 5/9] (I3L = (3/5) I3R - [square root of 6/25] IBL)
QX = 1/[square root of 10] (27 I3R - [square root of 6] IBL)
where A is the photon field, and e = [square root of 3/8]gu.
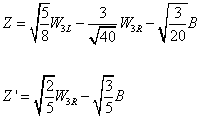
Z = [square root of 5/8] W3L - (3/[square root of 40]) W3R - [square root of 3/20] B
Z' = [square root of 2/5] W3R - [square root of 3/5] B
SU(5) and SO(10) are the two main grand unified theories, although there are others. There are grand unified theories based on the exceptional group E6. There is an unusual grand unified theory called horizontal symmetry that attempts to explain why we have three generations of fermions. The Pati-Salam model is based on the group SU(4) x SU(2) x SU(2). The trinification model is based on the group [SU(3)]3 = SU(3) x SU(3) x SU(3). The 331 model is based on the group SU(3) x SU(3) x U(1).
One of the unanswered questions in physics is why is the Universe overwhelmingly composed of matter instead of antimatter. If there were large amounts of antimatter in the Universe, we would be able to detect a diffuse gamma ray background resulting from matter-antimatter annihilations. However, according to particle physics, particles should not be favored over antiparticles. If the Universe started out with equal amounts of matter and antimatter, it would not be able to get to the current overwhelming preponderance of matter over antimatter. Therefore, we have to explain the current matter-antimatter asymmetry. Since, a proton has a baryon number of 1, and an antiproton has a baryon number of -1, you could call this baryon asymmetry. Why does the Universe have a net positive baryon number?
Andrei Sakharov determined the three conditions, called the Sakharov criteria, that must be met to create the current baryon asymmetry.
1. B violation - Obviously, you need some way of violating baryon number in the first place.
2. C and CP violation - If C or CP are exact symmetries, then the total rate for any process that produces an excess of baryons is equal to the rate of the complementary reverse process that produces an excess of antibaryons, so no net baryon number is created.
3. Departure from thermal equilibrium.
Since grand unified theories, by their very nature, violate baryon number conservation, they are an obvious solution to the baryon asymmetry of the Universe. Unfortunately, even though they violate baryon number, they do not violate B - L. Even SO(10), which has a singlet associated with the antineutrino, which has a lepton number of -1, does not violate B - L. This choice of lepton number assignment does not lead to a new gauge boson that violates B - L. If B - L is conserved, then SO(10) is C symmetric. The generation of baryon asymmetry requires C violation. The C symmetry must be broken before baryon number can be created. However, the C symmetry is not broken until the U(1)B - L symmetry is broken, at which time, it can't violate baryon number, or such processes are very rare. Thus, grand unified theories, in their simple form, can't explain the baryon asymmetry of the Universe. However, if you have an SO(10) model with a heavy Majorana neutrino to explain the smallness the light neutrino masses, then the decay of the right-handed neutrino can break B - L symmetry. This then does allow the possibility that grand unified theory could explain the baryon asymmetry.
To understand grand unification at a deeper level, you have to know more group theory than I've previously described. Unfortunately, this branch of mathematics is a vast and complicated subject, and an in depth comprehensive discussion of it would take us too far away from particle physics. Therefore, I will just briefly describe the main groups within the context of Dynkin diagrams. A Coxeter matrix of rank n is an n x n matrix M with Mii = 1 and Mij = Mji > 1, and possibly infinite, for all i and j in (1, 2, … n). A Coxeter group is a group generated by the elements Pi with i in (1, 2, …n) subject to the relations
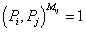
(Pi, Pj)Mij = 1
where Mij are the elements of a Coxeter matrix.
A Coxeter diagram is a diagram used to visualize a Coxeter group. It is a labeled graph with nodes indexed by the generation of a Coxeter group, and (Pi, Pj) is an edge whenever Mij > 2 which is labeled with Mij, where Mij is an entry in the Coxeter matrix corresponding to a given Coxeter group.
You can also talk about this in terms of taking reflections of vectors. Every element of a finite reflection group is a product of reflections through vectors called roots. These roots are all at angles π/n from each other, where n > 1 is an integer. To describe the group, you draw a diagram with one dot for each root. If two roots are perpendicular, you don't draw a line between them. If they are at an angle π/n from each other, you draw one or more lines between them. If n = 3, you just draw one line. If n = 4, you draw two lines. If n = 5, you draw three lines. If n > 5, you draw one line, and label it with the integer n. Usually, the roots are all the same length, but if two roots are connected where one is shorter than the other, the line between them is marked with an arrow pointing to the shorter root. If the roots are the same length, that's called simply laced. Here are the Coxeter diagrams for the finite reflection groups.
1.
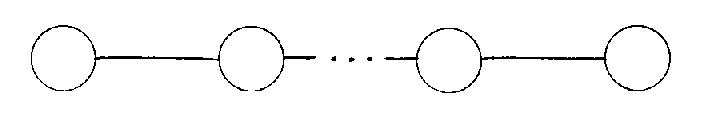
An has a finite number of n dots. A2 is the group of symmetries of an equilateral triangle. A3 is the group of symmetries of a tetrahedron. More generally, An is the group of symmetries of an n-dimensional simplex, which are analogs of the tetrahedron in n dimensions.
The Lie algebra of An is sl{n + 1} (c), the (n + 1) x (n - 1) complex matrices with vanishing trace, which form a Lie algebra. The compact real form of sl{n + 1} (c) is sun, and the corresponding compact Lie group is SU(n), the n x n unitary matrices of determinant 1. The symmetry group of the electroweak is U(1) x SU(2), where U(1) is the 1 x 1 unitary matrix. The symmetry group of the strong force is SU(3). The simplest grand unified theory has the symmetry group SU(5).
2.
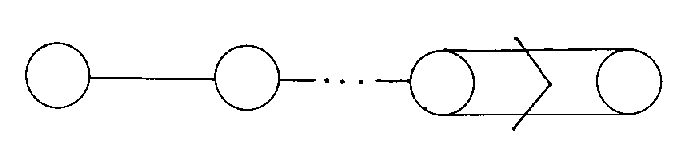
Bn has a finite number of n dots. The angle between the roots is π/4, so one of the edges has n = 4, which is represented by a double line. For Bn, all the roots except the last one are [square root of 2] times as long as the last one. Therefore, the arrow points to the last dot. B2 is the group of symmetries of a square. B3 is the group of symmetries of the cube or octahedron. More generally, Bn is the group of symmetries of an n-dimensional hypercube or hyperoctahedron in n dimensions.
The Lie algebra of Bn is so{2n + 1} (C), the (2n + 1) x (2n + 1) skew-symmetric complex matrices with vanishing trace. The compact real form of SOn (C) is son, and the corresponding compact Lie group is SO(n), the n x n real orthogonal matrices with determinant 1, which is the rotation group in Euclidean n-space. One of the main grand unified theories is based on SO(10). In superstring theory, you see the group SO(32).
3.
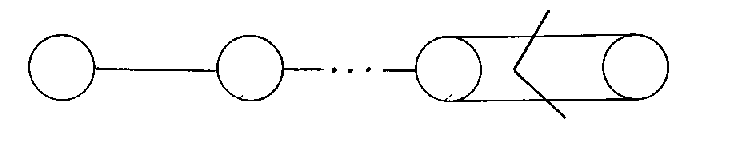
Cn is the same as Bn except that all the roots except the last one are 1/[square root of 2] times as long as the last one. Therefore, the last root is longer than the others, and the arrow points away from the last one to the others. Obviously, if there are just two roots, Bn and Cn are identical, and so to avoid redundancy, we say that for Cn, n > 2. Bn and Cn are duals to each other. Cn is also the group of symmetries of a hypercube or hyperoctahedron in n dimensions.
The Lie algebra for Cn is spn (C), the 2n x 2n complex matrices of the form
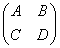
where B and C are symmetric, and D is minus the transpose of A. The compact real form of spn is spn, and the corresponding Lie group is called Sp(n). This is the group of n x n quaternionic matrices which preserve the usual inner product on the space Hn of the n-tuples of quaternions.
4.
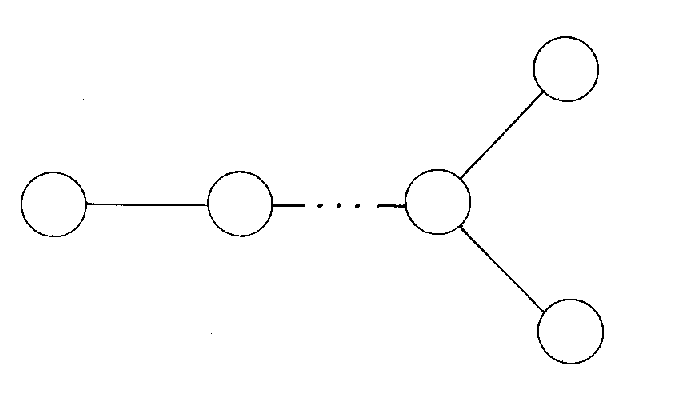
The Lie algebra of Dn is so{2n} (C), the 2n x 2n skew-symmetric complex matrices with vanishing trace.
In unfortunate conflicting notation, sometimes you see Dn used to refer to the dihedral group which we're calling Im.
5.
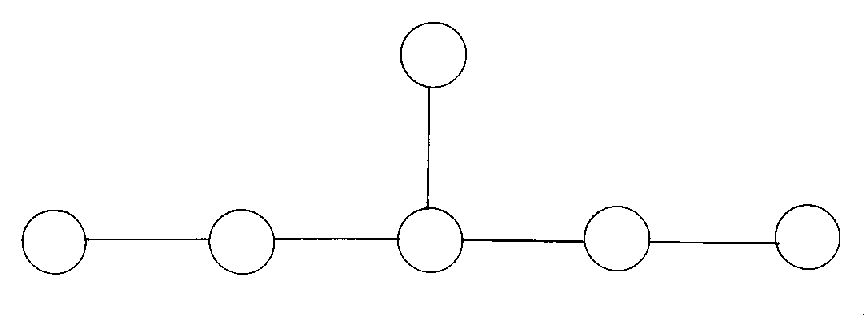
E6 is a 78-dimensional Lie algebra. It's smallest representation is 27-dimensional, consisting of all the 3 x 3 hermitian matrices over the octonions, on which it preserves the commutator. E6 is used in grand unified theories. The E6 group is important in the symmetry breaking of Heterotic E8 x E8 superstring theory.
6.
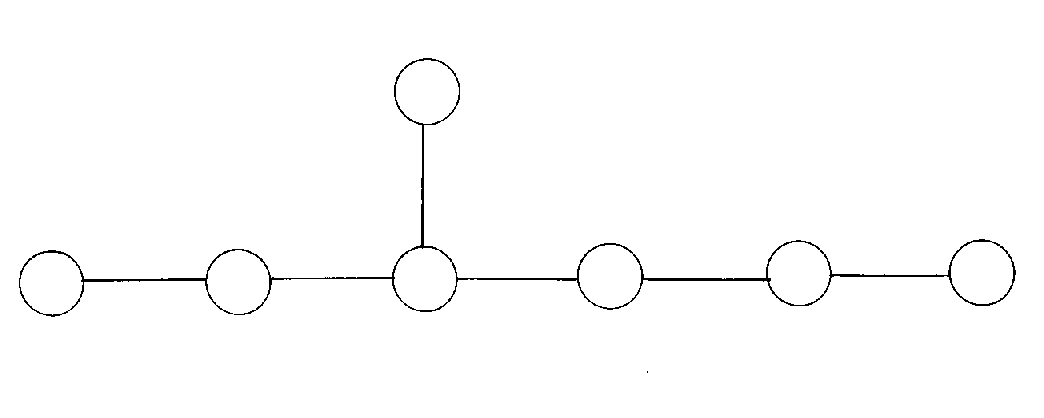
E7 is a 133-dimensional Lie algebra. It's smallest representation is 56-dimensional, on which it preserves a tetralinear form.
7.
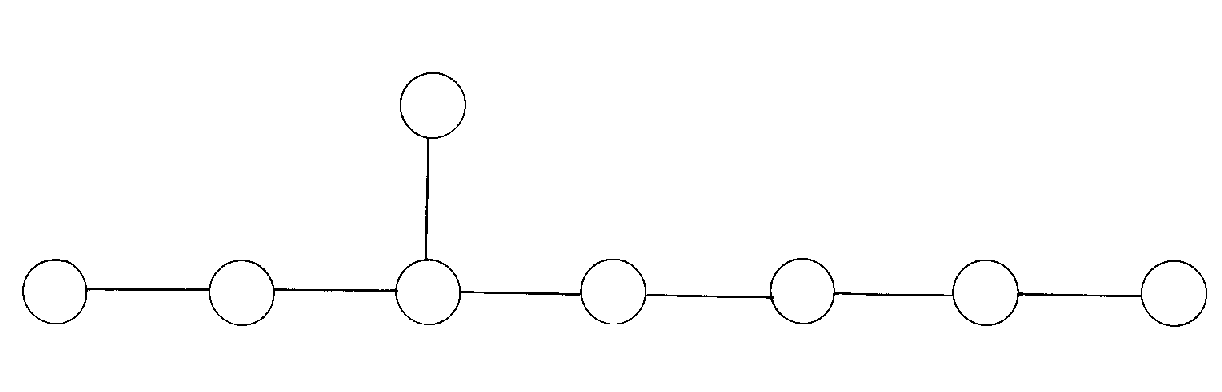
E8 is a 248-dimensional Lie algebra, the biggest of the exceptional Lie algebras. It's smallest representation is 248-dimensional, the adjoint representation in which it acts on itself. The easiest way to understand the Lie group E8 is as the symmetries of itself. You can get its root lattice, the 8-dimensional lattice spanned by its roots, by using the icosahedron and quaternions. The E8 group is used in superstring theory. Specifically, it appears in Heterotic E8 x E8 superstring theory.
8.
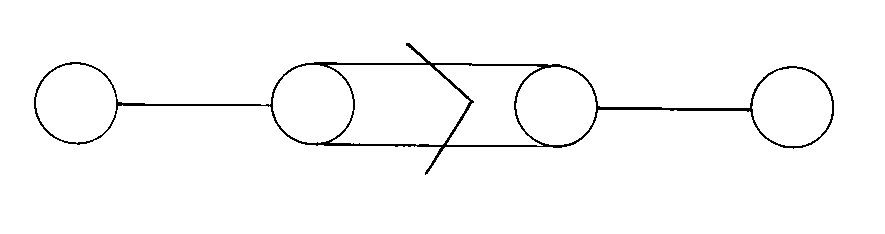
F4 is a 52-dimensional Lie algebra. It's smallest representation is 26-dimensional, consisting of traceless 3 x 3 hermitian matrices over the octonions, on which it preserves a trilinear form. F4 is the group of symmetries of a four-dimensional polyhedron, or polytope, called the 24-cell. A four-dimensional polytope is called a polychoron.
9.
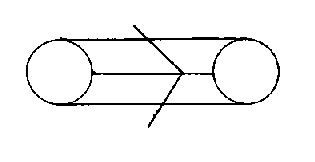
G2 is a 14-dimensional Lie algebra, and the compact Lie group corresponding to its compact real form is also called G2. This group is the group of symmetries, or automorphisms, of the octonions. The smallest representation of this Lie algebra is 7-dimensional, corresponding to the purely imaginary octonions. The G2 group is relevant to the type of manifold that is used to compactify the extra dimensions in M-theory.
10.
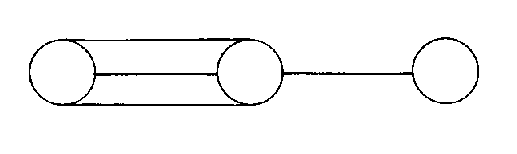
H3 is the group of symmetries of the dodecahedron and icosahedron. There is no associated Lie algebra.
11.

H4 is the group of symmetries of a four dimensional polyhedron, or polytope, called the unit icosian or 120-cell, which has 120 vertices, and is closely related to the dodecahedron and iscosahedron. There is no associated Lie algebra. The fact that the H groups stop at four is the reason why there are no analogs of the dodecahedron or icosahedron in more than four spatial dimensions.
12.
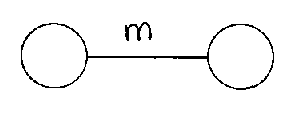
Im corresponds to the symmetry group of the 2m-gon, or polygon with 2m sides, in a plane. There is no associated Lie algebra.
A lattice is formed by taking n linearly independent vectors in n-dimensional Euclidean space, and forming all possible linear combinations with integer coefficients. Whether or not there exists a lattice for a given symmetry group is called the crystallographic condition. If a symmetry group satisfies the crystallographic condition, then there exists a symmetry group with that symmetry. In the above list, the ones that satisfy the crystallographic condition are
An, Bn, Cn, Dn, E6, E7, E8, F4, and G2
These are the symmetry groups corresponding to the semisimple Lie algebras of the same name. Their Coxeter diagrams are called Dynkin diagrams. There are four infinite groups, called the classical series, and five others, called the exceptional groups. The fact that the H groups do not satisfy the crystallographic condition is the reason why there are no naturally occurring crystals with dodecahedral or icosahedral symmetry, although in 1982, Dan Shechtman discovered quasicrystals, which can have dodecahedral or icosahedral symmetry. Dan Shechtman received the 2011 Nobel Prize in Chemistry for the discovery of quasicrystals.
If you take a d-dimensional polytope, such as a regular polygon or polyhedron, and you exchange the (d - 1)-dimensional components with vertices, and vice versa, you get a dual to the original polytope. For example, the dual of the cube is the octahedron. If the polytope is associated with a Dynkin diagram that has left-right symmetry, then the polytope is self-dual.
The infinite series of simple Lie groups associated to rotations in real vector spaces which are the SO(n) groups, are the B and D series. The infinite series of simple Lie groups associated to rotations in complex vector spaces is the SU(n) groups, which is the A series. The infinite series of simple Lie groups associated to rotations in quaternionic vector spaces is the Sp(n) groups, which is the C series. The five exceptional groups are related to the octonions.