Cosmology is the study of the entire Universe on the grand scale. Therefore, the two most important subjects in existence are cosmology and particle physics, since they attempt to explain the Universe on the grand scale and the most fundamental scale. These two fields are intimately connected. Even though cosmology is one the most important human endeavors, many physicists feel that it has only recently become a serious science in the sense of being testable. Some cosmologists have heralded a new golden area of precision cosmology. We have recently obtained a wealth of new cosmological data from probes and other experiments designed to measure anisotropies of the cosmic microwave background or CMB, especially from the Wilkinson Microwave Anisotropy Probe, or WMAP. We can now say with certainly that the Big Bang occurred 13.7 ± 0.2 billion years ago, and the cosmic microwave background is a snapshot of the Universe 379 ± 8 thousand years later, when atomic nuclei and electrons first combined into atoms, thus becoming transparent to photons. We also have important recent data measuring the redshifts of distant Type Ia supernovae, which establish that the Universe is about 70% dark energy, and 30% matter, 98% of which is dark matter. In other words, ΩΛ = 0.7, Ωm = 0.3, and ΩΛ + Ωm = 1, giving a spatially flat universe. The current cosmological data from a wide variety of sources, such as WMAP, other CMB observations, Type Ia supernovae redshifts, the Lyman alpha forest, primordial deuterium abundances, and gravitational lensing are all consistent with each other as well as being consistent with the theoretical predictions of inflationary cosmology, which has been the predominate theory of cosmology since 1981. This is a great vindication to cosmology, not to mention a relief to cosmologists. In this paper, I use "Universe" with a capital U to mean the real Universe, and "universe" with a lower case u to mean a model universe. It would help if you have read my previous papers on Tensors, Lagrangians, The Standard Model, and Beyond The Standard Model.
The most primitive humans, which were nomadic tribes of hunter-gatherers, assumed the Universe was what they could personally see, which was the land stretching out to the horizon, forming a flat circular disk, with the sky above, forming a hemispherical dome. However, thousands of years ago, they had reason to think the Earth is round because when you see a ship go over the horizon, its sails are the last to disappear, and if you're on a ship looking back at the land, the mountains disappear last. In the 6th Century B.C., the Pythagoreans, followers of Pythagoras of Samos (569 B.C. - 475 B.C.), claimed not just that the Earth was spherical, but that the Earth revolved around the Sun, or actually a "central fire" different from the Sun. Eudoxus of Cnidus (410 B.C. - 355 B.C.) attempted to explain the motion of the planets by using 27 spheres, and Callipus (370 B.C. - 300 B.C.) claimed that 34 spheres were needed. Aristarchus of Samos (310 B.C. - 230 B.C.) was an advocate of heliocentric motion. However, this view was a minority view, and most scientists believed in the geocentric system, such as that proposed by Claudius Ptolemy (85 A.D. - 165 A.D.). In order to explain the motions of the planets, they were assumed to periodically loop back upon themselves in epicycles. Archytas of Tarentum (428 B.C. - 350 B.C.) came up with an argument as to why the Universe was infinite, although most people assumed the Universe was finite, and was contained within the celestial sphere on which the stars were printed. The Ptolemaic system remained unchallenged until Nicholas Copernicus (1473 - 1543) in the 16th Century. Copernicus' system did not match the accuracy of Ptolemy's geocentric system. The reason was that Copernicus still assumed that the planets moved in circular orbits. This problem was solved when Johannes Kepler (1571 - 1630) proposed that they moved in elliptical orbits. Kepler proposed Kepler's Laws. Kepler's employer Tycho Brahe (1546 - 1601), who had a gold nose, advocated a system where the Sun and Moon orbit the Earth but the other planets orbit the Sun. Tycho also saw a supernova suggesting the heavens aren't unchanging. When Galileo Galilei (1564 - 1642) turned the telescope to the sky, it revolutionized astronomy. He discovered moons of Jupiter, proving that not everything orbited the Earth. Due to Galileo, heliocentric motion became the majority view, yet even with the telescope, the stars looked the same, tiny pin pricks, of light, and he couldn't detect any parallax, suggesting they were farther away than anyone imagined. Up until that point, it was assumed that the Solar System was the Universe. Then in the 1570's, there was a shift, and it came to be believed that there was no celestial sphere, and the stars were scattered throughout space, which was the theory proposed by English astronomer Thomas Diggs in 1576. Isaac Newton (1643 - 1727) revolutionized physics with Newtonian mechanics which unified terrestrial and celestial mechanics. Pierre-Simon Laplace (1749 - 1827) mathematically explained all the dynamics of the Solar System. In 1823, Heinrich Olbers (1758 - 1840) put forward Olber's paradox, which had been suggested by numerous people beforehand including Johannes Kepler, Edmund Halley, and Jean-Phillipe de Cheseaux, which was that there is an apparent paradox with an infinite universe, which is that we should see stars everywhere in the sky, but this was on the assumption that the Universe had existed for an infinite length of time. The first stellar parallax, which was of the star 61 Cygni, was measured in 1838 by Friedrich Wilhelm Bessel (1784 - 1846), who is better known for the Bessel functions. The nearest star turned out to be 25 trillion miles away. Parallax is like if you extend your arm, and stick out your thumb, and close one eye, and then close only the other eye, its apparent position against the background changes.
Since ancient times, it was recognized that most stars are in a bright band across the sky called the Milky Way, thought to resemble milk from the breast of the Greek goddess Hera. By the turn of the century, the Milky Way was recognized to be a giant disk shaped structure that contains most stars. However, most astronomers in the early 20th Century assumed that the Milky Way Galaxy was the Universe. Just as before, it was assumed that the Solar System was the Universe, it was now assumed that the Milky Way Galaxy was the Universe. There were a minority of people who disagreed with this. In 1755, philosopher Immanuel Kant (1724 - 1804) theorized that some of the nebula which astronomers saw might actually be galaxies like the Milky Way, very far away. Kant referred to them as "island universes". In 1918, Shapley studied Cepheids, which are bright stars which pulsate at regular intervals from a few days to a month. Using Cepheid variables, he established that some of the nebula were very far away, proving the other galaxies theory. Starting in 1912, Vesto Slipher (1875 - 1969) measured spectra from the nebula, many of which are really galaxies, showing that many appeared to be Doppler-shifted. The Doppler effect is like when the pitch of the sound of a train seems to change as it goes pass you, although that’s not actually what's happening with the galaxies. By 1924, Slipher had measured 41 nebulas, and 36 were red-shifted, meaning they were receding from us. This was made more rigorous by Edwin Hubble (1889 - 1953) in 1923 - 1929. Hubble was able to resolve Cepheids in the Andromeda galaxy using the 100-inch telescope on Mount Wilson. He developed a new distance measure using the brightest star for more distant galaxies. He correlated these measurements with Slipher's nebula, and discovered Hubble's Law, v = Hd, where v is the velocity, d is the distance, and H is Hubble's constant, which he overestimated.
If all the galaxies were redshifted, that means they are all running away from each other, which means if you extrapolate backwards, the Universe must have had a beginning. Einstein would have been considered an even bigger genius than he was if he had predicted this ahead of time, which he could have since that's what his own theory of general relativity suggested. You can't really blame him for that since you think up theories to explain what you observe, and he thought up general relativity in 1915, and proposed a cosmological model in 1917, before there was much evidence that the Universe was expanding. Einstein inserted a term called the cosmological constant into his theory in order to allow for a static universe, which he later called the greatest blunder of his life. In 1917, Russian cosmologist Alexander Friedman (1888 - 1925) recognized that Einstein's theory of general relativity allowed for an expanding universe. Einstein's static universe was unstable. In 1917, Dutch astronomer William de Sitter (1872 - 1934) invented another static universe that turned out to be unstable, and then a universe that expands indefinitely was called a de Sitter universe. Model universes were studied by Russian cosmologist Alexander Friedman (1888 - 1925) in 1922 and 1924, and independently by Belgian priest Georges Lamaitre (1894 - 1966) in 1927. In 1930, Eddington proved that Einstein's model was unstable, and proposed a non-static model. In 1933, A. G. Walker and H. P. Robertson independently proved that what we now call the Robertson-Lamaitre metric is the only one consistent with a homogenous isotropic universe. Despite the redshift data, many people denied that the Universe had a beginning. Fred Hoyle invented the name "Big Bang" as a derogatory insult of the theory that the Universe had a beginning, and the name stuck. Many people, including Fred Hoyle, Herman Bondi, and Thomas Gold, advocated the Steady State model, that the Universe had existed forever, and that new matter was constantly being created from nothing to fill in the gaps.
The great debate between the Big Bang theory and the Steady State theory was finally put to rest in favor of the Big Bang in 1964 when Arno Penzias and Robert Wilson discovered the cosmic microwave background radiation. Working with a 7.35 cm horn antenna at Bell Labs, Penzias and Wilson accidentally discovered an isotropic radio background. This cosmic microwave background was very strong evidence in favor of the Big Bang model, and it convinced most people. The temperature of this black body radiation is 2.725 K. This cosmic microwave background had actually been predicted by George Gamow in 1948, and by Ralph Alpher, and Robert Herman in 1949. Gamow had other advocates of the Big Bang had thought that all the elements had been created in the Big Bang. It turned out that only hydrogen and helium were produced in the Big Bang, and the other elements were created in stars. However, the relative abundances of the elements hydrogen and helium predicted by the Big Bang theory were in good agreement with observations. Despite these successes, there were problems with the Big Bang model, which were the horizon problem, the flatness problem, and the monopole problem. However, these problems are solved if you postulate an interval of enormous inflation in the very beginning of the Universe. This is called inflationary cosmology, and was originally invented by Starobinsky, and later developed by Alan Guth and Andrei Linde in 1981. Ironically, inflation, which saved the Big Bang model, raised the possibility of eternal inflation, which means the Universe could have existed for an infinite length of time after all. Also, in the 1970s, Rubin, Freeman, and Peebles measured the rotation curves of spiral galaxies, and found they did not obey Kepler's Laws, specifically the velocity did not drop off with distance, which suggested the existence of dark matter. In 1986, de Lapparent, Geller, and Huchra did deep redshift galaxy surveys that demonstrated the existence of large scale structure in the form of huge bubbles, filaments, and sheets on scales from 25 megaparsecs to 100 megaparsecs. One parsec equals 3.09 x 1016 meters, or 3.26 light-years. In April 1992, the COBE satellite team announced the discovery of anisotropies in the cosmic microwave background at the level of one part in 100,000, proving how isotropic the Universe is. In 1995-1996, the Hubble telescope was able to resolve Cepheid variable stars in galaxies in the Virgo cluster, giving a much better calibration of the distance measures, and therefore a more accurate estimate of Hubble's constant. In 1998, a balloon-based experiment called Boomerang in Antarctica measured the anisotropy of the cosmic microwave background. Also, in 1998, two separate teams, one led by Saul Perlmutter, and the other led by Brian Schmidt, announced their results from studying the redshifts from Type Ia supernovae, and determined that the expansion of the Universe is accelerating, so we do have some sort of effective cosmological constant after all. In June 2001, the WMAP probe was launched, and the results were published in February 2003, providing overwhelming confirmation of inflationary cosmology.
The general trend in the history of cosmology has been towards recognizing our own insignificance, for instance, that the Sun and other planets do not revolve around the Earth, our solar system is not the Universe, our galaxy is not the Universe, we are located on the edge of a typical galaxy that is only one of 100 billion galaxies in the observable universe, and baryonic matter, such as makes up us, constitutes only about two percent of all matter. This is called the Copernican principle, which states that we are typical observers, and there is nothing special about us. Rather than be disappointed by this blow to our ego, we should appreciate this fact which makes cosmology possible. If we are typical observers, we can be rest assured that our local region of space is representative of the Universe, and that observers anywhere in the Universe would see basically the same thing we see. Without that assumption, it would not be possible to do cosmology at all. However, there is also another principle called the anthropic principle that states that only certain parts of the Universe are likely to produce life, and so the mere fact we are here shows we are not in a completely typical part of the Universe. For instance, a point in the Universe chosen at random would be very unlikely to be as close to a star as we are. Of course, life could only arise near a star, which explains why we are close to a star.
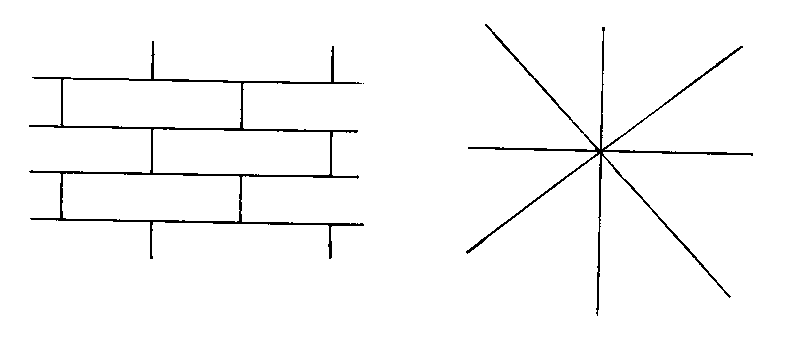
The Copernican principle is related to two other concepts called homogeneity and isotropy. When Friedman, Robertson, and Walker tried to mathematically model the universe, they assumed it was homogeneous and isotropic because that was the simplest model, although they didn’t have evidence that it really was homogeneous and isotropic. Today, we know the Universe really is homogeneous and isotropic. Homogeneous means the universe is pretty much the same everywhere. Isotropic means that the universe looks the same no matter what direction you look. The diagram on the left is homogenous, and the diagram on the right is isotropic.

Another way of saying this is that homogeneous means it's invariant under translations, and isotropic means it's invariant under rotations. As another example, an infinite cylinder is homogenous but not isotropic. A cone is isotropic about the vertex but is not homogeneous.
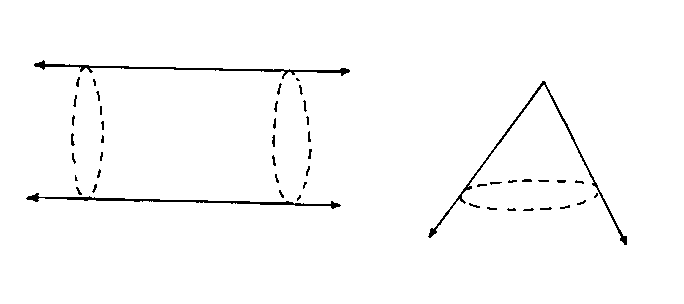
However, if the universe is isotropic about a single point, which it is for us, and you combine that with the Copernican principle, that requires the universe also be homogeneous. The Copernican principle states that if the universe is isotropic about one point, it is therefore isotropic about all points, and is therefore homogeneous. Imagine two intersecting circles.
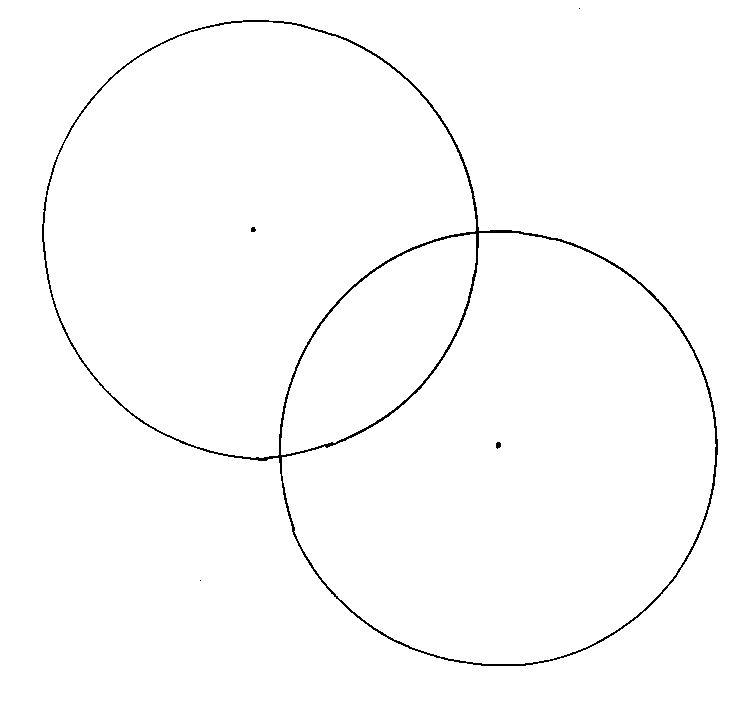
If the observer centered on one circle sees the same thing along the edge of his circle, then an observer centered on the other circle would see the same thing along the edge of his circle. The circles can be made of any size, so any observer would see the same thing everywhere, so the universe would be homogeneous. Therefore, isotropy plus the Copernican principle requires homogeneity. The reverse is not true. Homogeneity plus the Copernican principle does not require isotropy. However, we observe isotropy, and assume the Copernican principle, so we assume the Universe is both homogeneous and isotropic. The isotropy of the Universe is most obvious in the 2.725 K cosmic microwave background which is isotropic to one part in 105.
In ancient Mesopotamia and Egypt, they had what we now call the Pythagorean theorem. The Egyptians used it to redraw the boundaries between farms after the annual flooding of the Nile. Pythagoras was one of the first ancient Greek scientists, although his followers formed a cult devoted to numerology. In the 6th century B.C., Pythagoras traveled to Egypt, learned of the Pythagorean theorem, and brought it back to Greece, where it was named after him. Today, it's the mathematical concept named after the person who lived the longest length of time ago, and he didn't even invent it. In the 19th Century, British schoolboys had to memorize the little ditty, "The area of the square on the hypotenuse is equal to the sum of areas of the squares on the other two sides." This was also recited, inaccurately, by the Scarecrow in "The Wizard of Oz". The quote from the Scarecrow was also repeated by Homer Simpson on "The Simpsons". Let's say you have two points on a Cartesian plane.
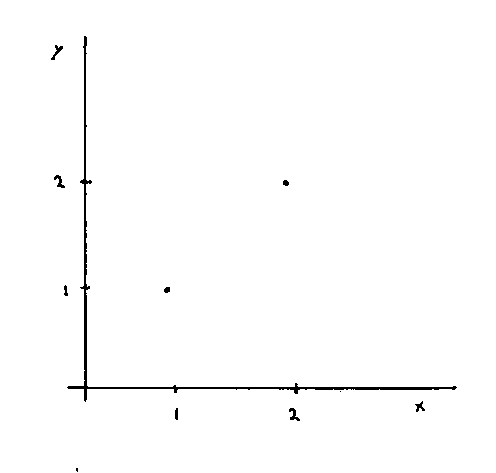
How would you find the distance between them? To find the distance between them, you subtract the x-coordinates and square the result, subtract the y-coordinates and square the result, add the results, and take the squareroot of that.
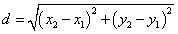
d = [squareroot of][(x2 - x1)2 + (y2 - y1)2]
If you change the coordinate system, the calculated value for the distance between the points is the same.
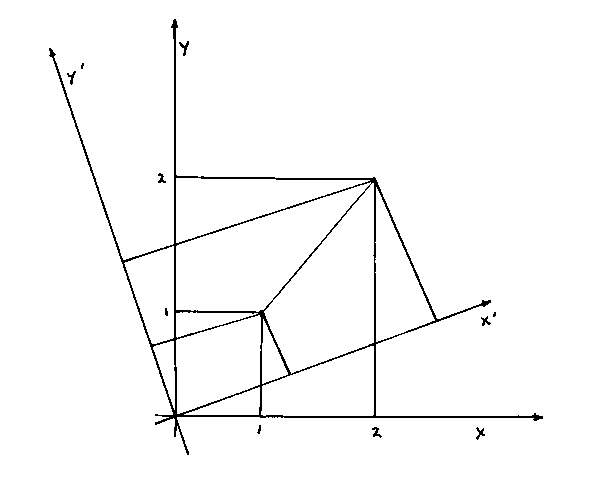
This means that the calculated distance between two points in invariant under a change of axes, which is exactly what you want in physics, since you don't want the measured value of quantities to depend on your coordinate system. You see this concept of invariance throughout physics. You can rewrite the equation
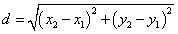
d = [squareroot of][(x2 - x1)2 + (y2 - y1)2]
as
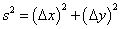
s2 = (Δx)2 + (Δy)2
which is the same under a change in axis.
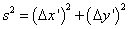
s2 = (Δx')2 + (Δy')2
You can also generalize it to three dimensions.
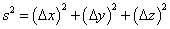
s2 = (Δx)2 + (Δy)2 + (Δz)2
Now let's look at spacetime according to classical Newtonian mechanics. Let's say you have one time dimension, t, and two spatial dimensions, x and y.
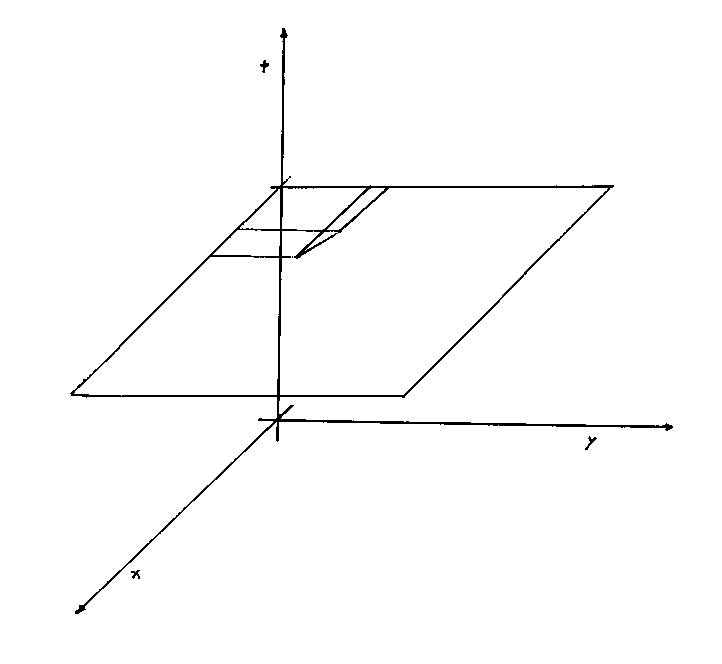
Now, in this system, you have an infinite number of horizontal x-y planes. Within each x-y plane, you can use the Pythagorean theorem to calculate the distance between two points, and the value is the same if you change the x and y axes, such as by rotating them around the t axis. So with an x-y plane at a given t coordinate, you can use the following formula
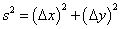
s2 = (Δx)2 + (Δy)2
However, the formula does not work for points that are not at the same t coordinate. In Newtonian mechanics, there is no way to calculate the distance between two points at different t coordinates.
You need some way of generalizing the Pythagorean theorem to allow for measuring the distance between two points with different t coordinates. Now in an x-y-z coordinate system, you would write
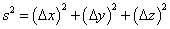
s2 = (Δx)2 + (Δy)2 + (Δz)2
but you can't do that on an x-y-t system because time obviously acts differently than the other dimensions. You need a way to convert between spatial dimensions and the time dimension. The conversion factor is the speed of light, where c = 2.99792458 x 108 m/s. The correct formula for measuring the distance between points in the x-y-t system is
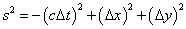
s2 = -(cΔt)2 + (Δx)2 + (Δy)2
or in three spatial dimensions
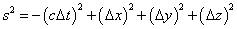
s2 = -(cΔt)2 + (Δx)2 + (Δy)2 + (Δz)2
This is the coordinate system of special relativity. An event is specified by the coordinates (t, x, y, z), and the above defines the spacetime interval between two events. It can be positive, negative, or zero for non-identical points. The interval is unchanged by a change in coordinate system.
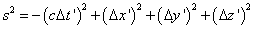
s2 = -(cΔt')2 + (Δx')2 + (Δy')2 + (Δz')2
This is called Lorentzian coordinates, whereas the x-y-z system is called Euclidean coordinates.
The coordinate transformations rotate space and time into each other. There is no fundamental concept of simultaneous events, since whether two events have the same t coordinate depends on the coordinate system used. So, here you have
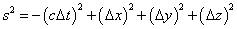
s2 = -(cΔt)2 + (Δx)2 + (Δy)2 + (Δz)2
In order to simplify the notation, we frequently use naturalized units were c = 1, so then
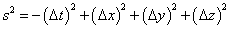
s2 = -(Δt)2 + (Δx)2 + (Δy)2 + (Δz)2
Notice that if you replace t with t times i, you have (it)2 and i2 = -1, which cancels the minus sign in front of t, which turns the Lorentzian coordinates into Euclidean coordinates. This is called a Wick rotation.
In order to write the spacetime interval in more compact form, we introduce the following metric.
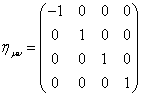
where sometimes it's written with an opposite sign convention. So then, you have
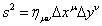
s2 = nuv ΔxuΔyv
Before, in the Euclidean system, the distance between two points was the same if you did a translation or rotation of the axes. What kind of transformations leave the above spacetime interval unchanged? They include translations, rotations, and also boosts, which is going from a motionless frame of reference to one moving at a constant velocity. Boosts and rotations are called Lorentz transformations. Boosts, rotations, and translations are called Poincare transformations.
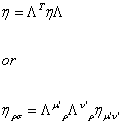
η = ΛT η Λ
or
ηρ σ = Λμ’ρ Λν’σ ημ’ ν’
such that the components of the matrix ημ’ ν’ are the same as those at ηρ σ, so the interval is invariant under those transformations.
The Lorentz transformations form a group under matrix multiplication called the Lorentz group. There is an analogy between the Lorentz group and O(3), the rotation group in 3D space. The rotation group is a set of 3 x 3 matrices R that satisfy
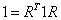
1 = RT1R
The following is an example of a rotation.
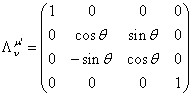
The rotation angle θ is a periodic variable with period 2π. The following is an example of a boost.
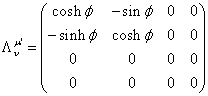
where the boost parameter φ goes from -∞ to ∞.
The boosts correspond to changing coordinates by changing to a frame that is moving at constant velocity with respect to the first frame. The transformed coordinates are given by
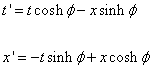
t' = t cosh φ - x sinh φ
x' = -t sinh φ + x cosh φ
If the point defined by x’ = 0 is moving, its velocity is given by
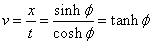
v = x/t = sinh φ/cosh φ = tanh φ
If you replace

φ = tanh-1 v
you get
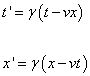
t' = γ (t - vx)
x' = γ (x - vt)
where
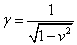
γ = 1/([squareroot of [ 1 - v2)]]
If you don't use naturalized units where c = 1, then
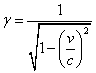
γ = 1/[squareroot of [1 - (v/c)2)]]
Let's look at a boost in the x-t plane.
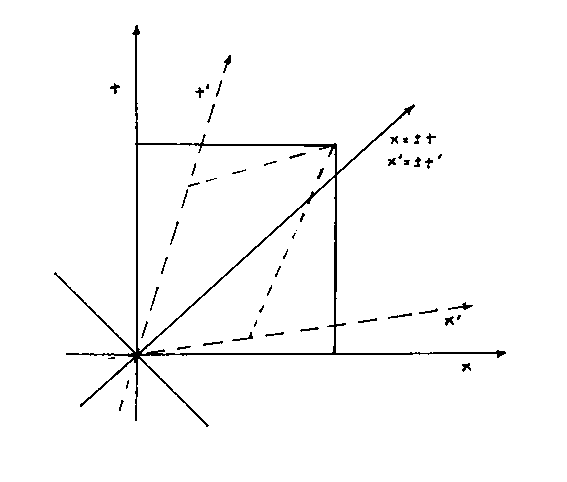
The spacetime axes are rotated into each other, although they do no remain orthogonal. Notice that the path traveled by the light is exactly the same in the new coordinate system as the old one, showing light travels at the same speed for all observers.
Einstein first presented special relativity in 1905. Then in 1908, Russian mathematician H. Minkowski presented a paper called "Space and Time" in which he introduced the Minkowski diagram. Let's say you have one dimension of time, and one dimension of space.
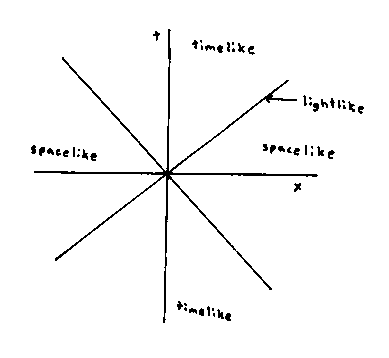
In units where c = 1, the path traced by light passing through the origin would be two lines at right angles to each other, and at 45° angles to the x and t axes. These two lines are called the light-cone, since they would form two cones in an x-y-t system. Points on the lines are called light-like or null. Points above and below the two lines are called time-like. Points to the right and left of the two lines are called space-like. Using the area outside the light-cone as a coordinate frame is called Rindler space.
The spacetime interval is given by
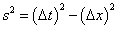
S2 = (Δt)2 - (Δx)2
And so the interval is zero for
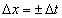
Δx = ± Δt which will only be true if a light-ray can connect the two events since light travels at the speed of one unit of space per one unit of time. Since the interval between points on the light-cone is zero, they are called null.
If the separation between two events A and B is time-like, you can ask if B lies in A's past or future. The top light cone is A's future, and the bottom light-cone is A's past. If the separation between A and B is space-like, you can't assign an absolute order in time to the events A and B. If two events have space-like separation, some people will say A happens first, some people will say B happens first, and some people will say they are simultaneous. If A and B are time-like separated, then everyone will agree.
The set of points for which the spacetime interval is one would be the unit hyperbola.
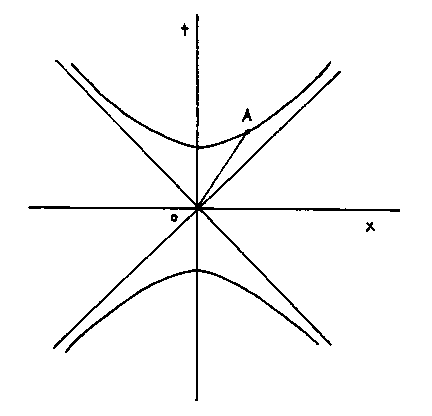
The interval from the origin to A is
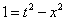
1 = t2 - x2
You can see that for large values, | t | and | x | are approximately equal and thus the graph is asymptotic to the x = ± t lines.
From the point of view of someone traveling from the origin to A, the 0A line is their t axis. If A has coordinates (x', t') in his coordinate system, then x' = 0. Since the interval 0A is one for every observer
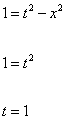
1 = t2 - x2
1 = t2
1 = t
so from his subjective point of view, t would appear to take him one time unit to get to any point on the unit hyperbola.
Ironically, some of the assumptions of special relativity are not true in the real Universe. In special relativity, there is no preferred reference frame, but in the real Universe, you could use the cosmic microwave background as a universal reference frame. In special relativity, there is no cosmic time, but in the real Universe, all observers can start their clocks with the Big Bang.