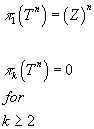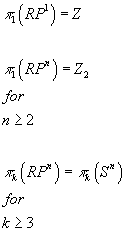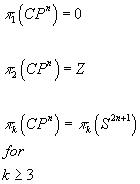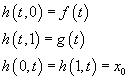
The purpose of this paper is to explain how K-theory is used to classify the allowed Ramond-Ramond field strengths and charges of stable D-branes. In other words, the ultimate goal is to increase our understanding of superstring theory. However, before we can get there, I have to first explain what cohomology is, which means we have to first thoroughly explore the subject of algebraic topology. Fortunately, this is a very interesting subject in its own right. I assume you have read my previous papers Tensors, Lagrangian, The Standard Model, and Beyond the Standard Model. You may remember in my earlier paper "Beyond the Standard Model", at the beginning of the section on string theory, I briefly introduce the subject of topology. Perhaps you would like to reread that section to refresh your memory. In geometry, a triangle is still considered the same shape if you perform the operations of translation, rotation, or reflection, but not if you do a deformation where you change the angles, the lengths of the sides, or add an additional side, and turn it into a square. In topology, you expand what you can do to a shape, and still have it be considered the same shape, to include the deformations that I listed. In other words, unlike in geometry, in topology, a triangle and square are considered the same shape, which for convenience, we call a "circle" and represent by S1. So you see, we're including more operations that leave it invariant then you are familiar with from geometry. In geometry, a tetrahedron and cube would be considered different shapes, but in topology, they are considered the same shape, since one can be easily deformed into the other, and we refer to that shape as a "sphere", represented by S2.
The deformations that you are allowed to do in topology, and have it still be considered the same shape are called homeomorphisms. Two spaces with a homeomorphism between them are called homeomorphic. From the point of view of topology, they are the same shape. A homeomorphism maps points in the first object that are close together to points in the second object that are close together, and of course, points that are far apart are mapped to points in the second object that are far apart. A function f between two topological spaces X and Y is called a homeomorphism if it has the following properties.
1. f is a bijection
2. f is continuous
3. the inverse function f-1 is continuous
If such a function exists, X and Y are homeomorphic. The homeomorphisms form an equivalence relation on the class of all topological spaces. The resulting classes are called homeomorphism classes.
There's an old joke that if a topologist was on his coffee break, he wouldn't be able to tell the difference between his coffee mug and his doughnut, since from the point of view of topology, they are the same shape. The topologist might accidentally take a bite out of his coffee mug like the Mad Hatter in "Alice in Wonderland". Lewis Carroll was a mathematician, but I doubt he thought of that. On the other hand, maybe he did think of it. On the other hand, maybe he did think of it.
You saw that by expanding the operations that leave a shape invariant, you go from geometry to topology. If you expand the operations that leave a shape invariant even further, you go from topology to homotopy. In topology, a disk, D2, which a circle plus its interior, is the same shape as a square plus its interior. However, in topology, a disk would not be the same as a single point. Unlike in topology, in homotopy, a disk would be considered the same as a single point, because homotopy allows you to shrink it all the way down to a single point. A circle, S1, is homotopy equivalent to a punctured plane, which is a plane with one point removed, R2 - {(0, 0)}. You could imagine taking the empty point in the plane, and expanding it to the interior edge of the circle, and then taking the "edge" of the plane, located at infinity, and dragging it in from infinity to the outer edge of the circle. So you see how in homotopy, you have invariance under operations that you do not have invariance under in topology. Every homeomorphism is a homotopy equivalence but the reverse is not true. A disk is homotopy equivalent to a point, but is not homeomorphic to a single point. A space that is homotopy equivalent to a single point is called contractible. A circle and disk are not homotopy equivalent, and thus obviously not homeomorphic either.
The technical definition of homotopy involves the deformation of functions. A homotopy between two continuous functions f and g from a topological space X to a topological space Y is defined to be a continuous function H : X x [0, 1] → Y from the product of space X with the unit interval [0, 1] to Y such that for all points x in X, H(x, 0) = f(x) and H(x, 1) = g(x). Therefore, H describes a continuous deformation of f into g. At time 0, you have function f, and at time 1, you have function g. Being homotopic is an equivalence relation on the set of all continuous functions from X to Y. If f1g1 : X → Y are homotopic, and f2g2 : Y → Z are homotopic, then their compositions f2 * f1 and g2 * g1 : X → Z are also homotopic.
If you have two spaces X and Y, they are homotopy equivalent, or of the same homotopy type, if there exists continuous maps f : X → Y and g: Y → X such that g * f is homotopic to the identity map idX, and f * g is homotopic to idY. The maps f and g are homotopy equivalencies. Every homeomorphism is a homotopy equivalence but not vice versa. A function that is homotopic to a constant function is called null-homotopic. A space X is contractible if and only if the identity map from X to itself, which is always a homotopy equivalence, is null-homotopic.
If X and Y are homotopy equivalent spaces, then
1. If X is path-connected, then so is Y.
2. If X is simply-connected, then so is Y.
3. The singular homology and cohomology groups of X and Y are isomorphic.
4. If X and Y are path-connected, then the fundamental groups, as well as the higher homotopy groups, are isomorphic.
Later, I'll explain what these terms mean. You can define a homotopy category whose objects are topological spaces, and whose morphisms are homotopy classes of continuous maps. The topological spaces X and Y are isomorphic in this category if and only if they are homotopy equivalent.
The homotopy relative to a subspace is a homotopy which keeps the elements of the subspace fixed. If f and g are continuous maps from X to Y, and K is a subset of X, then f and g are homotopic relative to K if there exists a homotopy H : X x [0, 1] → Y between f and g such that H(k, t) = f(k) = g(k) for all k ∈ K and t ∈ [0, 1]. Also, if g is a retract from X to K, and if f is the identity map, this is called a strong deformation retract of X to K.
In mathematics, we want to do operations, proofs, algebra, etc, on the objects we're working with but it's very difficult to do these things on the topological spaces themselves. It's easy to do operations, proofs, algebra, etc, on groups since we understand groups very well. What we would like to do is somehow convert a topological space into a group so we could then work with the group. The search then is for groups that capture the essential information of a topological space. In addition, we would prefer groups that are easier to work with. This is the whole point of the subject of algebraic topology, which is to find groups that are easy to work with, which encapsulate all the information describing the topological space, so we can do algebraic operations on the groups, and it would be almost as if you are doing algebraic operations on the topological space. Usually, you can't find a group that captures all the information about a given topology but there are different groups that capture different amounts of information, or different kinds of information, about a topology, such as the fundamental group, higher homotopy groups, homology groups, and cohomology groups. By studying these groups, you can learn more about the topological space. You can see how this would be very useful in superstring theory where the particle spectrum and the low energy physics is determined by the details of the topology of the manifold that the extra dimensions are compactified on.
The first person to try to convert manifolds into groups was Felix Klein (1849 - 1925) who pioneered the most famous way of representing a manifold as a group, which is simply the group of symmetries of the manifold. An n-dimensional sphere, Sn, has the rotation group SO(n + 1). If you include reflections, you have O(n + 1). Felix Klein's book "Lectures on the Icosahedron" discusses subsets of that group. For n-dimensional Euclidean space, Rn, you have the Euclidean group ISO(n), which is the rotations in SO(n) combined with translations in Rn. Hyperbolic geometry has the group SO(n, 1) as symmetries. This is the same as the Lorentz group in special relativity. Projective geometry has the group SL(n + 1) as symmetries. This is the group of (n + 1) x (n + 1) matrices with determinant 1. Scalar multiples of the identity act trivially on projective space, so it's more accurate to use the projective general linear group PGL(n + 1).
The next simplest group you can have describing a topology is the fundamental group which is defined as follows. You start out by choosing a point somewhere on the topology which you then call the base point. You then, starting at the base point, travel in a path around the topology, and return to the base point, forming a closed loop. Two paths are considered equivalent if they can be deformed into each other without breaking. All possible paths, or closed loops starting and ending at the base point, then form a group called the fundamental group. The product of two loops is simply going around the first loop, and then going around the second loop, except that you're going around each loop twice as fast since it takes you as much time to go around the product of two loops as it does to go around each loop individually. The inverse of a path is simply traveling around the loop in the opposite direction. The identity is staying at the base point with no movement at all. In other words, all the possible distinct paths you can take around a topology, starting and ending at the base point, constitutes a group. If the topological space is path-connected, meaning it's possible to draw a path from any point to any other point, then it doesn't make any difference which point you choose to be the base point.
Let's write this down in mathematical notation. Let X be a topological space, and let x0 be a point on X. We are interested in a set of continuous functions f : [0, 1] → X, where it begins at time 0 and ends at time 1, where the function is located at the base point x0 at both times 0 and 1.
f(0) = f(1) = x0
These functions are called loops with base point x0. Two such loops f and g are considered equivalent if there is a continuous function h : [0, 1] x [0, 1] → X with the property that for all times t in [0, 1]
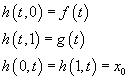
1. h(t, 0) = f(t)
2. h(t, 1) = g(t)
3. h(0, t) = h(1, t) = x0
In other words, the function h can deform the function f into the function g, so that at time 0, the function h is the same as the function f, and at time 1, the function h is the same as the function g. So you can imagine the loop f deforming into the loop g over time, and the functions f and g are equivalent if this is possible. Such a function h is called a homotopy from f to g, and the corresponding equivalence classes are called homotopy classes.
The product f * g of two loops f and g is defined by setting
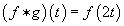
(f * g) (t) = f(2t)
if t is in [0, ½] and
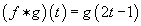
(f * g) (t) = g(2t – 1)
if t is in [ ½, 1]
The loop f * g thus first follows the loop f with twice the speed, and then follows g with twice the speed. The product of two homotopy classes of loops [f] and [g] is then defined as [f * g] and it can be shown that this product does not depend on the choice of representatives. With this product, the set of all homotopy classes of loops with base point x0 forms the fundamental group of X at the point x0, and is written π1(X, x0). The identity is the constant map at the base point, and the inverse of loop f is the loop g defined by g(t) = f(1 – t), so g follows f backwards. Although the fundamental group in general depends on the base point, this choice makes no difference if X is path-connected, so you can write π1(X) instead of π1(X, x0).
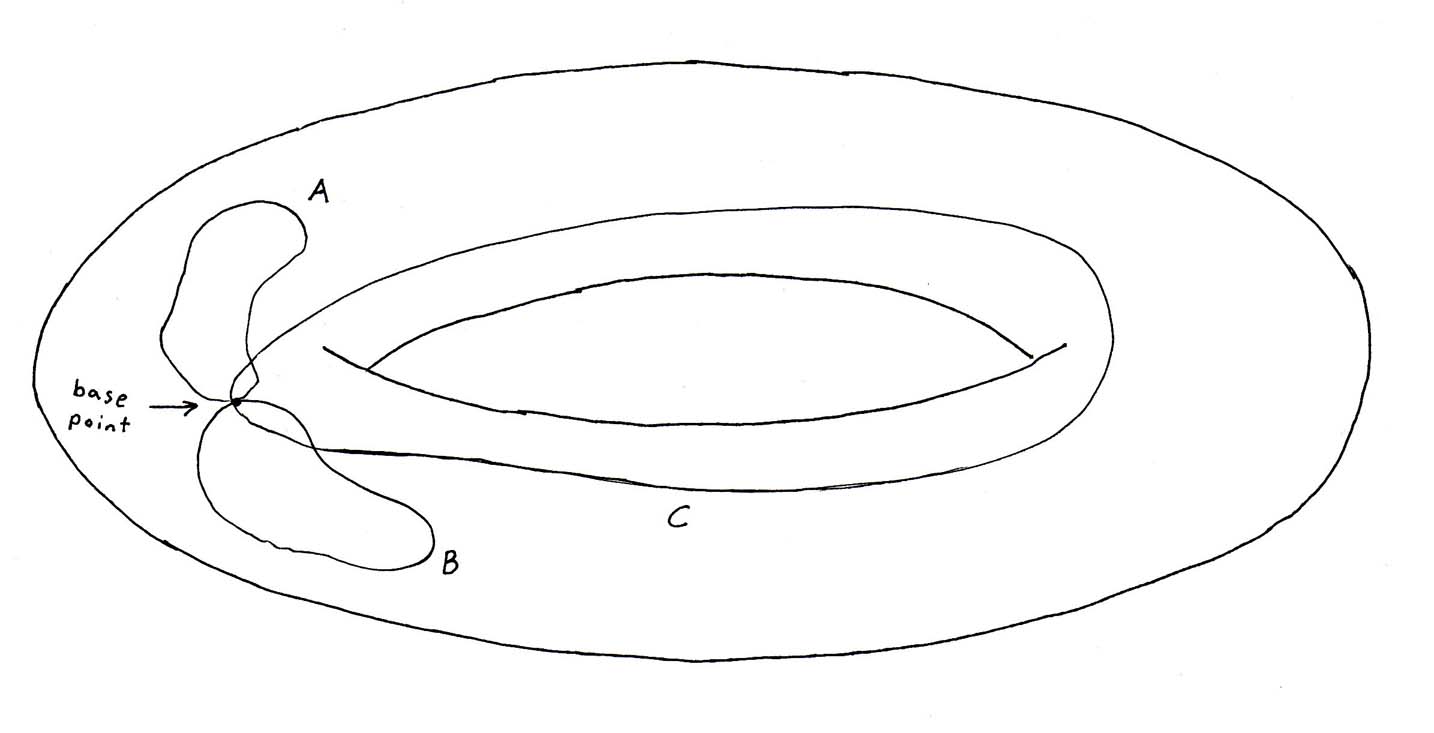
Here you have a torus with three possible loops drawn from a base point. Loops A and B can be deformed into each other, and could also be contracted to the base point. Loop C goes around the hole of the torus, and so could not be deformed into A or B, and can not be contracted to the base point. Therefore A and B are equivalent to the identity, while C is distinct. Notice that if we had used a sphere instead of a torus, then all loops could be deformed into each other, and all loops could be contracted to the base point.
There are some manifolds, such as a sphere or a plane, or any Sn or Rn, with n > 1, where any closed loop that could be drawn on the surface or in the space could always be contracted to a single point. In such a manifold, all loops, which are members of the group, can be contracted to the base point, and are thus equivalent to the identity, which is no movement at all. In other words, the group only has one member, which is the identity. This is the identity group which is the simplest possible group. A manifold on which any closed loop can be contracted to the base point is called simply-connected.
Then there are other manifolds where there is something the path can be taken around that prevents the loop from being shrunk to a single point. It could be a torus where the loop could wrap around the doughnut hole an integer number of times. A loop that wraps around the doughnut hole twice is distinct from a loop that wraps around it once. You would have the same thing with an infinite cylinder where the loop is perpendicular to the axis, or a punctured plane which is a plane with one point removed, or simply a circle, S1, where the path could go an integer number of times around the circle. Each homotopy class consists of all loops which wind around the circle a given number of times, which can be positive or negative depending on the direction of the winding. The product of a loop that winds m times and another that winds n times is a loop that winds m + n times. Therefore the fundamental group of a circle is isomorphic to (Z, +), the additive group of the integers. If you have a circle, S1, you could draw a path around the circle an integer number of times, so the fundamental group is the group of integers, represented by Z. In other words, π1(S1) = Z.
If you had a connected sum of two tori, which has genus 2, a loop could encircle one hole, or the other, or both of them, or do a figure eight between them, or any of the above any integer number of times. The greater the genus of the manifold, or the more boundaries or handles it has, the more complicated the resulting fundamental group.
The loop that forms the path that begins and ends at the base point, itself is topologically a circle, S1. You can generalize this process from using S1 to using Sn, which is a sphere of any dimension. The resulting group is called the n-th homotopy group. When the path is a circle, S1, the resulting group is the fundamental group, which is another name for the first homotopy group. You can use a sphere, S2, instead of a circle, S1, although in that case you can't visualize it as a path traced by a point, and the resulting group is the second homotopy group. If you use an n-dimensional sphere, Sn, it produces the n-th homotopy group πn(X). In the sphere, Sn, you choose a base point a. For a space X, with base point b, we define πn(X) to be the homotopy classes of maps f : Sn → X that map the base point a to the base point b. The equivalence classes are given by homotopies that are constant on the base point of the sphere. For n ≥ 1, the homotopy classes form a group. The first homotopy group, which is the fundamental group, is not abelian, but the higher homotopy groups, πn(X) with n > 1, are abelian. This is because in two or more dimensions, two homotopies can be rotated around each other.
The group operations are not as simple as those for the fundamental group. Consider two maps a : Sn → X and b : Sn → X which pass through ρ ∈ X. The product a * b : Sn → X is given by mapping the equator to the base point ρ. The northern hemisphere is mapped to the sphere by collapsing the equator to a point, and then it is mapped to X by a. The southern hemisphere is similarly mapped to X by b. The choice of direction of a loop in the fundamental group corresponds to a manifold orientation of Sn in a homotopy group. Therefore the inverse of a map is given by switching orientation of the sphere. By describing the sphere in n + 1 coordinates, switching the first and second coordinates, changes the orientation of the sphere. Switching orientation reverses the roles of inside and outside. The homotopy groups do not depend on the choice of base point. Higher homotopy groups are abelian. The base point is fixed, and because n > 1, the map can be rotated. With n = 1, meaning the fundamental group, it’s impossible to rotate the map while keeping the base point fixed.
If you have a closed manifold where any loop can be contracted to a point, that means there are no boundaries or handles, which means it's topologically a sphere. This is called the Poincare conjecture. This fact seems self-evidentially true but apparently it's so difficult to prove that it was one of the Clay Institute's Millennium Prizes. This was finally proven in 2006 by Grigory Perelman although he refused to accept any prize money because he doesn't care about money, and instead cares only about advancing mathematics. Actually, it's the 3D case that's particularly difficult. It's easy to prove in any other dimension.
A space with π(X) = 0 for all i ≤ n, is called n-connected. If X is n-1-connected, n > 1, then the Hurewicz homomorphism π(X) → Hn from the nth-homotopy group to the nth-homology group is an isomorphism.
When f : X → Y is a continuous map, then f* : πn(X) → πn(Y) is defined by taking the images under f of the spheres in X. The push forward is natural.
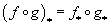
(f o g)* = f* o g
whenever the composition of two maps is defined. Given a fibration
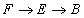
F → E → B
Where B is pathwise-connected, there is a long exact sequence of homotopy groups
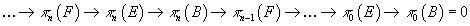
...→ πn(F) → πn(E) → πn → πn – 1(F) → ...→ π0(E) → π0(B) = 0
Here the maps involving π0 are not group homomorphisms because the π0 are not groups but they are exact in the sense that the image equals the kernel.
...→ πn(S1) → πn(S3) → πn(S2) → πn – 1(S1) →...
and the fact that πn(S1) = 0 for n ≥ 2, you have πn(S3) = πn(S2) for n ≥ 3. For instance, π3(S2) = π3(S3) = Z.
You also have relative homotopy groups πn(X, A) for a pair (X, A). The elements of such a group are relative homotopy classes of maps Sn → X. Two maps f and g are called homotopic to A if they are homotopic by a homotopy F : Sn x [0, 1] &rarr X such that for each a in A, the map F(a, t) is constant. Normal homotopy groups are then a special case where A is the base point.
If M and N are topological spaces, then for their direct product you have
πn(M x N) = πn(M) x πn(N)
If M is a simply-connected topological space, π0(M) = π1(M) = 0, and the group H acts on M, then you can form the topological space M/H identifying points of M which can be related by some elements H, where x = hx. You have
π11(M/H) = π0(H)
In particular, if H is a discrete group π0(H) and
π1(M/H) = H
For higher homotopy groups you have
πn(M/H) = πn(M)
if πn(H) = π(H) = πn – 1(H) = 0
For a circle
π1(S1) = Z
πn(S1) = 0
For higher dimensional spheres
πn(Sn) = Z
πk(Sn) = 0 for k < n
Here are the homotopy groups for Sn.
For a torus
π1(Tn) = (Z)n
πk(Tn) = 0 for k ≥ 2
For real projective space
π1(RP1) = Z
π1(RPn) = Z2 for n ≥ 2
πk(RPn) = πk(Sn) for k ≥ 2
For complex projective space
π1(CPn) = 0
π2(CPn) = Z
πk(CPn) = πk(S2n + 1) for k ≥ 3
I might mention in passing, the integers are symbolized by the letter Z because it stands for the German word "zahl" which means "to count". This is, however, different from Zn which is a symbol for an interval, which in that case stands for "Zyklus" which is the German word for "cycle". In group theory, I use "I" to mean the identity, but some people use "e" and the reason is because it stands for "Einheit" which is the German word for "identity". Later, I'll discuss K-theory, where K stands for "Klassen" which is the German word for "class".
The following capital English letters have π1(X) = 0 since they don't contain any closed loops.
C E F G H I J K L M N S T U V W X Y Z
The following capital English letters have π1(X) = Z since they have one closed loop.
A D O P Q R
The following capital English letter has π1(X) = Z x Z since it has two closed loops.
B
For the purpose of doing calculations in algebraic topology, a topological space is often approximated by a simplicial complex which is a lattice made up of points, line segments, triangles, tetrahedra, and their higher dimensional counterparts. A tetrahedron of arbitrary dimension is called a simplex, so triangles, tetrahedra, hypertetrahedra, etc, are types of simplices, and a lattice composed of these is a simplicial complex. For instance, a sphere could be approximated by an icosahedron which is then a simplicial complex in that it is composed of triangles. If the maximal dimension of the constituting simplices is k, then the complex is called a k-complex. An icosahedron would be a 2-complex. A simplicial complex is a combinatorial object telling you how to construct a topological space out of a number of simplices. A simplex by itself of dimension k is represented by labels called 0-simplices (its set of vertices), 1-simplices (line segments), 2-simplices (triangles), 3-simplices (tetrahedra), etc, all the way up to the single k-complex.
A simplicial complex is inadequate for some purposes, and so you can use a more general space called a CW-complex, which stands for closure finite weak complex. It involves gluing a closed n-dimensional ball Dn to the (n – 1)-skeleton Xn – 1, which is the union all lower dimensional cells. A 0-cell is just a point. If you have only 0-cells building up a Hausdorff space, it must be a discrete space. It must be closure finite, meaning each closed cell should be covered by a finite union of open cells. We require that a subset C ⊂ X is closed when the intersection of C with the closed cells in X is always closed. This is called weak topology.
Given X0 a discrete space, and inductively constructed subspaces Xi obtained from Xi - 1 by attaching some collection of i-cells, the resulting colimit space X is called a CW-complex provided it is given the weak topology, and the closure finite condition is satisfied by its closed cells.
The idea of a homotopy category is to start with a topological space category, which is one in which the objects are topological spaces, and morphisms are continuous mappings, and to replace the sets Hom(X, Y) of morphisms by sets of equivalence classes HOT(X, Y) that are defined by the homotopy relation. So the objects remain the same but the morphisms have been gathered into collections.
The homotopy category of CW-complexes is the best, if not the only, candidate for the homotopy category. For technical reasons, a homotopy category must keep track of base points in each space. For example, the fundamental group of a connected space is dependent on the base point chosen. A topological space with a distinguished base point is called a pointed space.

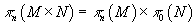
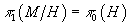
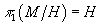
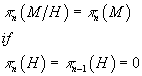
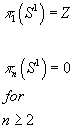
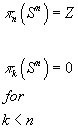
Sn
π1
π2
π3
π4
π5
π6
π7
π8
π9
π10
S1
Z
0
0
0
0
0
0
0
0
0
S2
0
Z
Z
Z2
Z2
Z12
Z2
Z2
Z3
Z15
S3
0
0
Z
Z2
Z2
Z12
Z2
Z2
Z3
Z15
S4
0
0
0
Z
Z2
Z2
Z x Z12
Z2 x Z2
Z2 x Z2
Z24 x Z3
S5
0
0
0
0
Z
Z2
Z2
Z24
Z2
Z2
S6
0
0
0
0
0
Z
Z2
Z2
Z24
0
S7
0
0
0
0
0
0
Z
Z2
Z2
Z24
S8
0
0
0
0
0
0
0
Z
Z2
Z2