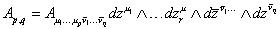
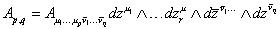
Ap,q = Au1…up[v bar]1…[v bar]q dzu1 /\ …dzru /\ d[z bar][v bar]1…/\ dz[v bar]q
Therefore, there are forms closed with respect to the holomorphic indices, anti-holomorphic indices, or both. The Betti numbers are bp, q. The complex version of Poincare duality is
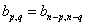
bp, q = bn - p, n - q
bp, q is the number of massless modes.
The simplest example of a Kahler manifold is the space Cn, which is n-tuples of the complex coordinates z1, z2… The Kahler potential φ is given by
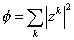
[phi] = [summation over k] | zk |2
This is not a compact manifold. To make it compact, you exclude the origin, and identify all points along lines passing through the origin. Let's say
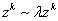
zk ~ [lambda]zk
for k = 1, 2…n, and you exclude the origin. The resulting manifold is called a CPn - 1 manifold. You have
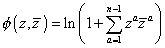
[phi](z, [z bar]) = ln (1 + [summation over a from 1 to n - 1] zz [z bar]a
This is not a Calabi-Yau manifold because the first Chern class of CPn - 1 is non-vanishing. Let's look at submanifolds of CPn which correspond to zero loci of homogenous polynomials.
Let's say you have a CPn manifold with homogenous polynomials pi = 0 of degrees q. You then have
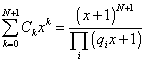
[summation over k from 0 to N + 1] Ck xk = (((x + 1)N + 1)/([product series over i] (qi x + 1))
where Ck are the Chern classes. The Calabi-Yau condition is C1 = 0. This gives
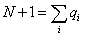
N + 1 = [summation over i] qi
As an example of a Calabi-Yau manifold, let's look at a CP4 space. You have the following constraint
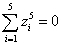
[summation over i from 1 to 5] zi5 = 0
Calabi-Yau manifolds have SU(n) holonomy. Let's say n = 3, so you have SU(3) holonomy. The Betti numbers bp, q for the Calabi-Yau manifold are
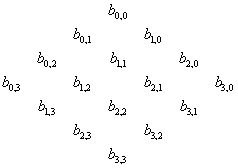
b_0,0
b_0,1 b_1,0
b_0,2 b_1,1 b_2,0
b_0,3 b_1,2 b_2,1 b_3,0
b_1,3 b_2,2 b_3,1
b_2,3 b_3,2
b_3,3
This is called the Hodge diamond. From the Poincare duality, each Betti number on the top half is equal to one in the mirror image position in the bottom half. You have b0, 0 = b3, 3, b0, 2 = b1, 3 , b0, 1 = b2, 3, etc.From this, you get
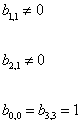
b1, 1 is not equal to 0
b2, 1 is not equal to 0
b0, 0 = b3, 3 = 0
The Euler characteristic of the manifold is given by
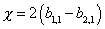
X = 2(b1, 1 - b2, 1)
For manifolds which are single CPn, b1, 1 = 1. For products of CPn, the manifold can be written as
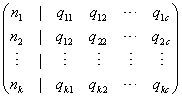
where qij is the power of the variable zi in the jth polynomial. The total Chern class for the manifold
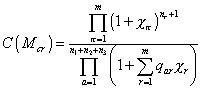
C(Mcr) = (([product series of pi from 1 to m] (1 + X[pi])nr + 1)/([product series of a from 1 to n1 + n2 + n3] (1 + [summation over r from 1 to m] qar Xr)))
In order to compute b1, 1, ignore the polynomials that mix the different CPn's.
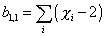
b1, 1 = [summation over i] (Xi - 2)
where χi is the Euler characteristic of the different submanifolds.
For a single CPn manifold with several polynomial constraints
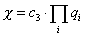
X = c3 . [product series of i] qi
where c3 is the coefficient of x3.
Let's look at a specific Calabi-Yau manifold. Let's look at the one proposed by Tian and Yau. It is given by
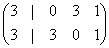
You have
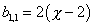
b1, 1 = 2(X - 2)
where χ is the Euler characteristic of the manifold. You get
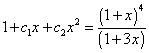
1 + c1x + c2x2 = ((1 + x)4)/(1 + 3x))
From this, you get c2 = 3, and χ = 9, so
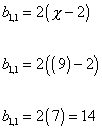
b1, 1 = 2(X - 2)
b1, 1 = 2(9 - 2)
b1, 1 = 2( 7 ) = 14
giving you b1, 1 = 14. The calculation of b2, 1 is done using deformation theory. It turns out that there is a one-to-one correspondence between the (2, 1)-forms and the independent polynomials by holomorphic transformations. These independent polynomials are independent complex structures of the manifold.
If you have the manifold proposed by Tian and Yau.
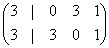
The total number of possible deformations is
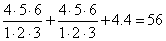
(4 x 5 x 6)/(1 x 2 x 3) + (4 x 5 x 6)/(1 x 2 x 3) + 4.4 = 56
Of these, 30 are related to the original polynomials by linear transformations, and three of the polynomials vanish. 56 - 30 - 3 = 23 Therefore, you have 23 independent complex structures, so b2, 1 = 23. So for this specific Calabi-Yau manifold, b 1, 1 = 14, and b2, 1 = 23. Therefore, the Euler characteristic of this specific Calabi-Yau manifold is
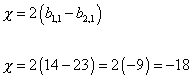
X = 2(b1, 1 - b2, 1)
X = 2(14 - 23) = 2(-9) = -18
Therefore, this Calabi-Yau manifold has a Euler characteristic of -18.
I have described the E8 x E8 heterotic superstring, and the Calabi-Yau manifold. Now, let's take the E8 x E8 heterotic superstring theory, and compactify the extra dimensions on the correct Calabi-Yau manifold. The theory has N = 1 supersymmetry. Since this means you have N = 1 supergravity, you therefore have one massless graviton, from the e in the Lagrangian, and one massless gravitino, from the ψn. The φ gives rise to a massless dilaton. The λ gives rise to the dilatino. You also have the antisymmetric tensor Bμν. The action involving this field has a gauge invariance. After the gauge degrees of freedom are removed, you have one pseudo-scalar field a, which can be identified with the axion.
Let's look at the gauge fields AMα, and their superpartners, the gaugino Xa in ten dimensions. Under E8 x E8, they transform as a
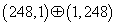
(248, 1) + (1, 248)
dimensional representation. Compactification that respects N = 1 supersymmetry requires that the gauge connection corresponding to the SU(3) subgroup be identified with the spin connection for the SU(3) part of the SO(6) group corresponding to the six compactified dimensions. Since the gauge field corresponding to the SU(3) subgroup has a non-zero vacuum expectation value, it breaks the gauge group E8 x E8 down to E8 x E6. Remember E8 has the following maximal subgroups.
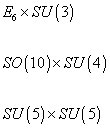
E6 x SU(3)
SO(10) x SU(4)
SU(5) x SU(5)
The gauginos and gauge fields corresponding to the broken E8 group have the following transformation properties under E6 x SU(3)
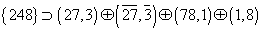
{248} is a subset of (27, 3) + ([27 bar], [3 bar]) + (78, 1) + (1, 8)
Since the SU(3) gauge group is identified with the spin connection, the SU(3) gauge group indices become indices of the compactified manifold. Let's divide the 10-dimensional spacetime index M into a spacetime coordinate u, and an internal coordinate m. The six m indices transform under SU(3) as
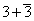
3 + [3 bar]
denoted by a and [a bar]. Then AMα contains A[α bar]α. Calabi-Yau manifolds with SU(3) holonomy have a covariantly constant antisymmetric tensor εabc. Multiplying by εabc, you can convert A[a bar]a into a (2, 1)-form
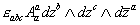
[epsilon]abc A[a bar]a dzb /\ dzc /\ d[z bar][a bar]
Therefore, the (27, 3) part of the gauge field-gaugino system corresponds to closed (2, 1)-forms. Therefore, b2, 1 counts the number of {27}-dimensional superfields. Similarly, in the ([27 bar], [3 bar]) part of AMα, you can isolate part which transforms like A[a bar][b bar] which can be converted into a (1, 1)-form
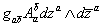
ga[b bar] A[a bar][b bar] dza /\ d[z bar][a bar]
Therefore, the number of massless {[27 bar]} superfields are given by the Betti-Hodge number b1, 1. The number of generations of the particles is
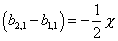
(b2, 1 - b1, 1) = -½ X
There is a one-to-one correspondence between (2, 1)-forms and the polynomial deformations, so you have an explicit representation for the quark and lepton fields.
The starting gauge group for grand unification with Calabi-Yau type compactification is E8 x E6, with low energy matter fields transforming as {27}, of which the total number is given by b2, 1 of the corresponding manifold, and {[27 bar]}, given by b1, 1 of the manifold. The whole thing is then coupled to N = 1 supergravity. From this, you get the following gauge group breakdown scheme.
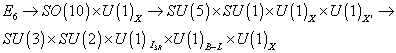
E6 -> SO(10) x U(1)X -> SU(5) x SU(1) x U(1)X x U(1)X' -> SU(3) x SU(2) x U(1)I3R x U(1)B - L x U(1)X
So the SU(3) group of the Calabi-Yau manifold breaks E8 x E8 to E8 x E6 . Then E6 breaks to the SO(10) group, which is SO(10) x U(1)X, which then breaks to the SU(5) group, which is SU(5) x SU(1) x U(1)X x U(1)X', which then finally breaks to the Standard Model, which is SU(3) x SU(2) x U(1)I3R x U(1)B - L x U(1)X.
In the following gauge group, you end up with the following particles.
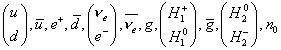
(u d), [u bar], e+, [d bar], ([nu], e-), [nu bar], g, (H1+ H10), [g bar], (H20 H2_), n0
where g is a g-quark, a new quark singlet, and n0 is another singlet fermion. This is the particle content of the 27-dimensional representation of E6. This is one generation. The number of fermion generations is given by
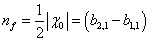
nf = ½ | X0 | = (b2, 1 - b1, 1)
The problem is the number of predicted generations is usually too big. If the Calabi-Yau manifold has a Euler number of -18, that would give ½ |-18| = 9 generations. We know from neutrino oscillations that there are only three generations. Therefore, you need a way to reduce to number of generations to three. Fortunately, you can reduce the Euler characteristic, χ0, of the Calabi-Yau manifold by choosing an appropriate discrete symmetry group H that acts freely on the manifold R0. It does not leave any point in the manifold fixed. The resulting manifold has the following Euler characteristic.
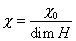
X = X0/(dim H)
Let's say you have a CP3 x CP3 manifold, and you have the following polynomials.
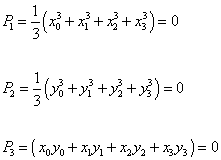
P1 = 1/3 (x03 + x13 + x23 + x33) = 0
P2 = 1/3 (y03 + y13 + y23 + y33) = 0
P3 = (x0y0 + x1y1 + x2y2 + x3y3) = 0
This Calabi-Yau manifold R0 has a Euler number of χ = -18, and thus nine generations. To reduce the number of generations, consider the Z3 group which acts freely on the manifold, and let it operate on the coordinates xi and yi where i = 0, 1, 2, 3
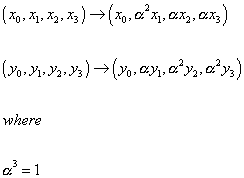
(x0, x1, x2, x3) -> (x0, [alpha]2 x1, [alpha] x2, [alpha] x3)
(y0, y1, y2, y3) -> (y0, [alpha] y1, [alpha]2 y2, [alpha]2 y3)
where
[alpha]3 = 1
This reduces χ to -6
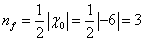
nf = ½ | X0| = ½ | -6 | = 3
so you have three generations of fermions. Therefore, if you compactify the extra dimensions on this specific Calabi-Yau manifold, you end up with three generations of quarks and leptons recognizable as the familiar particles from the Standard Model.
The discrete symmetry group H can also be used to break the gauge groups through symmetry breaking, which is good because otherwise the proton would have a lifetime of only 10-15 seconds. A function ψ acting on R is equivalent to a function on R0 if
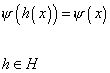
[psi] (h (x)) = [psi](x)
h is a member of H
Since the Lagrangian is E6-invariant, the following weaker condition is sufficient.
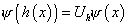
[psi] (h (x)) = Uh [psi](x)
where Uh is an element of the E6-group which provides a homomorphism of H into the group H6. Since under a gauge rotation
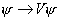
[psi] -> V[psi]
you have
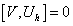
[V, Uh] = 0
The surviving group below the compactification scale is the one that commutes with the embedding of H in E6, and is therefore a smaller group.
In the process of compactification, all E6-gauge field strengths in ten dimensions must vanish. In a simply connected manifold, Fmn = 0 nears that of Am = 0 up to the gauge transformations. However, for a multiply connected manifold, this is not true since
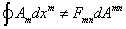
[path integral] Am dxm is not equal to Fmn dAmn
Since Am transforms as the adjoint representation of E6
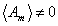
Am is not 0
reduces the gauge group without reducing its rank.
To use this for E6, you need functions of Am which are unitary operators such as
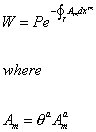
W = Pe(-[path integral around gamma]Amdxm) where
Am = [theta]a Ama
and where a is the E6 index, and γ is a closed loop in the multiply connected space. W is called the Wilson loop integral. When
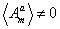
Ama is not 0
you have
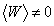
W is not 0
and it leads to a breakdown of the E6 symmetry.
For a Zn group, which is abelian, Wn = 1, and you can parametrize W as
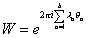
W = e2[pi]i[summation over a from 1 to b] [lambda]a[theta]a
where θa are elements of the Cartan subalgebra of the E6 group, λa are real parameters, and a = 1, 2,…6.
The mass of a gauge boson, whose weight factor is given by α is proportional to α. λ, where α is a six-component vector for the E6 group. When
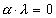
[alpha] . [lambda] = 0
you get an unbroken symmetry group. Using the root vectors of E6, in order to keep SU(3) x SU(2) x U(1) unbroken, λ must have the following form
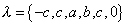
[lambda] = {-c, c, a, b, c, 0}
where a, b, and c are arbitrary constants. If they are totally arbitrary, the unbroken group is the Standard Model group SU(3) x SU(2) x U(1). If they are not totally arbitrary, the group that is unbroken is larger than the Standard Model group.
Here we have assumed that only abelian groups break E6. However, you can also consider non-abelian groups. An advantage of using non-abelian groups is that the breaking at the Planck scale also reduces the rank of the group so you could avoid the problem of rapid proton decay.
In order for the E6 type superstring models to be phenomenologically viable, you need at least one intermediate scale, and possibly two. There are three main points that have to be satisfied. First of all, baryon number violating processes must be suppressed to an acceptable level. Second of all, the evolution of coupling constants depends on the β-function for the gauge theory. As I said in the section on supersymmetry, the existence of extra fermions slows down the evolution of the coupling constants. In the E6 supergravity model, there is an extra quark called the g-quark. This causes the SU(2) coupling to grow beyond the electroweak scale while the QCD coupling is fixed beyond the electroweak scale. This could destroy the unification of the coupling constants. Third of all, the E6 group is left-right symmetric. Left-right symmetric models contain a right-handed neutrino that allows you to give masses to the neutrinos. However, all by itself, the mass of the neutrinos would be too large. You have to explain the great discrepancy between the masses of the neutrinos and the other leptons. The usual solution is the see-saw mechanism. However, in superstring theory, you can't use the normal see-saw mechanism. The solution to the first two problems is at least one intermediate scale. The solution to the third problem is to have a generalized see-saw mechanism.
Let's say you have the following compactification.
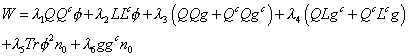
W = [lambda]1 Q Qc [phi] + [lambda]2 LLc [phi] + [lambda]3 (QQg + Qc Q gc) + [lambda]4 (QLgc + Qc Lc g) + [lambda]5 Tr [phi]2 n0 + [lambda]6 ggc n0
where
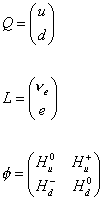
Q = (u, d)
L = ([nu], e)
Let's look at the baryon number interactions, which are the couplings λ3 and λ4. The g-quark acquires a mass of
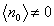
n0is not 0
The effective QQQL-type Hamiltonian is given by
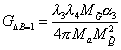
G[delta]B = 1 = ([lambda]3 [lambda]4 M[G tilda] [alpha]3)/(4[pi]Ma M[Q tilda]2)
Let's say
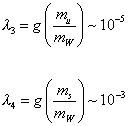
[lambda]3 = g(mu/mW) ~ 10-5
[lambda]4 = g(ms/mW) ~ 10-3
Then
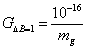
G[delta]B = 1 = 10-16/mg
Therefore
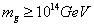
mg > 1014 GeV
Therefore you must have
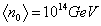
n0 = 1014 GeV
for baryon number violation to be consistent with experiment. Therefore, you need at least one intermediate scale. This would also solve the problem of the evolution of the coupling constants since the g-quark would start contributing to the evolution of the coupling constants only above 1014 GeV.
The problem of explaining the small neutrino masses is normally done by the see-saw mechanism which requires generating large Majorana masses, which requires a Higgs boson with a B - L quantum number 2. There is no such particle in string theory. Therefore, you can't use the normal see-saw mechanism. However, you can instead use a generalized see-saw mechanism by adjoining a 2-component chiral neutral lepton S to each pair of neutrino and anti-neutrino. You can then write the following 3 x 3 matrix.
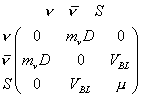
In order to generate the [ν bar]S entry, you need a Higgs boson with SU(2)R x U(1)B - L quantum number (½, 1), which is part of the {27}-dimensional representation of E6.
If VBL has a value of 1 TeV, for u = 10 - 100 GeV, then mν is acceptably small. S could be the B - L gaugino or any other E6 singlet. Therefore, by including an intermediate breaking scale, and a modified see-saw mechanism, you can solve the problems of baryon number violation, unification of the coupling constants, and smallness of neutrino masses. Therefore, there are no obvious phenomenological problems with E8 x E8 superstring theory compactified on a CP3 x CP3 Calabi-Yau manifold.
Therefore, if you take E8x E8 heterotic superstring theory, and compactify six of the ten dimensions on a specific Calabi-Yau manifold, CP3 x CP3, you get a theory that includes N = 1 supergravity, and thus the spin-2 graviton, Yang-Mills fields, and thus the spin-1 gauge bosons, and then through the 27-dimensional representation of E6, all the quarks and leptons of the Standard Model, in three generations, and also with a method of breaking the symmetry of the gauge groups through an intermediate scale that preserves the long proton lifetime. That is an amazingly impressive achievement.
At the same time, I don’t want to overstate the success of superstring theory. It wasn’t until 2002 that we could calculate scattering amplitudes at the two loop level. In 1982, Michael Green and John Schwarz were able to calculate scattering amplitudes of Type II strings at tree level and first loop. In 1986, Gross, Harvey, Martinec, and Rohm were able to calculate scattering amplitudes of the Heterotic string at tree level and first loop. In 2002, Eric D’Hoker and D. H. Phong were able to calculate scattering amplitudes of Type II and Heterotic strings up to second loop. The reason it took so long to go from one loop to two loops is that in the RNS formalism, there is the emergence from the gauge fixing procedure of odd Grassmann-valued supermoduli. They eventually solved this problem using a superspace formulation of the worldsheet. They gave a construction from first principles for an unambiguous and slice-independent two-loop superstring measure on moduli space for even spin structure.
In superstring theory, the extra dimensions are usually compactified on a Calabi-Yau manifold, although people have successfully compactified the extra dimensions on other manifolds, such as K3 or K3, which is a manifold with SU(2) holonomy, and even other types of topology, such as orbifolds. An orbifold is a slight generalization of a manifold that allows singularities. For instance, you could think of the rotation group G of a given polyhedron, which is a subgroup of the rotation group SO(3). Let's say you have R3, and define two points (x, y, z) and (x', y', z') to be equal if you can get from one to the other by a rotation in G. The resulting space is not a manifold. For instance, it has a singularity at the origin. However, it is an orbifold. In this example, it's called "R3 modulo the action of G".
Landau-Ginzburg models were originally used to describe phase transitions. A supersymmetric generalization of Landau-Ginzburg models has been studied in the context of superstring compactification. The expectation value of an n-tuple of fields is controlled by a potential, which in supersymmetric models, is the square of the magnitude of the gradient of a holomorphic function. This gives rise to an orbifold that extra dimensions can be compactified on. There are many Landau-Ginzburg orbifolds that give rise to identical physics as specific Calabi-Yau manifolds.
There are two basic ways of formulating superstring theory. You can put the supersymmetry on the two-dimensional string world sheet, which is called the Ramond-Neveu-Schwarz formalism, or the RNS formalism. You can also put the supersymmetry on the ten-dimensional spacetime that the strings are moving through, which is called the Green-Schwarz formalism, or the GS formalism. What we've been discussing so far has been the RNS formalism, which is much easier, and therefore more common, although it obscures the fact that the theory is truly supersymmetric in the traditional sense. The GS formalism is considerably more difficult technically, although the physics is perhaps more transparent.
The RNS formalism is easier because you are working in two dimensions, meaning the two dimensions of the world sheet. This world sheet supersymmetry also requires spacetime supersymmetry, which is what we're interested in, although the proof is long and difficult, and the supersymmetry is not manifest at the level of the action.
In the Green-Schwarz formalism, you are dealing directly with spacetime supersymmetry. In superstring theory, you have 10 dimensions, meaning eight degrees of freedom, which are eight transverse coordinates in the light cone gauge. The other two degrees of freedom can be eliminated by a gauge transformation. Therefore, you have eight bosonic degrees of freedom, and you need to get eight fermionic degrees of freedom in order to have the same number of bosonic and fermionic degrees of freedom. However, a spinor in 10 dimensions has 32 complex components. If you impose Majorana and Weyl conditions, you can reduce this to 16. The resulting representation of the Lorentz group is irreducible. How do you then reduce the number of fermionic degrees of freedom from 16 to 8?
Fortunately, there exists a type of symmetry called kappa symmetry, or κ-symmetry, originally proposed by Seigel, under which half of the fermionic degrees of freedom can be gauged away. In 1981, Michael Green and John Schwarz found an action with kappa symmetry, that they used to gauge away half of the fermionic degrees of freedom, reducing the number of fermionic degrees of freedom from 16 to 8, so you ended up with the same number of bosonic and fermionic degrees of freedom. You end up with an action with manifest supersymmetry.
This is the advantage over the RNS formalism. However, the RNS and GS formalisms are equivalent to each other. Most string theorists work in the RNS formalism because gauge fixing the kappa symmetry is extremely difficult. If you want to preserve manifest Lorentz invariance, you end up with an infinite number of ghosts.
Let's discuss the GS formalism of superstrings in more detail. Let's start with the N = 1 and N = 2 superspaces which are identified with the supertranslation groups. The supertranslation algebras are spanned by the 10-momentum Pu, and one or more Lorentz spinor charges. The minimal spinor in d = 10 is Majorana and chiral. A Majorana spinor Q is one for which
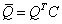
[Q bar] = QT C
where the bar represents the Dirac conjugate, and C is the antisymmetric real charge conjugation matrix. There exists a representation of the Dirac algebra called the Majorana representation in which the Dirac matrices are real. In this representation
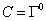
C = [capital gamma]0
and a Majorana spinor is a real 32-component spinor. A chiral spinor Q is one for which
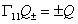
[capital gamma]11 Q± = ± Q
where Γ11 is the product of all ten Dirac matrices. It satisfies
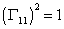
([capital gamma]11)2 = 1
and is therefore real in the Majorana representation. A chiral Majorana spinor has 16 independent real components.