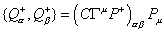
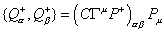
{Q[alpha]+, Q[beta]+} = (C[capital gamma]u P+)[alpha][beta]Pu
where Q+ is a chiral Majorana spinor, Pu is the 10-momentum, and P+ projects onto the positive chirality subspace. The choice of positive or negative chirality is a convention. An element of the supertranslation group is obtained by exponentiation of the algebra element
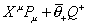
Xu Pu + [theta bar]+ Q+
where Xu are d = 10 spacetime coordinates, and θ+ is an anti-chiral and anticommutating Majorana spinor coordinate. There are two N = 2 supertranslation algebras, according to whether the two supersymmetry charges have the same or opposite chirality. If they have opposite chirality, you can assemble them into a single non-chiral Majorana charge Q. This leads to the IIA algebra.
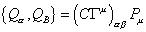
{Q[alpha], Q[beta} = (C[capital gamma]u)[alpha][beta] Pu
If the two supersymmetry charges have the same chirality, you can assemble them into the SO(2) doublet Q+I, where I = 1, 2. You then get the IIB algebra.
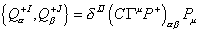
{Q[alpha]+I, Q[beta]+J} = [delta]IJ (C[capital gamma]u P+)[alpha][beta] Pu
With these supertranslation algebras, you can then construct superstring world sheet actions in the Lorentz covariant Green-Schwarz formulation, where the fields are maps from the world sheet to the superspace. You need the following supertranslation invariant superspace 1-forms on the three possible superspaces.
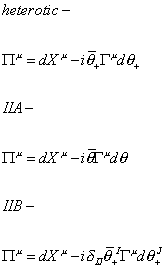
heterotic-
[capital pi]u = dxu - i[theta bar]+ [capital gamma]u d[theta]+
IIA-
[capital pi]u = dxu - i[theta bar] [capital gamma]u d[theta]
IIB-
[capital pi]u = dxu - i[delta]JJ [theta bar]+I [capital gamma]u d[theta]+J
The first is heterotic. The second is IIA. The third is IIB. The N = 1 superspace case is relevant to the heterotic strings. The Type I superstring is derived from the IIB superstring. The world sheet coordinates are
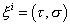
[xi]i = ([tau], [sigma])
and
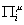
[capital pi]iu
is the 10-vector components of the induced world sheet 1-forms. In the heterotic case, you have
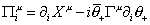
[capital pi]iu = [partial derivative]iXu - i[theta bar]+ [capital gamma]u [partial derivative]i [theta]+
where
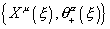
{Xu([xi]), [theta]+[alpha] ([xi])}
are the world sheet fields.
If you set the string tension to one, you can then write the Nambu-Goto action
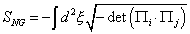
SNG = -[integral] d2 [xi] [squareroot of (-det ([capital pi]i . [capital pi]j)]
This is not the complete action because you also need a Wess-Zumino term. To construct it, you need super-Poincare closed forms in superspace. You need the following 3-forms

heterotic-
h(3) = [capital pi]u d[theta bar]+ [capital gamma]u d[theta]+
IIA-
h(3) = [capital pi]u d[theta bar] [capital gamma]u [capital gamma]11 d[theta]
IIB-
h(3) = [S tilda]JJ [capital pi]u d[theta bar]+I [capital gamma] d[theta]+J
where Γ11 is the product of the ten Dirac matrices Γu, and [S tilda]JJ are the entries in the following 2 x 2 matrix.
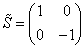
In the above 3-forms, the first is for the heterotic. The second is for IIA. The third is for IIB. Next, you need the heterotic 7-form.
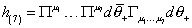
h(7) = [capital pi]u1…[capital pi]u7 d[theta bar]+ [capital gamma]u1…u7 d[theta]+
These forms are closed due to Dirac matrix identities valid in d = 10 so locally you can write h = db.
Given a (p + 2)-form h(p + 2), you can write to a super-Poincare invariant Wess-Zumino type action for a p-dimensional object, or p-brane, by integrating the (p + 1)-form b(p + 1) over the (p + 1)-dimensional world volume. Thus h(7) = db(6) is relevant to 1-branes, meaning strings. You can now write down the Wess-Zumino term in the GS superstring action
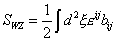
SWZ = ½ [integral] d2 [xi] [epsilon]ij bij
The combined action is the sum of the Nambu-Goto and Wess-Zumino actions.
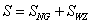
S = SNG + SWZ
The combined action has a fermionic gauge invariance called kappa symmetry or κ-symmetry, which allows half of the components of θ to be gauged away. When you choose a physical gauge, half of the original spacetime symmetries are linearly realized world sheet supersymmetries. Without κ-symmetry, they would be non-linearly realized. Thus, κ-symmetry is essential for equivalence with the world sheet supersymmetric RNS formalism of superstring theory.
The type II superstrings are closed strings whose covariant GS action is just S = SNG + SWZ, and for which the world sheet fields are all periodic. The fermions are actually world sheet scalars in this formalism. They become world sheet spinors only after gauge-fixing the κ-symmetry. The heterotic strings are closed strings based on the action S = SNG + SWZ for N = 1 superspace, but because of conformal invariance of the first quantized string, you also need a heterotic action involving 32 world sheet chiral fermions.
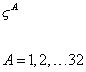
[zeta]A A = 1, 2,…32
If you choose these to transform as half-densities, then the heterotic action is
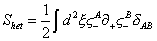
Shet = ½ [integral] d2 [xi] [zeta]A [partial derivative]+ [zeta]-B [delta]AB
where ∂+ is a chiral world sheet derivative. Therefore, the GS action for the heterotic string is
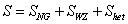
S = SNG + SWZ + Shet
The world sheet fermions ζA could be periodic or anti-periodic, so there seem to be many possible sectors in the full Hilbert space of the first quantized string. However, quantum consistency reduces the choices to the SO(32) and E8 x E8 heterotic strings.
There are many times when you are teaching somebody something, and you say something that is technically inaccurate, but is sufficiently accurate for the purpose, and then when the student reaches a more advanced level, they learn a more accurate version. In elementary school, the orbits of the planets are described as circular. In high school, they are described as ellipses. In college, a student might learn that they are actually egg-shaped, with the pointy end pointing to the Sun. A professional planetary astronomer calculating the positions of the planets with extreme precision would have to take into account the gravitational attraction of all the other planets and smaller bodies in the solar system. This is not to say you are lying to the elementary or high school students. What you tell them is sufficiently accurate for the purpose. Another example is in my paper on the Standard Model when I said that QCD predicts quark confinement, meaning quarks are permanently bound inside hadrons, or least have been since shortly after the Big Bang. However, according to some recent theories, you could have quarks outside of hadrons today, in certain neutron stars called quark stars, or even briefly in particle accelerators. However, you should not tell that to someone who is trying to learn QCD since the whole idea of QCD is to explain quark confinement. You don't want to confuse someone who is just beginning to learn it.
We have reached a point where I should probably mention that the names of the gauge groups that are commonly used by particle physicists are not actually technically accurate. Particle physicists use the names all the time but a mathematician would complain that the commonly used names are not the names of the actual groups involved. Mathematicians usually demand a higher level of technical accuracy in the nomenclature then physicists. A Lie algebra is a logarithm of a Lie group, and a Lie group is an exponential of a Lie algebra. There are several different Lie groups that have the same Lie algebra. What we have been calling the Standard Model gauge group SU(3) x SU(2) x U(1) is more accurately described as
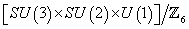
[SU(3) x SU(2) x U(1)]/Z6
All of the SU(n) groups we have mentioned are actually SU(n)/Z6. For instance, SU(5) is really SU(5)/Z6. What we have been calling SO(10) is actually Spin(10). The E8 x E8 group is actually the semi-direct product
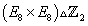
(E8 x E8) [triangle] Z2
where Z2 acts by exchanging the E8 factors. The SO(32) group of Type I and Heterotic SO(32) superstring theory is actually
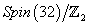
Spin(32)/Z2
also called Semispin(32). However, there is something different about this last example, which is that there is a downside to confusing the group you call it with the group it really is. With all the other examples, it does not make any difference. One group is called the cover for the other. That means you can use the technically inaccurate names with no negative repercussions.
For instance, SO(10) grand unification uses a certain 16-dimensional multiplet that does not correspond to any representation of SO(10). It is actually a representation of Spin(10). However, you can just use the name SO(10) to mean Spin(10). There is no harm done. Every representation of SO(10) is automatically a representation of Spin(10), because Spin(10) is a cover for SO(10). Similarly, you can write SU(3) x SU(2) x U(1) for [SU(3) x SU(2) x U(1)]/Z6 since every representation of the latter is a representation of the former. However, you can not do that with SO(32) and Spin(32)/Z2 because neither is a cover for the other. Both have representations which can't be regarded as representations of the other.
The T-duality of the two heterotic string theories relies on relating E8 x E8 and SO(32) through their supposed common subgroup SO(16) x SO(16). However, no such common subgroup exists. Not only that, but neither of the actual representative subgroups covers the other. Furthermore, each has representations which are not representations of the other, but which are crucial in establishing T-duality. Also, you have Wilson loops which behave in a way that depends very delicately on the various subgroups of Spin(32)/Z2 and Spin(16)/Z2. The local simplicity of the duality arguments conceals considerable complexity at the global level. Therefore, in the case of the so-called SO(32) group of superstring theory, there is good reason to remember that the actual group is Spin(32)/Z2, also called Semispin(32). That said, unless you are dealing with the finer points I mentioned above, most string theorists usually just go ahead and call it SO(32), while keeping in mind that really it's not.
The five superstring theories are related to each other by the T, S, and U dualities. This turned out to be a clue of the next great advance in superstring theory that took place during the second superstring revolution, starting in 1994. It turned out that the five superstring theories are all just different manifestations of one single underlying theory. This is a good thing since we would rather have one instead of five fundamental theories of the Universe. Also, this opened the door to discussing string theory non-perturbatively, and it was assumed that the perturbative expansion is not the whole story, and you would have to take non-perturbative effects into account in order to get an accurate view of the Universe. In string theory, the coupling constant, gs, is determined by the expectation value of a scalar field called the dilaton. There is no reason to assume it's small, which you have to do in order to assume that the perturbative expansion is an accurate approximation. The five string theories turn out not to be distinct theories. Instead, each of the five theories represents a perturbative expansion of a single underlying theory about a distinct point in the moduli space of the quantum vacua. Interestingly, there is also a sixth point in the moduli space that corresponds to an 11-dimensional supergravity theory. Unfortunately, both the 11-dimensional supergravity theory and the underlying theory are called M-theory. This is unfortunate terminology since you should not confuse them. The 11-dimensional supergravity theory is not any more fundamental than the five string theories. Some authors have thought up various different names to call them, in an attempt to distinguish them, and avoid confusion, but so far, there is no consensus. Usually, it's obvious from the context. I will usually refer to the fundamental underlying theory as M-theory, and call the other one 11d supergravity. You might also wonder, what does the "M" stand for? In fact, nobody knows. Different people claim that the "M" stands for magic, mystery, meta, matrix, membrane, murky, or mother of all theories.
However, this lack of understanding or consensus about what the "M" stands for, or what the word "M-theory" refers to, is perhaps appropriate. M-theory is literally the most advanced theory in all of physics. This is our current view of the Universe. You can look at the history of particle physics starting with the ancient Greeks, and go all the way up to M-theory, which is the most advanced theory that humanity has yet achieved. M-theory is the most advanced theory we currently possess. However, one aspect of that fact is that it is such a recent development, we haven't figured out what exactly it is yet. Therefore, when studying M-theory, you are witnessing physics in progress, as we are in the process of figuring out what exactly it is.
The five string theories are well understood as perturbation expansions. They have consistent perturbation expansions of on-shell scattering amplitudes. The type II and the heterotic string theories have only closed strings so they have particularly simple perturbation expansions. There is a unique Feynman diagram at each order of the loop expansion. The Feynman diagrams are world sheets. A given L-loop diagram is a closed orientable genus-L Riemann surface. Incoming and outgoing particles are represented by N punctures on the surface.

A given diagram represents a well-defined integral of dimension 6L-2N-6, where L is the genus of the world sheet, and N is the number of punctures, meaning the number of incoming and outgoing particles. The integral contains no divergences, despite containing the spin-2 graviton. String and supersymmetry contributions are responsible for amazing cancellations. Type I superstring theory contains both open and closed strings, so the perturbation expansion is more complicated. Various world sheet Feynman diagrams at a given order have to be combined to cancel divergences and anomalies.
T-duality can be understood perturbatively. This duality is between two string theories where one spatial dimension is compactified on a circle. It also holds true for more complex manifolds, such as Calabi-Yau manifolds, but obviously it's easiest talk about in the context of a simple manifold with one dimension compactified on a circle. Let's say you have two superstring theories A and B, each on a R9 x S1 manifold. If the radius of the circles that the extra dimensions are compactified on are RA and RB, then you have
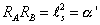
RA RB = ls2 = [alpha]'
where ls is the string length, and α' is the universal Regge slope, which is the string length squared. T-duality means that shrinking the circle to zero in one theory corresponds to expanding the circle in the other theory. Type IIA and Type IIB superstring theories are T-dual. This means that if you take the non-chiral Type IIA superstring theory, and compactify one dimension on a circle of radius R, and let R go to zero, it turns into the Type IIB theory in ten dimensions.
Instead of thinking of them as two theories that are related, you could instead think of them as only one theory. What we call two theories are just two points on a continuous spectrum. The radius R is actually the vacuum value of a scalar field, which arises as an internal component of the 10d metric tensor. Therefore, the Type IIA and Type IIB superstring theories are just two limiting points on a continuous moduli space of quantum vacua. The two heterotic superstring theories are also T-dual, although in that case, it's more complicated because of the different gauge groups. If you apply T-duality to Type I superstring theory, it turns into an unusual variation of itself called Type IA or Type I'.
In the 1970's, many people were working on point particle theories of supergravity, totally independent of string theory. In these theories, making supersymmetry a local symmetry naturally led to a spin-2 particle that could be identified with the graviton. However, these theories were non-renormalizable, as were all pre-string attempts to quantize gravity. In 1978, Cremmer, Julia, and Sherk developed a specific supergravity theory that existed in 11 dimensions. It had 32 conserved charges, and three kinds of fields. The first is the graviton field with 44 polarizations. The second is the gravitino field with 128 polarizations. The third is a three index gauge field, Cμνρ, with 84 polarizations. The supergraviton is a quantum mechanical mixture of these fields. Of course, 11d supergravity is non-renormalizable. 11-dimensional supergravity does not have a perturbation expansion. Also, it did not seem to have a mechanism for generating chiral fermions. Therefore, it did not seem promising that it would be an important theory.
However, early on, some people noticed a possible connection between the 11d supergravity and Type IIA superstring theory. The IIA supergravity and the 11d supergravity were similar. The main difference was that 11d supergravity was 11-dimensional, and the Type IIA supergravity was 10-dimensional. There was some sort of subtle connection between these two very different theories that remained a curiosity for many years. In 1987, Bergshoeff, Sezgin, and Townsend tried to rework the 11d supergravity theory as a theory of two-dimensional membranes analogous to superstring theory which was a theory of one-dimensional strings. The field equations of 11d supergravity admit a solution that describes a supermembrane. The energy density is concentrated in a two-dimensional surface. A 3d world volume description of the dynamics of this supermembrane is analogous to the 2d world volume actions of superstrings. They couldn't really get this theory of supermembranes to work, but it further pointed to a connection between the 11d supergravity and superstrings. Then it was realized that if you take this theory, and just reduce the dimension of the supermembrane world volume, you get the previously known Type IIA superstring world volume. This seemed to strongly suggest something profound, but no one could figure out what exactly it was, and again it remained a tantalizing puzzling curiosity. Then in 1995, P. K. Townsend and Edward Witten made a major breakthrough. In a shocking discovery, they determined that the Type IIA superstring theory really is 11-dimensional. Everyone had always thought it was 10-dimensional, but the whole time, it was actually 11-dimensional. It turned out that Type IIA superstring theory actually has an 11th dimension compactified on a circle, in addition to the previously known 10 dimensions. The reason why nobody had noticed this before is because it was a non-perturbative effect, and the theory had only been studied perturbatively.
The 11-dimensional supergravity, and thus M-theory, has no dimensionless parameters. The only parameter is the 11-dimensional Newton constant, which raised to the power of -1/9 gives the 11-dimensional Planck mass, mp. When M-theory is compactified on a circle, the spacetime geometry is R10 x S1, so you have another parameter, which is the radius of the circle. The parameters of Type IIA superstring theory are the string mass scale, ms, and the dimensionless string coupling constant, gs. Therefore, you can identify compactified M-theory with Type IIA superstring theory by
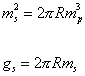
ms2 = 2[pi]Rmp
gs = 2[pi]Rms
where mp is the Planck mass, ms is the string mass scale, gs is the string coupling constant, and R is the radius of the circle that the 11th dimension is compactified on. You then have
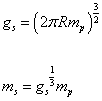
gs = (2[pi]Rmp)3/2
ms = gs1/3 mp
Therefore, the Planck length is shorter than the string length scale at weak coupling by a factor of (gs)1/3.
In traditional superstring theory, you have a perturbation expansion in powers of gs at fixed ms. This is equivalent to an expansion about R = 0. The strong coupling limit of Type IIA superstring theory corresponds to decompactification of the 11th dimension. If you have Type IIA superstring theory, and take the coupling constant gs to infinity, you end up with M-theory. Therefore, M-theory is Type IIA superstring theory at infinite coupling. You see how the 11th dimension would not be detected in string perturbation theory, which is at low coupling.
M-theory is a theory of membranes which are two-dimensional surfaces. It turns out that if you take an M2-brane of M-theory, and wrap one of its dimensions around the compact circular dimension, it looks the same as a superstring in Type IIA theory. Therefore, Type IIA superstrings actually are M-theory M2-branes with one of their dimensions wrapped around the 11th dimension which is compactified on a circle. If the string tension, TF1, is the energy per unit length, and the membrane tension, TM2, is the energy per unit volume, they are related by
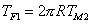
TF1 = 2[pi]RTM2
Also, you have
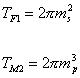
TF1 = 2[pi]ms2
TM2 = 2[pi]mp2
From this, you get
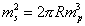
ms2 = 2[pi]Rmp3
At high coupling, Type IIA theory becomes 11-dimensional, where the 11th dimension is compactified on a circle. At low coupling, the radius of the circle is too small for it to be noticed. This is similar to the analogy I gave earlier with the garden hose. The E8 x E8 heterotic superstring theory also becomes 11-dimensional. In that case, the extra dimension is a line segment between the two 10-dimensional boundaries. Imagine you had two parallel planes separated by a line segment. If the line segment was very small, it would look like a plane. As the line segment got longer, you notice it was a three-dimensional space bounded by two planes. Here you have two 10-dimensional spaces separated by a line segment. At the low coupling, the line segment is short, and you think it's 10-dimensional space. At high coupling, the line segment gets longer, and you realize it's 11-dimensional space bounded by two 10-dimensional spaces. In E8 x E8 superstring theory, you have one E8 current algebra on each of the two 10-dimensional string boundaries. The string coupling is
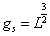
gs = L3/2
where L is the length of the line segment.
Even though people talk about these theories becoming 11-dimensional, they are really always 11-dimensional. You just don't notice the 11th dimension at weak coupling, meaning perturbatively. We know that the Type IIA superstring theory and the 11-dimensional supergravity are really the same theory. We know Type IIA superstring theory and E8 x E8 Heterotic superstring theory are really 11-dimensional. We know from T-duality, that the two Type II superstring theories are really the same theory, and the two heterotic string theories are really the same theory. We know from S-duality, that the Type I superstring theory and the SO(32) Heterotic superstring theory are really the same theory. Therefore, we know that all the five superstring theories, and also the 11-dimensional supergravity theory, are all really the same theory, and that one theory is 11-dimensional.
Since M-theory is a theory of membranes, this then ties in with D-branes, which I described earlier as a recent feature of superstring theory. If you want to specify the dimension of a D-brane, you call it a Dp-brane, where p is the dimension. The world volume swept out by a Dp-brane has p + 1 dimensions. The tension of a D-brane is given by
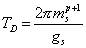
TD = (2[pi]msp + 1)/gs
Notice that the tension depends on the coupling constant. The D-branes carry a charge that couples to a gauge field in the RR sector of the theory. p takes even values in IIA theory, and odd values in IIB theory.
The D2-brane of Type IIA superstring theory corresponds to the supermembrane of M-theory with one of its dimensions compactified on a circle. The tension is
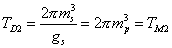
TD2 = (2[pi]ms3)/gs = 2[pi]mp3 = TM2
where TD2 is the tension of the D2-brane, TM2 is the tension of the M2-brane, ms is the string mass scale, mp is the Planck mass, and gs is the string coupling constant. The mass of the first Kaluza-Klein excitation of the 11d supergraviton is 1/R, which can be identified with the D0-brane. Every p-brane has a magnetic dual. The magnetic dual of a p-brane in d dimensions is a (d - p - 4)-brane. So for a D2-brane, which is the membrane in M-theory, you have

(d - p - 4)
( (11) - (2) - 4) = 9 - 4 = 5
This is called an M5-brane. It's tension is
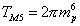
TM5 = 2[pi]mp6
If you wrap one of its dimensions around a circle, you get a D4-brane with tension
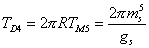
TD4 = 2[pi]RTM5 = (2[pi]ms5)/g5
where R is the radius of the circle. Let's look again at the M5-brane without one of its dimensions wrapped around the circle. This is called the NS5-brane of the IIA theory, which has the tension
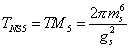
TNS5 = TM5 = (2[pi]ms6)/gs2