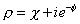
Type IIB superstring theory, which is also an 11-dimensional maximally supersymmetric string theory with 32 conserved supercharges, is chiral, meaning parity violating. At low energy, Type IIB superstring theory is approximated by Type IIB supergravity, similar to how M-theory is approximated by 11d supergravity. Type IIB superstring theory or supergravity has two scalar fields, the dilaton φ, and the axion X. These are combined together to form a complex field
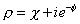
p = X = ie-[phi]
SL(2, R) is the set of all two-by-two matrices over the real numbers with determinant 1. You can also have SL(2, C) or SL(2, Z). “S” is for special, meaning unitary, determinant 1, “L” is for linear, “2” is a reference to 2 x 2 matrices, “R” is for real numbers, “C” is for complex numbers, and “Z” is for integers. The supergravity approximation has an SL(2, R) symmetry that transforms non-linearly
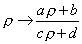
p -> (ap + b)/(cp + d)
where a, b, c, and d are real numbers satisfying
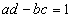
ad - bc = 1
This is called a Mobius transformation. In the quantum string theory, this symmetry is broken to the discrete subgroup SL(2, Z), which means that a, b, c, and d are integers.
The vacuum value of the p field is
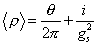
= ([theta]/2[pi]) + i/gs2
The SL(2, Z) transforms p → p + 1 which implies that θ is an angular coordinate. If θ = 0, then
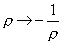
p -> -1/p
means
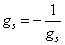
gs = -1/gs
which is what we've been calling S-duality. In Type IIB superstring theory, the coupling constant gs is the same as the coupling constant 1/gs, which means that Type IIB theory is self-dual under S-duality. The weak coupling expansion is the same as the strong coupling expansion. S-duality also relates Type I superstring theory to SO(32) heterotic superstring theory.
The name S-duality originates in the fact that the complex field
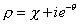
p = X + ie-[theta]
that parametrizes SL(2, R)/U(1) was called the superfield S.
Type IIA and Type IIB superstring theories are related by T-duality, meaning if they are compactified on a circle of radii RA and RB, then RARB = ls2. Type IIA superstring theory is actually M-theory compactified on a circle. If you combine these two facts together, it turns out that Type IIB superstring theory compactified on a circle, R9 x S1, is equivalent to M-theory compactified on a torus, R9 x T2.
You could say that all the superstring theories are really one 11-dimensional theory at a fundamental level, so Type IIB superstring theory is really 11-dimensional, say with one dimension compactified on a circle, giving the familiar 10-dimensional theory. Then take that 10-dimensional Type IIB theory, and compactify one of its dimensions on a circle, giving R9 x S1. Then take M-theory, which is obviously 11-dimensional, and compactify two of its dimensions on a torus, giving R9 x T2. There is a duality between these two theories, and they are related by
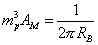
mp3 AM = ½[pi]RB
where mp is the Planck mass, AM is the area of the torus that two of the dimensions of M-theory are compactified on, and RB is the radius of the circle that one of the dimensions of Type IIB theory are compactified on. As the radius of the circle gets smaller, the area of the torus gets larger. As the area of the torus gets larger, the radius of the circle gets smaller. As the circle gets larger, the torus gets smaller. As the torus gets smaller, the circle gets larger. You see how this is analogous to T-duality, and therefore, Type IIB theory and M-theory are also one theory.
With S-duality, theory A at strong coupling is equivalent to theory B at weak coupling, and vice versa. If φ is the dilaton field, you have
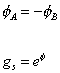
[phi]A = -[phi]B
gs = e[phi]
With T-duality, theory A compactified on a space of large volume is equivalent to theory B compactified on a space of small volume, and vice versa. If t is a scalar field other than the dilaton, you have
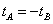
tA = -tB
With U-duality, theory A compactified on a space of large volume is equivalent to theory B at strong coupling. Theory A compactified on a space of small volume is equivalent to theory B at weak coupling. You have
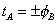
tA = ±[phi]B
With each of these dualities, the two theories are really different descriptions of the same theory.
In supergravity theories that represent the low energy effective action for the massless modes of a superstring compactification, you have a non-compact global symmetry group G. The group G is realized non-linearly by scalar fields that parametrize the homogeneous space G/H, where H is the maximal subgroup of G. The first example of this phenomenon, with G = SL(2, R), and H = U(1), was discovered by Cremmer, Ferrara, and Scherk in 1976, in the N = 4 supergravity. A discrete subgroup of symmetry of this particular example corresponds to the S-duality that was first seen in string theory, the toroidally compactified heterotic string. Then an analogous non-compact E7 symmetry was found in N = 8 supergravity by Cremmer and Julia in 1978. This corresponds to the toroidally compactified Type II string, and combined S, T, and U dualities in a single group.
In 1990, Font suggested that the SL(2, Z) subgroup of SL(2, R) of Cremmer, Ferrara, and Scherk should be the exact same symmetry as the toroidally compactified heterotic string. This proposal extends the duality conjecture of Montona and Olive from supersymmetric gauge theories to superstrings. Let's look at S duality, which is usually written
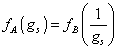
fA(gs) = fB(1/gs)
This has a subtle similarity to the electric and magnetic fields in an electromagnetic wave, according to classical electromagnetism. For this reason, this sort of reciprocal relationship is sometimes called an electric-magnetic duality. Of course, the name is intended metaphorically.
SO(k, l), where "l" is lower case L, is the non-compact form of SO(k + l) that preserves a metric with k plus signs, and l minus signs. The group SO(k) x SO(l) is its maximal compact subgroup. The quotient space SO(k, l)/SO(k) x SO(l) is a homogenous space of dimension kl. The discrete group SO(k, l; Z) is an infinite group consisting of all SO(k, l) matrices with integer entries. When l = k + 16, it is the subgroup of SO(k, l) that preserves a certain even self-dual lattice of signature (k, l) introduced by Narian. The Narian space Mk, l is defined as
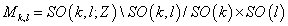
Mk, l = SO(k, l; Z) \ SO(k, l) / SO(k) x SO(l)
With the toroidial compactification of the heterotic string, no supersymmetry is broken, and in four dimensions, there are 132 scalar fields on the Narian moduli space M6, 22. The T-duality group for the 4d heterotic string is GT = SO(6, 22; Z). The 132 scalar fields belong to 22 abelian N = 4 gauge multiplets. When you compactify the extra dimensions, 21 of the scalar fields are from the metric, 15 are from the 2-form Buv, and 96 are from the 16 U(1) gauge fields that form the Cartan subalgebra E8 x E8 or SO(32).
The toroidally compactified heterotic string also has two additional scalar fields, the axion, X, and the dilaton, φ, which are in the N = 4 supergravity multiplet. The dilaton is the 10-dimensional dilaton shifted by a function of the other moduli such that the exponential of its vacuum expectation value gives the 4d coupling constant. The 4d axion is the scalar field that is dual to the 2-form Buv in 4d. The supergravity theory that contains these fields is the same one that was studied by Cremmer, Ferrara, and Scherk. They showed that X and φ parametrize the homogeneous space SL(2, R)/U(1). In the quantum theory, only the discrete S-duality subgroup SL(2, Z) is a symmetry, and the moduli space is
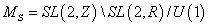
Ms = SL(2, Z) \ SL(2, R) / U(1)
so if you have the following complex scalar field
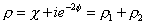
p = X + ie-2[phi] = p1 + p2
where sometimes the 2 is there as a convention, and the vacuum expectation value is
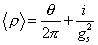
p = [theta]/2[pi] + i/gs2
where θ is the vacuum angle, and gs is the coupling constant, N = 4 Yang-Mills theories have vanishing beta function, so that θ and gs are well defined independent of scale.
In terms of p, the SL(2, Z) symmetry is realized by non-linear transformations.
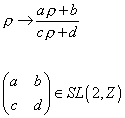
p -> (ap + b)/(cp + d)
When instanton effects are taken into account, the continuous Peccei-Quinn symmetry X → X + b is broken to the discrete subgroup for which b is an integer. This subgroup and the inversion p -> -1/p generate the discrete group SL(2, Z), or when matrices are not distinguished by their negatives, PSL(2, Z). When θ = 0, you have gs = 1/gs. The SL(2, Z) symmetry of the theory is broken completely by any specific choice of vacuum. Only when the vacuum expectation value of p is at one of the orbifold points in the moduli space, does some unbroken symmetry, Z2 or Z3, remain.
The Type IIA and IIB superstring theory compactification on T6 is approximated at low energy by N = 8 supersymmetry. The classical theory has a non-compact symmetry group E7, 7. The duality group is the discrete subgroup E7(Z), which is the intersection of the continuous E7, 7 group and the discrete group Sp(28; Z). In the 56-dimensional fundamental representation, E7, 7 is a subgroup of the non-compact group Sp(28). The Narian moduli space is
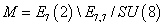
M = E7(Z) \ E7, 7 / SU(8)
Let's say you have supersymmetry with N > 1. The extended 4d supersymmetry algebra in 2-component notation includes the anticommutator
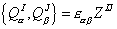
{Q[alpha]I, Q[beta]J} = [epsilon][alpha][beta]ZIJ
The central charges are where ZIJ = -ZJI, and the number of central charges is
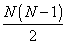
N(N - 1)/2
where N is the number of the supersymmetry. The central charges are complex numbers whose real and imaginary parts give the electric and magnetic charges associated with the N(N - 1)/2 U(1) gauge fields in the N-extended 4d supergravity multiplet. Therefore, the supersymmetry algebra causes the mass of any state to be bounded below by its central charges. This lower bound is called the Bogomol'nyi bound. When the mass of a state reaches the minimum value allowed for the given charges and moduli, the state is called BPS saturated. BPS states belong to smaller representations of the algebra then are possible when the bound is not saturated. These states are often called BPS branes, named after Bogomol'nyi, Prasad, and Sommerfield.
Let's look at the N = 4 supersymmetry. You have
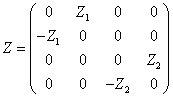
In the N = 4 case, even though the supergravity multiplet has six U(1) gauge fields, you can describe a generic configuration by only describing two electric and two magnetic states. There are two ways to achieve BPS saturation. In the first way, the mass satisfies the following relation
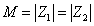
M = | Z1 | = | Z2 |
This gives ultrashort multiplets, such as the 16-dimensional gauge multiplet. The second way to create a BPS state is if you have
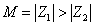
M = | Z1 | > | Z2 |
The first scenario takes place when the electric charge vector αa and the magnetic charge vector βa are parallel. The second scenario takes place when they are not parallel. Since the BPS states in the perturbative string spectrum are purely electric, they are therefore of the first type.
This actually allows you to make comparisons between string states and black holes. Static extremal black hole configurations with
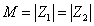
M = | Z1 | = | Z2 |
turn out to preserve one half of the supersymmetry, and have a horizon of vanishing area, and thus no Berkenstein-Hawking radiation. Static extremal black hole configurations with
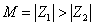
M = | Z1 | > | Z2 |
preserve only one fourth of the supersymmetry, and have a horizon of finite area. Let's say you have N = 8 supersymmetry. In that case, in order to obtain a finite area horizon, M would have to be equal to only one of the four | Zi |'s, so that 7/8 of the supersymmetry is broken, and only 1/8 is preserved. This allows you to measure the entropy of supersymmetric black holes with finite area horizons by counting the number of microscopic string degrees of freedom.
Let's look at M-theory in more detail. In 1978, Cremmer, Julia, and Scherk developed 11-dimensional supergravity which was non-renormalizable and did not admit compactifications. It turned out that Type IIA superstring theory is the dimensional reduction of d = 11 supergravity. The 2-form potential of d = 10 supergravity is associated with a string. The 3-form potential of d = 11 supergravity is associated with a membrane. While it was known how to incorporate spacetime supersymmetry into string theory using the Green-Schwarz world sheet action, it was not known how to generalize this to higher dimensional objects. They were able to solve this problem by looking at d = 4 theories that were actually dimensional reductions from higher dimensional theories. It was known that the d = 4 Green-Schwarz action could be interpreted as the effective action for Nielson-Olesen vortices in a N = 2 supersymmetric abelian Higgs model, which is actually a dimensional reduction to d = 4 from d = 6, and where the vortices are what we would now call D3-branes. The effective action for this d = 4 D3-brane is a higher dimensional generalization of the Green-Schwarz action, which is exactly what we were looking for. This pointed the way to a construction by E. Bergshoeff, E. Sezgin, and P. K. Townsend in 1988, of a d = 11 supermembrane action, and the interpretation of d = 11 supergravity as the effective field theory of a hypothetical supermembrane theory. It was later showed that the Green-Schwarz action for the Type IIA superstring is the dimensional reduction of the d = 11 supermembrane action. This suggested an interpretation of the Type IIA superstring as a membrane wrapped around the 11th dimension which had been compactified on a circle. In 1994, M. J. Duff, K. S. Stelle, G. W. Gibbons, and P. K. Townsend constructed an extreme membrane solution of d = 11 supergravity, and showed that it reduces in d = 10 to the extreme string solution of type IIA supergravity, which had been earlier identified as the field theory realization of the Type IIA string.
Now at this point, the connections between d = 10 and d = 11 physics were still classical. It still seemed unrealistic that the quantum IIA superstring theory, with d = 10 as its critical dimension, could be 11-dimensional. In addition, the non-renormalizability of d = 11 supergravity appeared to have been simply replaced by the difficulty of a continuous spectrum for the first quantized supermembrane. However, the inclusion of wrapping modes of the membrane and 5-brane led to a spectrum of solitons identical to that of the IIA string if the latter includes the wrapping modes of the d = 10 p-branes carrying Ramond-Ramond charges. However, if this is to be taken to mean that IIA superstring theory really is 11-dimensional, then its non-perturbative spectrum in d = 10 must include the Kaluza-Klein excitations from d = 11. These would have long range 10-dimensional fields, and so would have to appear as BPS-saturated 0-brane solutions of IIA supergravity. Such solutions, and their 6-brane duals, were already known to exist, and they were then interpreted as field realizations of the Kaluza-Klein modes, and the Kaluza-Klein 6-branes needed for the d = 11 interpretation of Type IIA superstring theory.
Because of the connection between the string coupling constant and the dilaton, it was obvious that you needed a better understanding of the dilaton in order to formulate a non-perturbative string theory. The fact that type IIA supergravity is the dimensional reduction of d = 11 supergravity, leads to an interpretation of the dilaton as a measure of the radius of the circle that the 11th dimension is compactified on. This leads to the following relation.
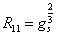
R11 = gs2/3
where R11 is the radius of the circle that the 11th dimension of M-theory is compactified on.
This shows that a power series in gs is an expansion about R11 = 0, so that the 11th dimension would go to zero radius, and not be detectable in string perturbation theory. This connection between the string coupling constant and the radius of the compactified 11th dimension could have been used earlier if people had thought of it. The reason they did not is because the area of the wrapped brane, and thus its energy, is proportional to R11. This implied that the tension of the membrane would vanish in the R11 → 0 limit. The reason this does not happen is because the energy as measured in d = 10 superstring theory differs from that measured in d = 11 by a factor of R11, which is such as to ensure that the d = 10 string tension is independent of R11, and therefore non-zero in the R11 → 0 limit. This also ensures that the 0-brane mass is proportional to 1/R11, which you need for its interpretation as a Kaluza-Klein excitation. In the strong coupling limit, R11 goes to infinity, the vacuum is 11-dimensional Minkowski, and the effective field theory is 11-dimesional supergravity.
Let's look at how you get a chiral theory like Type IIB superstring theory from a compactification of M-theory. This is a specific example of the general problem of how do you get chiral theories from compactifying d = 11 supergravity. There are two ways to do this. The first way uses the fact that you can consider compactifications of M-theory on orbifolds. The second way, which is what's used for Type IIB string theory, is that chiral theories can emerge as limits of non-chiral theories as a result of massive modes not present in the Kaluza-Klein spectrum. Let's say you have d = 11 supergravity compactified on T2. You have d = 9 N = 2 supergravity coupled to a KK tower of massive spin-2 multiplets. In the limit where the surface area of the torus goes to zero, keeping the shape the same, you get the non-chiral d = 9 supergravity theory. If you have M-theory compactified on T2, you also have massive spin-2 multiplets coming from membrane wrapping modes on T2. Those additional massive modes become massless in the limit of the area of the torus going to zero, in such a way so that the effective theory of resulting massless fields is the 10-dimensional chiral Type IIB supergravity. Since this is a chiral theory, there are two versions of it, either right-handed or left-handed. Which one you get depends on the sign of the Chern-Simons term in the d = 11 supergravity Lagrangian, or on the sign of the Wess-Zumino term in the supermembrane action. Therefore, M-theory includes a mechanism that allows for the emergence of chirality upon compactification.
A torus has two radii. Let's say one is the radius of the 10th dimension, R10, and the other radius of the torus is the radius of the 11th dimension, R11, so the 10th and 11th spacetime dimensions are compactified on a torus.
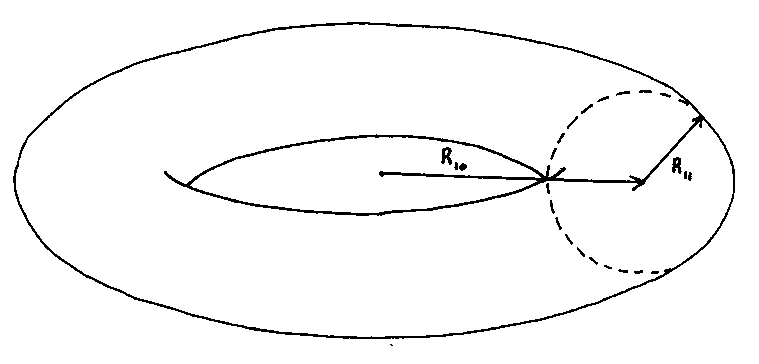
If you look at the limit
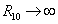
R10 -> [infinity]
at fixed R11, you end up with Type IIA theory, with coupling constant
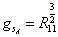
gsA = R113/2
where gsA is coupling constant of Type IIA superstring theory. Now, remember that Type IIA and Type IIB superstring theory are T duals. Type IIA theory is equivalent to Type IIB theory compactified on a circle of radius 1/R10. It follows that the S1-compactified IIB theory can be understood as T2-compactified M-theory. If you look at the limit
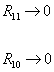
R11 -> 0
R10 -> 0
at fixed ratio, you end up with uncompactified IIB theory with string coupling constant
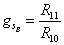
gsB = R11/R10
where gsB is the coupling constant of IIB theory.
The interchange of R10 and R11 is simply a reparametrization of the torus. In other words, the IIB theory at coupling gsB is equivalent to IIB theory at coupling 1/gsB. More generally, the discrete SL(2, Z) group of global reparametrizations of the torus implies an SL(2, R) symmetry of the IIB theory, originally proposed on the basis of the SL(2, R) symmetry of IIB supergravity. The following diagram of moduli space shows how Type IIA, Type IIB, and M-theory are related through T2 compactification.
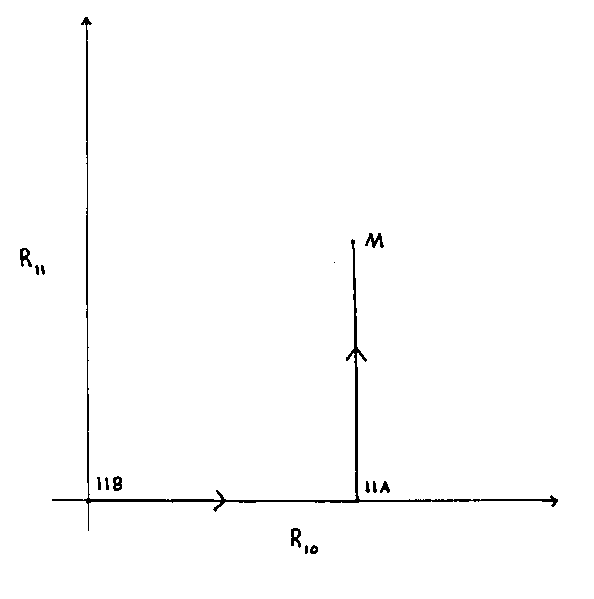
So if you start with Type IIB theory, and increase R10, you end up with Type IIA theory. Then if you have Type IIA theory, and increase R11, you end up with M-theory. A generic point on this diagram refers to an 11-dimensional vacuum. If R11 = 0, and R10 → 0, you have free string theories. (R10, R11) = (0, 0) corresponds to the uncompactified IIB superstring theory for which the vacuum is 10-dimensional Minkowski spacetime. (R10, R11) = (0, 0) is not really a point in the moduli space because the IIB coupling constant depends on how the (R10, R11) → (0, 0) limit is taken. The Type IIA theory has a straightforward interpretation as M-theory compactification.
The S1 compactified IIB theory belongs to the same moduli space as the T2-compactified M-theory. How does the d = 11 membrane emerge from IIB theory? The Type IIB theory is not just a theory of strings, but also contains M3-branes. If during S1-compactification, the M3-brane wraps around the circle, it becomes an M-theory membrane. However, what if it does not wrap around the circle? You then have to find this M3-brane in M-theory. The uncompactified M-theory is not just a theory of membranes, but also includes M5-branes. If upon T2-compactification, an M5-brane wraps around the torus, it appears as an M3-brane. Of course, the M5-brane could also not wrap around the torus. You then end up with both M3-branes and M5-branes in all the different compactifications. Here we are using Mp-brane to mean a Dp-brane within the spectrum of M-theory, and using membrane to mean a D2-brane.
From the description of IIB superstring theory as a limit of a T2-compactified M-theory, the complex structure of the torus, viewed as a Riemann surface, will survive the limit to become a parameter determining the choice of IIB vacuum. This parameter is the vacuum value of the complex IIB supergravity field
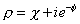
p = X + ie-[theta]
where φ is the dilaton, and X is the axion. If p were assumed to be single-valued in the upper half plane, then it would have to be constant over the complex KK space in any compactification of the IIB theory.
However, p actually takes values in the fundamental domain of the modular group of the torus, so it doesn't have to be single-valued in the upper half plane. A class of compactifications that takes advantage of this possibility is called F-theory.
F-theory is a hypothetical 12-dimensional theory. 11d supergravity, and thus M-theory, can be compactified on a Ricci-flat four dimensional K3 manifold. For some Ricci-flat metrics, K3 can be viewed as an elliptic fibration of CP1, meaning as a fiber bundle where the fiber is a torus whose complex structure p varies over a Riemann sphere. Generically, there will be 24 singular points on the Riemann sphere at which the torus degenerates, but these are merely coordinate singularities as long as no two singular points are in the same place. Thus, there exists M-theory compactifications on manifolds that are locally isomorphic to T2 x S2. If the 2-torus is then shrunk to zero area, you get an S2 compactification of the IIB theory in which the scalar field p varies over S2. More generally, given a Ricci-flat manifold E that is an elliptic fibration of a compact manifold B, you can define F-theory on E as IIB theory on B with p varying over B in a way proscribed by its identification as the complex structure of the torus in the description of E as an elliptic fibration. F-theory would then be a 12-dimensional theory.
Let's now look at the two heterotic string theories. The two heterotic strings have d = 10 N = 1 supersymmetry, and are related to each other by T-duality, at least to all orders in perturbation theory. The compactification of either theory on a circle allows a non-vanishing Wilson line, the integral of A, around the circle, where A is the Lie algebra valued gauge field of the effective supergravity and Yang-Mills theory. You are essentially choosing a non-zero expectation value for the component A in the compact direction. The expectation value must lie in the Cartan subalgebra of either SO(32) or E8 x E8. The gauge group is broken to SO(16) x SO(16). A SO(16) x SO(16) heterotic string theory obtained by compactification of the SO(32) heterotic string on a circle of radius R can also be obtained by compactification of the E8 x E8 theory on a circle of radius 1/R. Therefore, the uncompactified SO(32) and E8 x E8 heterotic string theories are theories with vacua that are limiting points in a single connected space of vacua. SO(32) and E8 x E8 heterotic strings are related by T-duality. SO(32) heterotic and Type I string theories are related by S-duality. It turns out that Type I string theory can be derived from Type IIB string theory.
Let's look at Type I string theory. Type I string theory is an orientifold of Type IIB theory. The Type IIB string action is invariant under a world sheet parity operation called Ω which exchanges left-movers and right-movers. You can therefore find a new string theory by gauging this symmetry. This projects out the world sheet parity odd states of the Type IIB superstring theory, leaving the states of the closed string sector of Type I theory. This sector is anomalous by itself but you can add an open string sector which can be viewed as an analog of the twisted sector in more conventional orbifold construction. An anomaly free theory can then be obtained by including SO(32) Chan-Paton factors at the ends of the open strings. This is Type I string theory. From its origin in IIB theory, it is obvious that the S1-compactified Type I string must be 11-dimensional. Since the IIA theory has a more direct connection to d = 11 then IIB, and IIA is the T-dual of IIB, it is logical to expect that the connection between Type I and d = 11 will be more obvious if you consider its T-dual. The T-dual of Type I string theory is called Type IA or Type I' theory.