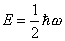
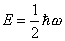
E = (1/2)[h bar]w
and the fermionic part gives
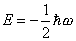
E = - (1/2)[h bar]w
and so they cancel each other out exactly. Therefore, if supersymmetry were unbroken, you would have zero vacuum energy. Even though it's not unbroken at low energies, they cancel out at high energies where supersymmetry is unbroken. Therefore, above the supersymmetry breaking scale, the bosonic and fermionic contributions to the Higgs mass cancel out. Supersymmetry adds fermionic contributions along with the bosonic contributions to the self-energy of the Higgs mass to solve the hierarchy problem.
The fermionic and bosonic contributions to the vacuum energy also cancel out. If there was an unbroken supersymmetry, we would have no vacuum energy, although obviously we don’t have an unbroken supersymmetry. However, the fermionic and bosonic contributions to the vacuum energy will cancel out above the supersymmetry breaking scale. Therefore, supersymmetric models predict a vacuum energy only 1055 times larger than the observed value, instead of 10120 times larger.
Therefore, what supersymmetry ultimately boils down to is including anticommutators along with commutators. A symmetry of the S-matrix means that symmetry transformations have the effects of merely reshuffling the asymptotic single and multiparticle states. The Coleman-Mandula theorem, postulated by Sidney Coleman and Jeffrey Mandula in 1967, states that the only symmetries of the S-matrix are the following.
1. Poincare invariance, which is the semi-direct product of translated and Lorentz rotations, with generators Pm and Mmn.
2. Internal global symmetries, related to conserved quantum numbers, such as electric charge and isospin. The symmetry generators are Lorentz scalars, and generate a Lie algebra.
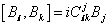
[Bl, Bk] = iClkj Bj
where Clkj are structure constants.
3. Discrete symmetries, which are C, P, and T.
In 1975, Haag, Lopuszanski, and Sohnius proved that by weakening the assumptions of the Coleman-Mandula theorem, you end up with supersymmetry. Specifically, they weakened the assumption that the symmetry algebra of the S-matrix involves only commutators. If you allow both commutating and anticommutating generators, you end up with supersymmetry. Supersymmetry is the introduction of anticommuting symmetry generators which transform as the ( ½, 0) and (0, ½) spinor representations of the Lorentz group. Since these new symmetry generators are spinors, not scalars, supersymmetry is not an internal symmetry. Rather, it is an extension of the Poincare symmetry by anticommuting spinor generators.
The new symmetry we are looking for must connect bosons and fermions. In other words, the generators Q of this symmetry must turn a bosonic state into a fermionic state, and vice versa. This in turn implies that the generators themselves carry half-integer spin, and are thus fermionic. This is in contrast to the generators of the Lorentz group, or with gauge group generators, which are all bosonic. The simplest choice of SUSY generators is a 2-component Weyl spinor Q, and its conjugate [Q bar]. Since the generators are fermionic, their algebra can be most easily written in terms of anticommutators.
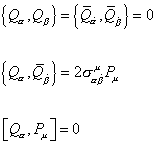
{Q[alpha], Q[beta]} = {[Q bar][alpha dot], [Q bar][beta dot]} = 0
{Q[alpha], [Q bar][beta dot]} = 2[sigma][alpha] [beta dot]u Pu
[Q[alpha], Pu] = 0
where α and β of Q, and [α dot] and [β dot] of [Q bar] take values 1 or 2. σu = (1, σi) where σi are the Pauli spin matrices. Pu is the translation generator. For a compact description of SUSY transformations, we introduce fermionic coordinates θ and [θ bar]. These are anticommuting Grassmann variables.
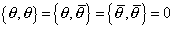
{[theta], [theta]} = {[theta], [theta bar]} = {[theta bar], [theta bar]} = 0
A finite SUSY transformation can be written as
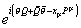
ei([theta]Q + [Q bar] [theta bar] - xu Pu)
compared to a non-abelian gauge transformation
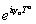
ei[psi]a Ta
where Ta is the group generators.
The objects on which SUSY transformations acts on must also depend on θ and [θ bar]. You therefore need superfields which are functions of θ and [θ bar] as well as the spacetime coordinates xu. Since θ and [θ bar] are two component spinors, you could even say that supersymmetry doubles the dimensions of spacetime, the new dimensions being fermionic. Poincare transformations are transformations from one reference frame to another, and supersymmetry is an extension of that, so you could think of it as movement into some sort of superspace within which bosons and fermions exchange identities. I should emphasize that very few people think of supersymmetry in that way. Most people tend to think of it more like a discrete symmetry, such as turning a particle into its antiparticle, although mathematically it's not. Thus, you have a discrepancy between how supersymmetry transformations are handled mathematically, and how they are handled psychologically.
For most practical purposes, it's sufficient to consider infinitesimal SUSY transformations which are written as
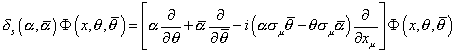
[delta]s([alpha], [alpha bar]) [capital phi] (x, [theta], [theta bar]) = [[alpha] [partial derivative with respect to theta] + [alpha bar] [partial derivative with respect to theta bar] - i([alpha] [sigma]u [theta bar] - [theta] [sigma]u [alpha bar]) [partial derivative with respect to xu]] [capital phi] (x, [theta], [theta bar])
where Φ is a superfield, and α and [α bar] are Grassmann variables. This corresponds to the following explicit representation of the SUSY generators.
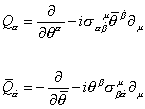
Q[alpha] = [partial derivative with respect to [theta][alpha]] -i[sigma][alpha] [beta dot]u [theta bar][beta dot] [partial derivative with respect to u]
[Q bar][alpha dot] = -[partial derivative with respect to [theta bar][alpha dot]] + i[theta][beta] [sigma][beta] [alpha dot]u [partial derivative]u
The following are the SUSY-covariant derivatives which anticommute with the SUSY transformations.
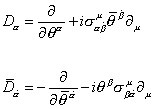
D[alpha] = [partial derivative with respect to [theta][alpha]] + i[sigma][alpha] [beta dot]u [theta bar][beta dot] [partial derivative with respect to u]
[D bar][alpha dot] = -[partial derivative with respect to [theta bar][alpha dot]] - i[theta][beta] [sigma][beta] [alpha dot]u [partial derivative]u
The above equations have been written in such a way as to treat θ and [θ bar] the same. It's often convenient to use chiral representation where θ and [θ bar] are treated slightly differently.
Left-handed or L-representation
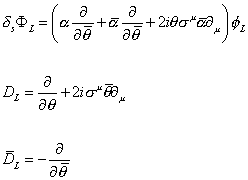
[delta]s [phi]L = ([alpha] [partial derivative with respect to [theta bar]] + [alpha bar] [partial derivative with respect to [theta bar]] + 2i[theta] [sigma]u [alpha bar] [partial derivative]u) [capital phi]L
DL = [partial derivative with respect to [theta]] + 2i[sigma]u [theta bar] [partial derivative]u
[D bar]L = -[partial derivative with respect to [theta bar]]
Right-handed or R-representation
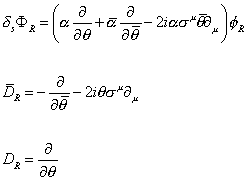
[delta]s [capital phi]R = ([alpha] [partial derivative with respect to [phi]] + [alpha bar] [partial derivative [theta bar]] - 2i[alpha] [sigma]u [theta bar] [partial derivative]u) [capital phi]R
[D bar]R = -[partial derivative with respect to [theta bar]] - 2i[theta] [sigma]u [partial derivative]u
DR = [partial derivative with respect to [theta]]
Notice that [D bar] has a particularly simple form in the L-representation, and D has a particularly simple form in the R-representation. Normally, you choose the representation that would most simplify the notation. However, you have to stick with whichever representation you're using, so you don't always have the luxury of writing a given quantity in the representation that would give it the simplest form. The following identity allows you to go back and forth between representations.
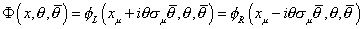
[capital phi] (x, [theta], [theta bar]) = [phi]L (xu + i[theta] [sigma]u [theta bar], [theta], [theta bar]) = [phi]R (xu -i[theta] [sigma]u [theta bar], [theta], [theta bar])
So far, everything has been written for arbitrary superfields. However, at this point, you need to specify two special kinds of superfields called irreducible superfields. The two kinds of irreducible superfields are called chiral superfields and vector superfields.
The first type of superfield is the chiral superfield. The Standard Model fermions are chiral. Their left-handed and right-handed forms transform differently under SU(2) x U(1). This is another way of saying the weak force is parity violating. Therefore, you need superfields with two fermionic degrees of freedom, which can then describe the left-handed and right-handed components of the Standard Model fermions. Of course, the same superfields also contain bosonic partners, the sfermions. Therefore, you require either
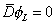
[D bar] [phi]L = 0
where φL is left chiral, or
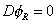
D [phi]R = 0
where φR is right chiral. Notice that these are very simply expressed using the chiral representation of SUSY generators, or SUSY-covariant derivatives. For instance, the L-representation, φL, is independent of [θ bar]. Remembering that θ is an anticommuting Grassmann variable, you can expand φL as
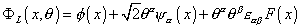
[capital phi]L (x, [theta]) = [phi](x) + [square root of 2] [theta][alpha] [psi][alpha](x) + [theta][alpha] [theta][beta] [epsilon][alpha] [beta] F(x)
where summation over identical indices is assumed, and εα β is the Levi-Civita tensor. F is a scalar field. φ has dimensions of mass. θ has dimensions of mass-½. The fermionic field has dimensions of m-3/2. The superfield φ has dimensions of mass. So far, this is what you would expect. However, in order to be dimensionally consistent, the field F would have to have the unusual dimensions of m2, which is hard to interpret. If something has dimensions of massn, or mn, you say it has mass dimension n. Another problem is that ΦL seems to contain four bosonic degrees of freedom, and only two fermionic degrees of freedom, so they do not cancel.
However, these two puzzles in fact solve each other. The fact F has dimensions of m2 means that a free kinetic term for F would be dimensionally inconsistent, which means it's not a propagating field. Therefore, not at all of the bosonic fields represent physical propagating degrees of freedom. Therefore, there are equal numbers of propagating bosonic and fermionic degrees of freedom. As it turns out, F, and another field I'll mention later called D, are auxiliary fields that have to be introduced partly because a fermion has more degrees of freedom than a boson. They are eventually eliminated. You could think of them purely as a book keeping device. You could also think of them as particles that exist only as internal lines in Feynman diagrams, and never appear in external lines. For instance, if you have a quadralinear Higgs vertex, meaning four Higgs lines meeting at a single vertex, you could imagine it as two trilinear Higgs vertices, where two Higgs particles exchange an F particle.
The result for φR in R-representation is the same as that for φL in L-representation, replacing θ with [θ bar]. You could, of course, write a left-handed superfield using right-chiral representation of the SUSY generators, or vice versa. It's just that the resulting equation is much longer and more complicated.
Applying the L-representation of the SUSY transformation to the left-chiral superfield gives
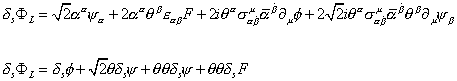
[delta]s [capital phi]L = [square root of 2] [alpha][alpha] [psi][alpha] + 2[alpha][alpha] [theta][beta] [epsilon][alpha] [beta] F + 2i[theta][alpha] [sigma]u[alpha] [beta dot] [alpha bar][beta dot [partial derivative]u [phi] + 2[square root of 2] i[theta][alpha] [sigma]u[alpha] [beta dot] [alpha bar][beta dot] [theta][beta] [partial derivative]u [psi][beta]
[delta]s [capital phi]L = [delta]s [phi] + [square root of 2] [theta] [delta]s [psi] + [theta] [theta] [delta]s F
Just to remind you again what the variables are, the SUSY generators are Q, the indices of which are α and β, and [Q bar], the indices of which are [α dot] and [β dot]. θ and [θ bar] are the fermionic coordinates, and are Grassmann variables with dimensions of m-½. φ is the scalar field, and has dimensions of m. Φ is the superfield, and has dimensions of m. ψ is the Weyl spinor, and is a fermionic field with dimensions m3/2. σu = (1, σi), where σi is the Pauli spin matrices. δs is the SUSY transformation. F is the auxiliary field with dimensions m2. εα β is the Levi-Civita tensor.
Now, the first two terms in the above equation come from the
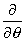
[partial derivative with respect to [theta]]
part of δs while the last two terms come from the
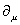
[partial derivative]u
part. The ∂u applied to the last term in the equation for ΦL vanishes. The second line in the above equation just says that the SUSY algebra should close, meaning the SUSY transformation applied to a left-handed chiral superfield should give a left-chiral superfield. Finally, the SUSY transformation has the following effect on the following terms.
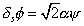
[delta]s [phi] = [square root of 2] [alpha] [psi]
which converts bosons to fermions
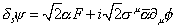
[delta]s [psi] = [square root of 2] [alpha] F = i[square root of 2] [sigma]u [alpha bar] [partial derivative]u [phi]
which converts fermions to bosons
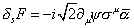
[delta]s F = -i[square root of 2] [partial derivative]u [psi] [sigma]u [alpha bar]
The chiral superfields can describe spin-0 bosons, which in the Standard Model is just the Higgs boson, as well as spin-½ particles, which are the quarks and leptons of the Standard Model. However, they do not describe the spin-1 gauge bosons of the Standard Model. In order to describe spin-1 particles, the vector bosons, you need to introduce vector superfields. They are constrained to be self-conjugate.
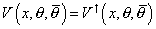
V(X, [theta], [theta bar) = V† (X, [theta], [theta bar])
This leads to the following representation of V.
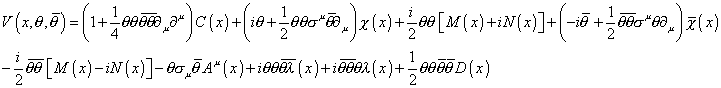
V(X, [theta], [theta bar]) = (1 + (1/4) [theta] [theta] [theta bar] [theta bar] [partial derivative]u [partial derivative]u) C(x) + (i[theta] + (1/2) [theta] [theta] [sigma]u [theta bar] [partial derivative]u) X(x) + (i/2) [theta] [theta] [M(x) + iN(x)] + (i[theta bar] + (1/2) [theta bar] [theta bar] [sigma]u [theta] [partial derivative]u) [X bar] (x) - i/2 [theta bar] [theta bar] {M(x) - iN(x)] - [theta] [sigma]u [theta bar] Au (x) + i[theta] [theta] [theta bar] [lambda bar] (x) - i[theta bar] [theta bar] [theta] [lambda](x) + (1/2) [theta] [theta] [theta bar] [theta bar] D(x)
where C, M, N, and D are real scalars, X and λ are Weyl spinors, and Au is a vector field. If Au is to describe a gauge boson, V must transform as the adjoint representation of the gauge group.
Obviously, the above equation is very unwieldy, but fortunately, you now have many more gauge degrees of freedom than in non-supersymmetric theories, since now, the gauge parameters are themselves superfields. A general non-abelian supersymmetry acting on V can be described as
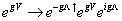
egV -> e-eg[capital lambda] † egV eig[capital lambda]
where
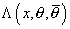
[capital lambda] (x, [theta], [theta bar])
is a chiral superfield, and g is the gauge coupling.
In the case of an abelian gauge symmetry, this transformation rule can be written as
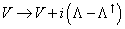
V -> V + i([capital lambda] - [capital lambda]†)
Remember that a chiral superfield contains four scalar bosonic degrees of freedom as well as one Weyl spinor. Therefore, you can use the above transformations to choose
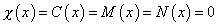
X(x) = C(x) = M(x) = N(x) = 0
greatly simplifying the above equation. This is called the Wess-Zumino gauge, or the W-Z gauge. It is the SUSY analog of the unitary gauge in ordinary quantum field theory since it removes any unphysical degrees of freedom. Notice that we have used only three of the four bosonic degrees of freedom in Λ. You therefore still have the ordinary gauge freedom
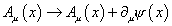
Au(x) -> Au(x) + [partial derivative]u [psi](x)
for an abelian theory. Therefore, the W-Z gauge can be used in combination with any of the usual gauges. However, the W-Z gauge is sufficient to greatly simplify the expression for V, removing the first five terms, leaving only the last four.
If Au has dimensions of mass, and the fermionic field has dimensions of m3/2, that gives D the unusual dimensions of m2, same as the F-component of the chiral superfield.
Applying the SUSY transformations gives a much longer expression than in the chiral superfield case so I'll just give the following result.
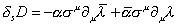
[delta]sD = -[alpha] [sigma]u [partial derivative]u [lambda bar] + [alpha bar] [sigma]u [partial derivative]u [lambda]
which shows that the D-component of a vector field transforms into a total derivative, same as the F-component of a chiral superfield.
Now let's try to write down the supersymmetry Lagrangian. You want the action to be invariant under SUSY transformations.
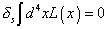
[delta]s [integral] d4 x L(x) = 0
This is satisfied if L itself transforms into a total derivative. The highest components, meaning those with the largest number of θ and [θ bar] factors, of chiral and vector superfields satisfy this requirement, so you can use them to construct the Langrangian. Let's write the action as
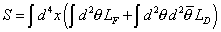
S = [integral] d4x ([integral] d2 [theta] LF + [integral] d2 [theta] d2 [theta bar] LD)
where integration over Grassmann variables is defined as
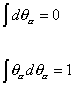
[integral] d[theta][alpha] = 0
[integral] [theta][alpha] d[theta][alpha] = 1
with no summation over α. LF and LD are general chiral and vector superfields, giving rise to F-terms and D-terms respectively.
Let's compute the product of two left-chiral superfields.
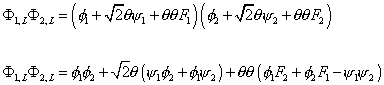
[capital phi]1, L [capital phi]2, L = ([phi]1 + [square root of 2] [theta] [psi]1 + [theta] [theta] F1) + ([phi]2 + [square root of 2] [theta] [psi]2 + [theta] [theta] F2)
[capital phi]1, L [capital phi]2, L = [phi]1 [phi]2 + [square root of 2] [theta] ([psi]1 [phi]2) + [theta] [theta] ([phi]1 F2 + [phi]2 F1 - [psi]1 [psi]2)
Since this is itself a left-chiral superfield, it does not depend on [θ bar], so it is a candidate for a contribution to the LF term in the action. In fact, the last term looks like a fermion mass term.
If the product of two left-chiral superfields is a left-chiral superfield, the same must be true for the product of any number of left-chiral superfields. Let's compute the highest component in the product of three such fields.
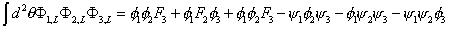
[integral] d2[theta] [capital phi]1, L [capital phi]2, L [capital phi]3, L = [phi]1 [phi]2 F3 + [phi]1 F2 [phi]3 + [phi]1 [phi]2 F3 - [psi]1 [phi]2 [psi]3 - [phi]1 [psi]2 [psi]3 - [psi]1 [psi]2 [phi]3
Notice the last three terms describe Yukawa interactions between one scalar and two fermions. In the Standard Model, such interactions give rise to quark and lepton masses. Therefore, this is an interaction term in the SUSY Lagrangian. Notice that if you call φ1 the Higgs field, ψ2 the left-handed top quark, and ψ3 the left-handed anti-top, the above equation will not only produce the desired Higgs-top-top interaction, but also interactions between a scalar top, called stop, the fermionic higgsino, and the top quark with equal strength. This illustrates how relations between the couplings are enforced by supersymmetry.
So far, we have identified terms that give rise to explicit fermion masses, as well as Yukawa interactions, but not yet found any terms with derivatives that can be identified with kinetic energy terms. Simply multiplying more left-chiral superfields is not going to work since that would give rise to terms with mass dimension > 4, which is nonrenormalizable. Instead, let's consider the product of a left-chiral superfield and its conjugate, which is a right-chiral superfield. You have to be consistent in whether you're using L-representation or R-representation. Since we're doing this calculation in L-representation, that means you have to write the right-chiral superfield in L-representation. This gives
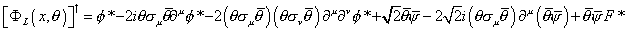
[[phi]L (x, [theta])]† = [phi]* - 2i[theta] [sigma]u [theta bar] - 2([theta] [sigma]u [theta bar]) ([theta] [sigma]v [theta bar]) [partial derivative]u [partial derivative]v [phi]* + [square root of 2] [theta bar] [psi bar] - 2[square root of 2]i ([theta] [sigma]u [theta bar]) [partial derivative]u ([theta bar] [psi bar]) + [theta bar] [theta bar] F*
The product
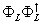
[capital phi]L [capital phi]L†
is self-conjugate, so it can be identified with a vector superfield. It is therefore a candidate for the contribution of the D-terms in the action.
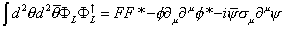
[integral] d2 d2 [theta bar] [capital phi]L [capital phi]L* = FF* - [phi] [partial derivative]u [partial derivative]u [phi]* - i[psi bar] [sigma]u [partial derivative]u [psi]
This contains kinetic energy terms for the scalar component φ as well as the fermionic component ψ of chiral superfields. Notice it does not contain kinetic energy terms for F. Therefore, the F field does not propagate. It is merely an auxiliary field which can be integrated out exactly using its purely algebraic equation of motion. A chiral superfield therefore only has two physical bosonic degrees of freedom, described by the complex scalar φ. It contains equal numbers of propagating bosonic and fermionic degrees of freedom.
In order to remove the F-fields from the Lagrangian, define the superpotential f.
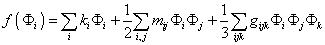
f([capital phi]i) = [summation over i] ki [phi]i + (1/2) [summation over ij] mij [capital phi]i [capital phi]j + (1/3) [summation over i, j, k] gijk [capital phi]i [capital phi]j [capital phi]k
where Φi are all left-chiral superfields, and ki, mij, and gijk are all constants of mass dimension 2, 1, and 0 respectively. The contributions to the Lagrangian that we have mentioned so far can be written as
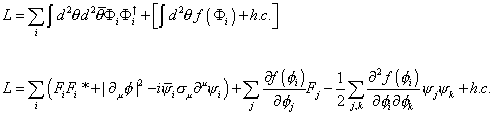
L = [summation over i] [integral] d2 [theta] d2 [theta bar] [capital phi]i [capital phi]i† + [[integral] d2 [theta] f([capital phi]i) + h. c.]
L = [summation over i] (Fi Fi* + | [partial derivative]u [phi] |2 - i[psi bar] [sigma]u [partial derivative]u [psi]i) + [summation over i] [partial derivative of f([phi]i) with respect to [phi]j] Fj - (1/2) [summation over j, k] [second partial derivative of f([phi]i) with respect to [phi]j and [phi]k] [psi]j [psi]k + h. c.
where f is a function of the scalar field φi instead of the superfields Φi. Now integrate out the auxiliary fields. Their equations of motion are given by
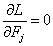
[partial derivative of L with respect to Fj] = 0
which implies
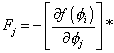
Fj = -[partial derivative of f([phi]i) with respect to [phi]j]*
Plugging this into the above equation for the Lagrangian gives
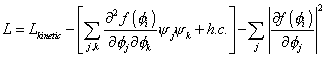
L = Lkinetic - [[summation over j, k] [second partial derivative of f([phi]i) with respect to [phi]j and [phi]k] [psi]j [psi]k + h. c.] - [summation over j] | ] [partial derivative of f([phi]i) with respect to [phi]j] |2
The second term in the Lagrangian describes fermion masses and Yukawa interactions. The third term in the Lagrangian describes scalar mass terms and scalar interactions. Since both terms are determined by a single function f, there are many relations between the coupling constants.
The coupling of the gauge superfields to the chiral matter superfields is done by a SUSY version of the normal minimal coupling.
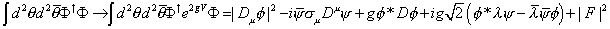
[integral] d2 [theta] d2 [theta bar] [capital phi] † [capital phi] -> [integral] d2 d2 [theta bar] [capital phi]† e2gV [phi] = | Du [phi] |2 - i[psi bar] [sigma]u Du [psi] + g[phi]* D[phi] + ig[square root of 2] ([phi]* - [lambda] [psi] - [lambda bar] [psi bar] [phi]) + | F |2
using the W-Z gauge and the normal gauge covariant derivative
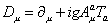
Du = [partial derivative]u + igAua Ta
where Ta are the group generators. This part of the Lagrangian describes not only the interactions of fermions and scalars with gauge fields but also contains gauge strength interactions between fermions or higginos, ψ, Higgs bosons or sfermions, φ, and gauginos, λ. Gauginos are the supersymmetric partners of the gauge bosons.