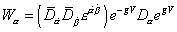
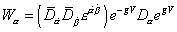
W[alpha] = ([D bar][alpha dot] [D bar][beta dot] [epsilon][alpha dot] [beta dot]) e-gV D[alpha] egV
where D and [D bar] are SUSY-covariant derivatives carrying spinor superscripts. For abelian symmetries, this reduces to
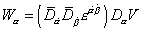
W[alpha] = ([D bar][alpha dot] [D bar][beta dot] [epsilon][alpha dot] [beta dot]) D[alpha] V
since
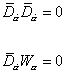
[D bar][alpha dot] [D bar][alpha dot] = 0
[D bar][alpha dot] W[alpha] = 0
Wα is a left-chiral superfield. Its behavior under gauge transformations is the same as egV. The product Wα Wα is gauge invariant. It is also a left-chiral superfield, so its θ θ can appear in the Lagrangian.
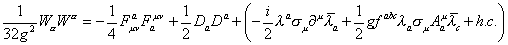
(1/32g2) W[alpha] W[alpha] = -(1/4) Fuva Fauv + (1/2) Da Da + (-(i/2) [lambda]a [sigma]u [partial derivative]u [lambda bar]a + (1/2) gfabc [lambda]a [sigma]u Aau [lambda bar]c + h. c.)
In addition to the kinetic energy term for the gauge fields, there is also a kinetic energy term for the gauginos, as well as the canonical coupling of the gauginos to the gauge fields, determined by the group structure constants fabc. There is no kinetic energy term for the Da fields, so these are also auxiliary fields, and can be integrated out. Their equation of motion is
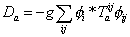
Da = -g[summation of ij] [phi]i* Taij [phi]ij
You also have the following contribution to the scalar interactions in the Lagrangian
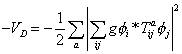
-VD = -½ [summation over a] | [summation over ij] g[phi]i* Tija [phi]j |2
We therefore have all the terms of the Lagrangian of supersymmetry.
If you were to go through the calculations, you would see that there are no quadratic divergences. Obviously, there are no quadratic divergences from Yukawa couplings since each chiral superfield contains equal numbers of bosonic and fermionic degrees of freedom. If you go through the calculations and determine the contributions to the Higgs self-energy due to the gauge bosons, you would see that these also cancel for the same reason. However, if you take into account hypercharge interactions, so you no longer assume that mW = mZ, you will find that a nonvanishing divergence remains. This is because the total trace of the hypercharge generator does not vanish. Its trace over a complete fermion or sfermion generation does vanish, but this leaves the contribution from the single Higgs doublet. The solution to this problem is to have not one but two Higgs doublets.
You need to introduce two Higgs superfields to break SU(2) x U(1). A model with a single Higgs doublet superfield has nonvanishing gauge anomalies associated with fermion triangle diagrams. The contributions from just a Standard Model fermion does vanish, but if you add a single higgsino doublet, anomalies will be introduced. You need a second higgsino doublet with opposite hypercharge to cancel the contribution from the first doublet. Also, the masses of the chiral fermions originate from terms in the superpotential. However, the superpotential can't contain products of left and right chiral superfields. You can't introduce a hermitian conjugate of a Higgs field, so you can't introduce U(1) invariant terms that give mass to both type up and type down quarks, if there is only one Higgs superfield. Therefore, you need at least two doublets.
In the supersymmetry Lagrangian, the masses of the Standard Model particles are exactly the same as their supersymmetric partners. Obviously, this is not the case. We have not yet detected supersymmetric particles so their masses must be much larger than the Standard Model particles. Therefore, supersymmetry must be a broken symmetry. In the Standard Model, SU(2) x U(1) is a spontaneously broken symmetry. However, it's not easy to break supersymmetry spontaneously. From the definition of SUSY algebra
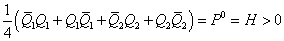
¼ ([Q bar]1 Q1 + Q1 [Q bar]1 + [Q bar]2 Q2 + Q2 [Q bar]2) = P0 = H > 0
where H is the Hamiltonian. This is non-negative since it is the sum of perfect squares. If the vacuum state | 0 > is supersymmetric, then
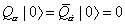
Q[alpha] | 0 > = [Q bar][alpha dot] | 0 > = 0
so therefore
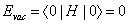
Evac = < 0 | H | 0 > = 0
Let's try breaking supersymmetry by the vacuum expectation value of a scalar particle, in direct analogy with SU(2) x U(1) breaking in the Standard Model. The scalar potential is given by
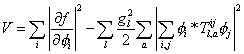
V = [summation over i] | [partial derivative of f with respect to [phi]i] |2 + [summation over l] (gl2/2) [summation over a] | [summation over i, j] [phi]I* Tl, aij [phi]j |2
where l, lower case L, labels the simple groups whose product forms the entire gauge group of the model, such as SU(3) x SU(2) x U(1) in the Standard Model. You can break SUSY with either
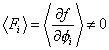
Fi = <[partial derivative of f with respect to [phi]i] is not 0.
which is called F-breaking, or
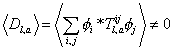
Dl, a = <[summation over i, j] [phi]i* Tl, aij [phi]j> is not 0
which is called D-breaking. The second term in the above equation for V can be minimized, meaning set to zero, if all expectation values vanish.
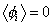
<[phi]i> = 0
for all i. Turning the symmetry breaking point into the absolute minimum of the potential requires nontrivial contributions from the first term in the above equation for V.
The construction of realistic models with spontaneously broken SUSY is made even more difficult by the fact that in such models
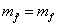
m[f tilda] = mf
still remains satisfied on average, so at least some of the sfermions would still have masses on the order of the Standard Model particles. The supertrace over the whole mass matrix vanishes
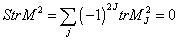
Str M2 = [summation over j] (-1)2J tr M MJ2 = 0
where J is the spin, and MJ is the mass matrix for all particles of spin J. This is a problem since we want all sfermions to be significantly heavier than their Standard Model partners. You can possibly satisfy this constraint by making the gauginos very heavy, but that is also difficult to do in a self-consistent way. All potentially realistic global supersymmetry models of spontaneous SUSY breaking, where sparticles get masses at tree-level, contain a new U(1) whose D-term is nonzero in the minimum of the potential, as well as a large number of superfields beyond those required by the field content of the Standard Model. One way around this is to circumvent the above constraint by instead creating most sparticle masses only through radiative corrections, although this also requires additional superfields.
For this reason, most attempts at SUSY breaking instead do it by inserting soft breaking terms into the Lagrangian. You want to maintain the cancellation of the quadratic divergences. You have to be aware of what terms you can add to the Lagrangian that will still allow the cancellation of quadratic divergences to take place. Quadratic divergences will cancel even if you introduce the following terms.
scalar mass terms
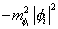
-m[phi]i2 | [phi]i |2
trilinear scalar interactions
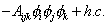
-Aijk [phi]i [phi]j [phi]k + h. c.
gaugino mass terms
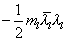
-½ ml [lambda bar]l [lambda]l
bilinear terms
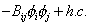
-Bij [phi]i [phi]j + h. c.
and linear terms
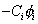
-Ci [phi]i
and under certain conditions, you can add trilinear terms of the form
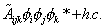
[A tilda]ijk [phi]i [phi]j [phi]k* + h. c.
where l, lower case L, labels the group factor, and h. c. is hermitian conjugate. Linear terms are gauge invariant only for gauge singlet fields. You are not allowed to introduce additional masses for chiral fermions beyond those contained in the superpotential. The relations between dimensionless coupling constants imposed by supersymmetry can't be broken.
Let's now look at the simplest realistic supersymmetric model. This is called the minimal supersymmetric standard model, or MSSM. It is a simple supersymmetrization of the Standard Model. You want to keep the number of superfields and interactions as small as possible. Since the Standard Model fermions are in different representations of the gauge groups than the gauge bosons, we have to place them in different superfields. No Standard Model fermion can be identified as a gaugino. One generation of the Standard Model is therefore described by five chiral superfields. Q contains quark and squark SU(2) doublets. Uc and Dc contain the quark and squark singlets. L contains the lepton and slepton doublets. Ec contains lepton and slepton singlets. The SU(2) singlet superfields contain left-handed and right-handed anti-fermions. Their scalar members have charges of +1 for [e tilda]Rc, -2/3 for [u tilda]Rc, and -1/3 for [d tilda]Rc, where c denotes antiparticles. You repeat everything for each of the three generations.
Let's look at the actual particles. In addition to the gauge bosons, you have spin ½ gaugino fields. The partners to the Bu and Wui are the [B tilda] and [W tilda]i. In the Standard Model, the W1 and W2 combine in one way to create W+, and another way to create W-. The Bu and W3 combine in one way to create the Z0 and another way to create the photon, γ. You have the same thing with the supersymmetric particles. The [W tilda] fields combine in different ways to create the positive and negative winos [W tilda]+ and [W tilda]-. The [B tilda] and [W tilda] combine in one way to create the zino [Z tilda], and another way to create the photino, [gamma tilda]. The superpartners of the eight gluons are the eight gluinos, [g tilda].
Quarks and leptons have spin-0 partners called squarks and sleptons. The partner to the up quark is the up squark. The partner to the electron is the selectron. You could also identify squarks by just putting an "s-" in front of the name of the quark, so the partner to the top would be the stop, etc. Since there has to be a superpartner for each degree of freedom, two bosonic fields are needed for each Standard Model fermion. They are called the left and right states, [q tilda]R, [q tilda]L, [l tilda]R, [l tilda]L.
Lastly, you need two complex Higgs doublets with hypercharges of +1 and -1 in order to give masses to the up-type quarks, down-type quarks, and leptons, and also to cancel anomalies. The Higgs fields have spin-½ partners called higgsinos.
| Superfield | Particle | Spin | Superparticle | Spin |
| V1 | Bu | 1 | 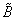 |
1/2 |
| V2 | Wui | 1 | 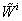 |
1/2 |
| V3 | Gua | 1 | 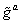 |
1/2 |
| Q | (u, d)L | 1/2 | 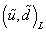 |
0 |
| Uc | 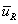 |
1/2 | 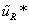 |
0 |
| Dc | 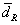 |
1/2 | 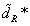 |
0 |
| L | 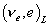 |
1/2 | 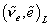 |
0 |
| Ec | 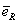 |
1/2 | 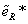 |
0 |
| H1 | (H10, H1-) | 0 | 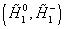 |
1/2 |
| H2 | (H1+, H20) | 0 | 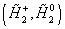 |
1/2 |
Now let's write down the Lagrangian for MSSM. The gauge interactions are determined by the same gauge group as the Standard Model, SU(3) x SU(2) x U(1). Masses and couplings of the matter fields are determined by the superpotential W. The choice of gauge group constrains W but does not fix it completely. Introducing only those terms that are needed to build a consistent model, you have
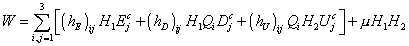
W = [summation of i, j from 1 to 3] ((hE)ij H1 Li Ejc + (hD)ij H1 QI Djc + (hU) Qi H2 Ujc] + uH1 H2
where i and j are generation indices, and we're contracting over SU(2) and SU(3) indices.
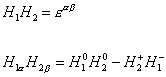
H1 H2 = [epsilon][alpha] [beta]
H1[alpha] H2[beta] = H10 H20 - H2+ H1-
where εα β is the antisymmetric Levi-Civita tensor used to contract over the SU(2)L weak isospin indices α, β = 1. Also
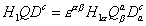
H1 Q Dc = [epsilon][alpha] [beta] H1[alpha] Q[beta]a Dac
where a = 1, 2, 3 are the color indices. The 3 x 3 matrices hD, hU, and hE are dimensionless Yukawa couplings giving rise to quark and lepton masses. Also, hD and hu account for the mixing between quark current eigenstates as described by the KM-matrix. Notice the same superpotential is obtained by requiring that baryon number and lepton number be conserved, which is automatically true in the Standard Model, but not necessarily in MSSM.
You then get the following Lagrangian.
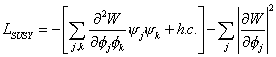
LSUSY = -[[summation over j, k] [second partial derivative of W with respect to [phi]j and [phi]k] [psi]j [psi]k + h. c.] - [summation over j] | [partial derivative of W with respect to [phi]j] |2
where φi are scalar fields, and ψi are fermionic fields. The first term describes masses and Yukawa interactions of fermions. The second term describes scalar terms and scalar interactions.
The interactions obtained in this way respect a symmetry called R-parity, which is defined as R = (-1)L + 3B + 2S, where L is lepton number, B is baryon number, and S is spin. For normal particles, R = 1, and for their supersymmetric partners, R = -1. In confusing terminology, a particle with R = 1 is said to have even R-parity, while a particle with R = -1 is said to have odd R-parity. Normal particles, such as fermions, gauge bosons, and Higgs particles, are even, while their supersymmetric partners, which are the sfermions, gauginos, and higgsinos, are odd. Since R-parity is conserved in the MSSM, when you multiply the R-parities of the incoming particles of a Feynman diagram, it must be the same as what you get when you multiply the R-parities of the outgoing particles. Therefore, all interactions involve an even number of supersymmetric particles, or sparticles. In the supersymmetry Feynman diagrams, each trilinear vertex includes either zero or two supersymmetric partners to normal particles, which may be either incoming or outgoing particles. This means that supersymmetric particles are produced in pairs from the decay of normal particles. It also means that when a supersymmetric particle decays into two particles, one of the two is also a supersymmetric particle. Hence, in the MSSM, the lightest supersymmetric particle, or LSP, must be stable. Since LSP's can't decay, they must have survived from shortly after the Big Bang, before supersymmetry was broken. If the LSP was electrically charged or colored, it would bind with other particles to create exotic isotopes. Since no exotic isotopes have been detected, some people conclude that the LSP must be electrically neutral and colorless, although exotic isotopes could still exist if they were very massive. If the LSP is electrically neutral and colorless, it would be detected by the fact it carried away energy-momentum from a reaction, similar to a massive neutrino.
The LSP is an obvious candidate for dark matter. The photino, zino, higgsinos, and the axino, the supersymmetric partner of the axion, are candidates for cold dark matter. The gravitino is a candidate for warm dark matter. It should also be pointed out that conservation of R-parity is part of the MSSM, which was built on the assumption of strict minimality. However, you could come up with a more complicated SUSY model which violated conservation of R-parity, and then the LSP would not be stable after all. Which sparticle is the LSP? Many people take it to be the photino, which would be electrically neutral and colorless, although there is no way to know. It actually may be the result of a quantum mechanical mixture analogous to the KM-matrix or the neutrino mass matrix. The LSP is typically chosen to be a spin-½ particle called a neutralino, which is its own antiparticle, and is a linear combination of the photino, zino, higgsinos, and axino. In much of the parameter space, the neutralino is a bino, a particular linear combination of the photino and zino. All these possible LSP's are weakly interacting massive particles, or WIMP's, and would therefore be cold dark matter.
Supersymmetry allows the following vertices.
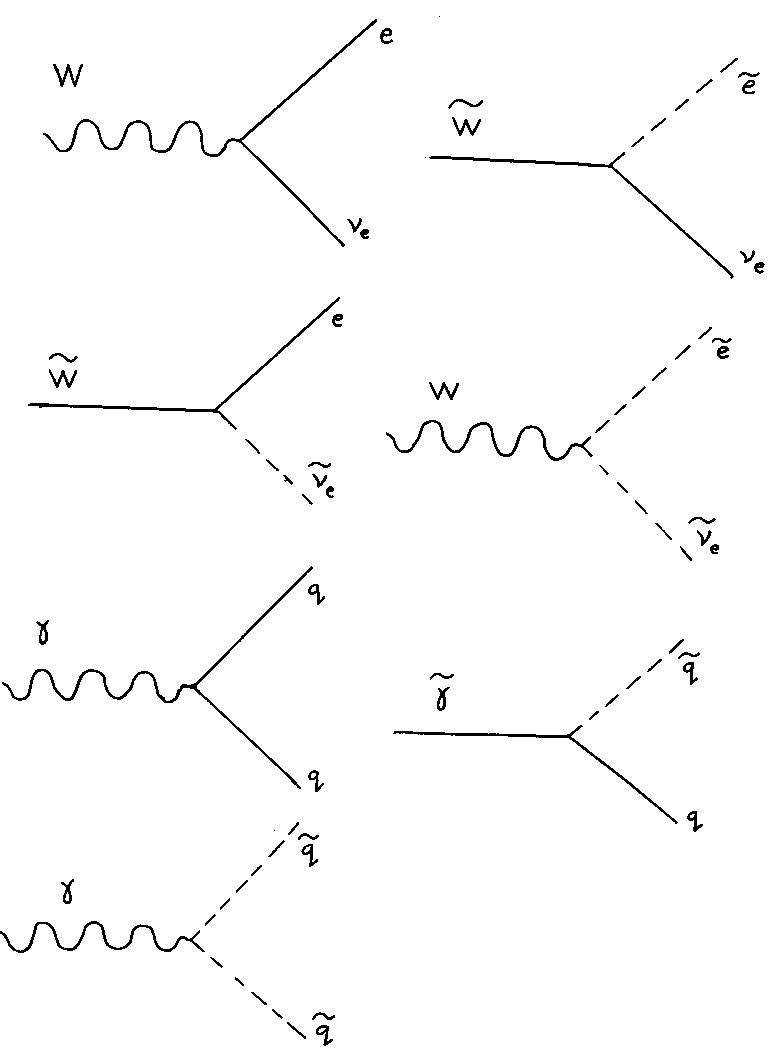
The MSSM Lagrangian, including the soft breaking terms I gave earlier, is as follows.
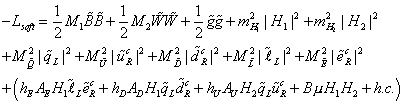
-Lsoft = ½ M1 [B tilda] [B tilda] + ½ M2 [W tilda] [W tilda] + ½ M3 [g tilda] [g tilda] + mH12 | H1 |2 + mH2 | H2 |2 + M[Q tilda]2 | [q tilda]L |2 + M[U tilda]2 | [u tilda]Rc |2 + M[D tilda]2 | [d tilda]Rc |2 M[L tilda]2 | [l tilda]L |2 + M[E tilda]2 | [e tilda]Rc |2 + (hE AE H1 [l tilda]L eRc + hD AD H1 [q tilda]L [d tilda]Rc + hU AU [q tilda] [u tilda]Rc + BuH1 H2 + h. c.
where M1, M2, and M3 are U(1), SU(2), and SU(3) gaugino masses, mH12, mH22, and Bu are mass terms for the Higgs fields. The scalar mass terms M[Q tilda]2, M[U tilda]2, M[D tilda]2, M[L tilda]2 are in general hermitian 3 x 3 matrices. All the parameters are complex, so we end up with 124 free parameters, which are the masses, phases, and mixing angles. Lsoft respects R-parity.
The Higgs potential gets contributions from supersymmetric F-terms, supersymmetric D-terms, and SUSY-breaking terms, which altogether give
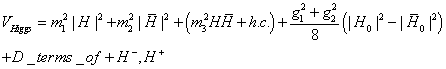
VHiggs = m12 | H |2 + m22 | [H bar] |2 + (m32 H[H bar] + h. c.) + ((g12 + g22)/8) (| H0 | - [H bar]0 |2) + (D-terms of H-, [H bar]+)
where g1 and g2 are the U(1) and SU(2) gauge couplings, and the mass parameters are given by
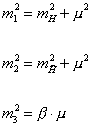
m12 = mH2 + u2
m22 = m[H bar]2 + u2
m32 = B . u
You have
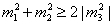
m12 + m22 > 2| m32 |
so m12 and m32 can't both be negative. The origin of the potential is a saddle point. In MSSM, there is a connection between gauge symmetry breaking and SUSY breaking.
You have two complex doublets H and [H bar], so you have eight degrees of freedom. Three become the longitudinal components of the W+, W-, and Z0. That leaves five remaining degrees of freedom. They become a neutral psuedoscalar Higgs boson, two neutral scalar Higgs bosons, a positively charged Higgs boson, and a negatively charged Higgs boson. The physical psuedoscalar Higgs boson is a mixture of the imaginary parts of H0 and [H bar]0 which have the following mass matrix.
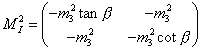
The neutral scalar Higgs bosons are mixtures of the real parts of H0 and [H bar]0 which have the following mass matrix
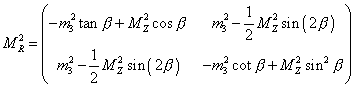
Also, the ratio of the vacuum expectation values of the Higgs fields is given by
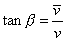
tan[beta] = [v bar]/v
The MSSM allows for gauge coupling unification at MX = 1016 GeV, consistent with grand unified theories. The gauginos are in the same representation of the gauge group. The gaugino masses are also unified at scales Q > MX. The one loop renormalization group equations for the gauge couplings and gaugino masses are
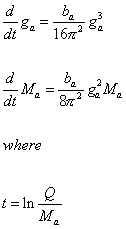
d/dt ga = (ba/16[pi]2) ga3
d/dt Ma = (ba/8[pi]2) ga2 Ma
where
t = ln (Q/Ma)
and the ba coefficients are given by
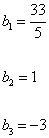
b1 = 33/5
b2 = 1
b3 = -3
For comparison, the ba coefficients for the Standard Model are
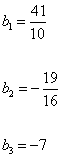
b1 = 41/10
b2 = -19/16
b3 -7
The difference is due to the fact that the MSSM has a richer particle spectrum in the loops. Therefore, for the MSSM, you have
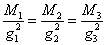
M1/g12 = M2/g22 = M3/g32
at any renormalization group scale up to two loops.
The supersymmetry breaking scale should be around 1 TeV, so supersymmetric particles should be around that mass, in which such case they will be detectable by the Large Hadronic Collider at CERN.
Supersymmetry can also be used as the basis of another mechanism to provide the baryon asymmetry of the Universe, called the Affleck-Dine mechanism. Let’s say you have a colorless electrically neutral combination of quarks and leptons. This object then has a supersymmetric scalar partner, X, that is a combination of squark and slepton fields. In supersymmetric field theories, you have flat directions in field space where the scalar potential vanishes. There are directions in the superpotential along which X is a free massless field. During inflation, the X field is displaced, causing initial conditions for the evolution of the field. There are baryon number violating operators in the potential V(X) which determine the initial phase of the field. You then end up with baryon number violation which could explain the baryon asymmetry of the Universe.
Up to this point, we've only considered the simplest type of supersymmetry, called N = 1 supersymmetry. N measures the number of supersymmetric generators. If you have the supersymmetry generator Q that we've been discussing so far, that's called N = 1 supersymmetry. If you double the number of supersymmetry generators, that's N = 2 supersymmetry. If you double it again, that's N = 4 supersymmetry. If you double it again, that's N = 8 supersymmetry. N = 8 is the highest N considered, since higher N would produce particles with spin more than two, and the graviton, which is spin-2, is considered the highest spin particle in existence. Thus, N can take values of 1, 2, 4, or 8. The number of particles in a supermultiplet is 2N. For N = 1, that gives 21 = 2 particles, one of which is a normal particle, and the other of which is its supersymmetric partner. For N = 2, that gives 22 = 4 particles, one of which is a normal particle, and the other three of which are its supersymmetric partners. In N = 1 supersymmetry, a spin-1 particle has one supersymmetric partner which is spin-½. In N = 2 supersymmetry, a spin-1 particle has three supersymmetric partners, two of which are spin-½, and one of which is spin-0. As you can see, the number of supersymmetric particles rises very rapidly as N increases. However, there are some advantages to considering N > 1. For instance, in N = 4, the beta function is zero.
So far I have discussed grand unified theories and supersymmetry. It's natural to combine these two basic extensions of the Standard Model together. They work better in conjunction than either does alone. There are two basic ways of doing this. One is to take a supersymmetric theory, and embed it within a grand unified theory. The second is to take a grand unified theory, and come up with a supersymmetric version of that. If you supersymmetrize the Standard Model, you get the minimal supersymmetric standard model, or MSSM. If you supersymmetrize SU(5) grand unified theory, you get supersymmetric SU(5). For instance, the X and Y bosons now have supersymmetric partners called xinos and yinos. You have chiral and vector superfields belonging to the [5 bar]-dimensional and 10-dimensional representations. You need the two sets of Higgs superfields belonging to the 5-dimensional and [5 bar]-dimensional representations of SU(5) to generate the fermion masses. You also need the 24-dimensional Higgs field to break the SU(5) group down to SU(3) x SU(2) x U(1). All other fields are supersymmetric generalizations of the fields present in SU(5). The rate of X and Y exchange is determined by their masses, which are determined by the unification scale, which changes when you add supersymmetry, since the renormalization group is different, due to the contributions of both fermions and bosons to the self-energy. Now, in supersymmetry, F-terms can give rise to baryon number violation. Still, the proton lifetime is longer in supersymmetric SU(5) than in normal nonsupersymmetric SU(5). That's an additional advantage of supersymmetry. You can also come up with supersymmetric SO(10). It should be emphasized that both SU(5) and SO(10) suffer from the hierarchy problem, which can only be solved by supersymmetry.
Up until now, we have assumed that supersymmetry was a global symmetry. However, like everything else in physics, it should be a local symmetry. Distant parts of the Universe that aren't casually connected shouldn't be forced to have the same values for various quantities. Remember in my paper on the Standard Model where I talked about making the Lagrangians locally invariant? You have to add extra terms to cancel out the unwanted derivative terms that destroy local invariance, and those added terms can be identified with the gauge bosons. The same thing happens when you try to make supersymmetry locally invariant. If ε is a spinor that generates the SUSY transformations, the gauge invariance will be spoiled by terms involving
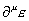
[partial derivative]u [epsilon]
Therefore, you have to add a new gauge field Xu to cancel out the derivative term
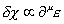
[delta]X is proportional to [partial derivative]u [epsilon]
This gauge boson has a spin of 3/2. You can imagine that this new particle is a supersymmetric partner of another particle with spin-2. You can call this spin-2 particle the graviton, and the spin-3/2 particle, the gravitino. This is an amazing result. Just by making supersymmetry locally invariant, you arrive at a theory that naturally includes gravity. This theory is called supergravity. Supergravity with N > 1 is called extended supergravity. Unfortunately, supergravity is non-renormalizable. All pre-string attempts to quantize gravity are non-renormalizable, and supergravity does nothing to address this problem.
The idea that transformations should be invariant under local coordinate change is of course one of the main principles of general relativity, so in a odd way, you are including an aspect of general relativity in supersymmetry by making it locally invariant, and then as a result, it predicts a spin-2 particle we can identify with the graviton. Unfortunately, any spin-2 point particle gives a non-renormalizable theory, whether it arises naturally, or you put it in by hand. However, there are advantages to supergravity beyond the fact that it predicts the graviton. The difficulties in coming up with spontaneous symmetry breaking for supersymmetry are derived from the fact that supersymmetry is a global symmetry. However, in supergravity, supersymmetry is a local symmetry, so you don't have that problem.