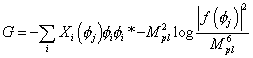
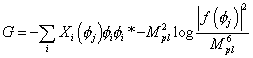
G = -[summation over i] Xi ([phi]j) [phi]i [phi]i* - Mpl2 log (|f([phi]j)|2/Mpl6
where f is the superpotential, and Xi are real functions of the chiral fields φj. Supersymmetry is broken spontaneously if
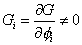
Gi = [partial derivative of G with respect to [phi]i] is not equal to 0.
It is difficult to break supersymmetry using only the fields in the MSSM. Therefore, you introduce a hidden sector which consists of some fields that do not have any gauge or superpotential couplings to the visible sector of the MSSM. The number of free parameters can be greatly reduced by imposing a global U(N) symmetry on the Kahler metric, where N is the number of superfields in the visible sector. Since the MSSM has so many free parameters, this is an additional benefit of supergravity.
Supergravity naturally predicts a spin-2 particle that can be identified with the graviton, but doesn't change the fact that any theory that contains a spin-2 particle is non-renormalizable. In fact, throughout most of the 20th Century, any attempt to quantize gravity was non-renormalizable. This was a problem endemic in all attempts to quantize gravity. Obviously, this problem required a very radical innovative solution. This solution turned out to be string theory. Up until this point, we have assumed that particles were zero-dimensional points. String theory rests instead on the premise that particles are one-dimensional line segments. If the end points of a line segment meet, they can join to form a little loop. Line segments are called open strings, and loops are called closed strings. The way a string oscillates determines what type of particle it appears as. Point particles sweep out world lines, and their Feynman diagrams are networks of lines that meet at vertices. Strings sweep out two-dimensional world sheets or tubes. Their Feynman diagrams are surfaces or tubes that join smoothly without corners.
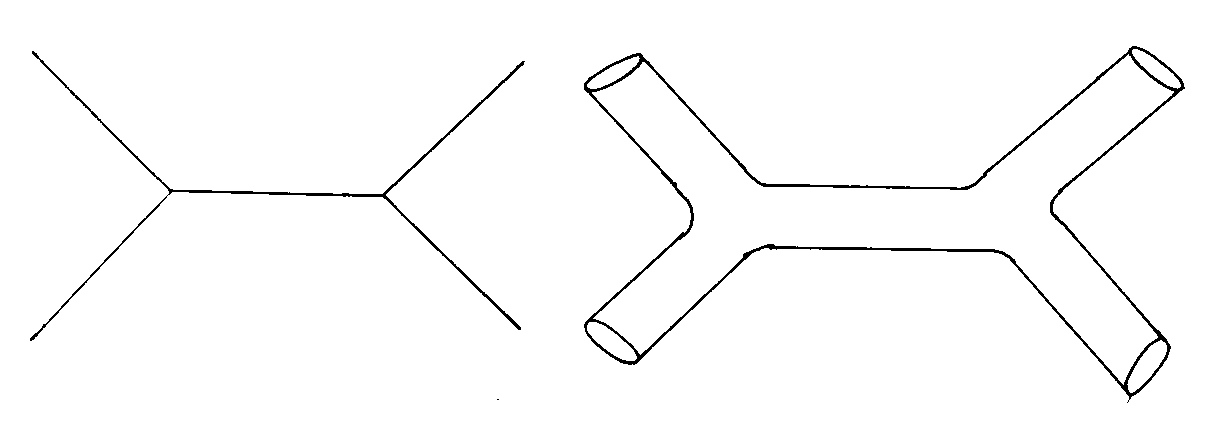
The non-renormalizable infinities originate from trying to describe a spin-2 particle at the vertex of a Feynman diagram. Since there are no vertices in the Feynman diagrams of strings, you don't have that problem. Therefore, you can have a quantum theory of gravity, and successfully unite gravity with the other forces. Not only that, but string theory actually predicts a massless spin-2 particle. String theory plus supersymmetry is called superstring theory. Superstring theory has achieved the ultimate Holy Grail of 20th Century physics, which is one renormalizable quantum theory that accurately describes all four forces of nature, including gravity.
For this reason, superstring theory has been called a "theory of everything". However, some string theorists disagree with that phrase. First of all, it's still a work in progress. We have not yet arrived at a final fully predictive version of superstring theory. Second of all, even when we have a final comprehensive predictive superstring theory, it will not be the final word in physics. It will contain free parameters or so-called fundamental constants that will need further explanation as to why they have the values they do. For instance, what determines which specific manifold the extra dimensions are compactified on? If you look throughout the history of physics, from Ancient Greece to the present day, everyone always assumes that their view of the Universe is close to the truth, and they were close to the final theory of physics. Obviously, that kind of wishful thinking has never been true in the past, it's not true now, and it will never be true in the future. Third of all, superstring theory is useful in many fields of advanced physics, from cosmology to black holes, but no one should expect it to answer every question in every field of physics, and there are some fields, such as chaos theory, that should not benefit from superstring theory at all. Therefore, superstring theory is not a literally a "theory of everything". Having got that disclaimer out of the way, if I may regain the spirit of the previous paragraph, superstring theory ranks among the greatest intellectual achievements of mankind. Nothing should detract from the enormous success that superstring theory has achieved. That success is even more astounding considering the humble origins and history of string theory.
In the 1950's, electromagnetism was very accurately described by QED, but there was no analogous theory for the strong force which acted between the multitude of hadrons, which were at that time considered fundamental. One attempt to describe the strong force was the S-matrix approach, which was originally founded in quantum field theory, but had since evolved into the boot-strap formulation, which was an anti-field theory approach. One strand of S-matrix development was Regge theory, which came to dominate the analysis of the high energy regime. However, then came along the quark model of Murry Gell-Mann and George Zweig, which led to QCD, which was an extremely successful theory of the strong force. Previous alternative theories of the strong force, such as Regge theory, fell by the wayside as defunct historical curiosities.
In 1968, Gabriele Veneziano published a paper on the dual resonance model derived from Regge theory. In the period 1968 - 1973, there were just a few people working on this obscure offshoot of Regge theory. After a couple of years of working on it, it slowly dawned on them that their theory assumed that hadrons were one-dimensional line segments instead of zero-dimensional points, which at the time must have seemed bizarre. In 1970, Yoichiro Nambu, Leonard Susskind, and Holger Nielson determined that this dual resonance model actually requires that particles be thought of as strings. Lenny Susskind claims that for one day, he was the only person in the world who knew it was a theory of strings. At any rate, no one could get the damn thing to work. For one thing, it assumed there were extra spatial dimensions, which they considered obviously impossible. Second of all, the theory was plagued with a massless spin-2 particle, which they considered an aberrant defect, and they couldn't figure out how to get rid of it. Then came along QCD, which was a beautiful successful description of the strong force, so this obscure offshoot of the now defunct Regge theory was dropped by its few adherents.
It was genius of John Schwarz and Joel Scherk of Cal Tech, in 1974, and independently of Tamiaki Yoneya, to recognize the hidden potential of this ugly duckling theory. If this theory naturally has a massless spin-2 particle in its spectrum, which obviously can be identified with the graviton, that raises the hope of possibly being able to unite gravity with the other forces. Instead of hadrons, which were no longer considered fundamental, they imagined that the Standard Model particles were actually strings. If the theory includes gravity, then the string length would be close to the Planck length, which would explain why we detect them as point particles. Also, the extra dimensions would be compactified on the same very small distance scales, which would explain why we don't detect them either. The tension of a string is analogous to the mass of a point particle.
Still, there were serious drawbacks to the first string theory. It only describes bosons, with no fermions at all. It assumed 26 spacetime dimensions. Also, it predicted the existence of a tachyon, assumed to be impossible. However, these problems are solved if you combine string theory with supersymmetry. Supersymmetry would create fermionic partners to the bosons, thus allowing fermions. In superstring theory, there were 10 spacetime dimensions instead of 26. Also, supersymmetry removed the tachyon from the spectrum. Despite this, few people studied superstrings from 1974 - 1984.
During the first superstring revolution, from 1984 - 1985, string theory was transformed from an obscure theory to the forefront of theoretical particle physics. During this time, it was realized that there are actually five different superstring theories, described as follows.
| Type | Open versus Closed | Gauge Group | Parity | Supersymmetry | S dual | T dual |
| Type I | open and closed | SO(32) | violating | one supersymmetry | Heterotic SO(32) | Type IA |
| Type IIA | closed | U(1) | conserving | two supersymmetries | none | Type IIB |
| Type IIB | closed | none | violating | two supersymmetries | Type IIB | Type IIA |
| Heterotic SO(32) | closed | SO(32) | violating | right-movers supersymmetric left-movers not | Type I | Heterotic E8 x E8 |
| Heterotic E8 x E8 | closed | E8 x E8 | violating | right-movers supersymmetric left-movers not | none | Heterotic SO(32) |
Type I strings are open, and the rest are closed. Of course, if the ends of an open string meet, it forms a closed string, so Type I includes both open and closed strings, while the others include only closed strings. For closed strings, the oscillations of the string, which are little waves on the string itself, can move either to the left or to the right. Waves that move counterclockwise around the loop are called left-movers, and waves that move clockwise around the loop are called right-movers. Left-movers and right-movers do not interfere with each other. For Type IIA and Type IIB superstrings, both the left-movers and right-movers are supersymmetric. For the two heterotic superstring theories, the right-movers are supersymmetric, and the left-movers are non-supersymmetric. Type IIA is parity conserving, in contradiction to reality, although later it was figured out how to induce parity violation in the compactification process. The heterotic strings were discovered in 1984 by Gross, Harvey, Martinec, and Rohm.
The second superstring revolution, from 1994 - present, brought non-perturbative string physics within reach. It was realized that the five string theories are related to each other through dualities. If theory A at strong coupling, meaning with a large strength of interaction, is equivalent to theory B at weak coupling, they are S-dual. If theory A compactified on a space of large volume is equivalent to theory B compactified on a space of small volume, they are T-dual. If theory A compactified on a space of large volume is equivalent to theory B at strong coupling, they are U-dual. T-duality, unlike S-duality or U-duality, can be understood perturbatively, and thus was discovered between the two string revolutions. If two theories A and B are S-dual, they are related by
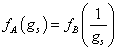
fA (gs) = fB = (1/gs)
where gs is the string coupling constant. Two of the superstring theories, Type I and Heterotic SO(32), are related by S-duality. Type IIB is self-dual under S-duality. Thus, S-duality is a symmetry of Type IIB theory. This symmetry is broken if gs = 1. Because of S-duality, the strong coupling behavior of each of these three theories is determined by a weak coupling analysis. The remaining two theories, Type IIA and Heterotic E8 x E8 behave very differently at strong coupling. They change from 10-dimensional to 11-dimensional.
If two theories are T-dual, they are related by
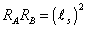
RA RB = (ls)2
where R is the radius of the compactified dimension, and ls is the string length. When one of the circles becomes small, the other becomes large. Type IIA and IIB are T-dual to each other. Heterotic SO(32) and Heterotic E8 x E8 are T-dual to each other. These various dualities led to the conclusion that all five string theories are related to each other, and are in fact, just limiting cases of a single underlying theory, that we now usually call M-theory.
Until 1995, it was only understood how to formulate string theories in terms of perturbation expansions. Perturbation theory is useful in a quantum theory that has a small dimensionless coupling constant, since it allows you to compute physical quantities as power series expansions in the small parameters. For a physical quantity T(α), you compute using Feynman diagrams.
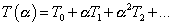
T([alpha]) = T0 + [alpha] T1 + [alpha]2 T2 + …
For QED, the fine structure constant is
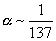
[alpha] ~ 1/137
For QED, this process works because α is so small. Each term is much smaller than the previous term, so you can neglect higher terms. However, more generally, there are various non-perturbative contributions, such as instantons, that have the structure
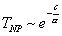
TNP ~ e-(c/[alpha])
where c is a constant. In QCD, at high energy, perturbation theory is useful due to asymptotic freedom. At low energy, it is not, due to confinement, and you have to use other methods, such as lattice QCD.
In string theory, the dimensionless string coupling constant, gs, is determined dynmamically by the vacuum expectation value of a scalar field called the dilaton. Right now, it's essentially a free parameter you can make anything you want, but there is no reason to assume that it is small. Therefore, it's good to be able to study string theory non-perturbatively.
The other major advance of the second superstring revolution was the study of the boundary conditions of open strings. There are 10 dimensions, 9 of space, and one of time. Let's say the end points of an open string can propagate freely through all spatial dimensions. These are called Neumann boundary conditions. However, the endpoints of an open string could also be fixed, and not free to move. This is called Dirichlet boundary conditions. The endpoint of an open string could be fixed in some dimensions and not others. For instance, it could be fixed in seven of the nine spatial dimensions, and free to move in the other two. It would then be free to slide around in a two-dimensional plane. That two-dimensional surface could then be considered a physical object called a Dirichlet membrane, or D-brane. If the endpoints of an open string had p Neumann boundary conditions, it therefore has 9 - p Dirichlet boundary conditions, and ends on a Dp-brane.
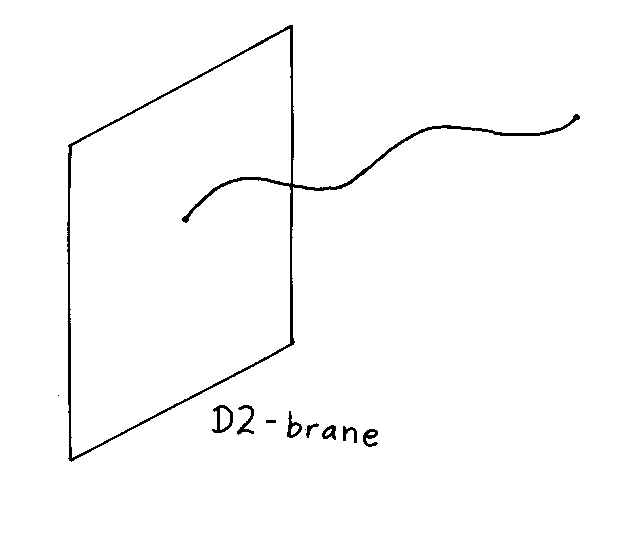
You could think of a string as simply a 1-brane, although remember that branes are defined in terms of strings ending on them, whereas strings are postulated from the beginning. D-branes were discovered/invented by Joseph Polchinski in 1995.
All the string theories have a second rank tensor field called Buv, called the Kalb-Ramond field. A particle, such as an electron, can be charged under the photon field, which is a vector field Au, which then gives the electron stability, due to conservation of charge. In the same way, strings themselves are charged under the second rank tensor field Buv, and this gives strings stability.
Since string theory talks a lot about compactifying spaces, I should discuss some basic topology. I said at the beginning of my paper on the Standard Model, that mathematicians try to go from the specific to the general. In geometry, that takes the form of topology. In traditional geometry, a regular polygon is considered the same shape if you do a translation, rotation, or reflection, but not if you do a deformation, such as changing the angles, the lengths of the sides, the number of sides, or the curvature of the sides, from flat to curved. Topology uses an expanded definition of “same shape”, so it is still considered the same shape under the other manipulations I listed. All regular polygons, irregular polygons, a circle, an ellipse, etc. are all considered the same shape, which for simplicity, is represented by the circle. In other words, they are topologically equivalent.
Special relativity assumes a flat background metric called Minkowski space. General relativity generalizes this by allowing curved space. This potentially curved space is called a manifold. The simplest manifold is flat space. In geometry, this is called Euclidean space, or Rn, the set of n-tuples (x1, x2, …xn) More generally, a manifold is a space that locally looks like Rn. The space may be curved and have a complicated topology, but in local regions, it looks just like Rn. The entire manifold is constructed by smoothly sewing together these local regions. The simplest manifold is, of course, n-dimensional Euclidean space, Rn, since it obviously looks like Rn not just locally but globally. A one-dimensional line is called R1. A two-dimensional plane is R2. Three-dimensional space is R3.
The second simplest manifold is the n-sphere, Sn. This is defined as the locus of all points some fixed distance from a given point in Rn + 1 space. A circle is called S1. A sphere, which topologists call a two-sphere, is S2. A hypersphere, or three-sphere, is S3. Notice n is the dimensionality of the surface, not the entire thing which exists in n + 1 dimensions.
The next simplest manifold is the n-torus, Tn. A torus is a surface of revolution formed by a circle being rotated about a coplanar line outside the circle. You can form a torus from a square or rectangle. Imagine, you have a square, and you roll it up and join two opposite sides, and form a cylinder. Then you bend the cylinder into a circle, and attach the two opposite ends to form a torus. More generally, an n-torus, Tn is formed by taking an n-dimensional cube, and attaching all opposite sides to each other. What we normally think of as a torus is called a two-torus or T2.
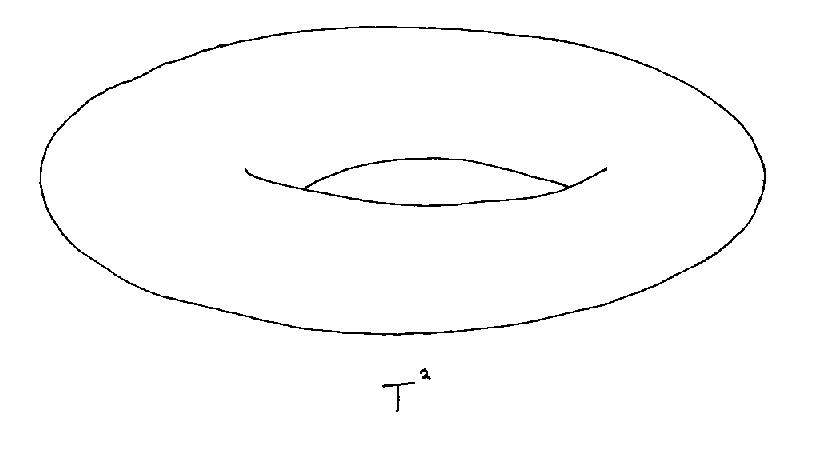
A torus has one hole. However, an acceptable manifold could have any number of holes. You can represent the number of holes in a torus by the genus. A Riemann surface of genus g is a two-torus with g holes instead of one. A sphere, S2, is a Riemann surface of genus zero. A two-torus, T2, is a Riemann surface of genus one. A torus-like shape with two holes is a Riemann surface of genus two. Every compact orientable boundaryless two-dimensional manifold is a Riemann surface of some genus.
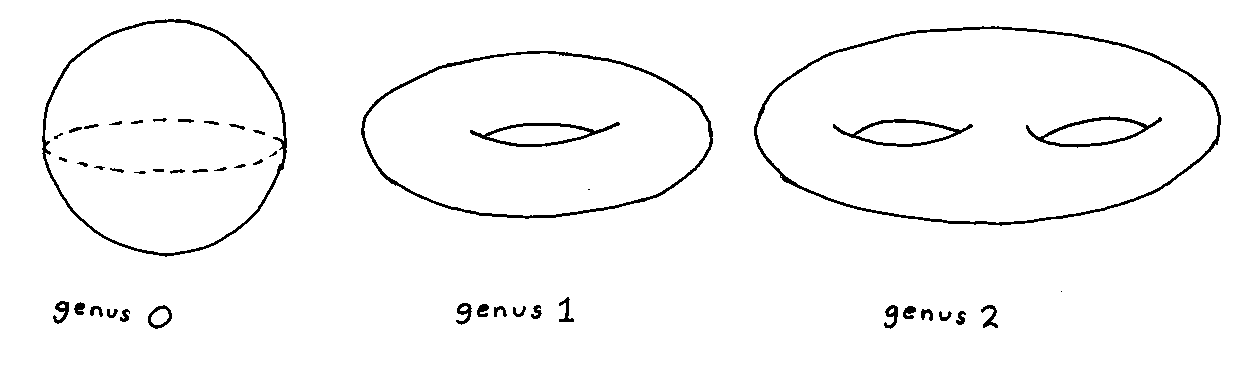
The genus 2 manifold is called a double-torus, or the connected sum of two tori, and is symbolized by T2 # T2. All of the above manifolds are orientable manifolds, which means they have two sides. If you look at a plane, R2, you’re either on one side or the other. If you have a sphere, S2, any point not on the surface is either inside or outside. An example of a non-orientable manifold would be a klein bottle, K2 or KB, which only has one side to it. It was invented by Felix Klein in 1882. Despite what it may look like in the diagram, it does not intersect itself. It uses the fourth spatial dimension to jump over itself.

If a manifold extends infinitely, such as a line or plane, it is called non-compact. If a manifold has a finite area, such as a circle, sphere, or torus, it is called compact. A manifold does not have to be a geometric shape. A set of continuous transformations, such as rotations in Rn, forms a manifold. Lie groups are manifolds with group structure. Also, the direct product of two manifolds is a manifold. If you take two manifolds M and M' of dimensions n and n', you can construct a manifold M x M' of dimension n + n'.
A manifold could have no boundaries, such as a line, circle, plane, sphere, or all the other examples I've listed so far, or it could have boundaries, such as an interval, disk, ball, finite cylinder, Möbius strip, or "pair of pants".
What is not a manifold? A topology is not a manifold if there is somewhere that is does not locally look like Rn. Examples include a one-dimensional line attached to a two-dimensional plane, or two cones attached at the vertices.
Now let's look at an example of a product of two manifolds. Let's say one is a line, R1, and the other is a circle, S1. Since each is one dimensional, their product would be 1 + 1 = 2 dimensional. Their product would be R1 x S1, which is an infinite cylinder. Notice that the cross section along the axis of the cylinder is parallel lines, each of which is R1, and the cross section perpendicular to the axis of the cylinder is a circle, which is S1.
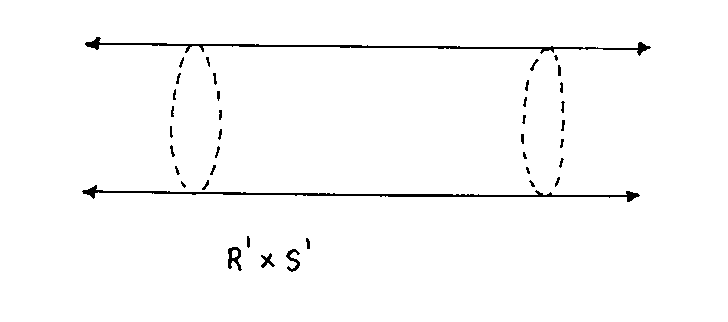
If the radius of the circle was very small, the cylinder would be indistinguishable from a line. Imagine a rubber garden hose. On a scale of tens of meters, it can be treated as a one-dimensional line. On a scale of centimeters, it looks like a two-dimensional surface, although you can still detect the curvature, and it should be treated like a cylinder. On a scale of a millimeter or less, you could treat it like a flat plane. You see how on a scale of tens of meters, it appears one-dimensional when it's really a two-dimensional surface. Thus, if one of the dimensions is compactified on a circle the radius of which is very small compared to the size scale at which you're looking at, it would appear to have one less dimension. R1 x S1 would look like R1 if the radius of S1 was very small. If you were in a R3 x S1 manifold, which is four-dimensional, and the radius of S1 was the Planck length, you would think you were in a R3 manifold, which is three-dimensional. In this way, the 10-dimensional spacetime assumed in string theory appears to us as 4-dimensional spacetime. The other six dimensions are compactified on a scale of the Planck length,10-35 meters, so obviously we can't detect them.
Since the equations must be satisfied, the geometry of the six-dimensional space is not arbitrary. What works best is a type of manifold called a Calabi-Yau manifold, which is a Kahler manifold with vanishing first Chern class. In 1954, Eugenio Calabi first theorized the possibility of such a thing. In 1976, Shing-Tung Yau proved the Calabi conjecture, and discovered Calabi-Yau space. In 1985, Candelas, Strominger, Horowitz, and Witten proposed that the extra dimensions required by string theory could be compactified on a Calabi-Yau manifold. You can't draw a picture of it since it's six-dimensional, and has no analog is three dimensions. Calabi-Yau compactification, in the context of E8 x E8 heterotic superstring theory, can give a low energy effective theory that closely resembles a supersymmetric extension of the Standard Model. Superstring theory, therefore usually assumes that our Universe corresponds to a M x CY manifold, where M is Minkowski space, and CY is a Calabi-Yau manifold. There are several Calabi-Yau spaces, and if you choose the one with the correct topology, the resulting theory predicts that you should have three generations of quarks and leptons. It is very encouraging that you can get the right results by choosing the correct topology, although you would prefer to have a deeper motivation for why you choose that topology. In other words, you can choose the values of free parameters to fit what you observe, although the question remains as to why they have those values.
A Joyce manifold, or Riemannian manifold with G2 holonomy, is a 7-dimensional manifold for which each tangent space is equipped with all the structure of the imaginary octonions. M-theory is an 11-dimensional theory, and you can compactify seven of the dimensions on a Joyce manifold in order to leave the four spacetime dimensions we're familiar with.
It is worthy of mention that the idea of uniting gravity with the other forces by assuming extra compactified dimensions goes back to the work of Theodore Kaluza in 1919, and later expanded by Oskar Klein in 1926. At that time, the only other force known was electromagnetism. In Kaluza-Klein theory, the extra dimension in a five-dimensional version of general relativity is compactified on a circle, giving rise to a new local U(1) symmetry which can be identified with electromagnetism. Of course, it was actually easier to unite gravity and electromagnetism at that time, since they didn't have to develop a quantum theory of gravity, since quantum theory itself had not yet been invented. Indeed, it was the invention of quantum mechanics, and the inability to quantize gravity, which was why Kaluza-Klein theory didn't really go anywhere, although the view of modern physics has some similarities to some aspects of it.
Any theory that unites gravity with quantum field theory must involve the three fundamental constants, the universal gravitational constant, G = 6.674215 x 10-11 Nm2/kg2 or m3/kgs2, Planck's constant, h = 6.626176 x 10-34 Js, or [h bar] = h/2π = 1.05 x 10-34 Js, and the speed of light, c = 2.99792458 x 108 m/s. These three fundamental constants can be combined to create quantities with the units of mass, length, and time. They are called the planck mass, planck length, and planck time.
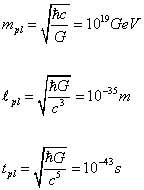
mpl = [square root of ([h bar]c/G)] = 1019 GeV
lpl = [square root of ([h bar]G/c3)] = 10-35 m
tpl = [square root of ([h bar]G/c5)] = 10-43 s
Max Planck first listed his set of units in May 1899 in a paper presented to the Prussian Academy of Sciences. The planck time is the smallest unit of time it's possible to talk about. The planck length is the smallest unit of length it's possible to talk about. The planck mass is the highest energy scale it's possible to talk about. The planck time after the Big Bang, the Universe had a energy of the planck mass, and at that energy, gravity had the same strength as the other forces, which is the same as the situation today at distances as short as the planck length. The extra dimensions would be compactified on the scale of the planck length. The string length might also be at that scale, or might be two orders of magnitude larger, which is still so small that they would appear as point particles to us.
Remember that E = mc2 so in naturalized units where c = 1, E = m, which is why we can measure mass in units of energy, such as electron volts. In this context, the planck mass, 1019 GeV, is of fundamental significance as the highest possible energy scale, and the scale at which gravity is as strong as the other forces. If instead, you measure the planck mass in units of mass, you get 10-8 kilograms, which is about the mass of biological cell, and has no cosmological significance. People have also come up with various derived planck units. The planck temperature Tpl = (c5[h bar]/G)1/2/k = 1032 Kelvin, is the temperature of the Universe a planck time after the Big Bang, where k is Boltzmann’s constant. The planck density is ρpl = mpl/(lpl)3 = 1096 kg/m3 is the density of the Universe a planck time after the Big Bang. The planck force is Fpl = c4/G = 1043 newtons, and some have suggested that this could be the tension of a string. The planck area is the square of the planck length, and the planck volume is the cube of the planck length.
Before we look at strings in more detail, let's review the familiar case of a traditional point particle. In what follows, we'll use the variable
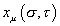
xu ([sigma], [tau])
where σ parametrizes the position of a point on a string, and τ gives the time evolution. Since a point particle doesn't have a position on a string, you just have
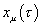
xu ([tau])
that describes how the world line, parametrized by τ, is embedded in the spacetime, whose coordinates are given by xu. For simplicity, let's assume that spacetime is flat Minkowski space with a Lorentz metric.
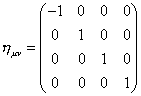
nuv = Diag [-1, 1, 1, 1]
You could, of course, assume a curved spacetime by replacing nuv by a metric guv (x). Assuming Minkowski space, the Lorentz invariant world line element in given by
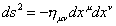
ds2 = -nuv dxu dxv
Assuming [h bar] = c = 1, the action for a particle of mass m is given by
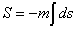
S = -m [integral] ds
In terms of the embedding functions xu (t), the action can be rewritten in the form
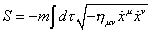
S = -m [integral] d[tau] [square root of (-nuv [x dot]u [x dot]v)]
where dots represent τ derivatives. This action is invariant under local reparametrizations. This is a kind of gauge invariance, where the form of S is unchanged by an arbitrary reparametrization of the world line.
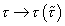
[tau] -> [tau] ([tau tilda])
We require that the function τ ([τ tilda]) is smooth and monotonic.

[derivative of [tau] with respect to [tau tilda]] > 0
The reparametrization invariance is a one-dimensional analog of the four-dimensional general coordinate invariance of general relativity. This kind of symmetry is called diffeomorphism invariance.
The reparametrization invariance of S allows you to choose a gauge. Let's choose the static gauge.
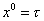
x0 = [tau]
In this gauge, renaming the parameter t, the action becomes
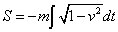
S = -m [integral] [square root of (1 - v2)] dt
where
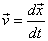
v = [derivative of x with respect to t]
Requiring this action to be stationary under an arbitrary variation of x (t) gives the Euler-Lagrange equations.
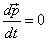
[derivative of p with respect to t] = 0
where
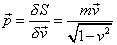
p = [delta]S/[delta]v = (mv)/([square root of (1 - v2)]
The usual relativistic kinematics follows from the action
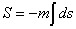
S = -m [integral] ds
Now, let's take what we just did for a point particle, and do the same thing for a p-brane of tension Tp. For p = 0, you have a 0-brane, which is a point particle. For p = 1, you have a 1-brane, which is a string. You could think of it as a generalization of what we just did, except we are no longer assuming p = 0. For p = 0, the tension Tp is what we call the mass. Just as a point particle sweeps out a world line, a p-brane sweeps out a world-volume with p + 1 dimensions. The action in this case involves the invariant (p + 1)-dimensional volume, and is given by
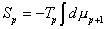
Sp = -Tp [integral] dup + 1
where the invariant volume element is
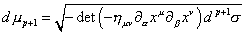
dup + 1 = [square root of (- det (-nuv [partial derivative][alpha] xu [partial derivative][beta] xv) dp + 1 [sigma])]
Here the embedding of the p-brane into d-dimensional spacetime is given by the functions xu (σα). The index α = 0, 1, …p labels the p + 1 coordinates σα of the p-brane world volume, and the index u = 0, 1, …d - 1 labels the d coordinates xu of the d-dimensional spacetime. You have
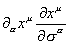
[partial derivative][alpha] [partial derivative of xu with respect to [sigma][alpha]]
The determinant acts on the (p + 1) x (p + 1) matrix whose rows and columns are labeled α and β. The tension Tp is the mass per unit volume of the p-brane. For a 0-brane, meaning a point particle, it's just the mass.
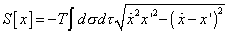
S[x] = -T [integral] d[sigma] d[tau] [square root of ([x dot]2 x'2 - ([x dot] . x')2]
where
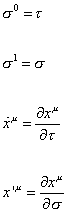
[sigma]0 = [tau]
[sigma]1 = [sigma]
[x dot]u = [partial derivative of xu with respect to [tau]]
x'u = [partial derivative of xu with respect to [sigma]]
This action is called the Nambu-Goto action, and was first proposed by Yoichiro Nambu and Goto in 1970.