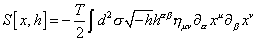
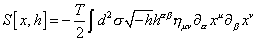
S[x, h] = -(T/2) [integral] d2 [sigma] [square root of -h] h[alpha][beta] nuv [partial derivative][alpha] xu [partial derivative][beta] xv
where
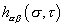
h[alpha] [beta] ([sigma], [tau])
is the world-sheet metric, and h = det hα β. The Euler-Lagrange equation obtained by varying hα β is
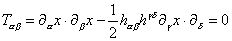
T[alpha] [beta] = [partial derivative][alpha] x . [partial derivative][beta] - (1/2) h[alpha] [beta] h[gamma] [delta] [partial derivative][gamma] x . [partial derivative][delta] x = 0
In addition to reparametrization invariance, the action S[x, h] has another local symmetry called conformal invariance or Weyl invariance. It is invariant under the following transformation
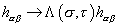
h[alpha] [beta] -> [capital lambda] ([sigma], [tau]) h[alpha] [beta]
This local symmetry is unique to strings, meaning the p = 1 case. These two reparametrization invariance symmetries of S[x, h] allow you to choose a gauge in which the three functions hα β, which is a symmetric 2 x 2 matrix, are expressed in terms of just one function. You can write the conformally flat gauge
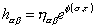
h[alpha][beta] = n[alpha][beta] e[phi]([sigma], [tau])
where ηα β is the two-dimensional Minkowski metric on a flat world sheet. However, because of the factor eφ, hα β is only conformally flat. Using this gauge choice for S[x, h] leaves the gauge-fixed action
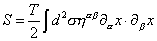
S = (T/2) [integral] d2 [sigma] n[alpha] [beta] [partial][alpha] x . [partial derivative][beta] x
However, this does not take into account quantum mechanics. You should perform a Feynman path integral. When you do this, you find that φ does not decouple from the answer. It only works when d = 26. Otherwise, there are correction terms that can be traced to a conformal anomaly, meaning a quantum mechanical breakdown of the conformal invariance.
The gauge-fixed equation is quadratic in the x's. It is the same as a theory of d free scalar fields in two dimensions. The equations of motion obtained by varying xu are simply free two-dimensional wave equations.
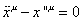
[x double dot]u - x''u = 0
You also have to take into account the constraints, Tα β = 0, which are
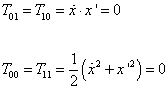
T01 = T10 = [x dot] . x' = 0
T00 = T11 = ½ ([x dot]2 + x'2) = 0
which gives you
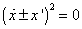
([x dot] ± x')2 = 0
We saw that d = 26, meaning the bosonic string theory has 26 dimensions. Let's show in more detail why this is. If α0 is the vacuum energy, you evaluate it using the following regularization.
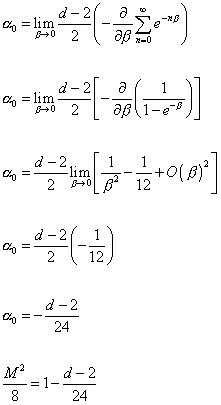
[alpha]0 = lim [beta] -> 0 ((d-2)/2) (-[derivative with respect to [beta]] [summation over n to infinity] e-n[beta])
[alpha]0 = lim [beta] -> 0 ((d-2)/2) (-[derivative with respect to [beta]] (1/(1 - e-[beta])))
[alpha]0 = ((d - 2)/2) lim [beta] -> 0 [(1/[beta]2) - (1/12) + O([beta])2]
[alpha]0 = ((d - 2)/2) (-1/12)
[alpha]0 = -(d - 2)/24
M2/8 = 1 - (d - 2)/24
The only way this level is compatible with Lorentz invariance is if this level is massless. In the above equation M = 0 only if d = 26. Therefore, the bosonic string requires 26 spacetime dimensions.
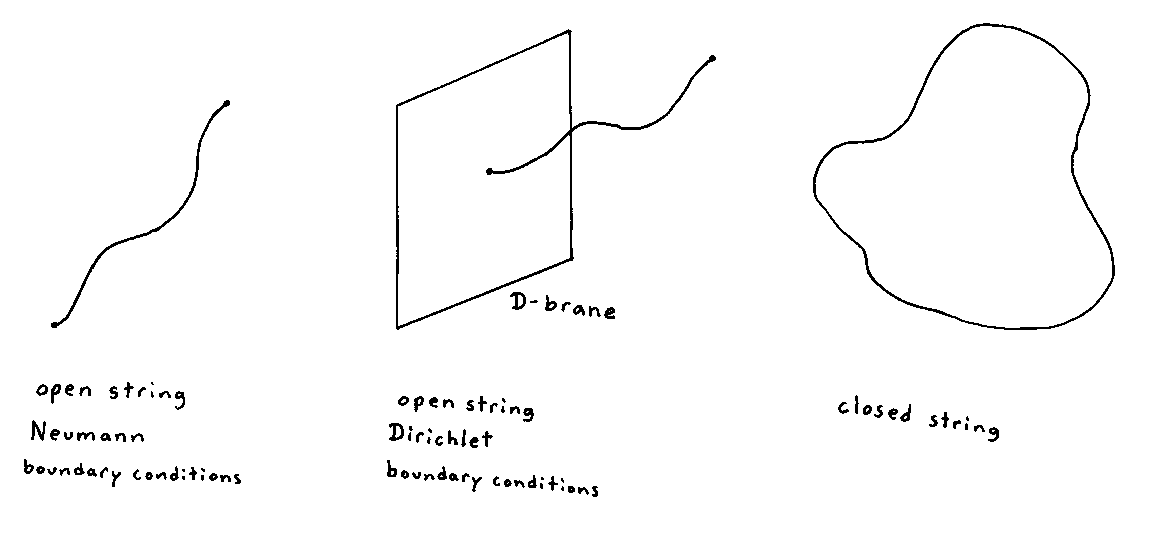
Next, we will discuss the boundary conditions. A string can be open or closed. If it's open, it could have either Neumann or Dirichlet boundary conditions.
For a closed string, by convention, the spatial coordinate changes by π as you go around the string once. Therefore, you have
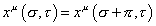
xu ([sigma], [tau]) = xu ([sigma] + [pi], [tau])
For an open string, which has two ends, each end is required to satisfy either Neumann or Dirchlet boundary conditions, for each value of u.
Neumann boundary conditions
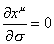
[partial derivative of xu with respect to [sigma]] = 0
for each end, meaning for when σ = 0 or π
Dirichlet boundary conditions
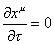
[partial derivative of xu with respect to [tau]] = 0
for each end, meaning for when σ = 0 or π
The Dirichlet condition can be integrated, and then it specifies a spacetime location on which a string ends. Today, most people think of open strings as always ending on D-branes, so for Neumann boundary conditions, people imagine the string ending on a D-brane that fills all of space, so the string end can be located anywhere.
For a closed string, the general solution of the two-dimensional wave equation is given by a sum of the right-movers and left-movers. If waves on a closed string are propagating clockwise, that's called a right-mover, and is represented by
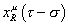
xRu ([tau] - [sigma])
If waves on a closed string propagate counterclockwise, that's called a left-mover, and is represented by
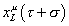
xLu ([tau] + [sigma])
The general solution is the sum of them, which is
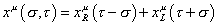
xu ([sigma], [tau]) = xRu ([tau] - [sigma]) + xLu ([tau] + [sigma])
These are subject to the following additional constraints.
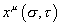
xu ([sigma], [tau])
is real
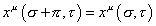
xu ([sigma] + [pi], [tau]) = xu ([sigma], [tau])
and
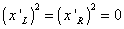
(x'L)2 = (x'R)2 = 0
These are called the Tα β = 0 constraints. The first two of the three conditions can be solved using a Fourier series.
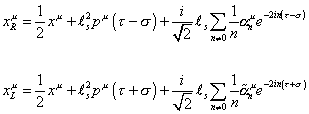
xRu = (1/2) xu + ls2 pu ([tau] - [sigma]) + (i/[squarerooot of 2]) ls [summation over n which is not 0] (1/n) [alpha]nu e-2in([tau] - [sigma])
xLu = (1/2) xu + ls2 pu ([tau] + [sigma]) + (i/[squarerooot of 2]) ls [summation over n which is not 0] (1/n) [alpha tilda]nu e-2in([tau] + [sigma])
where the expansion parameters satisfy
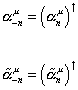
[alpha]-nu = ([alpha]nu)†
[alpha tilda]-nu = ([alpha tilda]nu)†
The center of mass coordinate xu, and the momentum pu are real. The fundamental string length scale ls is related to the tension T by
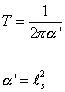
T = (1/2[pi] [alpha]')
[alpha]' =ls2
The parameter α' is called the universal Regge slope. This harkens back to the old Regge theory. The string modes lie on linear parallel Regge trajectories with this slope.
Next we set up the commutation relations to quantize the string. It's the same for closed string left-mover modes, closed string right-mover modes, and open string modes, so we'll just look at the closed string right-movers. Using the gauge-fixing action, the canonical momentum of the string is
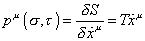
pu ([sigma], [tau]) = [partial derivative of S with respect to [x dot]] = T [x dot]u
Canonical quantization, which is just the tree level 2D field theory for scalar fields, gives
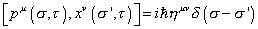
[pu ([sigma], [tau]), xv ([sigma]', [tau])] = i[h bar] nuv [delta] ([sigma] - [sigma]')
In order to quantize the string, it must obey the following commutation relations. Using Fourier modes
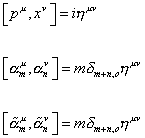
[pu, xv] = inuv
[[alpha]mu, [alpha]nv] = m[delta]m + n, o nuv
[[alpha tilda]mu, [alpha tilda]nv] = m[delta]m + n, o nuv
and all other commutators vanish. Note that α-mu are like creation and annihilation operators. When you consider operators, you should write them in normal ordered form, where the creation operators are on the left, and annihilation operators are on the right. A quantum mechanic harmonic oscillator can be described in terms of raising and lowering operators, called a† and a, which satisfy
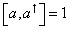
[a, a†] = 1
You can see that aside from a normalization factor, the expansion coefficients α-mu and αmu are raising and lowering operators. You might have noticed that because
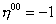
n00 = -1
the time components are proportional to oscillators with the wrong sign. This could lead to negative probabilities. However, the Tα β = 0 constraints eliminate the negative norm states from the physical spectrum.
Now, a closed string is like a circle, so let's take the group of diffeomorphisms of the unit circle, and take it's Lie algebra. That Lie algebra is called the Virasoro algebra. In string theory, you commonly use the Virasoro algebra which is defined as
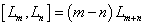
[Lm, Ln] = (m - n) Lm + n
It becomes anomalous once quantum corrections are included, leading to the Virasoro algebra with central charges
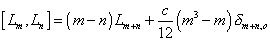
[Lm, Ln] = (m - n) Lm + n + (c/12) (m3 - m) [delta]m + n, o
The second term is called the conformal anomaly term, and the constant c is called the central charge. The generators Ln of the coordinate transformations are related to moments of the two-dimensional energy-momentum tensor T00 - T11 and T01, which vanish due to the gauge-fixing equation.
Another thing you can do is take the group of maps from the unit circle to an arbitrary Lie group. That is called a loop group. Then take the Lie algebra of the loop group, and you get a Lie algebra called the Kac-Moody algebra, which is also used in string theory.
The following defines the Virasoro operators.
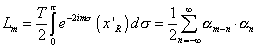
Lm = (T/2) [integral from 0 to [pi]] e-2im[sigma] (x'R) d[sigma] = (1/2) [summation over n from -infinity to infinity] [alpha]m - n . [alpha]n
Since αmu does commute with α-mu, you have to define L0
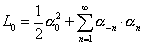
L0 = (1/2) [alpha]02 + [summation over n] [alpha]-n . [alpha]n
where
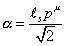
[alpha] = (ls pu)/[square root of 2]
and pu is the momentum.
The following complex vector space is an inner product space
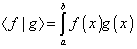
< f | g > = [integral from a to b] f(x) g(x)
This inner product gives us a positive definite norm for each vector
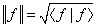
|| f || = [square root of < f | f >]
A Hilbert space is an inner product space which, as a metric, is complete. The Hilbert space of a harmonic oscillator is spanned by states | n >, n = 0, 1, 2, …where the ground state | 0 > is annihilated by the operator
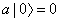
a | 0 > = 0
and
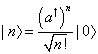
| n > = ((a†)n/[square root of n!]) | 0 >
Then for a normalized ground state
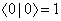
< 0 | 0 > =1
You can use [a†, a] = 1 repeatedly to prove that
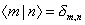
< m | n > = [delta]m, n
and
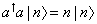
a† a | n > = n | n >
The string spectrum of right-movers is given by the product of an infinite number of harmonic oscillator Fock spaces, one for each αnu, subject to the Virasoro constraints
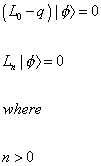
(L0 - q) | [phi] > = 0
Ln | [phi] > = 0, n > 0
where | φ > is the physical state, and q is a constant. It accounts for the arbitrariness in the normal ordering prescription used to define L0. The L0 equation is a generalization of the Klein-Gordon equation. It contains
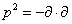
p2 = -[partial derivative] . [partial derivative]
and oscillator terms whose eigenvalue will determine the mass of the state. You have to set the parameter q = 1 so that the mass shell condition becomes
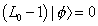
(L0 - 1) | [phi] > = 0
The mathematics of the open string spectrum is the same as the closed string right-movers, so let's use the equations we just obtained to look at the open string spectrum. Here we are assuming all boundary conditions are Neumann, in other words, the D-branes they are attached to fill all of space. The mass shell condition is
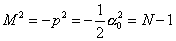
M2 = -p2 = -½ [alpha]02 = N - 1
where p is the momentum, and
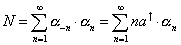
N = [summation over n from 1 to infinity] [alpha]-n . [alpha]n = [summation from n from 1 to infinity] na† . an
where the a†'s and a's are properly normalized creation and annihilation operators. Since a† a has eigenvalues 0, 1, 2, …, the possible values of N are also 0, 1, 2, … You have N = 0 if all the oscillators are in the ground state. Now look at the following equation.
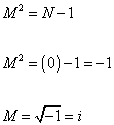
M2 = N - 1
M2 = (0) - 1 = -1
M = [square root of -1] = i
The first particle will then have imaginary mass, which we assume is impossible. In fact, this is another manifestation of the vacuum energy or zero point energy. Remember in my paper on the Standard Model in the section on electromagnetism, and more recently in this paper, in the section on supersymmetry, I gave the following relation for the energy of a particle system.
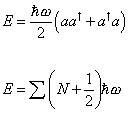
E = ([h bar]w/2) (aa† + a† a)
E = [summation] (N + ½) [h bar]w
When N = 0, the energy is more than zero, meaning the vacuum has energy. Here we are seeing a similar thing again. In this case, it predicts a particle with imaginary mass. What do you call a particle with imaginary mass? It's called a tachyon, which was first theorized by Gerald Feinberg in 1967. If you look at the equation for the Lorentz factor γ, where γ = 1/[squareroot of (1 – (v/c)2)], you will see that if v > c, then γ is imaginary. From that you get imaginary mass. The tachyon has become immensely popular with science-fiction writers because it's supposed to be a particle that travels faster than light. In a certain sense, that's true, but it does not violate special relativity because it would not be possible to use a tachyon to send a message faster than light. Either localized disturbances in the wave equations do not propagate faster than light, or if the waves do seem to move faster than light, the waves are never localized in the first place. Therefore, even if tachyons were to exist, they could not be used to send a message faster than light, so they would not violate special relativity.
It's reminiscent of the so-called EPR paradox in quantum mechanics, where if experiments violate the Bell Inequality, and in a certain sense, a particle could be said to instantly effect a distant particle, it would still not be possible for a person to use this to send a message to another person faster than light. Therefore, it does not violate special relativity.
However, despite its consistency with special relativity, the tachyon is still considered impossible. If they accelerate, they lose energy. A zero-energy tachyon would be infinitely fast. Since a tachyon moves faster than the speed of light in vacuum, it would produce Cerenkov radiation just be traveling though vacuum. Converting part of their radiation to energy, would lower their energy, causing them to accelerate more. Accelerating more would cause them to produce even more energy. You would have a run away reaction, where a tachyon ended up producing an infinite amount of energy, in the form of Cerenkov radiation, out of nothing. If tachyons existed, the vacuum would have to produce tachyon-antitachyon pairs all the time, each of which would undergo this run away effect. Throughout all of space, there would be an infinite number of tachyons, each of which would create an infinite amount of energy out of nothing. The Universe would exist at some sort of infinite energy scale, whereas the Planck scale is considered the highest energy scale possible in the real Universe. Obviously, this is not the Universe we live in. Any theory that predicts a tachyon is a flawed theory. Thus, the string theory we've been discussing so far, the bosonic string, is a flawed theory. However, like I said earlier, supersymmetry can cause the bosonic and fermionic contributions to the vacuum energy to cancel each other out, and leave no vacuum energy. I said that the problem of the tachyon is related to the problem of the vacuum energy, so supersymmetry solves the problem. Therefore, in superstring theory, there is no tachyon.
The ground state of the open string spectrum is
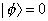
| [phi] > = 0
This gives N = 0, and M2 = 1, or M = i, which is the tachyon, proving that the bosonic string is not a realistic theory. The first excited state in the open string spectrum is
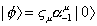
| [phi] > = [zeta]u [alpha]-1u | 0 >
where ζu is the polarization vector of a massless spin-1 particle. This gives N = 1, and M2 = 0, or M = 0. The Virosoro constraint
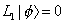
L1 | [phi] > = 0
implies ζu must satisfy
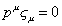
pu [zeta]u = 0
In four spacetime dimensions, a massless particle has two transverse polarization states. More generally, in d dimensions, a massless particle has d - 2 transverse polarization states. One of the dimensions is time. Another one of the dimensions is the longitudinal direction. The rest are transverse polarization states.
The second excited state in the open string spectrum is
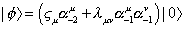
| [phi] > = ([zeta]u [alpha]-2u + [lambda]uv [alpha]-1u [alpha]-1v) | 0 >
This corresponds to N = 2, and M2 = 1, or M = 1. The Virasoro constraint
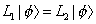
L1 | [phi] > = L2 | [phi] >
restricts ζu and λuv. When d = 26, this state becomes zero norm, and decouples from the theory. This leaves a massive spin-2 particle. There's no such particle in real life. The only spin-2 particle is the graviton, which is massless. However, the fact it predicts a spin-2 particle of any type is a sign we're on the right track.
Next, we'll look at the closed string spectrum. You have both left-movers and right-movers, each of which are the same as the open string states. Therefore, a closed string state is described by a tensor product of a left-moving state and a right-moving state, subject to the condition that the N value of the left-moving state and the right-moving state are the same. The reason for this level matching condition is that we have
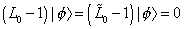
(L0 - 1) | [phi] > = ([L tilda]0 - 1) | [phi] > = 0
The left-movers and right-movers are distinguished by showing a tilda over the right-movers, probably because in heterotic string theories, the right-movers are supersymmetric, although in this case, neither is supersymmetric. The sum
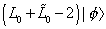
(L0 + [L tilda]0 - 2) | [phi] >
is interpreted as the mass shell condition, while the difference
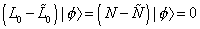
(L0 - [L tilda]0) | [phi] > = (N - [N tilda]) | [phi] > = 0
is the level matching condition. The closed string states are the tensor product of the left-movers and right-movers. Therefore, the closed string ground state is
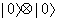
| 0 > x | 0 >
which is a spin-0 tachyon with M2 = -2. Again, this means you have an unstable vacuum. The first excited state is
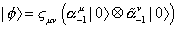
| [phi] > = [zeta]uv ([alpha]-1u | 0> x [alpha]-1v | 0 >)
which has M2 = 0. The Virasoro constraints
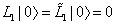
L1 | [phi] > = [L tilda]1 | [phi] > = 0
imply that
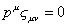
pu [zeta]uv = 0
This polarization tensor encodes three distinct spin states, each of which has a fundamental role in string theory. The symmetric part of ζuv encodes a spacetime metric field guv, corresponding to a massless spin-2 particle, and a scalar field φ, corresponding to a massless spin-0 particle. The spin-2 particle is the graviton. The spin-0 particle is the dilaton. The guv field means that the theory contains general relativity to a good approximation for
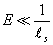
E << 1/ls
where ls is the string length. It's vacuum value determines the spacetime geometry. The value of the dilaton field φ determines the string coupling constant.
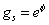
gs = e[phi]
ζuv also has an antisymmetric part, which corresponds to a massless antisymmetric tensor gauge field, called the Kalb-Ramond field. Buv = -Buv It can be viewed as analogous to an electromagnetic field. In electromagnetism, you have the gauge transformation rule for the electromagnetic field.
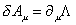
[delta]Au = [partial derivative]u [capital lambda]
You have the gauge-invariant field strength.
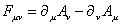
Fuv = [partial derivative]u Av - [partial derivative]v Au
A charged particle is a source of a vector potential Au. The coupling of a charged particle to an electric field is
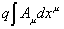
q [integral] Au dxu
and this means that the lightest charged particle, the electron, is stable. Similarly, the Buv field has a gauge transformation of the form
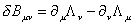
[delta]Buv = [partial derivative]u [capital lambda]v - [partial derivative]v [capital lambda]u
The gauge invariant field strength is
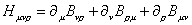
Huvp = [partial derivative]u Bvp + [partial derivative]v Bpu + [partial derivative]p Buv
The fundamental string is a source for the Buv field. This is expressed by the coupling.
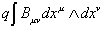
q [integral] Buv dxu [wedge product]dxv
and this means that strings, which are charged under this field, are stable.
The number of physical states is given by
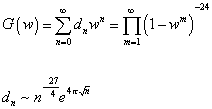
G(w) = [summation over n] dn wn = [product series over m] (1 - wm)-24
dn ~ n(-27/4) e(4[pi] [square root of n])
where G(w) is the generating function, and dn is the number of states, and the exponent 24 reflects the fact that in 26 dimensions, there are 24 polarized states.
Perturbation theory calculations are done by computing Feynman diagrams. In ordinary particle physics, the Feynman diagrams are networks of world lines. In string theory, they are two-dimensional surfaces, which are the world sheets of strings. We assume the world sheet metric hα β is positive definite so the geometry is Euclidean. The diagrams are classified by their topology. With point particles, successively higher terms in the perturbative expansion correspond to an increasing number of internal loops in the Feynman diagrams. With string world sheets or tubes, these correspond to handles. Therefore, the higher the number of terms included in the perturbative expansion, the higher the genus of the manifold that is the world sheet that comprises the Feynman diagram. The Euler characteristic of a manifold is given by
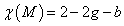
X(M) = 2 - 2g - b
or
X(M) = 2 - 2h - b
where g or h is the genus or number of handles, and b is the number of boundaries. A sphere has no handles and no boundaries, so g = b = 0, and χ = 2 - 2(0) - (0) = 2. A torus has one handle and no boundaries, so g = 1, b = 0, and χ = 2 - 2(1) - (0) = 0. A finite cylinder has two boundaries and no handles, so g = 0, b = 2, and χ = 2 - 2(0) - (2) = 0. A Klein bottle also has a Euler characteristic of 0. Surfaces with χ = 0 admit a flat metric. The order of the expansion, meaning the power of the string coupling constant, is determined by the Euler number of the world sheet.
Leonard Euler (1707 - 1783) came up with many equations or formulas now named after him, and one them stated that if you take any polyhedron, the number of vertices minus the number of edges plus the number of faces is always two. Here are versions of Euler’s formula in 1 – 4 dimensions.
1D → V = 2
2D → V - E = 0
3D → V - E + F = 2
4D → V - E + F - C = 0
where V is vertices, E is edges, F is faces, and C is cells, which are the 3D "faces" of 4D polytopes. So there is a pattern, where with each additional dimension, you add an additional term to Euler's formula, and the sign of the additional terms alternates minus, plus, minus, etc., and the "answer" of the formula alternates 2, 0, 2, 0, etc. This pattern continues for higher dimensions. The reason for the number two is because polygons, polyhedra, and polytopes are circumscribed within the manifold Sn which has an Euler characteristic of two.
In algebraic topology, the Euler characteristic of a space is the alternating sum of the "ranks of the its rational homology groups", and you can compute these using any way of chopping up the space into convex polytopes. Some spaces have an ill-defined Euler characteristic because they either have infinitely many nonzero rational homology groups, typical of infinite-dimensional spaces, or rational homology groups of infinite rank, such as an infinite genus torus. Compact manifolds don’t have these problems. Of course, the Euler characteristic is defined for many spaces other than compact manifolds.
A scattering amplitude is given by the path integral
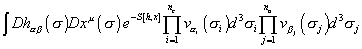
[integral] Dh[alpha] [beta] ([sigma]) Dxu ([sigma]) e-S[x, h] [product series over i to nc] V[alpha]i ([sigma]i) d2 [sigma]i [product series over j to no] V[beta]j ([sigma]j) d2 [sigma]j
where
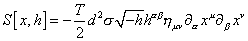
S[x, h] = -(T/2) d2 [sigma] [square root of -h] h[alpha] [beta] n[alpha] [beta] [partial derivative][alpha] xu [partial derivative][beta] xv
and where nc is the number of closed strings, no is the number of open strings, Vαi is a vertex operator that describes emission or absorbtion of a closed string of type αi from the interior of the string world sheet, and Vβj is a vertex operator that describes emission or absorbtion of an open string of type βj from the boundary of the string world sheet. The conformally inequivalent world sheets of a given topology are described by a finite number of parameters. Therefore, these amplitudes can be written as finite-dimensional integrals over these moduli. The dimension of the resulting integral is
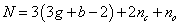
N = 3(3g + b - 2) + 2nc + no
The following defines the Euler beta function.
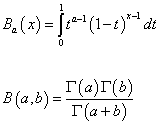
The scattering amplitude is given by
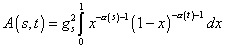
A(s, t) = gs2 [integral from 0 to 1] x-[alpha](s) - 1 (1 - x)-[alpha](t) - 1dx
where the Mandelstam invariants s and t, and the Regge trajectory α(s) are given by
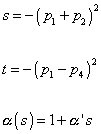
s = -(p1 + p2)2
t = -(p1 - p4)2
[alpha](s) = 1 + [alpha]'s
Mandelstam variables are Lorentz-invariant variables describing the kinematics of particle reactions. Originally the variables were introduced by Mandelstam to describe two-body elastic scattering amplitudes in terms of dispersion relations as functions of two complex variables s and t. Mandelstam variables are also widely used now to describe the kinematics of multibody final states viewed as two incident and two outgoing systems.
Using the Euler beta function, you have
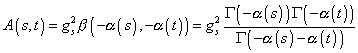
A(s, t) = gs2 B(-[alpha](s), -[alpha](t)) = gs2 (([capital gamma](-[alpha](s)) [capital gamma] (-[alpha](t)))/([capital gamma] (-[alpha](s) – [alpha](t))))
This is called the Veneziano amplitude.