The bosonic string is the first renormalizable theory of gravity, which is a great achievement. However, it is obviously a seriously flawed unrealistic theory. First of all, it contains only bosons with no fermions at all. Second of all, it includes the tachyon. Fortunately, both of these problems can be solved by combining string theory with supersymmetry, resulting in superstring theory. In supersymmetry, you add anticommutators which give rise to fermions. The bosons end up with supersymmetric partners which are fermions, so that way you can get fermions. Also in supersymmetry, the bosonic contributions to the vacuum energy are canceled out by fermionic contributions of identical magnitude and opposite sign. This mechanism is used to cancel out the self-energy contributions to the Higgs mass. As I described, this vacuum energy is the origin of the tachyon. Therefore, supersymmetry allows you to get rid of the tachyon. Therefore, superstring theory contains both bosons and fermions, and no tachyon. An additional benefit of superstring theory is that it reduces the number of dimensions from 26 to 10, so you have fewer extra dimensions to compactify.

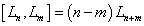
As I said before, the following is the Virasoro algebra.

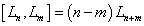
[L_n, L_m] = (n - m)L_{n + m}

The following is the Virasoro algebra with central charges.

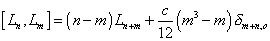
[L_n, L_m] = (n - m)L_{n + m} + (c/12) (m³ - m) [delta]_{m + n, o}

where the second term is the conformal anomaly term, and c is the central charge. The theory has conformal invariance.

In 1971, Pierre Ramond studied solutions to the Dirac equation of the string world sheet. This led to a much larger symmetry algebra than the Virasoro algebra. This new algebra included anticommutating operators, F_n, analogous to the supersymmetry generators Q. This modified Virasoro algebra is

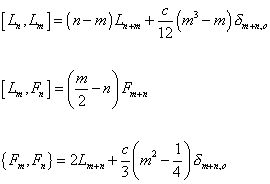
[L_n, L_m] = (n - m)L_{n + m}

[L_m, F_n] = ((m/2) - n) F_{m + n}

{F_m, F_n} = 2L_{m + n} + (c/3) (m² - (1/4)) [delta]_{m + n, o}

This is called the super-Virasoro algebra. This algebra has superconformal invariance.

Also in 1971, John Schwarz and Andre Neveu worked on a bosonic string theory that had an anticommuting field with half integer boundary conditions on the world sheet. They also found a super-Virasoro algebra, although it was slightly different from Ramond's version. Gervais and Sakita determined that the two theories developed by Ramond and by Neveu and Schwarz fit together into two sectors of the same theory, called the RNS formalism. Historically, it was also called the spinning string theory. In this formalism, the supersymmetry is on the two-dimensional world sheet as it propagates through spacetime. A different formalism, developed by Michael Green and John Schwarz in 1981, has the supersymmetry on the 10-dimensional spacetime itself. The second formalism, called the GS formalism, removed any doubt as to whether superstring theory was truly supersymmetric in the traditional sense, and greatly improved the standing and popularity of superstring theory.

In the non-supersymmetric case, you had the following function that describes the world sheet.

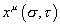
x^u ([sigma], [tau])

where σ parametrizes the position of a point on the string, and τ gives the time evolution. In addition to that, in the supersymmetric case, you also have fermionic partner fields.

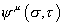
[psi]^u ([sigma], [tau])

x^u transforms as a vector from the 10-dimensional spacetime point of view, and as d scalar fields from the two-dimensional world sheet point of view. ψ^u transforms as a vector from the spacetime point of view, and as a spinor from the world sheet point of view. Together, x^u and ψ^u describe d supersymmetry multiplets, one for each value of u, where u = 0, 1, …d-1, and d is the dimensionality of spacetime.

When you choose a suitable conformal gauge

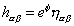
h_{[alpha] [beta]} = e^[phi] n_{[alpha] [beta]}

plus an appropriate fermionic condition, you end up with a world sheet theory that has global supersymmetry with constraints. The constraints form a super-Virasoro algebra. Therefore, in addition to the Virasoro constraints on the bosonic string theory, there are also fermionic constraints.

Remember that for the bosonic string, you had the gauge-fixed action.

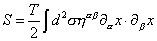
S = (T/2) [integral] d² n^{[alpha] [beta]} [partial derivative]_[alpha] x . [partial derivative]_[beta] x

where T is the tension, and η_{α β} is the two-dimensional Minkowski metric of the flat world sheet. The globally supersymmetric world sheet action that arises in the conformal gauge is

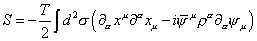
S = -(T/2) [integral] d² [sigma] ([partial derivative]_[alpha] x^u [partial derivative]^[alpha] x_u -i[psi bar]^u p^[alpha] [partial derivative]_[alpha] [psi]_u)

The first term is the same as the bosonic string case, which has the structure of d free scalar fields. The second term is d free massless spinor fields. p^α is two 2 x 2 Dirac matrices, and

is a two-component Majorana spinor.

∂₊

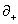
is the derivative with respect to

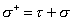
[sigma]⁺ = [tau] + [sigma]

and ∂_-

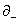
is the derivative with respect to

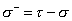
[sigma]^- = [tau] - [sigma]

The Majorana condition means that ψ₊ and ψ_- are real in the representation of the Dirac algebra, which is

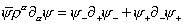
[psi bar] p^[alpha] [partial derivative][alpha] [psi] = [psi]_- [partial derivative]₊ [psi]_- + [psi]₊ [partial derivative]_- [psi]₊

The equations of motion are

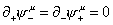
[partial derivative]₊ [psi]_-^u = [partial derivative]_- [psi]₊^u = 0

Therefore, ψ_-^u describes right-movers, and ψ₊^u describes left-movers.

Let's look at the right-movers. The global supersymmetry transformations, which are a symmetry of the gauge-fixed action, are

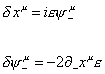
[delta]x^u = i[epsilon] [psi]_-^u

[delta][psi]_-^u = -2[partial derivative]_- x^u [epsilon]

The Virasoro constraint is

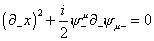
([partial derivative]_- x)² + (i/2) [psi]_-^u [partial derivative]_- [psi]_u- = 0

The first term is the same as for the bosonic string. The second term is an additional fermionic contribution. There is also the fermionic constraint

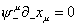
[psi]_-^u [partial derivative]_- x_u = 0

The Fourier modes of these constraints satisfy the super-Virasoro algebra. It's the same for the left-movers.

Let's look at the boundary conditions. The boundary conditions for the bosonic part

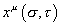
x^u ([sigma], [tau])

are exactly the same as what we did before for the bosonic string, so let's look at the fermionic part

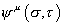
[psi]^u ([sigma], [tau])

You have ψ₊ which describes the left-movers, and ψ_- which describes the right-movers. Now at each end of the open string, the left-movers and right-movers could either be the same, or they could differ by a sign. In other words, you have

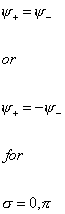
[psi]₊ = [psi]_-

[psi]₊ = -[psi]_-

for

[sigma] = 0, [pi]

Let's say that they are the same at the end of the open string we're calling 0. If they are the same at the 0 end of the open string, you have

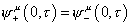
[psi]₊^u (0, [tau]) = [psi]_-^u = (0, [tau])

So at one end of the string, they are the same. Therefore, at the other end, which we call π, they are either the same, or of opposite sign. Therefore, you have two possibilities.

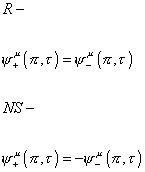
R-

[psi]₊^u ([pi], [tau]) = [psi]_-^u ([pi], [tau])

NS-

[psi]₊^u ([pi], [tau]) = -[psi]_-^u ([pi], [tau])

The first of the above two possibilities is called the Ramond boundary condition, or R. The second possibility is called the Neveu-Schwarz boundary condition, or NS. Sometimes, people call them the Ramond string and the Neveu-Schwarz string. The Ramond string is said to be periodic, and the Neveu-Schwarz string is said to be anti-periodic.

Remember the following equations of motion.

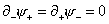
[partial derivative]_- [psi]₊ = [partial derivative]₊ [psi]_- = 0

This allows you to express the general solutions of the boundary conditions as a Fourier series.

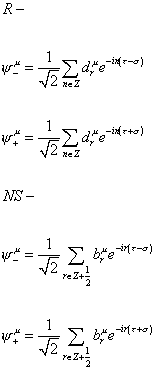
R-

[psi]_-^u = (1/[squareroot of 2]) [summation of n = Z] d_n^u e^{-in([tau] - [sigma])}

[psi]₊^u = (1/[squareroot of 2]) [summation of n = Z] d_n^u e^{-in([tau] + [sigma])}

NS-

[psi]_-^u = (1/[squareroot of 2]) [summation of n = Z + ½ ] b_n^u e^{-in([tau] - [sigma])}

[psi]₊^u = (1/[squareroot of 2]) [summation of n = Z + ½ ] b_n^u e^{-in([tau] + [sigma])}

The Majorana condition implies that

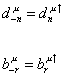
d_-n^u = d_n^u†

b_-r^u = b_r^u†

The index n only has integer values. The index r only has half-integer values. Only the R boundary condition gives a zero mode. You have the following anticommutation relations for the coefficients d_m^u and b_r^u.

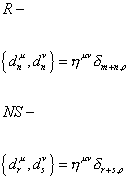
R-

{d_n^u, d_n^v} = [eta]^uv [delta]_{m + n, o}

m, n are contained in Z

NS-

{d_r^u, d_s^v} = [eta]^uv [delta]_{r + s, o}

m, n are contained in Z + ½

Therefore, in addition to the harmonic oscillator operators α_n^u that appear as coefficients in mode expansions of x^u, you also have fermionic oscillator operators d_n^u and b_r^u that appear in mode expansions of ψ^u.

The basic structure {b, b^†} = 1 describes a two-state system with b | 0 > = 0 and b^† | 0 > = | 1>. The b's and d's with negative indices are raising operators, and those with positive indices are lowering operators. It's basically the same as what we did before for α_n^u.

All the states obtained by acting with the α and b raising operators are bosons. In a simple generalization of the bosonic string, in the NS sector, the ground state satisfies

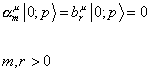
[alpha]_m^u | 0 ; p> = b_r^u | 0 ; p> = 0

m, r > 0

In the R sector, there are zero modes that satisfy the algebra

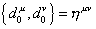
{d₀^u, d₀^v} = [eta]^uv

This is the d-dimensional spacetime Dirac algebra. The d₀'s can then be regarded as Dirac matrices, and all the states in R are spinors. Therefore, all the string states in the NS sector are bosons, and all the string states in the R sector are fermions.

This was the case for the open string. With the closed string, you have both right and left movers at the same time. You have the product of the right and left movers, each of which is the same as the open string spectrum. Therefore, you have four separate sectors in the closed string states. If both the right-movers and left-movers have the same boundary conditions, meaning you have NS x NS or R x R, you have bosons. If they have different boundary conditions, meaning you have NS x R or R x NS, you have fermions.

The zero mode of the fermionic constraint

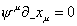
[psi]^u [partial derivative]_- x_u = 0

gives a wave equation for the fermionic strings in the Ramond sector

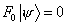
F₀ | [psi] > = 0

called Dirac-Ramond equation, where

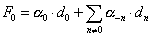
F₀ = [alpha]₀ . d₀ + [summation where n is not 0] [alpha]_-n . d_n

The fermionic ground state | ψ₀ > which satisfies

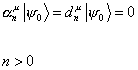
[alpha]_n^u | [psi]₀ > = d_n^u > = 0

n > 0

satisfies the wave equation

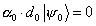
[alpha]₀ . d₀ | [psi]₀ > = 0

The action for the string in the conformal gauge is

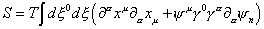
S = T [integral] d[xi]⁰ d[xi]¹ ([partial derivative]^[alpha] x^u [partial derivative]_[alpha] x_u + [psi]^u [gamma]⁰ [gamma]^[alpha] [partial derivative]_[alpha] [psi]_n)

where α = 0, 1 are the world sheet coordinates, and ψ^u are two-dimensional Hermitian forms. The γ's are given by

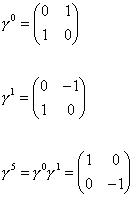
using

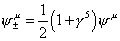
[psi]_±^u = ½ (1 + [gamma]⁵) [psi]^u

the fermionic part of the Lagrangian can be written as

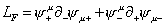
L_F = [psi]₊^u [psi]_u+ + [psi]_-^u [partial derivative]₊ [psi]_u-

The field equations that follow from L_F are

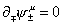
[partial derivative]_-/+ [psi]_±^u = 0

ψ₊ is only a function of ξ₊, and ψ_- is a function of ξ_-. The Fourier expansion of ψ_±^u is

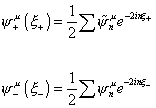
[psi]₊^u ([xi]₊) = ½ [summation] [psi tilda]_n^u e^-2in[xi]₊

[psi]_-^u ([xi]₊) = ½ [summation] [psi]_n^u e^-2in[xi]_-

For the Ramond string, n takes integer values, and for the Neveu-Schwarz string, n takes half-integer values. Therefore, for the NS case, you have

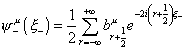
[psi]_-^u ([xi]_-) = ½ [summation of r from -infinity to infinity] b_{r + ½}^u e^{-2i (r + ½)[xi]_-}

and in the R case, you have

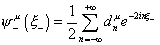
[psi]_-^u ([xi]_-) = ½ [summation of n from -infinity to infinity] d_n e^-2in[xi]_-

Now, let's look at the vacuum state | 0 >, the one particle state b_{- ½} | 0>, etc. where it goes over d - 2 transverse dimensions, with i = 2, 3, …d - 1. For the Ramond string, you have

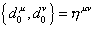
{d₀^u, d₀^v} = [eta]^uv

This is the Clifford algebra, and has a 2^d/2 dimensional representation in the ground state. Therefore, the ground state must transform as a spinor representation of the Lorentz group. Only the fermions transform according the spinor representation of the Lorentz group. Therefore, the Ramond string must lead to fermions, unlike the bosonic string or the Neveu-Schwarz string which lead to bosons.

Now let's evaluate the world sheet energy-momentum tensor T_αβ, and obtain its Fourier coefficients.

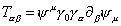
T_{[alpha][beta]} = [psi]^u [gamma]₀ [gamma]_[alpha] [partial derivative]_[beta] [psi]_u

From this you get

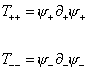
T₊₊ = [psi]₊ [partial derivative]₊ [psi]₊

T_-- = [psi]_- [partial derivative]₊ [psi]_-

The fermionic contribution to L₀ for NS is

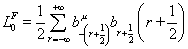
L₀^F = ½ [summation over r from -infinity to infinity] b_{-(r + ½)}^u b_{r + ½} (r + ½)

and for R is

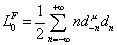
L₀^F = ½ [summation over n from-infinity to infinity] nd_-n^u d_n

The vacuum energy for the Neveu-Schwarz case is

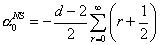
[alpha]₀^NS = -((d - 2)/2) [summation over r from 0 to infinity] (r + ½)

The first excited state is

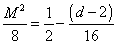
M²/8 = ½ - (d - 2)/16

Since there are not enough components of this state to form an irreducible representation of the SO(d - 2) group, this state must have zero mass. So if M = 0, then d = 10.

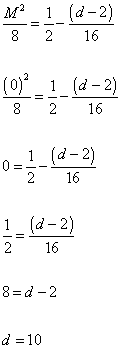
M²/8 = ½ - (d - 2)/16

( 0 )²/8 = ½ - (d - 2)/16

0 = ½ - (d - 2)/16

½ = (d - 2)/16

8 = d - 2

d = 10

Therefore, the inclusion of Neveu-Schwarz string reduces the critical dimension from 26 to 10. Therefore, superstrings exist in ten spacetime dimensions.

You have the total number of spacetime dimensions. One of the dimensions is time. One is the longitudinal direction of a particle traveling through it. So for d = 4, which is normal spacetime, you have two transverse directions. The bosonic string requires d = 26, which has 24 transverse directions. Superstring theory requires d = 10, which has eight transverse directions.

With the bosonic string, you only had the α oscillators. Each α contributes -1/24 to the normal ordering constant, for each transverse direction. In the bosonic string, you have 24 transverse directions so

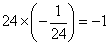
24 x (-1/24) = -1

so the bosonic string theory has a normal ordering constant of -1, and therefore has the mass formula

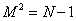
M² = N -1

With superstrings, you have both the α oscillators and the b oscillators. The α oscillators contribute -1/24 to the normal ordering constant, as before, and in addition, the b oscillators each contribute -1/48 to the normal ordering constant. In superstring theory, you have eight transverse directions so you have

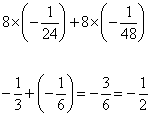
8 x (-1/24) + 8 x (-1/48)

-1/3 + (-1/6) = -3/6 = -1/2

so superstring theory has a normal ordering constant of -½, and therefore has the mass formula

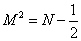
M² = N - ½

To repeat, the mass formula for the bosonic string is

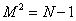
M² = N - 1

In the lowest state, N = 0, so you have

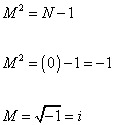
M² = ( 0 ) -1 = -1

M = [squareroot of -1] = i

so therefore you have a tachyon which is an impossible particle. The mass formula for the superstring is

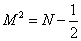
M² = N - ½

In the lowest state, N = 0, so you have

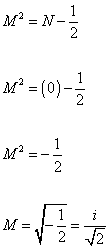
M² = ( 0 ) - ½

M² = -½

M = [squareroot of -½] = i/[squareroot of 2]

so you still have a tachyon which creates an unstable vacuum. Therefore, as of now, superstring theory still contains a tachyon in the spectrum. However, with superstring theory, there exists a way to get rid of it which did not exist for the bosonic string. This is achieved by using the GSO projection, which was developed by Ferdinando Gliozzi, Joel Sherk, and David Olive in 1976.

The GSO projection is a truncation in the NS sector, where you keep the states with an odd number of b oscillator excitations, and remove the states with an even number of b oscillator excitations. When you do this, N can take only half-integer values. The mass formula is the same

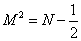
M² = N - ½

except now, the lowest value of N is not zero but ½. Therefore, you have

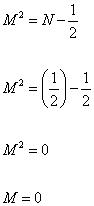
M² = ( ½ ) - ½

M² = 0

M = 0

Therefore, you don't have a tachyon. You could not have done this with the bosonic string since there are no b oscillators to manipulate. The possible values for M² are

M² = 0, 1, 2,…

The GSO projection also acts on the R sector where there is an analogous restriction on the d oscillators. This imposes a chirality projection on the spinors.

Let's look at the massless spectrum of the GSO projected theory. The ground state is a massless boson represented by the state

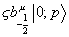
[zeta] b_-½^u | 0 ; p>

which has d - 2 = (10) - 2 = 8 physical polarizations. The ground state fermion is a massless Majorana-Weyl fermion which has 8 physical polarizations.

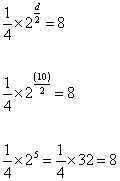
¼ x 2^d/2 = 8

¼ x 2^(10)/2 = 8

¼ x 2⁵ = ¼ x 32 = 32/4 = 8

Therefore, the ground state boson and the ground state fermion both have the same number of physical polarizations as required by a supersymmetry theory. You have equal numbers of bosons and fermions as required by a theory with spacetime supersymmetry. This is a pair of fields that enter into the 10-dimensional Yang-Mills theory. You have an equal number of bosons and fermions at every mass level. Therefore, the superstring theory has full spacetime supersymmetry.

For the bosonic string, the generating function is

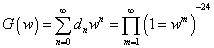
G(w) = [summation over n from 0 to infinity] d_n wⁿ = [product series over m from 1 to infinity] (1 - w^m)^-24

where d_n is the number of physical states with

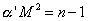
[alpha]' M² = n - 1

and

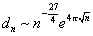
d_n ~ n^-27/4 e^{4[pi][squareroot of n]}

Let's say d_NS ( n ) is the number of bosonic states with M² = n, and d_R ( n ) is the number of fermionic states with M² = n. Then the generating functions for the Neveu-Schwarz string and the Ramond string are

f_NS(w) = [summation over n from 0 to infinity] d_NS (n) wⁿ = (1/(2[squareroot of w])) ([product series of m from 1 to infinity] ((1 + w^{m - ½})/(1 - w^m))² - [product series of m from 1 to infinity]((1-w^{m - ½})/(1 - w^m))⁸)

f_R(w) = [summation over n from 0 to infinity] d_R (n) wⁿ = 8[product series of m from 1 to infinity]((1 + w^m)/(1 = w^m))⁸

The 8's in the exponents refer to the number of transverse directions in ten dimensions. The GSO projection causes the subtraction of the second term in f_NS, and the reduction of the coefficient in f_R from 16 to 8.

Before using the GSO projection, the allowed states for the Neveu-Schwarz string include

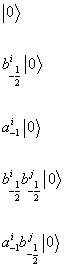
| 0 >

b_-½ⁱ | 0 >

a_-1ⁱ | 0 >

b_-½ⁱb_-½^j | 0>

a_-1ⁱb_-½ⁱ

| 0>

After using the GSO projection, the only allowed states are

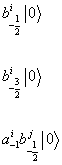
b_-½ | 0 >

b_-3/2ⁱ | 0 >

a_-1ⁱ b_-½^j | 0 >

For a closed string, all the points on the string are the same, and are therefore invariant under the shift

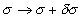
[sigma] -> [sigma] + [delta] [sigma]

The unitary operator for the shift is

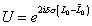
U = e^{2i[delta][sigma](L₀ - [L tilda]₀)}

For it to be invariant, U = 1, which is only true if

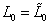
L₀ = [L tilda]₀

which means the allowed energy levels are those for which the right-movers and left-movers have the same mass. The massless states are

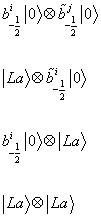
b_-½ⁱ | 0 > x [b tilda]_-½^j | 0>

| La > x [b tilda]_-½ | 0 > x | La >

| La > x | La >

The first one gives the graviton, h^ij = h^ij, the antisymmetric field, b^ij = -b^ji, and the dilaton, φ. The next two give rise to the gravitino and the dilatino. The last one gives rise to a set of 64 scalar bosons.

Now, let's look at the five superstring theories, which are Type I, Type IIA, Type IIB, Heterotic SO(32), and Heterotic E₈ x E₈. Type I superstring theory has N = 1 supersymmetry, and therefore has 16 supercharges. It has unoriented closed and open strings. It is the only superstring theory with open strings. It has a Yang-Mills gauge group, which at the classical level, could be any SO(n) or Sp(n) group, for any value of n. However, when you take quantum effects into account, you have to choose a value for which the anomalies cancel. Quantum consistency requires that the gauge group be SO(32). For Type I superstrings, the SO(32) gauge quantum numbers are carried by the endpoints of the open strings. For the other string theories, the gauge quantum numbers are carried by the string itself. The SO(32) Yang-Mills gauge group is specifically on the open strings, so the spin-1 gauge bosons are on the open strings. The graviton is on the closed strings. Including both the open and closed strings, Type I superstring theory has spin-1 gauge bosons, the graviton, and fermions.