In the section on the bosonic string, I explained how the closed string states are the tensor product of the two open string states. You can do the same thing here, forming a closed string spectrum that is a tensor product of the two supersymmetric string states. Each consists of a vector and a Majorana-Weyl spinor. Therefore, you have a tensor product of a vector and a Majorana-Weyl spinor, and another vector and Majorana-Weyl spinor.
(vector + MW spinor) x (vector + MW spinor)
Now, the two spinors could have either same or opposite chirality. When the two spinors have opposite chirality, you have Type IIA superstring theory. When the two spinors have the same chirality, you have Type IIB superstring theory. With Type IIA superstring theory, the massless spectrum forms the Type IIA supergravity multiplets. Since the two spinors have opposite chirality, they cancel each other out. This means that the resulting theory is left-right symmetric, or parity conserving. Since the real world is parity violating, this was initially considered strong evidence against Type IIA superstring theory. However, later it was figured out how to induce parity violation through the compactification process. If the two MW spinors have the same chirality, they re-enforce each other. Therefore, Type IIB superstring theory is chiral, or parity-violating.
Type IIA and Type IIB superstring theory have a vector x spinor and spinor x vector which are the gauge fields for the local supersymmetry. From this, you get two gravitinos. In four spacetime dimensions, gravitinos are spin 3/2, although the situation is more complicated in 10 spacetime dimensions. Since the Type II string theories have two gravitinos, they therefore have N = 2 supersymmetry. The supersymmetry charges are Majorana-Weyl spinors, which have 16 components, so the Type II theories have 32 conserved supercharges. This is the same amount of supersymmetry as N = 8 supersymmetry in four spacetime dimensions. Type II strings are also related to a type of bosonic string called Type 0.
Now, there is what originally appeared to be a major drawback to Type IIA and Type IIB superstring theories. Although in the bosonic string theory, you have bosons on closed strings, with superstrings, the Yang-Mills gauge groups, and thus the gauge bosons are only on open strings. Since Type IIA and Type IIB string theories have only closed strings, the string states don't give rise to bosons, except of course for the graviton which is intrinsic in all closed strings. Therefore, these theories, in their original simple form, have half-integer spin particles, which are the fermions, and a spin-2 particle, which is the graviton, but no spin-1 particles, such as the photon. Since there are no gauge bosons, there is no gauge symmetry at all. However, later it was figured out a way to compactify the extra dimensions in such a way so that the compactification process itself gives rise to gauge bosons, and fermions charged under gauge interactions. This is another example of how the extra dimensions of string theory turned out to be a blessing in disguise since in the process of compactifying the extra dimensions, you can get rid of many of the problems in string theory, and arrive at a much more realistic theory of nature.
However, when the Type IIA and Type IIB superstring theories were first discovered, or invented, it was thought that they only had fermions with no bosons. Meanwhile, the bosonic string theory had only bosons but no fermions. If you could only combine these two closed string theories together, you could get a closed string theory with both bosons and fermions. This is the motivation behind the two heterotic string theories developed by D. Gross, J. Harvey, E. Martinez, and R. Rohm in 1985. On a closed string, the left-movers and right-movers operate totally independently of each other. What if the left-movers were non-supersymmetric, and the right-movers were supersymmetric? Then you could get one closed string that gives rise to both gauge bosons and fermions, as well as the graviton. The most obvious difficulty in having both non-supersymmetric and supersymmetric states on the same string is that the non-supersymmetric states exist in 26 dimensions, and the supersymmetric states exist in 10 dimensions. The solution is to initially compactify the extra 16 dimensions of the left-mover states on a torus, so they will both have 10 dimensions. Later, you can compactify six of those ten dimensions on another manifold to give rise to the familiar four spacetime dimensions. When you compactify the 16 extra dimensions on a torus, it gives rise to a local internal symmetry group of rank 16. It turns out that there are only two consistent possibilities for this group which are SO(32), same as the SO(32) group of Type I string theory, and E8 x E8. Therefore, there are two heterotic string theories, which are Heterotic SO(32) and Heterotic E8 x E8.
The real world is parity violating, so you would want a theory that is parity violating, unlike the Type IIA string theory that is parity conserving. However, if your theory is parity violating, you have the problem of chiral anomalies. Chiral gauge theories can be inconsistent due to chiral anomalies. This happens when you have a quantum mechanical breakdown of the gauge symmetry due to certain one-loop Feynman diagrams. The trick then is to choose a theory where the chiral anomalies cancel each other out so you end up with no anomalies in the resulting theory. In four spacetime dimensions, the offending diagrams are triangles. This is called the Adler-Bell-Jackiw anomaly, discovered by Steve Adler, and independently by John Bell and Roman Jackiw.

In the Standard Model, all of the chiral anomalies cancel each other out. In ten dimensional gauge fields, the anomalous Feynman diagrams are hexagons.
You should choose a theory in which the anomalies cancel each other out. Here are some possible theories.
1. N = 1 supersymmetric Yang Mills theory-
This is the theory for the open strings in Type I superstring theory. This theory has anomalies that do not cancel out.
2. Type I supergravity -
This is the theory for the closed strings in Type I superstring theory. This theory has anomalies that do not cancel out.
3. Type IIA supergravity -
This is the theory for Type IIA superstrings. Since the theory is non-chiral, it therefore can't have chiral anomalies.
4. Type IIB supergravity -
This is the theory for Type IIB superstrings. This theory has three chiral fields, each of whom contribute anomalies. However, in 1983, Edward Witten and Alvarez-Gaume proved that all the anomalies cancel.
5. Type I supergravity coupled to supersymmetric Yang-Mills -
This is the theory of the two heterotic superstrings. This theory has anomalies for every choice of Yang-Mills gauge group except SO(32) and E8 x E8. The theory has anomalies but all the anomalies cancel if and only if the gauge group is either SO(32) or E8 x E8. This was proved by John Schwarz and Michael Green in 1984. This mechanism is called the Green-Schwarz anomaly cancellation mechanism.
Therefore, at one time, the two heterotic string theories really seemed to be our best hope, since in Type I string theory, the anomalies don't cancel, and in Type IIA and Type IIB, there did not seem to be any spin-1 gauge bosons. The two Lie group SO(32) and E8 x E8 have several properties in common. They are both rank 16, and are 496-dimensional. Their weight lattices correspond to the only two even self-dual lattices in 16 dimensions. Remember that the heterotic strings have 26-dimensional left-movers, and 10-dimensional right-movers. The extra 16 dimensions of the left-movers are associated with an even self-dual 16-dimensional lattice. In this way, you can build in the SO(32) or E8 x E8 gauge symmetry.
The left-movers are bosonic, and thus have 26 dimensions, or 24 transverse directions, or 24 degrees of freedom. Of these, 16 are compactified coordinates. One bosonic degree of freedom is equivalent to two Majorana fermions. Therefore, the left-movers have 8 bosonic coordinates, and 32 fermionic coordinates. If all 32 fermions have the same boundary conditions, the gauge group will be SO(32). If 16 of the fermions have the same boundary conditions, you end up with E8 x E8.
For the SO(32) case, the states with zero mass are
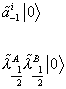
[alpha tilda]-1i | 0 >
[lambda tilda]-½A [lambda tilda]-½B | 0 >
The physical particle spectrum is
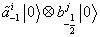
[alpha tilda]-1i | 0 > x b-½j | 0 >
which is the graviton, hij, an antisymmetric field, bij, and the dilaton, φ
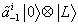
[alpha tilda]-1i | 0 > x L
which is the gravitino and the dilatino
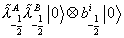
[lambda tilda]-½A [lambda tilda]-½B | 0 > x b-½j | 0 >
which is the gauge bosons
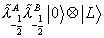
[lambda tilda]-½A [lambda tilda]-½B | 0 > x | L >
which is the gaugino.
The resulting low energy theory is a 10-dimensional N = 1 supergravity with an SO(32) Yang-Mills group.
For the E8 x E8 case, you have
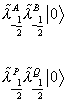
[lambda tilda]-½A [lambda]-½ | 0 >
[lambda tilda]-½P [lambda tilda]-½Q | 0 >
The massless states are the Ramond vacuum which is a spinor under SO(16) which is 128-dimensional. This has two massless states. Adding these, you get in the A-sector, 120 + 128 = 248-dimensional representation, which is the adjoint representation of E8. You have the same thing in the P-sector where you get another 248-dimensional representation of another E8, leading E8 x E8 as the gauge group. Combining with the right-movers, you get a 10-dimensional N = 1 supergravity theory coupled with the E8 x E8 Yang-Mills group.
Here is the Lagrangian for the Heterotic E8 x E8 superstring theory.
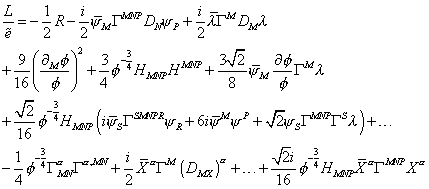
L/[e tilda] = -½R - (i/2) [psi bar]m [capital gamma]MNP DN [psi]P + (i/2) [lambda bar] [capital gamma]M DM [lambda] + (9/16) (([partial derivative]M [phi])/[phi])2 + (3/4) [phi]-3/2 HMND HMND + (3[squareroot of 2]/8) [psi bar]M (([partial derivative][phi])/[phi]) [capital gamma]M [lambda] + ([squareroot of 2]/16) [phi]-3/4 HMNP (I[psi bar]S [capital gamma]SMNPR [psi]R + 6i[psi bar]M [psi]P + [squareroot of 2] [psi]S [capital gamma]MNP [capital gamma]S [lambda]) + …-¼[phi]-3/4 [capital gamma]MN[alpha] [capital gamma][alpha], MN + i/2 [X bar][alpha] [capital gamma]M (DMX)[alpha] + …+([squareroot of 2]i/16) phi]-3/4 HMNP [X bar][alpha] [capital gamma]MNP X[alpha]
where
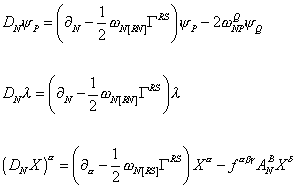
DN [psi]P = ([partial derivative]N - ½wN[RS] [capital gamma]RS) [psi]P - 2wNPQ [psi]Q
DN [lambda] = ([partial derivative]N - ([partial derivative]N - ½wN[RS] [capital gamma]RS)[lambda]
(DNX)[alpha] = ([partial derivative]N - ½wN[RS] [capital gamma]RS)X[alpha] -f[alpha][beta][delta] ANBX[delta]
The Yang-Mills strength is
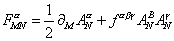
FMN = ½[partial derivative]M AN[alpha] + f[alpha][beta][delta] AMBAN[gamma]
fαβγ are the fine structure constants of the group
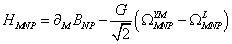
HMNP = [partial derivative]M BNP - (G/[squareroot of 2]) ([omega]MNPYM - [omega]MNPL)
where G is the gravitational constant. The Yang-Mills Chern-Simons form is
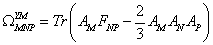
[omega]MNPYM = Tr(AMFNP - (3/2)AMANAP)
the Lorentz Chern-Simons form is
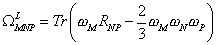
[omega]MNPL = Tr(wM RNP - (2/3) wMwNwR)
and ψM is the gravitino, φ is the dilaton, λ is the dilatino, AMα is the gauge boson, Xα is the gaugino, and α is the E8 x E8 index. eMA is the zweibein, which is the two-dimensional version of the vielbein, referring to the two-dimensional world sheet. The geometry of a manifold is completely described in any coordinate patch by a set of orthogonal unit vectors called the vielbein, frame, or tetrad.
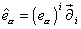
[e hat][alpha] = (e[alpha])i [partial derivative]i
where
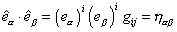
[e hat][alpha] . [e hat][beta] = (e[alpha])i (e[beta])i gij = [eta][alpha][beta]
and where
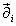
[partial derivative]i
is the coordinate basis vector, gij is the metric, and ηαβ is Minkowski spacetime. In any given number of dimensions, you take the German word for that number, and "bein", which means "leg", and that's the name for the vielbein for that number of dimensions. Thus, a two-dimensional vielbein is called a zweibein. An n-dimensional vielbein is a set of n orthonormal basis vectors defined over the manifold. Vielbein is German for “many legs”, einbein is "one leg", zweibein, is “two legs”, dreibein is “three legs”, vierbein is “four legs”, funfbein is "five legs", elfbein is "eleven legs", etc.
As I mentioned earlier, T-duality relates string theories by the following relation.
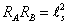
RA RB = ls2
where A and B are the two string theories, RA is the radius of the circle that one of the extra dimensions of A is compactified on, RB is the radius of the circle that one of the extra dimensions of B is compactified on, and ls is the string length, where l is lower case "L". Let's use dimensions where ls = 1, so you have
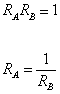
RA RB = 1
RA = 1/RB
There are two types of excitations that a string can have. One is Kaluza-Klein excitations, which exist in any quantum field theory. The other is winding mode excitations which only exist for strings. It turns out that T-duality also relates these two types of excitations for two string theories.
In the context of string theory, Kaluza-Klein excitations exist because in order for the wave function eipx to be single valued, the momentum along the circle must be a multiple of 1/R.
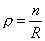
p = n/R
where p is the momentum, R is the radius of the circle, and n is an integer. From the point of view of four-dimensional spacetime, this contributes
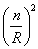
(n/R)2
to the square of the mass, which is the same as the square of the energy.
Winding mode excitations exist because a closed string can wind m times around the circular dimension. Imagine you are wrapping a rubber band around a pencil. This makes the following contribution to the energy.
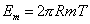
Em = 2[pi]RmT
If we are using units where the string length ls = 1, then
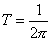
T = 1/(2[pi])
so
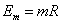
Em = mR
The combined energy squared of the Kaluza-Klein and winding mode excitations is
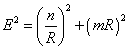
E2 = (n/R)2 + (mR)2
To this, you could also add the string oscillator contributions. If you have two string theories related by T-duality, and you exchange both m and n, as well as R and 1/R, it leaves the energy invariant.
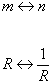
m <-> n
R <-> 1/R
Together these two interchanges leave the energy invariant. This means that what is interpreted as a Kaluza-Klein excitation in one string theory is interpreted as a winding mode excitation in the T-dual theory, where the radius of the compactified dimension of the first theory is R, and of the second theory is 1/R.
One implication is that the usual geometric concepts break down at short distances, and classical geometry is replaced by quantum geometry, which is described mathematically by 2D conformal field theory. This also predicts a generalization of the Heisenberg Uncertainty Principle. According to this, Δx would be bounded below not just by 1/Δp but also by the string length, ls. However, if you include non-perturbative effects, it might push this lower bound down to the Planck length.
Type IIA and IIB string theory are related by T-duality. The two heterotic string theories are also related by T-duality. In that case, one heterotic string has the SO(32) gauge group, and the other has E8 x E8. Therefore, you have to relate the two gauge groups. When the compactification on a circle is carried out, you have to include effects called Wilson lines. These break the gauge groups to SO(16) x SO(16) which is the common subgroup of SO(32) and E8 x E8.
To understand how superstring theory can produce the correct details of familiar traditional particle physics, you have to know about how the extra dimensions are compactified on a Calabi-Yau manifold. However, in order to just explain what a Calabi-Yau manifold actually is, I have to try to very briefly explain some advanced concepts in algebraic topology, which is a very complicated subject.
In 1943, Shiing-Shen Chern worked on characteristic classes and fiber bundles. In 1954, Eugenio Calabi conjectured the existence of a Kahler manifold with a Ricci-flat metric with a vanishing first Chern class, and a given complex structure and Kahler class. In 1976, Shing-Tung Yau proved the Calabi conjecture, and discovers Calabi-Yau space. In 1985, Candelas, Strominger, Horowitz, and Witten proposed using Calabi-Yau manifolds for the extra dimensions in heterotic string theory.
Projective geometry was essentially invented by Renaissance painters. Real projective space is RPn. Points in RPn are 1-dimensional subspaces of Rn+1, and are lines through the origin in Euclidean space. Complex projective space is CPn. The Fubini-Study metric is the metric on complex projective space that has the maximal amount of symmetry.
A Calabi-Yau manifold can be generalized to any number of dimensions, but it's usually described as having three complex dimensions. Since their complex structure may vary, you can think of them as having six real dimensions and a fixed smooth structure. A Calabi-Yau manifold has a non-vanishing harmonic spinor φ, which means that its canonical bundle is trivial.
The wedge product is the product of an exterior algebra, also called an alternating algebra or Grassmann algebra. If α and β are differential k-forms of degrees p and q respectively, then
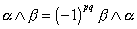
[alpha] /\ [beta] = (-1)pq [beta] /\ [alpha]
It is not in general commutative but it is associative and bilinear.
Let's say in R6, you have the coordinates x1, x2, x3 , and y1, y2, y3 so that
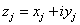
zj = xj + iyj
gives it the structure of C3. Then
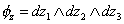
[phi]2 = dz1 /\ dz2 /\ dz3
is a local section of the canonical bundle. A unitary change of coordinates w = Az, where A is a unitary matrix, transforms φ by det A.

[phi]w = det A [phi]z
If the linear transformation A has determinant 1, meaning it is a special unitary transformation, then φ is defined as φz or φw. On a Calabi-Yau manifold, such a φ can be defined globally.
On a Riemannian manifold M, tangent vectors can be moved along a path by parallel transport. Think of the diagram in my paper on tensors. A closed loop at a base point p gives rise to an invertible linear map of TMp, the tangent vectors at p. It is possible to compare closed loops by following one after another, and to invert them by going backwards. Therefore, a set of linear transformations arising from parallel transport along closed loops is a group called a holonomy group. Since parallel transport preserves the Riemannian metric, the holonomy group is contained in the orthogonal group O(n). If the manifold is orientable, then it is contained in the special orthogonal group. A generic Riemannian metric on an orientable manifold has a holonomy group of SO(n). Here are some Riemannian manifolds and their holonomy groups.
Kahler manifold (2n-dimensional) - U(n)
Calabi-Yau manifold (2n-dimensional) - SU(n)
hyper-Kahler manifold (4n-dimensional) - Sp(n)
quaternion Kahler manifold (4n-dimensional) - Sp(n) Sp(1)
Joyce manifold (7-dimensional) - G2
One definition of a Calabi-Yau manifold, based on Riemannian geometry, is that it is a 2n-dimensional manifold whose holonomy group reduces to SU(n). Therefore, if n = 3, the Calabi-Yau manifold is a 6-dimensional manifold whose holonomy group reduces to SU(3).
Another definition of a Calabi-Yau manifold is that it is a calibrated manifold with a calibration form ψ which is algebraically the same as the real part of

dz1 /\ dz2 /\…/\ dzn
Another definition of a Calabi-Yau manifold is that it is a Kahler manifold with vanishing Chern class. A Kahler manifold is a complex manifold for which the exterior derivative of the fundamental form Ω associated with a given Hermitian metric vanishes so dΩ = 0. In other words, it is a complex manifold with a Kahler structure. It has a Kahler form so it is also a sympletic manifold. It has a Kahler structure so it is a Riemannian manifold. A Kahler structure on a complex manifold combines a Riemannian metric of the underlying real manifold with a complex structure. A Kahler metric is defined such that near any point p, there exist holomorphic coordinates zk = xk + iyk such that the metric has the form
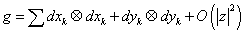
g = [summation] dxk x dxk + dyk x dyk + O(| z |2)
A Chern class is a gadget defined for complex vector bundles. The Chern classes of a complex manifold are the Chern classes of its tangent bundle. The ith Chern class is an obstruction to the existence of (n - i + 1) complex linearly independent vector fields on that vector bundle. The ith Chern class is in the (2i)th cohomology group of the base space. For any collection of Chern classes such that their cup product has the same dimension as the manifold, this cup product can be evaluated on the manifold's fundamental class. The resulting number is called the Chern number for that combination of Chern classes. Chern numbers are cobordism invariant. The fundamental class is the canonical generator of the nonvanishing homology group on a topological manifold. The cup product is a product on cohomology classes. Cobordism is where the union of two manifolds is the boundary of a compact (n + 1)-manifold. So to repeat, a Calabi-Yau manifold is a Kahler manifold with vanishing Chern class.
Calabi-Yau manifolds, as well as their moduli spaces, have many interesting properties, such as the symmetries in the numbers forming the Hodge diamond of a compact Calabi-Yau manifold. These symmetries, called mirror symmetries, also exist for another Calabi-Yau manifold which is a mirror of the first Calabi-Yau manifold. With mirror symmetry, two topologically distinct Calabi-Yau compactifications in string theory can give rise to identical models of particle physics. Calabi-Yau manifolds are also related to Kummer surfaces.
Let's say you have a real manifold of dimension n. You can define the p-forms Ap, where p = 1, 2,…n, as
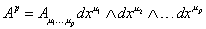
Ap = Au1…updxu1 /\ dxu2 /\ …dxup
where A is antisymmetric in its indices, and /\ is the wedge product which is also antisymmetric.
An exterior derivative of a p-form maps the p-form onto a (p + 1)-form by
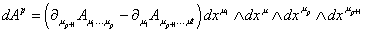
dAp = ([partial derivative]up + 1 Au1…up - [partial derivative]u1 Aup + 1…ut) dxu1 /\ dxu /\ dxup /\ dxup + 1
A p-form is closed if dAp = 0. A p-form is exact if Ap = dAp - 1. Since d2 = 0, an exact form is closed. If two closed forms differ by an exact form, they are in the same equivalence class. The collection of closed p-forms is called the cohomology group Hp. The number of different independent equivalence classes of p-forms is called the Betti number, bp, and is the dimension of the cohomology group Hp.
The Betti numbers obey the Poincare duality.
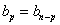
bp = bn - p
where n is the dimension of the manifold. b0 = 1 for any manifold for which bn = 1. The Euler characteristic of a manifold is defined by
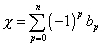
X = [summation over p from 0 to n] (-1)p bp
To study the homology group for a compact manifold of dimension n, you look at all its closed submanifolds. If
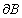
[partial derivative]B
is the boundary of a compact manifold B, then
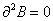
[partial derivative]2 = 0
since a boundary has no boundary. Therefore, the operation ∂ is analogous to the exterior derivative. A p-dimensional closed manifold may or may not be a boundary of a (p + 1)-dimensional closed manifold. If it is a boundary, ignore it. When two p-dimensional submanifolds Mp1 and Mp2 form the boundaries of a (p + 1)-dimensional manifold, they belong to the same equivalence class. Two points on a surface form the boundaries of a line, and therefore belong to the same equivalence class. The number of different equivalence classes gives the dimension of the homology group Hp, and gives the Betti number.
The Hodge decomposition theorem states that for a compact manifold, there is a one-to-one correspondence between a closed form and a harmonic form, which indicates the existence of a zero mode. This correspondence then enables you to obtain the number of massless modes from the Betti numbers.