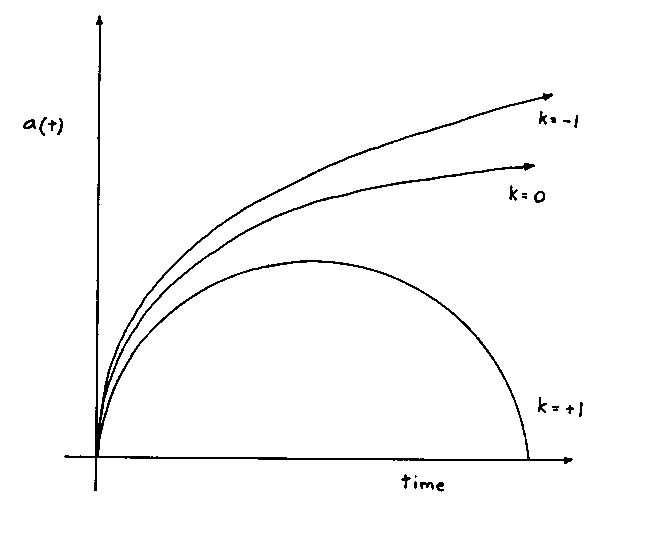
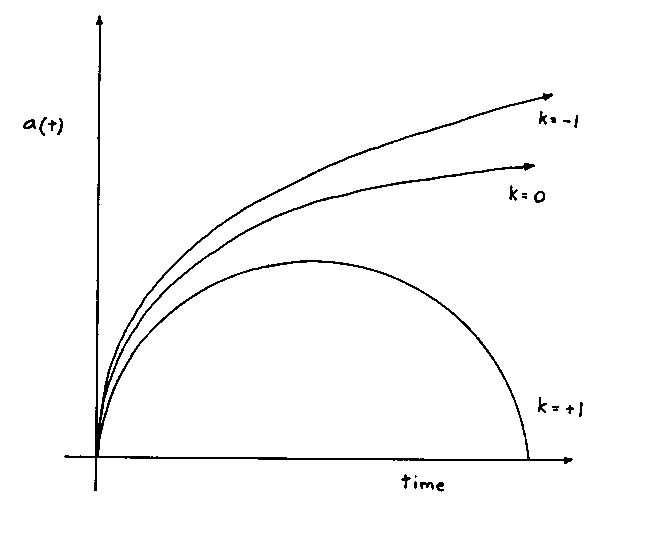
However, remember that this assumes that Λ = 0. With a cosmological constant, you lose the connection between open versus closed, and expand forever versus recollapse. In the real Universe, we have a positive cosmological constant, and so the Universe is spatially flat but the expansion is accelerating.
Now, let’s look at model universes dominated by matter, radiation, and vacuum respectively, and for each one, consider models with k = -1, k = 0, and k = +1.
Matter-dominated, k = -1, open universe

a = (c/2)(cosh φ - 1)
t = (c/2)(sinh φ - φ)
Matter-dominated, k = 0, flat universe

a = (ac/4)1/3 t2/3
Matter-dominated, k = +1, closed universe
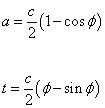
a = (c/2)(1 – cos φ)
t = (c/2)(φ - sin φ)
where φ is the development angle, and is a function of t, and c is a constant defined by
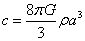
c = (8πG/3) ρ a3
Radiation-dominated, k = -1, open universe
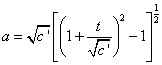
a = [squareroot of c’] [(1 + 1/[squareroot of c’])2 - 1]½
Radiation-dominated, k = 0, flat universe

a = (4c’)1/4 t ½
Radiation-dominated, k = +1, closed universe

a = [squareroot of c’][1 – (1 – t/[squareroot of c’])2]½
where c’ is a different constant defined by
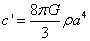
c’ = (8φG/3) ρ a4
For universes dominated by a cosmological constant, you no longer have the connection between open versus closed and expand forever versus recollapse. If Λ is not zero, it could be either positive or negative. If Λ < 0, Ω is negative, and from that, you get
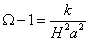
Ω - 1 = k/H2a2
As you see, this can only happen if k = -1. So for Λ , 0, you can only have k = -1.
Vacuum-dominated, Λ < 0, k = -1, open universe
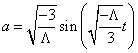
a = [squareroot of (-3/Λ)] sin([squareroot of (-Λ/3)]t)
Vacuum-dominated, Λ > 0, k = -1, open universe

a = [squareroot of (3/Λ)] sinh([squareroot of (Λ/3)]t)
Vacuum-dominated, Λ > 0, k = 0, flat universe

a proportional to e± [squareroot of (Λ/3)]t
Vacuum-dominated, Λ >0, k = +1, closed universe
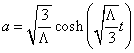
a = [squareroot of (3/Λ)] cosh([squareroot of (Λ/3)]t)
However, it turns out that the last three equations all represent the same spacetime, just in different coordinates. This space, which is the maximally symmetric space with positive cosmological constant, is called de Sitter space. The Λ < 0 solution, which is the maximally symmetric space with negative cosmological constant, and is called anti-de Sitter space.
The deceleration parameter is related to Ω by
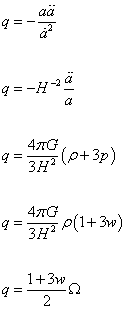
q = -a[a double dot]/[a dot]2
q = -H-2[a double dot]/a
q = 4πG/3H2 (ρ + 3p)
q = 4πG/3H2 ρ(1 + 3w)
q = ((1 + 3w)/2)Ω
Since Ωr is currently negligible, that leaves only two parameters on which Ω depends, Ωm and ΩΛ, which can then be graphed on a 2D graphing system. Here I’m drawing it with Ωm on the horizontal axis, and ΩΛ on the vertical axis, although sometimes you see it reversed.

The horizontal line turns up slightly on the right hand side. Above that line, the universe expands forever. Below that line, it recollapses. The diagonal line Ωm + ΩΛ = 1, going from upper left to lower right, represents a flat universe. To the right of that line, you have a closed universe with positive spatial curvature. To the left of that line, you have an open universe with negative spatial curvature. In the upper left, you have a region of bounce models, where there was no Big Bang, and instead the universe collapsed from infinity, and before reaching a Big Crunch, instead went through a bounce, and expanded again. Universes on the line in the upper left represent loitering models, where they spend a long time close to a constant scale factor. Both bounce models and loitering models have been ruled out. For a while, we thought that our universe had Ωm = 1 and ΩΛ = 0, which is the intersection of the open/closed and expand forever/recollapse lines. However, we now know that the real Universe has Ωm = 0.3 and ΩΛ = 0.7, which corresponds to the X on the diagram.
Working out the conditions for these different possible behaviors is simply a matter of integrating the Friedman equation. Ignoring radiation, the time dependant Hubble parameter is

H2/H02 = ΩΛ(1 – a-2) + Ωm(a-3 - a-2) + a-2
And you look for conditions in which the left-hand side vanishes, defining a turning point in the expansion. Setting the left-hand side to zero gives a cubic equation, and it’s possible to give the conditions under which it has a solution.
Λ < 0 always implies recollapse, which is what you would expect. If Λ > 0 and Ωm < 1, the model always expands to infinity. If Ωm > 1, recollapse is avoided only if
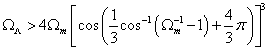
ΩΛ > Ωm[cos((1/3)cos-1(Ωm-1 - 1) + (4/3)π)]3
If Λ is large enough, the stationary point in the expansion is at a < 1, and you have a bounce cosmology. The critical value is

ΩΛ > 4Ωm[f((1/3) f-1(Ωm-1 - 1))]3 where
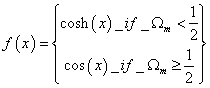
f(x) = cosh(x) if Ωm < ½
f(x) = cos(x) if Ωm ≥ ½
If the universe lies exactly on the critical line, the bounce occurred infinitely long ago, and you have a loitering model. These models were briefly popular in the early 1970’s, when it looked like there was a sharp peak in the quasar redshift distribution, but this turned out to be a mixture of evolution and observational selection.
The same cubic equation that defines the critical conditions for the bounce also gives an inequality for the maximum redshift possible in a bouncing universe, which is that of the bounce

1 + zB ≤ ((1/3)f-1(Ωm-1 - 1))
so bounce models were ruled out once we had seen objects with redshift z > 2.
If k = 0, it’s called an Einstein-de Sitter model. Since Ω = Ωm + ΩΛ = 0.3 + 0.7 = 1 in the real Universe, these models are most relevant to the real universe. The properties of a flat model can usually be obtained by taking the limit Ω -> 1 for either open or closed universes. However, it’s easier to start from the k = 0 Friedman equation.
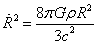
[R dot]2 = (8πGρR2)/3c2
Since both sides are quadratic in R, this makes it clear that the value of R0 is arbitrary unlike models where Ω is not one. The comoving geometry is Euclidean, and there is no natural curvature scale.
You can therefore work in terms of a normalized scale factor a(t), so that the Friedman equation for a universe with matter and radiation but no cosmological constant is

[a dot]2 = H02(Ωma-1 + Ωra-2)
which can be integrated to give the time as a function of scale factor
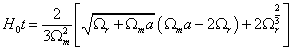
H0t = (2/3Ωm2) [[squareroot of (Ωr + Ωma)](Ωma – 2Ωr) + 2Ωr3/2]
This goes to (2/3)a3/2 for a matter-dominated model, and ½ a2 for a radiation-dominated model. You can also give the model’s dependence on time.
Matter-dominated universe
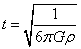
t = [squareroot of (1/(6πGρ))]
Radiation-dominated universe

t = [squareroot of (3/(32πGρ))]
You can also look at a k = 0 model with Ωm + ΩΛ = 1 with radiation negligible, which is the current Universe. This model allows you to retain k = 0, while varying the age of the universe from H0t0 = 2/3 which characterizes the Einstein-de Sitter model.
Ignoring radiation for simplicity, the Friedman equation is
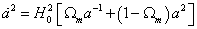
[a dot]2 = H02 [Ωm a-1 + (1 - Ωm) a2)]
and the t(a) relation is
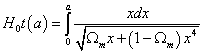
H0t(a) = [integral from 0 to a]xdx/([ΩmX + (1 - Ωm)x4
You then use the substitution
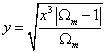
y = [squareroot of ((x3 |Ωm - 1 |)/Ωm]
which turns the integral into
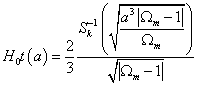
H0t(a) = (2/3) ((Sk-1([squareroot of (a3 | Ωm - 1|)])/Ωm)/[squareroot of (Ωm - 1]))
To make it independent of the current era, you can rewrite the equation as
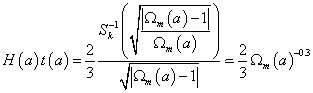
H(a)t(a) = (2/3) ((Sk-1([squareroot of (| Ωm(a) - 1|)])/Ωm)/[squareroot of (Ωm(a) - 1])) ~ (2/3)Ωm(a)-0.3
Up until now, we have been measuring distance with the scale factor a(t). However, of course, in practice, there is no way to measure a(t) directly. In order to relate the theories to the real Universe, you have to express them in terms of quantities that are actually measurable. What you actually observe is the redshift. When you measure light from stars, galaxies, etc., you can measure the tell-tale lines in their atomic spectra. As time goes on, the spectral lines are shifted towards the red end of the spectrum, due to the expansion of the Universe. Imagine a cube containing electromagnetic radiation. As the universe expands, the cube expands, and the electromagnetic radiation gets stretched out.
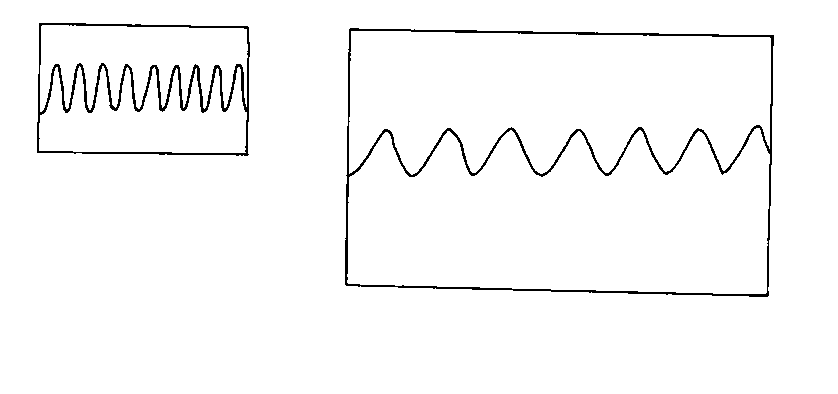
Do you see how the wavelength of the light gets longer, in other words, redshifted? The longer the light has been traveling through space, the longer the length of time since it was emitted, the more the universe has expanded since it was emitted, and so the more the light is redshifted. Therefore, the farther away the source, the more the light is redshifted by the time it reaches us. By measuring the redshift of the light, you can determine how far away the source is. The redshift z is defined as the observed wavelength minus the emitted wavelength, divided by the emitted wavelength, in other words, the fraction the change in the wavelength is of the emitted wavelength. If λ0 is observed wavelength, and λe is emitted wavelength, then

z = (λ0 - λe)/λe
z = (λ0/λe) – 1
λ0/λe = a(t0)/a(te)
z = a(t0)/a(te) – 1
a(t0)/a(te) = z + 1
a(t0) = 1
1/a(te) = z + 1
a(te) = 1/(z + 1)
Therefore, a(t) is equal to 1/(z + 1).
You can also express the redshift z in terms of frequency instead of wavelength.
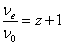
νe/ν0 = z + 1
where νe is emitted frequency, and ν0 is observed frequency. Here is the redshift at matter/radiation equality, when matter and radiation made equal contributions to the energy density of the Universe.
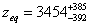
zeg = 3454
Here is the redshift at decoupling, when matter became cool enough for positive ions and electrons to bind into neutral atoms, and so matter decoupled from electromagnetic radiation.

zdec = 1088
Later, due to the first stars, interstellar hydrogen became reionized, so today, most interstellar hydrogen is ionized. Here is the redshift at reionization.
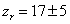
zr = 17 ± 5
You must always keep in mind that redshift can also be caused by the Doppler effect, which is a different phenomenon, so you have

1 + zobs = (1 + zcos)(1 + zdop)
However, usually the cosmological contribution to the redshift can be identified. Here you can relate the density parameter to the age of the universe.
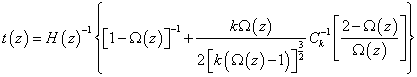
t(z) = H(z)-1{[1- Ω(z)]-1 + (kΩ(z)/2[k(Ω(z) – 1)]3/2) Ck-1[(2 - Ω(z))/Ω(z)]}
where
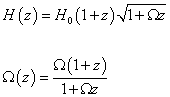
H(z) = H0(1 + z)[squareroot of (1 + Ωz)]
Ω(z) = Ω(1 + z)/(1 + Ωz)
Using

R0 = c/H0 ((Ω - 1)/k)-½
the general relation between commoving distance and redshift is
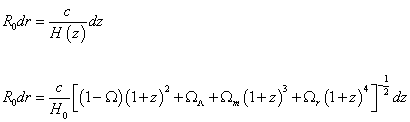
R0dr = (c/H(z))dz
R0dr = (c/H0)[(1 - Ω)(1 + z)2 + ΩΛ + Ωm(1 + z)3 + Ωr(1 + z4)]-½dz
For a matter-dominated Friedman model, this means that the distance to an object from which we receive photons today is
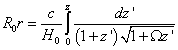
R0r = (c/H0)[integral from 0 to z]dz’/((1 + z’)[squareroot of (1 + Ωz’)])
You can solve the integral using the substitution
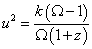
u2 = k(Ω - 1)/Ω(1 + z)
This gives Mattig’s formula, derived by Mattig in 1958.

R0Sk(r) = (2c/H0)((Ωz + (Ω - 2)[[squareroot of (1 + Ωz)] – 1])/(Ω2(1 + z)))
Another version of Mattig’s formula more convenient for a low-density universe is

R0Sk(r) = (c/H0)(z/(1 + z))(1 + [squareroot of (1 + Ωz)] + z)/(1 + [squareroot of (1 + Ωz)] + (Ωz/2))
Also, it can be written in terms of the function Ck(r) instead of Sk(r).

Ck = ((2 - Ω)(2 - Ω + Ωz) + 4(Ω -1) [squareroot of (1 + Ωz)])/(Ω2(1 + z))
You can extend Mattig’s formula to include contributions from both matter, Ωm, and radiation, Ωr.

R0Sk(r) = (2c/H0)(Ωmz + (Ωm + 2Ωr - 2)[[squareroot of (1 + Ωmz + Ωr(z2 + 2z))] – 1])/([ Ωm2 + 4Ωr(Ωr + Ωm - 1)](1 + z))
Unfortunately, there is no equivalent expression that includes vacuum energy, ΩΛ. The second order distance redshift relation depends on the deceleration parameter.
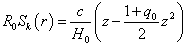
R0Sk(r) = (2c/H0)(z – ((1 + q0)/2)z2)
Since z + 1 is the ratio of the scale factor now and at emission, the redshift will change with time. To calculate the change, differentiate the definition of redshift, and use the Friedman equation. For a matter-dominated model, the result is

[z dot] = H0(1 + z)(1 – [squareroot of (1 + Ωz)])
The redshift is something we can measure. We know the rest frames of the various spectral lines of the electromagnetic radiation from distant galaxies, so we can tell how much their wavelengths have changed from when they were emitted, t1, to when they were observed, t0. Therefore, you know the ratios of the scale factors at these two times. However, we don’t know the times themselves. Since a photon travels at the speed of light, its travel time should be the distance to its source. However, what is the distance to a distant galaxy in an expanding universe? The comoving distance is not measurable, and galaxies need not be comoving in general. In flat space, for a source at distance d, the flux over the luminosity is just one over the area of a sphere centered on the source.
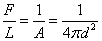
F/L = 1/A = 1/(4πd2)
Using that, you define the luminosity distance as

dL2 = L/4πF
where L is the absolute luminosity of the source, and F is the flux measured by the observer, which is the energy per unit time per unit area. However, in a Friedman-Robertson-Walker universe, the flux will be diluted.
The photons are on average conserved so the total number of photons emitted by the source will eventually pass through a sphere at comoving distance r from the center. Such a sphere is at physical distance d = a0r from the emitter, where a0 is the scale factor when the photons are observed. The flux is diluted by two additional effects. The individual photons redshift by a factor (1 + z), and the photons hit the sphere less frequently since two photons emitted at a time Δt apart will be measured at a time (1 + z)Δt apart. Therefore, you have

F/L = 1/(4πa02r2(1 + z)2)
DL = a0r(1 + z)
You can measure the luminosity distance using standard candles, but r is not measurable so you have to remove that from the equation. On a null geodesic chosen to be radial, you have
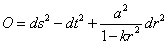
O = ds2 - dt2 + (a2/(1 – kr2))dr2
Which gives

[integral from t1 to t0] dt/a(t) = [integral from 0 to r] dr/[squareroot of (1 – kr2)]
You then expand the scale factor in a Taylor series about its present value.

a(t1) = a0 + ([a dot])0(t1 - t0) + ½([a double dot])0(t1 - t0)2 +…
You can then expand both sides of

[integral from t1 to t0] dt/a(t) = [integral from 0 to r] dr/[squareroot of (1 – kr2)]
to find

r = a0-1[(t0 - t1) + ½H0(t0 - t1)2 + …]
Using
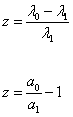
z = (λ0 - λ1)/&lambda1
z = a0/a1 - 1 The Taylor expansion is the same as
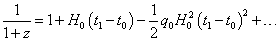
1/(1 + z) = 1 + H0(t1 - t0) – ½q0H02(t1 - t0)2 + …
For small H0(t1 - t0), this can be inverted to give

t0 - t1 = H0-1[z – (1 + q0/2)z2 + …]
substituting into

r = a0-1[(0 - t1) + ½H0(0 - t1)2 + …]
gives you

r = (1/a0H0) [z – ½(1 + q0)z2 + …]
Then using
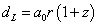
dL = a0r(1 + z)
you have

dL = H-1[z + ½(1 – q0)z2 + …]
which is another way of writing Hubble’s Law, v = Hd
If you write the Robertson-Walker metric in the following form
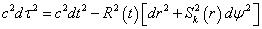
c2dτ2 = c2dt2 - R2(t) [dr2 + Sk2 (r)dψ2]
then the comoving volume is

dV = 4π [R0 Sk(r)]2 R0dr
The proper transverse size of an object seen by us is its comoving size dψSk(r) times the scale factor at the time of emission.

dl = dψR0Sk(r)/(1 + z)
In order to get the relation between monochromatic flux density and luminosity, you start by assuming isotropic emission, so that photons emitted by the source pass with uniform flux density through any sphere centered on the source. You are free to shift the origin, and consider the Robertson-Walker metric as centered on the source. The photons are then passing through a sphere, where we are located on the surface of the sphere, that has a proper surface area
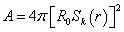
A = 4π[R0Sk(r)]2
However, the photon energies and arrival times are redshifted, reducing the flux by a factor of (1 + z)2. At the same time, the bandwidth dv is reduced by a factor of 1 + z, so the energy flux per unit bandwidth goes down by 1 + z. Also, the observed photons at frequency ν0 were emitted at frequency ν0(1 + z), so the flux density is the luminosity at this frequency, divided by the total area, divided by 1 + z.
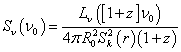
Sν(ν0) = Lv([1 + z]ν0)/4πR02Sk2(r)(1 + z)
The luminosity Lν is measured in units of watts per hertz, W/Hz. Since the emission is not necessarily isotropic, it is common to consider the luminosity emitted into a unit solid angle, in which such case, there would be no factor of 4π, and the units of Lν would be watts per hertz per steradian, WHz-1sr-1.
The specific intensity Iν is the flux density received from a unit solid angle of the sky
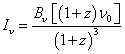
Iν(ν0) = Bν[(1 + z)ν0]/(1 + z)3
Where the surface brightness Bν is the luminosity emitted into unit solid angle per unit area of source. The flux density received by an observer is the product of the specific intensity and the solid angle subtended by the source.
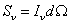
Sν = Iν dΩ
You can integrate over ν0 to obtain the corresponding total or bolometric formulae.

Stot = Ltot/(4πR0Sk2(r)(1 + z)2)
Itot = Btot/(1 + z)4
From this, you can define the angular diameter distance

DA = R0Sk(r)/(1 + z)
and the luminosity distance
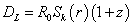
DL = R0Sk(r)(1 + z)
The following is called the effective distance.

R0Sk(r) = (c/H0)(2/(Ω2(1 + z))[Ωz + (Ω - 2)([squareroot of (1 + Ωz)] – 1)