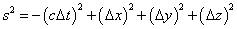
Minkowski metric
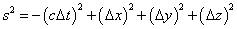
s2 = -(Δt)2 + (Δx)2 + (Δy)2 + (Δz)2
Robertson-Walker metric
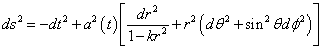
ds2 = -dt2 + a2(t) [dr2/(1 – kr2) + r2 (dθ2 + sin2 θ dφ)]
Schwarzchild metric
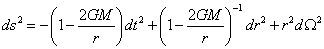
ds2 = -(1 – 2GM/r)dt2 + (1 – 2GM/r)-1dr2 + r2dΩ2
This is the metric of nonrotating uncharged black holes. It was invented by Karl Schwarzschild (1873 - 1916). Notice it reduces to the black holes to the Minkowski metric, when the mass of the black hole is very small, M → 0, or you are very far away from it, r → ∞.
De Sitter metric
Global Coordinates
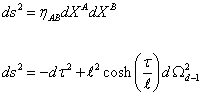
ds2 = ηAB dXA dXB
ds2 = -dτ2 - l2cosh(τ/l)dΩd-l2
Conformal Coordinates
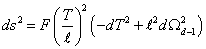
ds2 = F(τ/l)2(-dT2 + l2dΩd – 12)
Planar Coordinates

ds2 = -dt2 + e2t/ldxi2
Static Coordinates
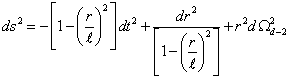
ds2 = -[1 – (r/l)2]dt2 + dr2/[1 – (r/l)2] + r2dΩd – 22
In a strict definition, a universe must have no matter in it, and contain only a positive cosmological constant to be considered a de Sitter universe. However, people usually use a looser definition of de Sitter to mean any maximally symmetric universe with a positive cosmological constant, which would include the real Universe, or at least what the real Universe will evolve into as it becomes increasingly dominated by a positive cosmological constant. A de Sitter universe is often drawn as a hyperboloid in a spacetime diagram.
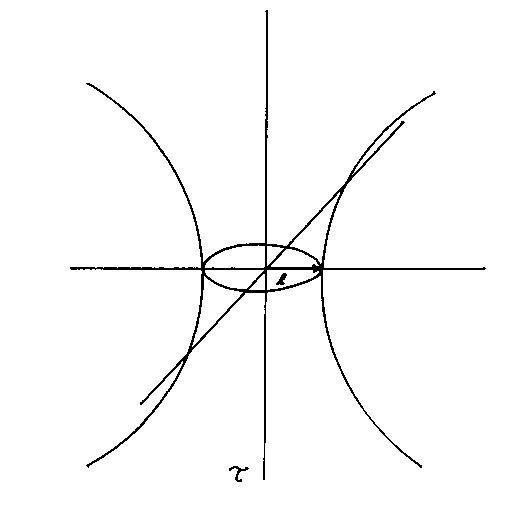
where τ is time, l, which is lower case “L” is the radius, and it contracts from infinity to a finite radius, and expands back to infinity. We are not implying that this diagram represents the behavior of the real Universe, just that’s one way of portraying pure de Sitter space. There are difficulties in making quantum field theory, and thus string theory, consistent with de Sitter space, and since we have evidence for a positive cosmological constant, this is a problem for string theory. Recently, we have come up with an expanded version of M-theory that allowed for de Sitter space, which I discuss at the end of my paper Beyond the Standard Model.
Anti-de Sitter metric
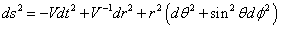
ds2 = -Vdt2 + V-1dr2 + r2(dθ2 + sin2θd&phi2)
where

V = 1 + r2/b2
b = (-3/Λ)½
Anti-de Sitter space is the maximally symmetric space with negative cosmological constant. Although our Universe is obviously not anti-de Sitter, since it has a positive cosmological constant, anti-de Sitter space is important in string theory. In 1997, Juan Maldacena proposed Anti-de Sitter/Conformal Field Theory, or AdS/CFT correspondence, which says that there is a correspondence between Type IIB string theory compactified on AdS5 x S5 and 4-dimensional supersymmetric Yang-Mills theory with N = 4 supersymmetry. I discuss AdS/CFT, correspondence in more detail in my paper Beyond the Standard Model.
Godel Universe

ds2 = -dt2 + dρ2 + sinh2&rhp;(1 – sinh2ρ)dφ2 - 2[squareroot of 2]sinh2ρd + dφ _ dz2
where you have closed time-like curves for constant ρ with

ρ > log (1 + [squareroot of 2]
Originally, the Godel Universe, invented by Austrian mathematician Kurt Gődel (1906 - 1978), was defined as a pressure-free perfect fluid solution in general relativity with negative cosmological constant. It contains closed time-like curves which would allow time travel. Therefore, in order for this model to have anything to do with the real Universe, you would have to get rid of the closed time-like curves. It has been suggested that you could possibly compactify string theory on a Godel Universe, and the holographic principle could possibly get rid of the closed time-like curves. For instance, for supersymmetric backgrounds of the Godel Universe type in string theory and M-theory, a typical example of the metric is
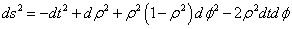
ds2 = -dt2 + dρ2 + ρ2(1 - ρ2)dφ2 - 2ρ2dtdφ
as part of the 10d or 11d spacetime. You have closed time-like curves for ρ > 1.
I have to warn you that there is a whole community of crackpots who have latched onto the Godel Universe as their best hope for time travel, just because they think time travel sounds really neat. Unfortunately for them, time travel is intrinsically impossible, and thus any universe that allows time travel is intrinsically impossible. The problem is that time travel, by definition, involves paradoxes, which go under the heading of the grandfather paradox, which is going back in time, and killing your grandfather when he was a young man. This would mean you never existed, which means you couldn’t prevent your existence, so you would exist, which means you could prevent your existence, etc. You just can’t have time travel without paradoxes, and there’s no way around that. Therefore, the Godel Universe is impossible, since it contains closed time-like curves. Unfortunately, the crackpot community have become champions of the Godel Universe, as if the mere invention of a model universe that allows time travel would somehow allow time travel in the real Universe.
Another model universe that does not correspond to the real Universe is the Milne Universe, also called the kinematical model, invented in the 1930’s by British astrophysicist Edward Arthur Milne (1896 – 1950). It used to be an interesting viable alternative to the standard Big Bang model. Its metric is just the Minkowski metric. In traditional cosmology, there is no outside of the universe. The Milne Universe does have an outside. The universe, filled with ready-made galaxies, is created at a single point in flat spacetime. After that, all the galaxies fill the interior of a bubble that expands at the speed of light into previously empty space. It fills the future light-cone of the Big Bang. The galaxies are treated as non-gravitating test particles. We ignore gravity completely. They all shoot out at different speeds along constant velocity straight line paths inside the bubble. The closer they are to the speed of light, the nearer they will be to the surface of the bubble. You have an infinite number of galaxies filling a bubble of finite size. That might sound impossible, but it is possible if you take into account the length contraction of special relativity. In special relativity, an object that moves relative to some reference frame has a reduced length. Its length contracts to zero as its speed approaches the speed of light. The distance between objects is also contracted. The velocity of the galaxies approach the speed of light as you approach the surface of the bubble so you can fit an infinite number of galaxies within a finite bubble. The person traveling at close to the speed of light will not see their own length contracted. Observers in galaxies close to the surface will not notice anything unusual. All the observers in all the galaxies will see basically the same thing, so the Milne Universe is homogeneous and isotropic. This was a very different way of explaining the expansion of the Universe, although it turned out not to be true.
These various metrics of spacetime can be portrayed graphically by the use of Penrose diagrams, where space is the horizontal axis, and time is the vertical axis. Roger Penrose invented his diagrams in order to depict the complete casual structure of any given geometry. Penrose diagrams map everything in the geometry onto a finite diagram, including points at infinite distance, and infinite past and future. Light rays, called null geodesics, are arranged so that they always point 45° from upward vertical.
You begin with a spacetime with physical metric guv, and introduce an unphysical metric [g bar]uv, which is conformally related to guv by
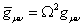
[g bar]μν = Ω2gμν
where the conformal factor Ω is chosen so as to bring in points at infinity to a finite position so that the whole spacetime is shrunk to a finite region called a Penrose diagram. Here is the Penrose diagram of Schwarzchild spacetime.
Here is the Penrose diagram for de Sitter space in static coordinates.
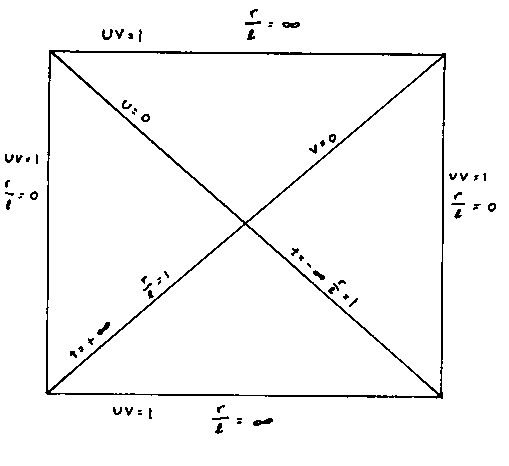
For an observer in any of the four quadrants, the only casual connected region for them in the quadrant that they are in.
From the origin of science in Greece in the 7th Century B.C. up to the 1920’s, it was assumed without question that the Universe had existed forever without beginning. This is despite the fact that Olber’s paradox could be solved by saying the Universe was not infinitely old, but instead the only solution ever suggested was that the Universe was not infinitely large. In 1912, Vesto Slipher measured the redshift of nebulae, which were actually galaxies, and most were redshifted. In 1923 - 1929, Edwin Hubble measured the redshift of the galaxies in detail, which was the first evidence that the Universe had a beginning. There then raged a debate between the Big Bang model and the Steady State model, until the Cosmic Microwave Background was detected in 1964, which was very convincing evidence for the Big Bang model, although a few holdouts continued to cling to the Steady State model. There were some problems with the traditional Big Bang model, such the horizon, flatness, and monopole problems, which were solved by the theory of inflation proposed by Alan Guth and Andrei Linde in 1981. It was later realized that inflation allowed the possibility of eternal inflation, which means the Universe could have existed for an infinite length of time after all, even assuming the Big Bang, so it is still an open question as to whether time extends infinitely backwards or not. Now, the idea that the Universe existed for an infinite length of time poses no problems if you assume that all the stars were printed on the interior surface of the celestial sphere which had existed for an infinite length of time. The celestial sphere was thought to be made out an indestructible crystalline material that could last forever. This cosmological model held the unanimous consensus among physicists and astronomers from the 7th Century B.C. to the 1570’s. Then in 1576, English astronomer Thomas Diggs suggested that there was no celestial sphere, and instead that stars were scattered randomly throughout a huge three dimensional volume of space, perhaps infinitely large. This became the majority view. However, this then posed a problem when combined with Newtonian mechanics, and the assumption that the Universe had existed for an infinite length of time. In Newtonian classical mechanics, all matter attracts all other matter through gravity. Therefore, all the stars would gravitationally attract each other. Given enough time, all the matter in the Universe would collapse together under its own gravity. If the Universe was infinitely old, there would obviously be enough time for this to happen. Instead of interpreting this as evidence against an infinitely old universe, Newton solved the problem by postulating that there existed some sort of repulsive force that counteracted the attraction of gravity. This was the very first suggestion of a cosmological constant. This is the exact same rationale that Einstein used for suggesting a cosmological constant. When Einstein invented general relativity in 1917, it after Slipher first measured the redshift of galaxies but before Hubble’s detailed survey of the redshift of galaxies in the 1920’s, so there was no compelling evidence that the Universe had not existed for an infinite length of time. In physics, you try to think up a theory that explains what you observe. This is exactly what Einstein did when he came up with a model that fit what they observed, which at the time was a stable universe. Therefore, Einstein proposed a cosmological constant that would provide a negative pressure to the universe to counteract the attractive force of gravity.
The problem is that Einstein’s trick of using the cosmological constant to try to make the universe static does not work. Einstein’s model is unstable even with a cosmological constant. Let’s say you have a universe with both matter and vacuum energy. The gravitational attraction of the matter will work to contract the universe. The repulsive effect of the vacuum energy will work to expand the universe. Now, if these two effects cancel each other out exactly, you have a static universe. Now, let’s say you make the universe ever so slightly smaller. Then the matter density will be slightly higher, and thus the gravitational attraction will be slightly higher, but the vacuum density, as always, will be exactly the same, so the repulsive effect will be the same. That means the gravitational attraction and the repulsive effect from the vacuum will no longer cancel each other out, and you’ll have a net gravitational attraction. A net gravitational attraction will cause the universe to contract further, making the matter density even higher, and thus the gravitational attraction even higher. The vacuum energy will be exactly the same so the discrepancy between the magnitude of the gravitational attraction and the repulsive effect of the vacuum energy even greater. This will cause the universe to contract even more. As you see, this sets up a positive feedback loop. Just making the universe just the tiniest possible amount smaller will eventually lead to the entire universe collapsing completely. You also have the same thing in the opposite direction. If you make the universe just slightly larger, the matter density will be slightly lower, and so the gravitational attraction will be slightly lower. The vacuum density will still be exactly the same, so the repulsive effect of the vacuum energy will still be the same. Then the gravitational attraction will not be enough to compensate for the repulsive effect of the vacuum energy, so you will be left with a net repulsion due to the vacuum energy. This will cause the universe to expand even larger, which will cause the matter density to decrease further, which will cause the gravitational attraction to decrease further. Again, you have a feedback loop, and the universe will expand forever. So you see, Einstein’s model of the universe is unstable. The tiniest possible deviation from total perfect cancellation will be exaggerated over time. The tiniest perturbation leads to either contraction or expansion. Therefore, Einstein’s model universe was not stable, and the cosmological constant did not make it stable. Einstein failed to create a static universe but it took several years for people to realize this. In 1930, Eddington showed that Einstein’s model was unstable.
In 1917, before the galactic redshifts were generally known, Einstein proposed a model universe in which random galactic motions cancel out, leaving it static. The mean density of the universe remained constant over time. The radius of the universe remained constant over time. It was a closed universe with spherical geometry. It was finite with no center and no boundary. Einstein then introduced a cosmological constant which was a small repulsive force between matter. This force acts over intergalactic distances and keeps the model from collapsing under its own self-gravitation. In Einstein’s static model, the radius is inversely proportional to the squareroot of the mean density of matter. The mean density is estimated to be between 10-29 and 10-31 g/cm3. This would predict a radius of the universe between 1010 and 10100 light-years. Of course, the observable universe only has a radius of 13.7 billion light-years, since the Universe is 13.7 billion years old. In 1930, Eddington showed that Einstein’s model is actually unstable, and should either expand or contract if perturbed. In 1917, Dutch astronomer William de Sitter (1872 – 1934) proposed another apparently static model, although his model turned out not to be static either. His model contained no matter. It was not really static, and was the forerunner of expanding models. It predicted expansion would last forever. It predicted redshift proportional to distance.
In 1930, Eddington in England proposed a nonstatic model. His model was simply a perturbation of Einstein’s static model. It begins an expansion that lasts forever. Also in 1930, Belgian priest George Lamaitre (1894 – 1966) proposed a nonstatic model. Lamaitre’s model begins with a Big Bang, expands for a while, hesitates in a state resembling Einstein’s static universe, and then expands a second time, and then expands forever. Lamaitre was called the “father of the Big Bang”. In 1922, Russian cosmologist Alaxander Friedman (1888 – 1925) derived nonstatic models that predicted galactic redshifts. His models went unnoticed in the scientific community. According to the Friedman equation, if you assume a mean density equal to the critical mean density, the amount of matter is precisely such that mutual gravitational attraction will stop the expansion when the universe is of an infinite size. This is called a flat or marginally open model. If the mean density is greater than the critical density, the expansion will stop at a finite size, the radius of which is determined by the amount of matter, and is called a closed model. Any value of mean density greater than the critical density, produces one of an infinite family of cosmological models. If the mean density is less than the critical density, even when space becomes infinite, the expansion continues, and is called an open model. Any value of mean density less than the critical density, produces one of an infinite family of cosmological models. In these models, the cosmological constant could be positive, negative, or zero, but non-zero values greatly increase the number of models, and some people believed that the mere proliferation of models argued that the cosmological constant was zero. In 1935, A. G. Walker and H. P. Robertson independently proved that what we now call the Robertson-Walker metric is the only metric consistent with a homogeneous isotropic universe.
In 1912, Vesto Slipher started measuring spectra from nebulae that showed that many appeared to be Doppler shifted, meaning that the frequency of the light was affected by the speed of the source. By 1924, 41 nebula had been measured, and 36 of these were found to be receding. In 1923 – 1929, Erwin Hubble did a more detailed study of galactic redshifts, and determined the proportionality between velocity and distance. Hubble was able to resolve Cepheids in M31, the Andromeda Galaxy, with the 100-inch telescope at Mount Wilson. He developed a new distance measure using the brightest star for more distant galaxies. He correlated these measurements with Slipher’s nebula to discover a proportionality between velocity and distance, and came up with Hubble’s Law, v = Hd. Hubble’s constant H was significantly overestimated by Hubble himself. Here is a plot of Hubble’s 1929 data of radial velocity plotted versus distance.
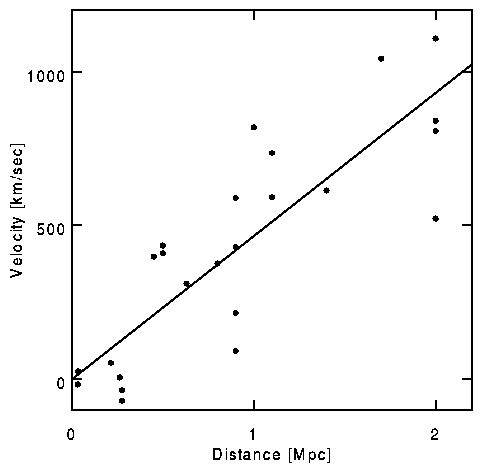
The slope of the tilted line is 464 km/sec/Mpc. Since both kilometers and megaparsecs are units of distance, the units of Hubble’s constant H0 can be reduced to 1/t where
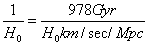
1/H0 = 978 Gyr/(H0 in km/sec/Mpc)
According to Hubble’s data, Hubble’s constant would have a value of two billion years which would be the age of the Universe, except they knew from radioactive dating of rocks that the Earth was older than that. This obviously wrong result gave hope to those who preferred the Steady State model. However, it was later realized that Hubble had confused two different kinds of Cepheid variable stars used for calibrating distance, and also some of what Hubble thought were bright stars were actually HII regions. Hubble’s 1929 data was also unreliable since individual galaxies have individual velocities of several hundred km/sec, in addition to the apparent cosmological recession, and Hubble’s data only went out to 1200 km/sec. This led some people to propose quadratic redshift distance laws. However, later improved data confirmed Hubble’s Law. For instance, the following plot uses data collected by Riess, Press, and Krishner in 1996, using supernovae data.
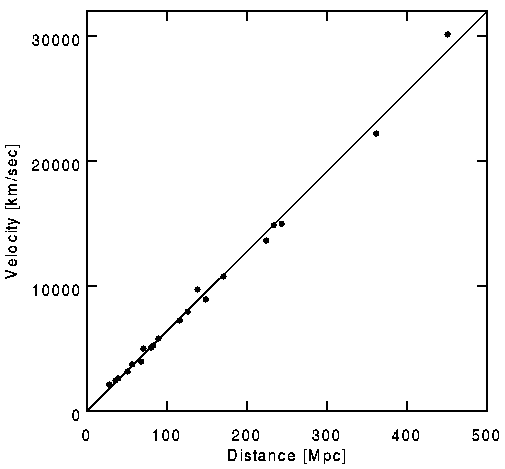
The current estimate of Hubble’s constant based on WMAP data is 0.72 ± 0.05. So as data regarding galactic redshift improved, the evidence for the Big Bang mounted. One thing that’s confusing is that the time and distance used in Hubble’s Law are not the same x and t used in special relativity. Therefore, galaxies far enough away appear to have velocities greater than light. However, they aren’t really traveling faster than light. This is just an artifact of the coordinate system. In 1964, Arno Penzias and Robert Wilson detected the cosmic microwave background. Working with a 7.35 cm microwave horn antenna at Bell Labs, Penzias and Wilson accidentally discovered an isotropic radio background. The cosmic microwave background radiation is key evidence for the hot big bang model. The temperature of this black body radiation is 2.725 K. So you had overwhelming evidence for the Big Bang but there were problems with the traditional Big Bang model. The observable universe is a sphere centered on us, where the radius is the horizon distance, which is the maximum distance light could have traveled since the Big Bang. Thus, the observable universe gets larger as time goes on. Anything within the observable universe is within our past light-cone, and is casually connected to us. Anything outside the observable universe is outside our past light-cone, and is not casually connected to us. If two regions are not casually connected, there is no way they could possibly affect each other. However, when you look to the edge of the observable universe, everything is very similar. The Universe appears homogenous and isotropic, including regions that only recently came within our past light-cone, which means they had to have been very similar before they were casually connected. That sounds impossible. Before they were casually connected, there was no way they could have influenced each other, so what could have made them so similar? This is called the horizon problem.
Another problem is why is the Universe so extremely close to flat? The flatness is indicated by the isotropy of the cosmic microwave background which is isotropic to one part in 105. This is more obvious if you calculate the critical density. The critical density one nanosecond after the Big Bang must have been 447,225,917,218,507,248,016 g/cm3. If you were to add 1 g/cm3 to this, it would cause the Big Crunch to be happening right now. If you were to take 1 g/cm3 away, it would cause Ω to be too low for observations. Therefore, the density one nanosecond after the Big Bang was set to an accuracy of one part in 447 sextillion. At the planck time after the Big Bang, it was set to an accuracy of one part in 1060. What would cause the Universe to be so flat? This is called the flatness problem. Another problem is that phase transitions in the early universe cause topological defects such as magnetic monopoles. The Universe should be filled with monopoles yet we’ve never detected one. This is called the monopole problem. It turns out that the horizon problem, flatness problem, and monopole problem can all be solved by a theory called inflation, which was first suggested by Starobinsky, and later developed by Alan Guth and Andrei Linde in 1981. This assumes that the universe went through a period of enormous accelerated expansion right after the Big Bang, much larger than the accelerated expansion it’s undergoing now. Let’s say you had a sphere with a radius of the planck length before inflation, and inflation only lasted for the planck time. After inflation, the sphere would be several orders of magnitude larger than the current observable universe.
Let’s say you have two tiny regions right next to each other before inflation. This is on the planck scale. They would be similar to each other because they are tiny regions right next to each other, and are casually connected. Inflation would blow them up to huge size, but they would still be similar to each other because they were similar before inflation, and would remain so after inflation. You would then end up with regions that are no longer casually connected but still very similar. Also, inflation would blow up any deviation from flatness much larger than our current horizon length, so what’s within our horizon would appear flat. Inflation would flatten the universe. Also, if regions on the planck scale are blown up to be larger than the observable universe, it’s very unlikely that there would be any monopoles within our observable universe. Therefore, inflation solves the horizon, flatness, and monopole problems. So if the expansion of the universe is caused by the repulsive effect of the cosmological constant, and inflationary cosmology assumes an enormously large amount of expansion in the very beginning of the universe, that means that there was a very large effective cosmological constant in the very beginning of the universe. We have a much smaller but still positive cosmological constant today since the expansion of the Universe is still accelerating, which you can tell from the supernovae Ia data.
Standard cosmology contains a particle horizon of comoving radius
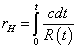
rH = [integral from t to 0] cdt/R(t)
which converges because
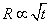
R is proportional to [squareroot of t]
in the early radiation-dominated phase. At late times, the integral is determined by the matter-dominated phase
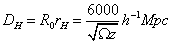
DH = R0rH = 6000/[squareroot of Ωz]h-1Mpc
The horizon at last scattering, z = 1000, was thus only 100 Mpc in size, subtending an angle of about one degree. How is it then possible that the cosmic microwave background is isotropic to one part in 105 all over the entire sky? This is called the horizon problem.
In a flat Ω = 1 universe
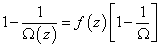
1 – 1/Ω(z) = f(z)[1 – 1/Ω]
where
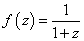
f(z) = 1/(1 + z)
in the matter-dominated era and
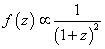
f(z) is proportional to 1/(1 + z)2
in the radiation-dominated era. Therefore
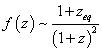
f(z) ~ (1 + zeq)/(1 + z)2
at early times. To get Ω ~ 1 today requires a fine tuning of Ω in the past which becomes more and more precisely constrained as you increase the redshift, and thus go farther and farther backwards in time. Ignoring annihilation effects, you have
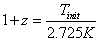
1 + z = Tinit/2.725 K
and 1 + zeq ~ 104, so that the required fine tuning is
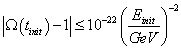
| Ω(tinit) – 1| < 10-22(Einit/GeV)-2
If you choose the planck time as the initial time, this requires a deviation of less than one part in 1060. What could cause the universe to be as flat as that? This is called the flatness problem.
You can solve the horizon and flatness problems if you assume that there was an interval where the universe appeared to be expanding faster than light. Of course, it’s not really traveling faster than light, and this fact is obvious if you look at special relativistic coordinates. If you had such a phase, the integral for the comoving horizon would have diverged, and then the overall homogeneity could be explained by normal casual processes. You could even say that the observed homogeneity proves that such casual contact must have once existed. This is called inflationary cosmology. A period of inflation requires
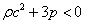
[rho]c2 + 3p < 0
This causes the active mass density
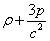
[rho] + 3p/c2
to vanish. Since this is the right hand side of the Poisson equation generalized to relativistic fluids, it’s not surprising that the vanishing ρ + 3p/c2 allows a coasting solution with R proportional to t. Here you have the Friedman equation.
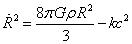
[R dot]2 = (8πGρR2/3) – kc2
With inflation, the density term on the right hand side must exceed the curvature term by a factor of 1060 at the planck time. An inflationary phase in which ρR2 increases as the universe expands can make the curvature term comparatively small.
Inflation requires a state with negative pressure, and the obvious example is p = ρc2 which is the vacuum energy. Therefore, inflation happens in a universe dominated by a cosmological constant. The Friedman equation in the vacuum-dominated case has three solutions.
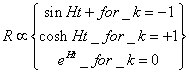
R is proportional to sinh Ht for k = -1
R is proportional to cosh Ht for k = +1
R is proportional to eHt for k = 0
where
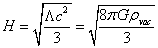
H = [squareroot of (Λc2/3)] = [squareroot of (8πGρvac/3)]
All solutions evolve towards the exponential k = 0 solution, which is de Sitter space. In all models, Ω will tend to unity as the Hubble parameter tends to H0. If the initial conditions are not fine-tuned to Ω = 1, then maintaining the expansion for a factor f gives
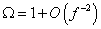
Ω = 1 + O(f-2)
This can solve the flatness problem if f is large enough. To get Ω = 1 today requires
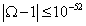
| Ω - 1 | < 10-52
at the GUT epoch, and so
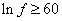
ln f > 60
which means 60 e-foldings of expansion are needed to solve the flatness problem which is the same number as needed to solve the horizon problem. Inflation predicts k = 0.
So our current view of the Universe, inflationary cosmology, assumes a large effective cosmological constant in the beginning of the universe, which causes inflation, which solves the horizon problem, flatness problem, and monopole problem, as well as a small positive cosmological constant today, which causes an acceleration of the expansion of the universe, as indicated by the supernovae Type Ia data. An additional benefit of inflation, and thus the cosmological constant, is that you can use it to explain why the Big Bang happened in the first place. The original traditional Big Bang model gave absolutely no explanation as to why the Big Bang itself happened. The Big Bang itself was just taken as an initial condition without explanation. However, if in the beginning of the universe, there was a period of enormous expansion caused by an effective cosmological constant, you might as well include the Big Bang itself in that, so then the Big Bang itself would be caused by a large effective cosmological constant. So then you have a large cosmological constant in the beginning of the universe which causes the Big Bang and inflation, which solves the horizon problem, flatness problem, and monopole problem, and a small cosmological constant today which explains the acceleration of the expansion of the universe as indicated by the supernovae Type Ia data.
Today, we think of the expansion of the Universe as evidence for the cosmological constant. From our point of view today, we would assume that the detection of the redshift of the galaxies proved the existence of the cosmological constant. However, strangely enough, people at the time said the opposite. When the redshift of the galaxies was first detected, people acted like it proved the nonexistence of the cosmological constant. Einstein said that the cosmological constant was “the biggest blunder of my life”. Why is this? You have to look at it from a historical view. Einstein invented the cosmological constant to keep the universe static. Then when it was learned that the Universe wasn’t static, that means you don’t need a thing the purpose of which is to keep the universe static. If the cosmological constant was invented to keep the universe static, and the Universe isn’t static, that means you don’t need a cosmological constant. Of course, that never proved there wasn’t a cosmological constant. There were nonstatic models with a positive, negative, or zero cosmological constant. However, in physics, you choose the simplest explanation. It was believed that a zero cosmological constant was simpler than a nonzero one. They obviously didn’t need a cosmological constant to explain the horizon, flatness, or monopole problems, or the supernovae Ia data, since none of those things had yet been detected or theorized. As far as the Big Bang itself was concerned, they thought asking what caused the Big Bang was like asking what caused the Universe, which they thought sounded like a metaphysical unanswerable question that was outside the domain of physics to even ask about. At any rate, they reasoned if the Big Bang occurred at t = 0, then there was no “before” so there couldn’t have been anything before that caused it.