
For a particle of mass m, you have one virtual particle in each cubic volume of space, where the length of each side is the Compton wavelength of the particle h/mc, where h is Planck’s constant. The expected energy density is
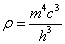
[rho] = m4c3/h3
If you choose m to be the Planck mass, 1019 GeV, that would give 2 x 1091 g/cm3. This is 10120 times larger than the observed value. This is the largest discrepancy between a theoretically predicted value and an experimentally measured value in all of physics. If you take supersymmetry into account, it is only 1055 too large. I explain why in my paper Beyond The Standard Model. Now you can explain this discrepancy if you say that factors we don’t know about cancel each other to give the small net value we detect, which is the premise of renormalization in quantum field theory. In this case, they would have to cancel out to 120 or 55 decimal places. This is possible, but many people feel it is highly unlikely or unnatural. This is called a fine-tuning problem.
You can, of course, just say that the vacuum energy is not the result of particle-antiparticle pairs, and is instead the result of a scalar field rolling down its potential like in the Higgs mechanism. This doesn't have a fine-tuning problem. Today, it is common to say that the cosmological constant is caused by a scalar field rolling down it's potential, and is thus not a constant at all but a varying parameter. This rolling scalar field is called quintessence. It is necessary to have some sort of rolling scalar field to explain both the original inflation and the current acceleration of the expansion of the Universe. With a traditional cosmological constant, w = -1. In the quintessence model, the dark energy is associated with a universal quantum field relaxing towards some final state. Here the energy density and pressure of the dark energy are slowly decreasing with time, and the value of w is somewhere between -1/3 and -1, where w must be smaller than -1/3 in order for cosmic acceleration to occur. It has also been suggested that you could have w < -1, called phantom energy, which could cause the universe to end in a Big Rip, in which all matter is eventually ripped apart by vacuum energy.
Up until the 1980's, most cosmologists took the current cosmological constant to be zero, simply because that would be the simplest model. However, throughout the late 20th Century, there was gradually increasing evidence for a nonzero positive cosmological constant. Mostly, it was indirect. As there were more and more accurate measurements of the amount of matter in the Universe, it became more and more apparent from the isotropy of the CMB, as well as the theory of inflation, that the Universe is very close to flat, and from gravitational lensing, that even including dark matter, the amount of matter in the Universe is not enough to flatten the Universe. Since Ωm + ΩΛ = 1, that means if Ωm < 1, then ΩΛ 0, in other words, we have a positive cosmological constant. Inflation predicted the universe is flat. Then it was realized that the amount of matter in the Universe was not enough to flatten the universe, which meant we had a cosmological constant, would cause the expansion to accelerate. At first we did not detect any such acceleration, but then we did detect it in supernovae data, and many cosmologists breathed a sigh of relief.
The real proof of a positive cosmological constant was when the acceleration of the expansion of the Universe was detected by studying the redshifts of Type Ia supernovae. It’s notoriously difficult to measure interstellar, much less cosmological, distances. For the nearest stars, you can use triangulation, which is basically what George Washington did as a Public Land Surveyor. For distances farther than that, you have to use standard candles. Apparent brightness equals actual brightness divided by the distance squared. Let's say you measure the distance to several nearby celestial objects using parallax or some other means. With the distance and their apparent brightness, you can calculate their actual brightness. If the actual brightness turns out to be the same for all the objects of a given type, you can conclude that the actual brightness is always the same for objects of that type, and it is therefore a standard candle. Now let's say you find celestial objects of that same type too far away for the distance to be measured by any other method. Since you know the actual brightness, and you can measure the apparent brightness, from that you can calculate the distance. Therefore, standard candles are the only way to calculate the distance to distant galaxies. The most famous type of standard candle is Cepheid variables, which are stars for which the brightness is related to the period of the variation in the brightness, so you can calculate the actual brightness. Edwin Hubble used entire galaxies as standard candles but their intrinsic brightness varied widely. As early as 1938, Walter Bade suggested using supernovae as standard candles. For modern cosmology, the main standard candle is Type Ia supernovae. If supernovae have no hydrogen features in their spectra, they are called Type I. If supernovae do have hydrogen features in their spectra, they are called Type II. In the early 1980’s, Type I supernovae were subclassified into Type Ia and Type Ib. If Type I supernovae have a silicon absorption feature at 6150 angstroms in their spectra, they are called Type Ia. If Type I supernovae do not have a silicon absorption feature at 6150 angstroms in their spectra, they are called Type Ib.
A star like the Sun uses up its nuclear fuel in 5 – 10 billion years, and then it shrinks to a white dwarf with its mass, mostly carbon and oxygen, supported against further collapse by electron degeneracy pressure. What if the white dwarf is in a close binary orbit with a large star that is actively burning its nuclear fuel? If conditions are right, there will be a steady stream of material from the active star to the white dwarf. Over millions of years, the white dwarf’s mass builds up until it reaches the critical mass, near the Chandrasekhar limit of about 1.4 solar masses that triggers a runaway thermonuclear explosion called a Type Ia supernova. The slow relentless accretion of material until the characteristic mass is reached erases most of the individual histories and original differences between the stars that collapsed to form the white dwarves. Therefore, the light curves and spectra of all Type Ia supernovae end up being all very similar. Thus, they are excellent standard candles. Since they are bright enough to be seen in the most distant galaxies, they can be used to measure cosmological distances. By measuring both the redshift and the distance of Type Ia supernovae, you can plot redshift versus distance. Two separate teams measured Type Ia supernovae in the late 1990’s. One was the Supernova Cosmology Project led by Saul Perlmutter of Berkeley. The other was the High-Z Supernovae Search led by Brian Schmidt of Australia’s Mount Stromlo Observatory. The results of the two teams confirmed each other.
Type Ia supernovae are very bright and very regular, and can be used as standard candles all the way out to the most distant observable galaxies, and thus can be used to measure the expansion rate of the Universe. However, there were difficulties in using them. First of all, they are rare. A typical galaxy only has a few Type Ia supernovae per millennium. Second of all, they are random, giving no advance warning of where to look. The scarce observing time at the world’s most powerful telescopes is allocated on the basis of proposals written six months in advance. Even the few successful proposals are granted only a few nights a semester. Third of all, they are fleeting. After exploding, they must be observed immediately, and measured multiple times within a few weeks, or they will have already passed the peak brightness that is essential for calibration. You couldn’t preschedule telescope time to identify a supernova’s type or follow it up if you couldn’t guarantee a Type Ia supernova. At the same time, you couldn’t prove a technique for guaranteeing Type Ia supernovae discoveries without prescheduling telescope time to identify them spectroscopically. Eventually, Saul Perlmutter and his team solved this problem. They built a wide-field imager for the Anglo-Australian Observatory’s 4-meter telescope. The imager allowed them to study thousands of distant galaxies in one night, greatly increasing the likelihood of a supernova discovery. By specific timing of the requested telescope schedules, they could guarantee that their wide-field imager would harvest a batch of about a dozen recently exploded supernovae, all discovered on a pre-scheduled observing date during the dark phases of the Moon, which is the best time to do astronomy.
The Supernova Cosmology Project first presented its results in 1997, and it seemed to suggest that the expansion was slowing, but it still had large error bars. In 1998, both the Supernova Cosmology Project led by Saul Perlmutter, and the High-Z Supernova Search, led by Brian Schmidt, presented results that showed that the expansion was accelerating. This proved that we had a non-zero cosmological constant. This should not have been surprising because theoretical cosmologists, such as Michael S. Turner, had long predicted that we had a positive cosmological constant, and should be seeing such an accelerated expansion. By 1990, estimates of the amount of dark matter were getting better but still falling short of enough to flatten the Universe. Observations of large scale structure suggested a cold dark matter or CDM universe with a matter density about one third the critical density, or Ωm = 1/3. Inflationary cosmology predicted a flat universe, or Ω = 1, which is consistent with the isotropy of the cosmic microwave background. Since Ωm + ΩΛ = 1, and Ωm = 1/3, that means ΩΛ = 2/3. That means we have a positive cosmological constant which would cause an acceleration of the expansion. Therefore, the theoretical cosmologists had long been saying that we should observe what the two supernovae teams did observe. The theoretical cosmologists breathed a sigh of relief when the acceleration was finally detected. Despite that, Saul Perlmutter, Brian Schmidt, and their teams were so flabbergasted, they just didn’t believe what they were seeing. They just refused to believe their own data. They assumed it was an experimental error. They went over their own data dozens of times, trying to find the source of the error. If two separate teams had not independently reached the same result, they never would have believed it.
This doesn't make any sense because according to our theories, we should be observing exactly what they observed. It was predicted ahead of time. The supernovae Type Ia data was a confirmation of what our theories predicted we should be observing. Why then were the teams so surprised by this, to the point of disbelieving their own data? If you study physics as I have, you begin to notice that in all fields of physics there is a major communication gap between the theorists and the experimentalists. These are usually very separate communities. This problem seems to be especially pronounced in cosmology. For instance, the cosmic microwave background was predicted in 1949 by Alpher and Herman. Despite that, when it was finally detected in 1964 by Penzias and Wilson, they didn’t know what it was. They assumed it was some sort of problem with their equipment. They even went so far as to try to clean the pigeon shit out of their microwave antennae in order to try to get rid of the annoying background buzz. Similarly, cosmologists like Micheal Turner had predicted in 1990 that we should be observing an acceleration in the expansion due to a positive cosmological constant. This should be easy enough for anyone to understand. If the universe is flat, Ω = 1, and according to observations of large scale structure, Ωm = 1/3, which means ΩΛ must be 2/3. Therefore, the expansion should be accelerating. Despite that, when it was finally detected in 1998 by Saul Perlmutter and Brian Schmidt, they just couldn’t believe it. They assumed it was a systematic error. They went over their data over and over again trying to find the mistake. If two teams hadn't come up with the same result, they never would have believed it. Perhaps this is because decades earlier it had been assumed for simplicity that we had zero cosmological constant, so that’s probably what they were taught in school, and they hadn’t bothered to keep up on the literature. I don't mean to single them out. Most experimental physicists don’t spend much time reading theoretical papers, partly because it's usually over their head. Saul Perlmutter, Brian P. Schmidt, Adam G. Riess received the 2011 Nobel Prize in physics for the discovery of dark energy.
You can point to a similar incident in particle physics in the 1920's. Paul A. M. Dirac came up with Dirac's equation which predicts a negative energy electron, which we now call a positron. Dirac assumed that this was a flaw in his theory, since no such particle was experimentally detected. At the same time, the experimentalists were detecting positrons in cloud chambers all the time, but they just dismissed it as an experimental error, since they thought no such particle was theoretically predicted. It’s only when the experimentalists first heard of this prediction, that Carl Anderson recognized that what they had been seeing all along was Dirac's positron. Carl Anderson was then given credit for "discovering" the positron. I guess the moral of the story is that theorists and experimentalists should be more aware of each other's work.
Also, TIME magazine tried to do a cover story on the Type Ia supernovae data and its implications. Whenever the popular media tries to talk about advanced physics, it’s garbled beyond recognition, and this was a painful example of that. The writer of the TIME magazine article was so utterly clueless, he thought the discovery was that the Universe was not going to end in a Big Crunch. He apparently thought that cosmologists previously thought that the Universe was going to end in a Big Crunch, and they somehow found out that it wasn’t true, when in reality, no one ever thought that anyway.
From the beginning of science in Greece in the 7th Century B.C. until the 1920's, when Edwin Hubble measured the redshifts of galaxies, it was assumed without question that the Universe had existed for an infinite length of time. It never even occurred to anyone to invoke a finite aged universe to explain either Olber’s paradox, or the fact that according to Newtonian mechanics, all the matter in the universe would eventually collapse together due to gravity. In 1912, Vesto Slipher measured the redshifts of spiral nebula and found that many were Doppler shifted. In 1924, 41 nebula were measured, and 36 were found to be receding. In 1923 - 1929, Edwin Hubble measured the proportionality between velocity and distance. Hubble was able to resolve Cepheids in M31, the Andromeda Galaxy, with the 100-inch telescope at Mount Wilson, and developed a new distance measure using the brightest star in distant galaxies. He correlated these measurements with Slipher's nebula, and discovered a proportionality between the velocity and distance called Hubble's Law, v = Hd. Now, if the galaxies are redshifted, that means they are traveling farther apart, and if you extrapolate backwards, they were closer together in the past. As you go farther and farther backwards in time, the galaxies were closer and closer together, the universe was denser and denser, and if you extrapolate all the way back, the universe must have originally been infinitely dense, and that is what we call the Big Bang. Spacetime itself began at a singularity at t = 0, and there was no such thing as before that. Asking what was before t = 0 is like asking what is outside the Universe, what is faster than light, or what is south of Antarctica. It’s a meaningless question with no answer. The discovery of the redshifts of the galaxies was strong evidence for the Big Bang, and that the Universe existed for a finite length of time.
Despite this, about half of cosmologists opposed the Big Bang model, up until the 1960's. Instead, they advocated the Steady State model, which states that the universe had existed for an infinite length of time. Some advocates of the Steady State model tried to explain the redshift of the galaxies with the tired light model which was that light somehow gets redshifted all by itself simply by virtue of traveling a long distance without being stretched by the expansion of space. Steady State theories attempting to explain the redshift without the galaxies getting farther apart, such as the tired light model or the chronometric model proposed by Segal, have since been ruled out by the properties of the CMB. With the tired light model, there is no known interaction that can degrade a photon's energy without also changing its momentum, which leads to a blurring of distant objects which is not observed. Most advocates of the Steady State model conceded that the redshift was due to the galaxies were getting farther apart but claimed that new matter was being constantly created in the space between the galaxies. If that were to happen, the process could continue indefinitely, and the universe could have existed forever. According to the Steady State model, Hubble’s constant really is a constant so that the model has exponential expansion.
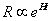
R [proportional to] eHt
same as for de Sitter space. If you look at the transverse part of the Robertson-Walker metric
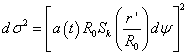
dσ2 = [a(t)R0Sk(r’/R0)dψ]2
The current scale factor R0 then plays the role of the curvature length, determining the distance over which the model is spatially Euclidean. Since the curvature radius would have to be constant in the Steady State model, the only possibility is that it is infinite and k = 0. Therefore, pure de Sitter space, in the original meaning of the phrase, is a Steady State universe. It has constant vacuum energy density, is of infinite age, and has no Big Bang. However, de Sitter space, in the original meaning of the phrase, has no matter.
If you add matter to a Steady State universe, it violates energy conservation since matter does not have the p = -ρc2 equation of state that allows the density to remain constant. Therefore, Steady State models require the continuous creation of matter. Einstein’s equations are modified by adding a creation or C-field term to the energy-momentum tensor.
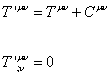
T’uv = Tuv + Cuv
T’;vuv = 0
The effect of this extra term is to cancel the matter density and pressure, leaving just the overall effective form of the vacuum tensor, which is required to produce de Sitter space and the exponential expansion. This field is just added ad hoc, and had no physical motivation except for the problem it was supposed to solve. This Steady State model based on a modified version of general relativity to include a C-field was invented by William McCrea in 1951. In the middle of the 20th Century, the physics community was sharply divided between the Big Bang model and the Steady State model. The Big Bang proponents included George Gamow, Ralph Alpher, and Robert Herman. The Steady State proponents included Herman Bondi, Thomas Gold, and Fred Hoyle. Tempers flared as they argued passionately for their point of view. The Big Bang versus Steady State debate produced some remarkable displays of vitriol. British astronomer and Steady State proponent Fred Hoyle invented the name “Big Bang” as a derisive ridicule of the Big Bang model, and the name stuck.
This situation continued until Arno Penzias and Robert Wilson discovered the cosmic microwave background in 1964. This was interpreted as the faint afterglow of the intense radiation of a hot Big Bang predicted by Ralph Alpher and Robert Herman in 1949. Originally, the Universe was too hot for atomic nuclei and electrons to combine to form electrically neutral atoms. Then 379 ± 8 thousand years after the Big Bang, when the temperature cooled to 3000 K, the nuclei and electrons were moving slow enough to combine to form neutral atoms. Matter became electrically neutral, and matter decoupled from radiation. The photons set free by that decoupling are now being detected by us as cosmic background radiation. You could also think of it as blackbody radiation, like that which inspired Max Planck to come up with Planck’s constant, where in this case, the entire Universe is the cavity. The discovery of the cosmic microwave background provided overwhelming evidence for the Big Bang model. After that, the vast majority of physicists threw their support behind the Big Bang. Yet there remained a few staunch hold out who clung steadfast to the Steady State model. They tried to explain the cosmic microwave background by claiming it originated in interstellar dust. These claims were finally laid to rest in 1990, when it was demonstrated that the radiation was almost exactly Planckian in form. Other evidence for the Big Bang was that, following earlier work by Gamow, Alpher, and Herman in the 1940’s, theorists calculated the relative abundances of the elements hydrogen and helium that were produced in a hot Big Bang, and it was in good agreement with observation. Gamow originally claimed that all the elements were created in the Big Bang. In reality, only hydrogen and helium were created in the Big Bang, and the rest were created in stars.
You have to wonder why did some physicists so strongly prefer the Steady State model to the Big Bang model? Part of it is that they became wedded to a certain theory, and after advocating it so strongly, they became emotionally invested in it, and they were too proud to admit they were wrong, even in the face of overwhelming evidence. However, part of the reason is a justified desire to promote symmetry and invariance under transformations, which is one of the goals of physics. This is why some people today prefer eternal inflation. Physics is filled with symmetry groups, and systems that are invariant under transformations. With special relativity, you have Lorentz invariance. With the Standard Model, you have gauge invariance. You have all the symmetry groups of particle physics, such as SU(3) x SU(2) x U(1), SU(5), SO(10), SUSY, SO(32), E8 x E8, etc. In cosmology, this takes the form of homogeneity and isotropy. Homogeneity is a symmetry of translations, meaning the universe is invariant under translations. Isotropy is a symmetry of rotations, meaning the universe is invariant under rotations. However, if the universe existed for a finite length of time, then it is only homogeneous and isotropic in space but not in time. The universe is homogenous in space, meaning each point in space is basically the same, but it’s not homogenous in time, since each point in time during the history of the universe is not basically the same. The Universe is very different today than it was shortly after the Big Bang. The universe is isotropic in space, meaning if you look in any direction in space, you see basically the same thing, but it’s not isotropic in time, since if you look in any direction in time, you don’t see basically the same thing. If you look to the past, you see a finite length of time, 13.7 billion years, but if you look to the future, you see an infinite length of time ahead of you. Therefore, if the Universe existed for a finite length of time, it is homogeneous and isotropic in space but not in time. If the Universe existed for an infinite length of time, it is homogeneous in both space and time. In physics, you always want everything to be as symmetric as possible. That’s a common theme in physics. According to that, it would be better for the Universe to be homogeneous and isotropic in both space and time. This is called the perfect cosmological principle. This would have been a justified reason for someone to prefer the Steady State model to the Big Bang model, and is why some people today prefer eternal inflation.
Most physicists have no difficulty accepting new theories if they fit the data, and are the best explanation for what we observe. However, some people have a hard time changing their world view. Ernest Mach invented Mach’s Principle, but never accepted the reality of atoms. A whole generation of physicists who grew up on classical mechanics and electromagnetism never fully accepted relativity and quantum mechanics, despite the enormous success of those theories. Paul A. M. Dirac invented the Dirac equation, but never completely gave up the old classical view of particles and fields being two separate things. Similarly, many physicists who their whole lives assumed the Universe existed forever had a hard time accepting the Big Bang model, despite the mounting evidence. To go from the Steady State model to the Big Bang model involves radically changing your world view, and this is difficult for some people. Most physicists are willing to change their theories when confronted with new evidence. However, there are always a few people who just become wedded to a certain theory, and they cling to it even in the face of overwhelming evidence. In the case of the Big Bang, some people especially had difficulty accepting the idea of an initial singularity at t = 0, where there is no such thing as before that. The idea of a beginning of time itself, where there is no such thing as before that, is obviously outside our daily experience, and so it’s hard to imagine what that would be like. That’s not reason to reject it. Relativity and quantum mechanics are also very different from our daily experience, and many physicists initially had a hard time accepting those theories. Sometimes, a major change in our view of the Universe can only be accepted throughout the entire physics community when the older generation is replaced by the younger generation.
Inflationary cosmology was first suggested by Starobinsky, and was developed later by Andrei Linde and Alan Guth in 1981 to explain the horizon, flatness, and monopole problems. Inflation assumes an enormously large amount of expansion at the beginning of the universe. Extremely tiny regions on the planck scale are blown up to be larger than the observable universe. The inhomogeneities of the cosmic microwave background, as well as in the matter distribution, which gave rise to galaxies, originally began as quantum fluctuations. Now, you could imagine that this enormous expansion only took place at the beginning of the universe. Obviously, it’s not going on around us now. However, different parts of the universe could have different values of the scalar inflaton field that drives inflation. Therefore, some other part of the universe that is casually disconnected from us could be undergoing inflation. You could imagine that inflation ended within our observable universe but will always be going on in some parts of the universe, although in other parts it will settle down to a much lower rate of expansion, as in our part. Once you have that, there is no reason why the inflation that created our observable universe had to have taken place right after the Big Bang. It could have taken place any length of time after the Big Bang. You then have to differentiate between the effective local Big Bang, meaning when inflation ended within our part of the universe, which created our observable universe, and the original fundamental Big Bang, which was the origin of the entire universe. The local Big Bang did not necessarily take place right after the original Big Bang. There could have been 10100 years between the original fundamental Big Bang, meaning the real origin of the entire universe, and our local Big Bang, meaning what we observe to be the Big Bang, which created our observable universe.
Once you say that, there is no reason not to take the theory to its logical conclusion, and say that there was no original fundamental Big Bang at all. You could just say that time extends infinitely backwards without beginning. Of course, there was what we normally call the Big Bang, which is the explanation for the redshifts of the galaxies, the cosmic microwave background, the isotropy of the cosmic microwave background to one part in 105, etc. However, with inflation, it is no longer necessary that the Big Bang corresponds to a fundamental beginning of time itself. There could have been a beginning of time, but it’s equally possible that time extends infinitely backwards without beginning. This is almost like resurrecting the Steady State model. Alan Guth, who invented inflation in 1981, holds the view that there was a fundamental beginning of time. Russian cosmologist Andrei Linde advocates the view that time extends infinitely backwards without beginning. Andrei Linde was originally Soviet in addition to Russian, and now he’s American in addition to Russian. His theory that inflation has been going on for an infinite length of time is called eternal inflation. It has the advantage that the entire universe is homogeneous and isotropic in both space and time. Despite that, the vast majority of cosmologists share Alan Guth’s view that there was an original fundamental Big Bang, and Andrei Linde represents a small minority. The reason is similar to what I said earlier about followers of the Steady State model. The current generation of cosmologists grew up on the Big Bang, and the assumption there was a beginning of time. That’s what they were taught in school. Therefore, they feel that is much more logical. They’re not going to change their world view without a reason. Today, there is no observational evidence that can distinguish between normal inflation and eternal inflation, and not much reason to favor one over the other.
I will now explain Alan Guth’s model of inflation in more detail. I assume the reader has read my paper on the Standard Model. You might also want to read the section on grand unified theories in my paper Beyond The Standard Model. In quantum field theory, quantum fields produce an energy density that acts like a cosmological constant. In particle physics, especially extensions of the Standard Model, you have various scalar fields, such as Higgs fields, that could serve as the inflaton driving inflation, where they roll down a potential similar to how they do in the Higgs mechanism. The Lagrangian for a scalar field is kinetic minus potential energy.
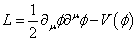
L = ½ [partial derivative]u [phi] [partial derivative]u [phi] – V([phi])
For instance, V(φ) could take the following form
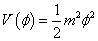
V(φ) = ½ m2φ2
Noether’s theorem gives the energy momentum tensor as
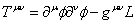
Tuv = [partial derivative]u[phi][partial derivative]v[phi] – guvL
From this, you get the following energy density and pressure
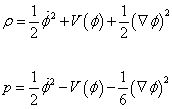
[rho] = ½ [phi dot]2 + V([phi]) + ½ ([nabla][phi])2
p = ½ [phi dot]2 - V([phi]) – 1/6 ([nabla][phi])2
If the field is constant both in space and time, then the equation of state is p = -ρ, which is what you need for it to act as a cosmological constant.
If φ is a complex Higgs field, you then get the symmetry breaking Mexican hat potential of the Higgs mechanism.
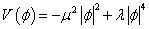
V(φ) = -μ2 |φ|2 + λ|φ|4
At the classical level, this says that |φ| will be located at the potential minimum. This gives the vacuum expectation value
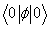
< 0 | φ | 0>
However, this does not include the fluctuations that arise in thermal equilibrium. In classical systems, the non-zero temperature that a system of fixed volume will minimize is not the potential energy but the Helmholtz free energy, F = V – TS, where S is the entropy. The effect of thermal interaction is to add an interaction term to the Lagrangian.
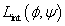
Lint(φ, ψ)
Where ψ is a thermally fluctuating field that corresponds to the heat bath. You would expect Lint to have a quadratic dependence on | φ | around the origin.
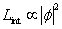
Lint ∝ | φ |2
Otherwise, you would have to explain why the second derivative either vanishes or diverges. The coefficient of proportionality will be the square of an effective mass that depends on the thermal fluctuations in ψ. On dimensional grounds, the coefficient must be proportional to T2.
Therefore, you have to minimize the following temperature dependent effective potential.
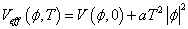
Veff(φ, T) = V(φ, 0) + aT2|φ|2
The effect of this on the symmetry breaking potential depends on the form of the zero temperature V(φ). If the function is of the simple Higgs form
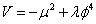
V = -μ2 + λφ4
then the temperature dependent part modifies the effective value of μ2.
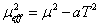
μeff2 = μ2 - aT2
At very high temperatures, the potential will be parabolic, with a minimum at |φ| = 0. Below the critical temperature
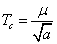
Tc = μ/[squareroot of a]
The ground state is at
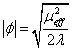
|φ| = [squareroot of (μeff2/2λ)]
and you have broken symmetry. At any given time, there is only a single minimum, so this is a second order phase transition.
You could also have the following more complicated potential.
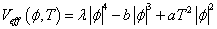
Veff(φ T) = λ|φ|4 - b|φ|3 + aT2|φ|2
which has two critical temperatures. At very high temperatures, the potential will have a parabolic minimum at | φ | = 0. At T1, there is a second minimum in Veff at | φ | ≠ 0. This will be the global minimum for some T2 < T1. For T < T2, the state at | φ | = 0 will be what is called a false vacuum, whereas the global minimum is called the true vacuum.
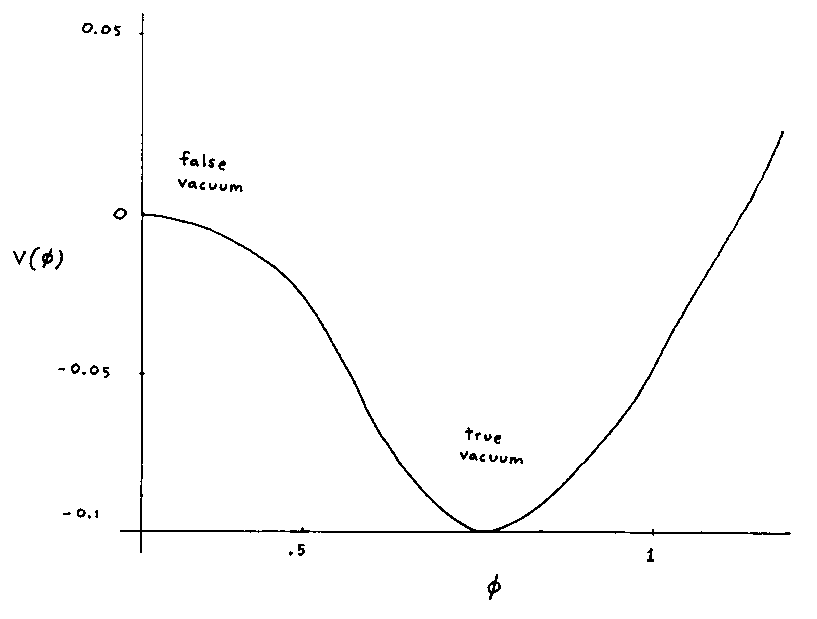
With this potential, the second minimum at φ = 0 always exists, so there is a potential preventing a transition to the false vacuum. This can be overcome by adding a small
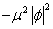
-μ2 |φ|2
component to the potential, so that there will a third critical temperature at which the curvature around the origin chances sign. Also, if the barrier is small enough, there will be quantum tunneling between the false and true vacuum.
The universe is no longer trapped in the false vacuum and can make a first order phase transition to the true vacuum. There will be an energy density difference between the two vacuum states.
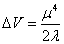
ΔV = μ4/2λ
If you say that the zero of the energy is such that V = 0 in the true vacuum, this means that the false vacuum state acts as an effective cosmological constant. There must be an energy density of m4 in natural units, where m is the energy at which the phase transition occurs. In grand unified theories, m = 1016 GeV, so then
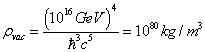
ρvac = (1016 GeV)4/[h bar]3c5 = 1080 kg/m3
Therefore, there is an enormous amount of vacuum energy in grand unified theories, up until GUT symmetry breaking, after which it will stop. Therefore, grand unified theories predict an enormous amount of expansion of the universe at the very beginning of the universe, which is exactly the premise of inflationary cosmology.