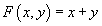
1. The additive formal group law
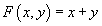
F(x, y) = x + y
2. The multiplicative formal group law
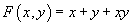
F(x, y) = x + y + xy
This rule can be understood as follows. The product G in the multiplicative group of the ring R is given by G(a, b) = ab. If we change coordinates to make zero the identity by putting a = 1 + x, b = 1 + y, and G = 1 + f, then we find that F(x, y) = x + y + xy. Over the rational numbers, there is an isomorphism from the additive formal group law to the multiplicative formal group law, given by ex - 1. Over a general commutative ring R, there is no such homomorphism since defining it requires non-integer rational numbers, and the additive and multiplicative formal groups laws are usually not isomorphic.
3. More generally, you can construct a formal group law of dimension n from any algebraic group or Lie group of dimension n, by taking coordinates at the identity and writing down the formal power series expansion of the product map. The additive and multiplicative formal group laws obtained in this way form the additive and multiplicative algebraic groups. Another important special case of this is the formal group law of an elliptic curve.
4. The formal group law
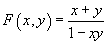
F(x, y) = (x + y)/(1 – xy)
coming from the addition formula for the tangent function

tan(x + y) = F(tan(x), tan(y))
5. The formal group law
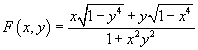
F(x, y) = (x[squareroot of (1 – y4)] + y[squareroot of (1 – x4)])/(1 + x2y2)
is a formal group law over Z[½] found by Euler, in the form of the addition law for an elliptic integral.
Any n-dimensional formal group law gives an n-dimensional Lie algebra over the ring R, defined in terms of the quadratic part F2 of the formal group law
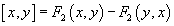
[x, y] = F2(x, y) – F2(y, x)
The natural functor from the Lie groups or algebraic groups to Lie algebras can be factorized into a functor from the Lie groups to formal group laws, followed by taking the Lie algebra of the formal group law.
Lie groups → Formal group laws → Lie algebras
Over fields of characteristic zero, formal group laws are essentially the same as finite dimensional Lie algebras. The functor from finite dimensional formal groups laws to finite dimensional Lie algebras is an equivalence of categories. Over fields of non-zero characteristic, formal group laws are not equivalent to Lie algebras. Sometimes, when you go from an algebraic group to its Lie algebra, you lose too much information, but if you go to the formal group law, you keep enough information. Therefore, you can use formal group laws as a substitute for Lie algebras if the characteristic is not zero.
Let’s say that f is a homomorphism between one-dimensional formal group laws over a field with characteristic p > 0. Then f is either zero or the first non-zero term in its power series expansion is

axph
for some non-negative integer h, called the height of the homomorphism f. The height of the zero homomorphism is defined to be infinity. The height of a one-dimensional formal group law over a field of characteristic p > 0 is defined to be height of its pth power map. Two one-dimensional formal group laws over an algebraically closed field of characteristic p > 0 are isomorphic if and only if they have the same height, which can be any positive integer or infinity.
1. The additive formal group law F(x, y) = x + y has height h = ∞, since its pth power map is 0.
2. The multiplicative formal group law F(x, y) = x + y + xy has height h = 1, since its pth power map is (1 + x)p - 1 = xp.
There is a universal commutative one-dimensional formal group law over a universal commutative ring defined as follows. Let’s say

F(x, y) = x + y + Σ ci, jxixj
For indeterminate ci, j, and we define the universal ring R to be the commutative ring generated by the elements ci, j with the relations that are forced by the associative and commutative laws. For any commutative ring S, one-dimensional formal group laws over S correspond to ring homomorphisms from R to S. The commutative ring R is called Lazard’s universal ring. You might think it would be very complicated, but actually Lazard proved that it has a very simple structure. It is just a polynomial ring over the integers on generators of degrees 2, 4, 6,…, where ci, j has degree 2(i + j – 1). The reason for the strange grading is that Quillen proved that the coefficient ring of complex cobordism is naturally isomorphic as a graded ring to Lazard’s universal ring.
Let’s say Zp is the ring of p-adic integers. The Lubin-Tate formal group law is the unique one-dimensional formal group law F such that e(x) = px + xp is an endomorphism of F.
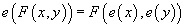
e(F(x, y)) = F(e(x), e(y))
More generally, you can allow e to be any power series such that e(x) = px + higher degree terms, and e(x) = xp mod p. All the group laws for different choices of e satisfying these conditions are strictly isomorphic. For each element a in Zp, there is a unique endomorphism f of the Lubin-Tate formal group law such that f(x) = ax + higher degree terms. This gives an action of the ring Zp on the Lubin-Tate formal group law. There is a similar construction with Zp replaced by any complete discrete valuation ring with finite residue class fields. The Lubin-Tate formal group laws were introduced by Jonathan Lubin and John Tate as part of their successful effort to isolate the local field part of the classical theory of complex multiplication of elliptic functions.
Now I’m going to try to explain elliptic cohomology. I just need to discuss some more preliminary things. An R-valued genus μ is a ring homomorphism
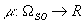
μ : Ωso → R
from the bordisms ring
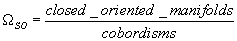
Ωso = (closed oriented manifolds)/(cobordisms)
to R. The product in Ωso is the Cartesian product of manifolds, and the sum is the disjoint union of manifolds. Genera appear as indices of Dirac operators, and are related to the cohomologies of points.
1. The Euler characteristic X → χ(X), which is the index of D = d + d* under the grading by form degree, is close to being a genus, but is not corbordism invariant.
2. The signature genus is the index of D = d + d*, but under the grading of differential forms as positive or negative, according to the signature of the bilinear form
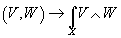
(V, W) → ∫X V ∧ W
3. The [A hat]-genus is the index of a Dirac operator coming from a spinor bundle.
4. The elliptic genus has been interpreted non-rigorously by Witten as the index of a Dirac operator, which is the heterotic string supercharge, on loop space.
Let’s say A is any abelian group. Given a topological space X, there are several equivalent ways to define the nth singular cohomology group

Hn(X, A)
with values in A. One way is to say that this group equals that of homotopy classes of maps from X to the space K(A, n), which is defined to have all homotopy groups trivial except for the nth one, which is isomorphic to A.
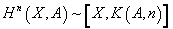
Hn(X, A) ~ [X, K(A, n)]
For this reason, K(A, n) represents ordinary cohomology. It is a simple fact that the based loop space K(A, n) is homotopy equivalent to K(A, n – 1).

ΩK(A, n) ~ K(A, n – 1)
A list
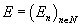
E = (En)n ∈ N
of topological spaces such that each space is the loop space of the next one

ΩEn ~ En – 1
is called a spectrum. The sequence En = K(A, n) is called the Eilenberg-MacLane spectrum, which represents ordinary cohomology. Stated this way, the definition of generalized cohomology is obvious. A generalized cohomology is a collection of functors
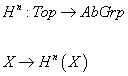
Hn : Top → AbGrp
X → Hn(X)
From topological spaces to abelian groups, which is represented by a spectrum E = (En)
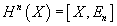
Hn(X) = [X, En]
The first interesting example of a generalized cohomology theory, right after ordinary cohomology, is K-theory.
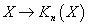
X → Kn(X)
A well-known result by Atiyah says that K0 is represented by the space Fred(H) of Fredholm operators on some separable Hilbert space H.

K(H) ~ [X, Fred(X)]
Some generalized cohomologies have special properties. In particular, we are used to there being a graded ring structure on the cohomology groups, given by the cap product for ordinary cohomology, and by the tensor product of vector bundles for K-theory. It is clear that in order for

H[dot](X) ~ [X, E[dot]]
to be a ring, the spaces E[dot] need to have a ring-like structure themselves. Since everything is defined only up to homotopy, there is freedom in having this ring structure defined only up to higher coherent homotopy. There is one natural choice for how to deal with these higher coherencies.
A spectrum E which is a graded ring
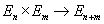
En x Em → En + m
in this higher coherent sense is called an E∞-ring spectrum, or simple an E∞-ring.
An elliptic curve over a field k is the collection of solutions in k x k to an equation in k of the form
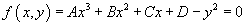
f(x, y) = Ax3 + Bx2 + Cx + D – y2 = 0
where A, B, C, D ∈ k are constants defining an elliptic curve. For the present purpose, the single most important property of an elliptic curve

S = {(x, y) ∈ k x k | f(x, y) = 0}
is that it is naturally equipped with an abelian algebraic group structure S x S → S. Elliptic curves over the complex numbers are precisely the same thing as Riemann surfaces of genus 1, and hence the same as one-loop string diagrams. This makes it quite possible that elliptic curves play a central role in a cohomology theory which assigns to a point in the space of 2dSCFT, the corresponding 1-loop partition function.
We are interested in a 2-dimensional field theory with N = (1, 0) superconformal symmetry, which is the heterotic string. We could also work with Type II superstrings, but these would yield less cohomological information.
There is a graded Hilbert space H of states, which we can think of as something like the space of sections of a spinor bundle over free loop space. Represented on H is the Laplace-like operator
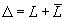
Δ = L + [L bar]
and an operator

P = i(L – [L bar])
which generates rigid rotations of the parametrization of the loops. The chiral combinations

L = ½(Δ + iP)
[L bar] = ½(Δ - iP)
are the zero-modes of the two Virasoro algebras. Let’s say there is an N = (n, m) supersymmetry, essentially up the fact that we’re considering only zero-modes, if there are n mutually graded commuting odd-graded generators G(i) such that
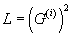
L = (G(i))2
and m mutually graded commuting odd-graded operators [G bar](i) such that
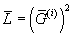
[L bar] = ([G bar](i))2
Restricting to N = (1, 0), you have a single odd-graded operator G with L = G2. We want something like the index of this G. For ordinary supersymmetric quantum mechanics, you compute the index by means of the partition function over a circle of length t, which turns out to be independent of t. Here we compute the partition function over a torus of length t and twist s by
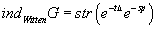
indWittenG = str(e-tΔ e-sP)
indWittenG = str(qL [q bar][L bar])
where

q = e-(t + is)
[q bar] = e-(t – is)
Since L = G2 is the square of an odd operator, the usual argument applies, and we see that this partition function localizes on the kernel of L
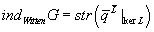
indWittenG = str([q bar][L bar] |ker L)
You can simplify this further by splitting the supertrace into contributions coming from the eigenspaces

Eig(P1 - k) = Hk ⊂ H of P = i(L – [L bar])
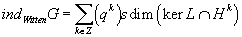
indWittenG = [summation over k &isin Z] (qk) sdim(ker ∩ Hk)
This power series in q is the index of the loop space operator. If you had used N = (1, 1) supersymmetry, the remaining sum would have localized itself on the kernel of [L bar] and collapsed to a mere integer.
indWittenG is a weak integral modular form, which means that
1. It is a holomorphic function f on the upper half plane.
2. It has the transformation property
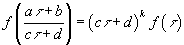
f((aτ + b)/(cτ + d)) = (cτ + d)kf(τ)
for all elements of SL2(Z)
3. Only finitely many terms for negative powers of k are nonvanishing.
4. All coefficients are integers.
All weak integral modular forms are combinations of
1. The discriminant
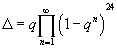
Δ = q[product series over n from 1 to ∞] (1 – qn)24
2. The two Eisenstein series
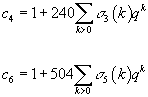
c4 = 1 + 240[summation over k > 0] σ3(k)qk
c6 = 1 – 540[summation over k > 0] σ5(k)qk
where
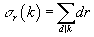
σr(k) = Σd | k dr
The ring of weak integral modular forms, MF* is
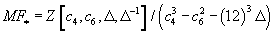
MF* = Z[c4, c6, Δ, Δ-1]/(c43 - c62 - (12)3Δ)
The index of an ordinary Dirac operator takes values in the integers, which is the K-theory of a point. The index of a Dirac operator on loop space takes values in the ring MF* of weak integral modular forms. This lives in something like the elliptic cohomology of a point. The generalized cohomology appearing here comes from an E∞-spectrum called topological modular forms, or tmf.
Let’s say H is some multiplicative generalized cohomology, such as the one coming from an E∞-ring spectrum. You have the graded ring associated by H to the space

K(Z, 2) ~ CP∞ ~ PU(H) ~ BU(1)
Since BU(1) is the classifying space for U(1)-bundles, the ordinary cohomology group H[dot](BU(1), Z) is the ring freely generalized over Z by Chern class c of the universal line bundle U(H) → PU(H). Under the tensor product of two line bundles L1 → X and L2 → X, their Chern classes simply add up in ordinary second cohomology.

c1(L1 ⊗X L2) = c1(L1) + c2(L2)
This particular property turns out to be modified for generalized cohomology theories. They will have other group laws, different from the simple one on the right hand side of the above equation. Let’s say H is any generalized cohomology theory. Its value on BU(1) is always a power series ring

H[dot](BU(1)) = H[dot](pt)[[t]]
over a single generator t of degree 2 with coefficients in the cohomology ring of a point. Remember that t is itself a class of a map
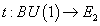
t : BU(1) → E2
if E is the spectrum representing the generalized cohomology.
Given any complex line bundle on some space X, classified by the class of the map φ : X → BU(1), you can pull back the generator t along this map to obtain an element of H[dot](X).

φ*t : X →φ BU(1) →t E2
Notice that for ordinary cohomology, this is precisely the pullback of the universal first Chern class along φ to X, hence the Chern class c1(L) = φ*t of our complex line bundle on X. For generalized cohomologies φ*t is no longer the Chern class of our line bundle. It is instead the generalized Chern class. The whole point of this exercise is that we can now in principle compute how these generalized Chern classes of complex line bundles behave under the tensor product operation of line bundles. They will, in general, unlike the ordinary Chern class, not just add up. For instance, for K-theory, you get the following group law

c1(L1 ⊗X L2) = c1(L1) + c1(L2) + c1(L1)c1(L2)
More generally, you find
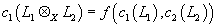
c1(L1 ⊗X L2) = f(c1(L1), c2(L2))
where
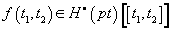
F(t1, t2) ∈ H[dot](pt)[[t1, t2]]
is any formal power series with coefficients in the cohomology ring of a point satisfying the following three axioms.
1. identity – f(x, 0) = f(0, x) = x
2. commutivity – f(x, y) = f(y, x)
3. associativity – f(x, f(y, z)) = f(f(x, y), z)
Such a power series is called a commutative one-dimensional formal group law over the ring H[dot](pt). Under suitable assumptions, over an algebraically closed field, there are only three types of one-dimensional algebraic groups corresponding to three types of formal group laws.
1. The additive group law – x . y = x + y

2. The multiplicative group law – x . y = x + y + xy
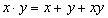
3. A group law defined by an elliptic curve.
An elliptic cohomology is any generalized cohomology whose formal group law, which governs the generalized Chern classes of tensor products of complex line bundles, is given by an elliptic curve. So there are many elliptic cohomology theories. You can do something like taking the direct limit over all of these. The result is represented by an E∞-spectrum called tmf. Its value over a point is the ring of weak integral modular forms that arise as the partition function of heterotic strings.
The Weierstrass form of an elliptic curve E is an equation in two variables x and y of the form
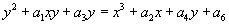
y2 + a1xy + a3y = x3 + a2x + a4y + a6
If the determinant Δ of E is nonvanishing, it is a smooth curve. Thinking of the above equation as living over the real numbers, such smooth curves are certain smooth curves in R2. Straight lines in R2 which coincide with this curve in three points P, Q, and R define an abelian group structure on points by setting

P + Q + R = 0
For many applications, it is convenient to perform a coordinate transformation from (x, y) to (w, z) with

w = -1/y
z = - x/y
Then there is an f such that the above equation for the elliptic curve reads equivalently

w = f(z, w)
By iteratively reinserting f into itself according to this equation, you get
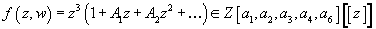
f(z, w) = z3(1 + A1z + A2z2 + …)∈ Z[a1, a2, a3, a4, a6] [[z]]
which is a power series in z starting in degree 3, with coefficients being polynomials in the a’s, over the integers. Using this, you can understand the above addition on the elliptic curve as given by a power series in two variables. Specifically, if (w1, z1) and (w2, z2) are two points on the smooth elliptic curve E, which means that the z coordinate is determined by w, then the result of adding them has a z-coordinate which is given by the power series
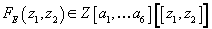
FE(z1, z2) ∈ Z[a1,…a6][[z1, z2]]
This FE is a formal group law, which implies
1. F(z1, 0) = z1
2. F(z1, z2) = F(z2, z1)
3. F(F(z1, z2), z3) = F(z1, F(z2, z3))
for all zj. From this you can show that inverses of all elements exist.
The most famous example of such a formal group law is obtained from taking a one-dimensional real Lie group, looking at the tangent space Te at a given point e, using the exponential map to identify a neighborhood of e in the group with the tangent space, and expanding for all x, y ∈ Te the multiplication in the group as
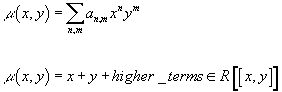
μ(x, y) = Σn, m an, mxnym
μ(x, y) = x + y + higher terms ∈ R[[x, y]]
In general, formal groups are local expansions of group laws. The power series FE associated with a smooth elliptic curve as described above is the expansion of the additive group law defined by the elliptic curve.
Quillen explained that formal groups are related to complex cobordisms. Let MU* be the complex cobordism ring, which is the ring whose elements are cobordism classes of stably complex manifolds with multiplication being the Cartesian product, and addition being a disjoint union.

Ω*U = MU*
This ring is universal for formal group laws in the sense that there is a formal group law

FMU
over MU* such that for every formal group law F over any ring R, there is a unique ring homomorphism
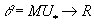
θ : MU* → R
such that
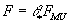
F = θ*FMU
which means that if

FMU(x, y) = Σn, m an, mxnym
then

F(x, y) = Σn, m θ(an, am)xnym
Remember that every elliptic curve E gives rise to a formal group law FE over the ring Z[a1,…a6]. You find that for every elliptic curve, there is a unique ring homomorphism
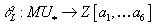
θE : MU* → Z[a1,…a6]
Using this homomorphism, you get an action MU* on Z[a1,…a6]. We want to use this to form a generalized cohomology theory by tensoring Z[a1,…a6] with the universal cohomology MU* theory defined by complex cobordisms.
Let’s set MUn(X) to be the ring of maps

φ : Mn → X
from stably complex n-manifolds Mn to X, where we identify two maps if their domain manifolds are cobounded by a stably complex (n + 1)-manifold, where stably complex means that you can embed Mn in some RN for sufficiently large N, such that the normal bundle Mn in RN is a C-vector bundle. The entire ring MU*(X) is just the direct sum
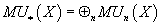
MU*(X) = ⊕n MUn(X)
and in particular, the bare MU* from above is shorthand for the MU-cohomology of a point
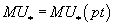
MU* = MU*(pt)
It is important for the following construction that there is a natural graded action MU*(pt) on any MU*(X)
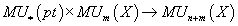
MUn(pt) x MUm(X) → MUn + m(X)
simply given by taking a map
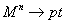
Mn → pt
and
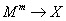
Mm → X
and forming the obvious map
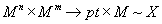
Mn x Mm → pt x M ~ X
Therefore, you have an action of the ring MU*(pt) both on the ring Z[a1,…a6] and on the ring MU*(X) for all X. Therefore, for each elliptic curve E and space X, you can form the graded ring

E*(X) = MU*(X) ⊗MU*(pt) Z[a1,…a6]
This is the elliptic cohomology ring of X with respect to the elliptic curve E. From this, you can recover ordinary integral cohomology and K-theory as degenerate cases of elliptic cohomology. If the elliptic curve is

y2 = x3
with a bad singularity at (0, 0), the corresponding group law is simply
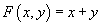
F(x, y) = x + y
This is the group law which corresponds to ordinary integral cohomology.
The elliptic curve

y2 = x3 + x2
has a singularity which is not quite as bad. It gives rise to the group law
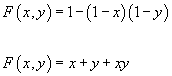
F(x, y) = 1 – (1 – x)(1 – y)
F(x, y) = x + y + xy
This is the group law which corresponds to complex K-theory.
A special case of elliptic curves are the Jacobi curves, which are of the form
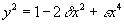
y2 = 1 – 2δx2 + εx4
depending on the two parameters δ and ε. The discriminant is
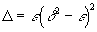
Δ = ε(δ2 - ε)2
Using

g2 = (δ2 - 3ε)/3
g3 = δ(δ2 - 9ε)/27