You can also write

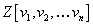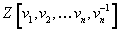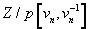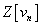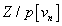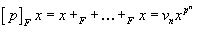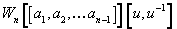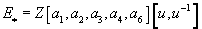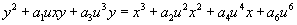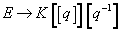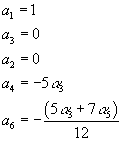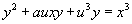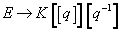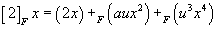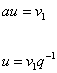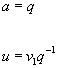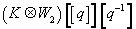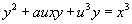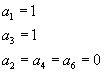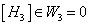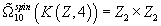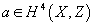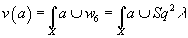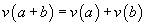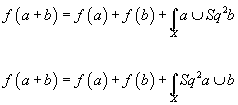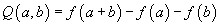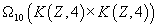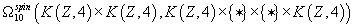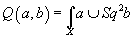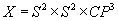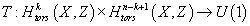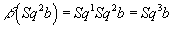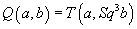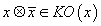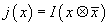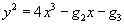
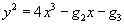
y² = 4x³ - g₂x – g₃

which only works in characteristic > 3. The formal group law corresponding to these curves is

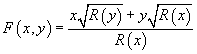
F(x, y) = (x[squareroot of R(y)] + y[squareroot of R(x)])/R(x)

where

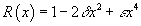
R(x) = 1 – 2δx² + εx⁴

This formula was originally discovered by Euler although he didn't call it a formal group law. You can write F(x, y) as

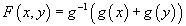
F(x, y) = g^-1(g(x) + g(y))

where

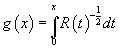
g(x) = ∫₀^x R(t)^-½dt

Now, let [M tilde]_* be the ring of modular forms under the subgroup of SL(2, Z) generated by

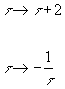
τ → τ + 2

τ = -1/τ

There is a theorem by Landweber, Ravenel, and Stong which says that for δ and ε algebraically independent over Q, you have

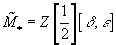
[M tilde]_* = Z[½][δ, ε]

and for all the rings in the diagram

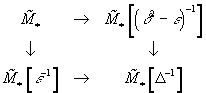
there exist a generalized homology theory h_* such that h_*(pt) is that given ring. This is constructed by noticing that the formal group law defines an action of the oriented cobordism ring on the given ring R_* from above, which allows us to form the homology ring of some space x as

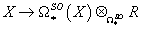
X → Ω_*^SO(X) ⊗_{Ω_*^SO}R

A genus is a ring homomorphism

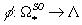
φ : Ω_*^SO → Λ

from oriented cobordisms to any other ring Λ that is also a Q-algebra.

Since

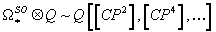
Ω_*^SO ⊗ Q ~ Q[[CP²], [CP⁴],…]

it’s sufficient to specify φ on [CP²ⁿ]. The following expression

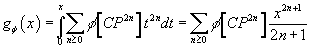
G_φ(x) = ∫₀^x [summation over n ≥ 0] φ [CP²ⁿ] t²ⁿ dt = [summation over n ≥ 0] φ [CP²ⁿ] (x^{2n + 1}/(2n + 1))

is called the logarithm of the genus. Ochanine defined a genus to be elliptic if this logarithm is of the form

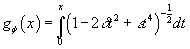
g_φ(x) = ∫₀^x (1 – 2δ t² + ε t⁴)^-½dt

for suitable ring elements δ and ε, algebraically independent over Q and Δ ≠ 0.

There is a theorem by Landweber, Ochanine, and Stong which says that if a genus φ is elliptic, then its image is

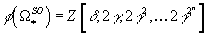
φ(Ω_*^SO) = Z[δ, 2γ, 2γ², …2γ^2ⁿ]

where

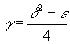
γ = (δ² - ε)/4

Furthermore, the image of its spin cobordism is

φ(Ω_*^spin) = Z[16δ, (8δ)², ε]

Here are some examples.

1. ε = δ = 1

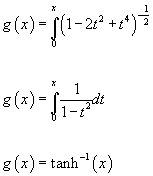
g(x) = ∫₀^x (1 – 2t² + t⁴)^-½dt

g(x) = ∫₀^x 1/(1 – t²) dt

g(x) = tanh^-1(x)

This corresponds to the signature genus or L-genus.

2. ε = 0, δ = -1/8

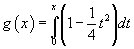
g(x) = ∫₀^x (1 - ¼t²)^-½dt

This corresponds to the [A hat]-genus. As Atiyah and singer found with their famous index theorem, for M compact and dim M = 2n, the [A hat]-genus

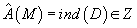
[A hat](M) = ind(D) ∈ Z

is the index of a Dirac operator on M, taking values in the integers.

We want to lift this statement to the loop space of M. It turns out that this is possible if M is string, which means, according to a theorem by Laughlin, that its first two Stieffel-Whitney classes, and one half of the first Pontryagin class, vanishes. In this case, there is something like a Dirac operator on loop space LM, and there is a theorem by Witten and Zagier which says that its index is a genus which is the q-series of a modular form, called the Witten genus, which is the partition function of the heterotic string.

Topological modular forms, or tmf, are like the universal elliptical cohomology. The way elliptic cohomology was defined above depended on the choice of coordinates, in the Weierstrass form, for an elliptic curve. In a vague sense, tmf is the coordinate-free version of elliptic cohomology. The Weierstrass form

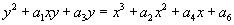
y² + a₁xy + a₃y = x³ + a₂x² + a₄x + a₆

is invariant under the coordinate transformations of the form

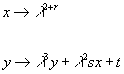
x → λ² + r

y → λ³y + λ²sx + t

where λ is an invertible unit.

Call this group of transformations G. Let

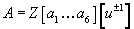
A = Z[a₁,…a₆][u^±1]

and form the cohomology theory

X → (E_A)(X) = MU_*(X) ⊗_{MU_*}A

Then, according to a theorem by Hopkins, Miller, and Goerss, which has been given a more conceptual proof by Jacob Lurie, the G-invariant part (E_A)^G of E_A is a model for tmf. There is a map from the tmf cohomology of a point to modular forms

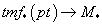
tmf_*(pt) → M

whose kernel and cokernel are annihilated by 24. It is known that

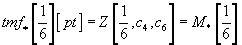
tmf_*[1/6][pt] = Z[1/6, c₄, c₆] = M_*[1/6]

The Witten genus is the composition map

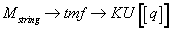
M_string → tmf → KU[[q]]

From string cobordisms over tmf to power series in q with coefficients in K-theory.

The term "elliptic cohomology" was first introduced in 1986 by P. S. Landweber, D. C. Ravenel, and R. E. Stong to designate a cohomology theory obtained by tensoring the oriented cobordism theory with a ring of modular forms in characteristic ≠ 2. Since then, numerous publications have appeared. They attempt to connect elliptic cohomology to other generalized cohomology theories, such as Morava's K-theories. They also attempt to give a geometric interpretation of elliptic cohomology. Despite many very interesting results, there seems to be no consensus on what exactly is the elliptic cohomology. However, the situation is well-understood outside the prime 2. Here, I will describe the Landweber-Ravenel-Stong theory. Let's say Ω_*^SO is the oriented bordism theory with coefficient ring Ω_*^SO, and let

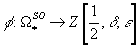
φ : Ω_*^SO → Z[½, δ, ε]

be the level 2 elliptic genus with logarithm

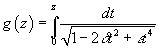
g(z) = ∫₀^z dt/[squareroot of (1 – 2δt² + εt⁴)]

The ring

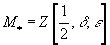
M_* = Z[½, δ, ε]

is a ring of level 2 modular forms in characteristic ≠ 2, and can be viewed, via φ, as an Ω_*^SO-module. It also has a natural grading for which deg δ = 2, and deg ε = 4.

Let π ∈ M_* be any homogenous element of positive degree. Then the functor

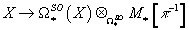
X → Ω_*^SO(X) ⊗_{Ω_*^SO}M_*[π^-1]

is a positive homology theory called elliptic homology, with a coefficient ring M_*[π^-1].

A similar construction using oriented cohomology leads to a multiplicative periodic cohomology theory called elliptic cohomology. The proof of this theorem was first given by Landweber, Ravenel, and Stong under the assumption that π is one of the factors of Δ = ε(δ² - ε)², and was based on Landweber's Exact Functor Theorem, and also interesting congruencies for Legendre polynomials. The general form stated above is due to Jens Franke who showed that the exactness of the functor is a consequence of a theorem by Deuring and Eichler saying that the height of the formal group of an elliptic curve in positive characteristic is always 1 or 2.

A 1-dimensional commutative formal group law (FGL) over a commutative ring R is a series

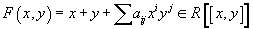
F(x, y) = x + y + Σ a_ijxⁱy^j ∈ R[[x, y]]

which satisfies

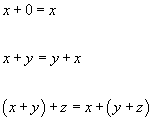
x + 0 = x

x + y = y + x

(x + y) + z = x + (y + z)

The significance in homotopy theory is as follows. We call a ring-valued generalized cohomology theory E complex-oriented if the canonical complex line bundle γ over CP^∞ is E-oriented, meaning it satisfied an E-Thom isomorphism. A choice of such isomorphism is called a complex orientation of E. It follows that every complex bundle is E-oriented. Furthermore, the complex orientation determines a Chern class of complex bundles precisely analogously as in the case of ordinary cohomology. The way FGL's enter the picture is that there exists a unique FGL over the ring E_*, depending only on E and complex orientation, such that for complex line bundles L and M over a space X

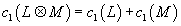
c₁(L ⊗ M) = c₁(L) ⊗ c₁(M)

If you change the complex orientation on E, the formal group law gets replaced by a strongly isomorphic formal group law G which means that there exists a formal series

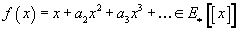
f(x) = x + a₂x² + a₃x³ + …∈ E_*[[x]]

such that

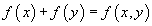
f(x) + f(y) = f(x + y)

The formal group law up to strong isomorphism is a powerful invariant of a complex-oriented generalized cohomology theory. The FGL of ordinary cohomology is additive. F(x, y) = x + y. The FGL of K-theory is multiplicative. F(x, y) = x + y + v₁xy, where v₁ is the Bott element. Over a Q-algebra, all FGL's are isomorphic, just as all rational cohomology theories are equivalent. There is a universal formal group law, which is a commutative ring L with a formal group law F such that for any commutative ring R and any formal group law G on R, there is a unique homomorphism of rings L → R, which carries F to G. This ring was discovered by Lazard. Then Quillen discovered that surprisingly L is isomorphic to the ring of coefficients of MU, complex cobordism which is in some sense the universal complex-oriented generalized cohomology theory.

If we localize at prime p, then MU breaks up as a direct sum of certain theories called BP. There is a corresponding notion of p-typical FGL. The coefficients of BP are

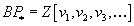
BP_* = Z[v₁, v₂, v₃,…]

dim(v) = 2pⁿ - 2

The formal group law on BP_* was also first observed in algebra, and is due to Cartier. By work of Baas-Sullivan, it is possible to create generalized cohomology theories at will by killing regular sequences in the ring BP_* and/or inverting elements in its coefficient ring. This leads to a menagerie of generalized cohomology theories. Some of the important theories and their coefficients are

1. Johnson-Wilson theory BP(n)

Z[v₁, v₂,…v_n]

2. Landweber theory E(n)

Z[v₁, v₂,…v_n, v_n^-1]

3. Integral Morova K-theory [K tilde](n)

Z[v_n, v_n^-1]

4. Morova K-theory K(n)

Z/p[v_n, v_n^-1]

5. Connective Integral Morova K-theory [k tilde](n)

Z[v_n]

6. Connective Morova K-theory k(n)

Z/p[v_n]

Some of these theories have interesting formal group laws. For instance, the formal group law on K(n)_* has height n which means

[p]_Fx = x + _F +…+_Fx = v_nx^pⁿ

Studying isomorphisms of this FGL led Lubin and Tate to the discovery of the Lubin-Tate FGL on the ring

W_n[[a₁, a₂, …a_{n – 1}]][u, u^-1]

where W_n is the ring of Witt vectors, which are integers of an Eisenstein extension of order pⁿ of the field of p-adic numbers Q_p. The Lubin-Tate coefficient ring turns out to be a completed sum of copies of E(n)_*, and you can consider a generalized cohomology theory with the Lubin-Tate coefficient ring, which is essentially a completed sum of E(n). Lubin-Tate laws were not invented for homotopy theory, but instead for algebraic number theory.

For n = 2, you can also consider cohomology theories whose formal group laws are elliptic, meaning they are obtained by Taylor expansion of the formal group law on an elliptic curve over some commutative ring. Such theories are called complex-oriented elliptic cohomology theories. Ande, Hopkins, and Strickland defined a 2-periodic ring spectrum as a generalized cohomology theory E with an orientation of the identical complex line bundle on CP^∞, which, when restricted to CP¹ has an inverse on E_*. If in addition, E_{2n +
1} = 0 for all n, an evenness condition, and there is an elliptic curve [curly E] over E_* with an isomorphism of its formal group law with the formal group law of E, which is the elliptic spectrum. The word "spectrum" is s term of algebraic topology which means a generalized cohomology theory. The reason for using a separate word is that spectra may be refined to a category which contains a rigid point set level information, analogous to point set level maps of spaces. Cohomology theories see only maps up to homotopy. The rigid level is necessary for certain more complicated constructions such as simplicial realizations.

The elliptic spectrum

E_* = Z[a₁, a₂, a₃, a₄, a₆][u, u^-1]

is associated with the Weierstrass curve

y² + a₁uxy + a₃u³y = x³ + a₂u²x² + a₄u⁴x + a₆u⁶

where dim(x) = 4, dim(y) = 6. The map

E → K[[q]][q^-1]

for this spectrum can be constructed using the Tate parametrization

σ_k(n) = Σ_{d | n} d^k, a_k = Σ_{n > 0} σ_k(n) qⁿ

You can define the above map by

a₁ = 1

a₂ = 0

a₄ = -5α₃

a₆ = -(5α₃ + 7α₅)/12

The coefficients of a₆ turn out to be integers.

At the same time, the Lubin-Tate spectrum

E_* = W₂[[a]][u, u^-1]

is also an elliptic spectrum. Its corresponding elliptic curve is

y² + auxy + u³ = x³

To construct the map

E → K[[q]][q^-1]

in this case, where the target is K-theory with coefficients in W₂, the Lubin-Tate FGL is

[2]_Fx = (2x) + _F(aux²) + _F(u³x⁴)

and Lubin-Tate theory implies that over a ring where au is invertible, this is isomorphic to a multiplicative FGL. Therefore, we define the map by

au = v₁

u = v₁q^-1

or equivalently

a = q

u = v₁q^-1

we get the correct map after composition with the automorphism of

(K ⊗ W₂) [[q]][q^-1]

which sends the formal group law to a multiplicative FGL of K-theory.

y² + auxy + u³y = x³

is a Weierstrass curve with

a₁ = 1

a₃ = 1

a₂ = a₄ = a₆ = 0

However, the map for this theory is not the same as the map coming from the Tate parametrization, thus further confirming the nonuniqueness of the coordinates. Another disadvantage of the theory is that the character map requires you to use

K ⊗ W₂

and thus the Chern character requires crystalline cohomology.

Now, we are finally in a position to use elliptic cohomology to describe superstring theory and M-theory. It might turn out to be more appropriate to use elliptic cohomology than K-theory. There are two superstring theories with two supersymmetries in ten dimensions. One is nonchiral N = (1, 1) Type IIA theory, and the other is chiral N = (2, 0) Type IIB theory. Their fields fall into two sectors, the Ramond-Ramond (RR) sector, and the Neveu-Schwarz (NS) sector. The RR fields naturally couple to D-branes of even spatial dimension in Type IIA. The RR fields naturally couple to D-branes of odd spatial dimension in Type IIB. The NS fields couple to NS-branes. The classification of RR fields has been an active area of research. The charges can be classified, in the absence of NS fields, by K-theory of spacetime. The RR charges are classified by K⁰(X) in Type IIB, and by K¹(X) in Type IIA. The RR fields are classified by K¹(X) for Type IIB, and by K⁰(X) for Type IIA. In the presence of a NS B-field, or its field strength H₃, the relevant K-theory is twisted K-theory. Freed, Witten, and Kapustin showed by analysis of wordsheet anomalies for the case of the NS field

[H₃] ∈ H³(X, Z)

is a torsion class, and by Bouwknegt and Mathai for the non-torsion case. Other versions of K-theory are relevant to string theory. KO and KSp theories are relevant for Type I, equivariant K-theory for orbifolds, and Antiyah’s Real K-theory for orientifolds.

Eleven-dimensional M-theory has four BPS objects, which are the membrane M2, the fivebrane M5, the Kaluza-Klein monopole MKK, and the gravitational wave MW. Compactification on a circle leads to Type IIA. The objects in the theory, such as the M-branes, reduce to Type IIA D-branes. D-branes and M-branes can have anomalies associated with them. This prevents the existence of nonzero or well defined partition functions. For the M5-brane, the partition function is nonzero if the M5-brane can be decoupled from the bulk, including the M2-brane. In Type IIA, the D-brane anomaly cancellation is the vanishing of the third integral Stiefel-Whitney class W₃. In the presence of a NS field, it becomes

[H₃] – W₃ = 0

This can be interpreted in the context of twisted K-theory Atiyah-Hirzebruch spectral sequence (AHSS) as the vanishing of the third differential. This contains a topological part W₃, and twisting part, which is the NS 3-form H₃.

There is another anomaly found by Diaconescu, Moore, and Witten in the context of relating the K-theory of ten-dimensional spacetime X of Type IIA to the partition function of M-theory on an eleven-dimensional manifold Y in the topological sector captured by an E₈ gauge theory. This anomaly is an obstruction to the partition function being well-defined. The condition is the vanishing of the seventh integral Stiefel-Whitney class W₇ of X, considered as the base space of a circle bundle with total space Y. The anomaly still persists in twisted K-theory.

A completely different motivation is to what extent K-theory can describe D-branes, and in particular, the fields and charges, and whether you should seek alternatives in some cases where K-theory breaks down or does not see the whole picture. For instance, on Calabi-Yau spaces, you could use the derived category of sheaves, or the presence of an NS field, the derived category of twisted sheaves. The advantage of using the derived category description of D-branes instead of K-theory is that it contains far more data which specifies the D-brane. On non-geometric backgrounds, such as discrete torsion D-branes, there is a search for a quantum K-theory, such as possibly R/Z generalized cohomology theory. It is natural then to suspect that on general topological spaces, an alternative to K-theory is needed, such as to describe phenomena at strong coupling and at the quantum level, perhaps more “M-theoretic” in nature.

One promising candidate for describing the M-theory partition function is elliptic cohomology. First of all, you might wonder if there is a twisting part that can be added to the topological part W₇ in analogy to H₃ in the brane anomaly. The immediate candidate would be the Hodge dual H₇ = _*10H₃ of H₃. You might wonder whether W₇ analogously comes from a differential of degree 7, d₇ in AHSS. However, K-theory AHSS of a 10-dimensional Spin manifold, d₇ is zero. W₇ can not possibly come from K-theory AHSS. However, it turns out that it does come from d₇, not in K-theory AHSS, but rather in Morova K-theory and elliptic cohomology. The vanishing of the Diaconescu-Moore-Witten obstruction W₇ = 0 is precisely equivalent to orientability of the Spin manifold X with respect to complex oriented elliptic cohomology. This is a generalized cohomology theory which in addition to the Bott periodicity element v₁, contains another periodic element v₂ of dimension 6. Furthermore, v₂ is invertible in elliptic cohomology while v₁ is not. Is there an analog of the M-theory partition function based on elliptic cohomology instead of K-theory? If so, what additional physical information does it contain? Is elliptic cohomology, rather than K-theory, the right tool for describing the path from Type IIA to M-theory?

It now appears that the elliptic cohomology based partition function may be more closely tied to M-theory than the K-theory partition function. For one thing, you can see directly that the elliptic partition function, when it exists, is not anomalous. The distinction between existence and lack of anomaly may seem trivial, but the point is that in the K-theory case, there is a condition of vanishing of a certain quadratic function on torsion. This leads to W₇ = 0. In elliptic cohomology, W₇ = 0 is a condition for orientability, but when satisfied, there is no other condition on torsion. In addition, in elliptic cohomology, you have

E = Z[v₁³, v₂^-1]

so the partition function can be thought of as a family of partition functions indexed by a parameter v₁³v₂^-1. What is the physical meaning of these additional modes? The interpretation of v₂ as an element in the 6-dimensional complex cobordism group suggests that these modes are related to interactions between an M2-brane and an M5-brane. Out of the many possible configurations allowed by supergravity, we think the right ones are intersections between an M2-brane and an M5-brane on a string, which, in the S¹-compactified case, connects with the fundamental Type IIA string. Furthermore, this suggests that the theory can be H₇-twisted, specifically when the M5-brane is not complex-oriented. Even in the untwisted case, we see an anomaly of such states when w₄ ≠ 0.

We also thin that the non-invertibility of the Bott element in elliptic cohomology is related to the disappearance of some of the RR charges when we pass from Type IIA to M-theory. These charges can be constructed from each other in any theory in which the Bott element is invertible.

First, I will briefly review Diaconescu-Moore-Witten M-theory. M-theory is defined on a circle bundle Y with Type IIA on the base space X. In M-theory, there is an E₈ bundle associated to it, with the p₁/2 class λ. In Type IIA, there are RR fields which are reductions of that class, and are classified by twisted K-theory. First, let’s look at the M-theory side compactified to X. Stong has shown that

[Ω tilde]₁₀^Spin(K(Z, 4)) = Z₂ x Z₂

This implies that there are two independent Z₂-valued invariants of the pair (x, a) where

a ∈ H⁴(X, Z)

They are

v(a) = ∫_X a ∪ w₆ = ∫_X a ∪ Sq²λ

where the second integral is due to X being spin. This is a linear function.

v(a + b) = v(a) + v(b)

2. In 8k + 2 dimensions, index D_{v_R} is a topological invariant mod 2,

f(a + b) = f(a) + f(b) + ∫_X a ∪ Sq²b

f(a + b) = f(a) + f(b) + ∫_x Sq²a ∪ b

where f(a) is not a linear function. The form

Q(a, b) = f(a + b) – f(a) – f(b)

is a homomorphism from

Ω₁₀(K(Z, 4) x K(Z, 4))

to Z₂. Q vanishes if either a or b is zero. This implies that Q is a homomorphism to Z₂ of the relative bordism group

Ω₁₀^Spin(K(Z, 4) x K(Z, 4), K(Z, 4) x {*} x {*} x K(Z, 4))

which Diaconescu, Moore, and Witten calculated to be Z₂. One of them is

Q(a, b) = ∫_X a ∪ Sq²b

which is nonzero, such as on

X = S² x S² x CP³

Now let’s say a is a torsion class. Then Q(a, b) is a torsion pairing

T : H_tors^k(X, Z) x H_tors^{n – k + 1}(X, Z) → U(1)

This is because

β(Sq²b) = Sq¹Sq²b = Sq³b

by Adem relations. Now sq³b is a torsion class, and so

Q(a, b) = T(a, Sq³b)

The partition function vanishes unless Q = T = 0. This implies the condition Sq³λ = 0. Therefore, M-theory on a spin manifold of the form X x S¹ is inconsistent if W₇ = 0.

On the Type IIA side, the relevant calculations are K-theory calculations. Remember that we have the mod 2 index I(v) of the Dirac operator with values in a real vector bundle V. For v ∈ KO(X), you can define the mod 2 index I(v) of the Dirac operator with values in v. For any x ∈ K(X), you have

x ⊗ [x bar] ∈ KO(X)

so you can define

j(x) = I(x ⊗ [x bar])