Define the Z₂-valued function

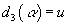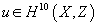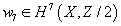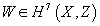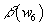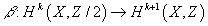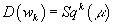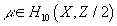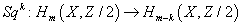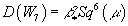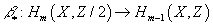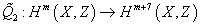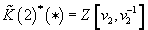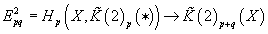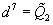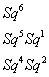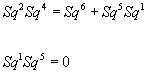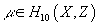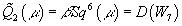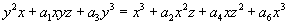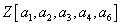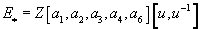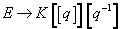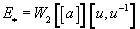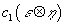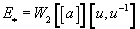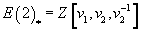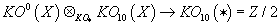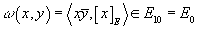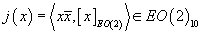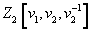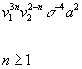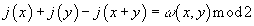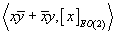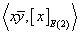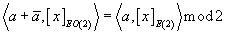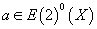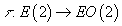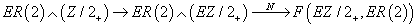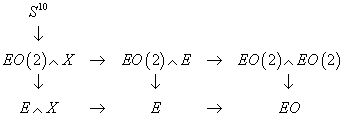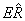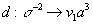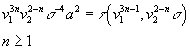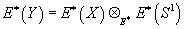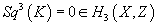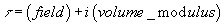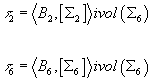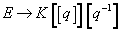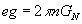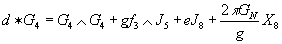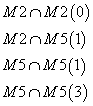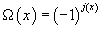
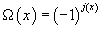
Ω(x) = (-1)^j(x)

which satisfies

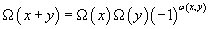
Ω(x + y) = Ω(x)Ω(y)(-1)^{ω(x, y)}

where

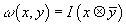
ω(x, y) = I(x ⊗ [y bar])

is an integer-valued unimodular antisymmetric bilinear form on the lattice

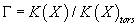
Γ = K(X)/K(X)_tors

Now, if Ω(x) = 1 for torsion elements K(X), then it can be regarded as a function of Γ, and so can be used to define the line bundle, and therefore its section, the RR partition function. If Ω(x) ≠ 1 on K(X)_tors, then the partition function of the theory vanishes upon summing over torsion. It’s similar for twisted K-theory, for

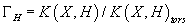
Γ_H = K(X, H)/K(X, H)_tors

Then, in 2003, Diaconsecu, Moore, and Witten showed that the M-theory anomaly and Type IIA are related in a one-to-one fashion.

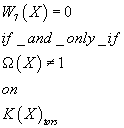
W₇(X) = 0 if and only if Ω(X) ≠ 1 on K(X)_tors

In 1999, Daniel S. Freed and Edward Witten showed that an anomaly in D-branes is given by

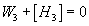
W₃ + [H₃] = 0

where W₃ is the integral class, obtained from the second mod 2 Stiefel-Whitney class, w₂, by the Bockstein homomorphism. A D-brane can’t wrap a submanifold of X unless the Poincare dual can be lifted to K-theory. The anomaly comes from the fact that when this condition is not satisfied then you can have other branes ending on the one you are talking about so you can’t view it in isolation, so the partition function is not well-defined.

At the level of AHSS, it is the third differential d₃ = W₃ + [H₃]. At the level of the full twisted K-theory, you should solve the extension problem, and this could be an obstruction to a K-theory lift. For a compact manifold X, this is an obstruction to being Spin^c. However, there is another way of looking at it, in terms of the K-theory AHSS differential. A Spin^c-manifold would be K-theory orientable, and so would have a K-theory homology fundamental class. Now, you can see directly that if W₃ ≠ 0, then X has no K-theory fundamental class.

Stiefel-Whitney classes are conjugates of Steenrod operations by the Thom isomorphism. However, you can also look at this in terms of Poincare duality. Assuming X is 10-dimensional, let’s say

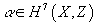
α ∈ H⁷(X, Z)

is a class such that W₃α ≠ 0. Then

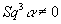
Sq³α ≠ 0

The Milnor primitives Q, invented by J. Milnor in 1958, are elements of the Steenrod algebra of dimension 2^{i + 1} - 1, and

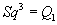
Sq3 = Q₁

where Q is the primary differential d₃ in the K-theory AHSS. So you see that

d₃(α)= u

in the K*-AHSS where

U ∈ H¹⁰(X, Z)

is the dual of the fundamental class. Dualizing, we conclude that the fundamental class X does not lift to K-theory homology, so X is not K-theory orientable.

Next, we’ll discuss W₇. This is not the 7th Stiefel-Whitney class

w₇ ∈ H⁷(X, Z/2)

which always vanishes for a spin manifold. Instead,

W ∈ H⁷(X, Z)

is a canonical integral of w₇, specifically

β(w₆)

where

β H^k(X, Z/2) → H^{k + 1}(X, Z)

is the Bockstein homomorphism. The fact that the mod 2 reduction w₇ of W₇ vanishes signifies the fact that W₇ is divisible by 2 in integral cohomology.

This is analogous to another situation. For a spin manifold X, the first Pontryagin class p₁ is divisible by 2 and λ = p₁/2 is an obstruction to what is called string structure. You might wonder if there is any connection between these two things. One connection is that string structure is the same as thing as lifting the structure group of the tangent bundle on X to a 2-connected cover String(10) of Spin(10).

However, because of Bott periodicity, this is the same thing as the 6-connected cover since there are no homotopy groups between them. In other words, the classifying map X → BSpin(10) lifts to BString(10), which is 7-connected, and there is no cohomology in dimension 7. Therefore, W₇(X) = 0. You have w₆ = Sq²λ so λ = 0 implies w₆ - 0, which implies W₇ = 0. However, it is not true that W₇(X) = 0 implies p₁(X)/2 = 0. For instance, for X = S² x S² x CP³, p₁/2 is nonzero but there is no odd cohomology, so W₇ = 0.

You might wonder what is the geometric meaning of W₇ ≠ 0. Remember the definition of Stiefel-Whitney classes. If you denote the Poincare duality by

D(w_k) = Sq^k(μ)

where

μ ∈ H₁₀(X, Z/2)

is the fundamental class. Remember the actions of the Steenrod operations on homology.

Sq^k : H_m(X, Z/2) → H_{m – k}(X, Z/2)

You therefore have

D(W₇) = β_*Sq⁶(μ)

where

β_* : H_m(X, Z/2) → H_{m – 1}(X, Z)

is the Bockstein.

Now, there is an integral cohomology operation

[Q tilde]₂ : H^m(X, Z) → H^{m + 7}(X, Z)

which is dual to a homological operation lowering the dimension by 7, and which is the integral lift of the Milnor primitive Q₂. Furthermore, the operation [Q tilde]₂ is closely tied to a generalized cohomology theory [K tilde](2) called p = 2 integral second Morova K-theory, which is a reduction of elliptic cohomology. You have

[K tilde](2)*(*) = Z[v₂, v₂^-1]

where v₂ is of dimension 6. The way this theory is tied to [Q tilde] is as follows. For every generalized cohomology, there is a corresponding generalized homology theory. There are Atiyah-Hirzebruch spectral sequences both in homology and cohomology.

Working in homology, the AHSS for [K tilde](2) is

E_pq² =H_p(X, [K tilde](2)_p(*)) → [K tilde](2)_pq(X)

The dimensions imply that possible differentials of this AHSS are d^{6k + 1}. The connection with [Q tilde]₂ is that

D⁷ = [Q tilde]₂

Now, [Q tilde]₂ coincides with βSq⁶ modulo elements of lower Cartan-Serre filtration. There are only three linearly independent Steenrod operations in dimension 6, which are

Sq⁶

Sq⁵Sq¹

Sq⁴Sq²

By Adem relations, you have

Sq²Sq⁴ = Sq⁶ + Sq⁵Sq¹

Sq¹Sq⁵ = 0

On the fundamental scale

μ ∈ H₁₀(X, Z)

The last two must vanish by the assumption that X is a spin manifold.

We conclude that

[Q tilde]₂(μ) = βSq⁶(μ) = D(W₇)

Therefore, you see that W₇ ≠ 0 if and only if the primary differential in the homology [K tilde](2)-AHSS for X is nonzero on μ, which in turn happens if and only if X is not [K tilde](2)-orientable, as any higher differentials are out of filtration degree range. We have therefore proved that a 10-manifold X is orientable with respect to [K tilde](2) if and only if W₇(X) = 0.

It is natural to conjecture that [K tilde](2) can be replaced by elliptic cohomology E. This is in fact true as can be proved by more technical manipulation of the AHSS. Of course, you have to decide which definition of E you want to choose. You can get some insight from looking at the characteristic classes. Notice that W₇ = 0 for any compact complex 10-dimensional manifold, so you should use complex oriented elliptic cohomology. However, the Hopkins-Miller universal elliptic cohomology theory tmf is MO<8>-orientable, which means that every manifold whose stable normal bundle has structure group String = O<8> is tmf-orientable. Therefore, we have an explanation of the above distinction between the p₁/2 and W₇ obstructions. It signifies a connection between M-theory and elliptic cohomology but not tmf.

Now, there are still various models for complex-oriented cohomology E which are characterized by their coefficient rings. Under the assumption that the associated elliptic curve must allow both multiplicative and p = 2-singular reduction, these theories contain equivalent homotopical information but each has advantages and disadvantages. Choosing a complex-oriented elliptic cohomology is like choosing coordinates. The problem is there is no universal complex-oriented elliptic cohomology theory. There is a universal generalized elliptic curve, called the Weierstrass curve

y²x + a₁xyz + a₃y³ = x³ + a₂x²z + a₄xz² + a₆x³

over the ring

Z[a₁, a₂, a₃, a₄, a₆][u, u^-1]

and you can choose

E_* = Z[a₁, a₂, a₃, a₄, a₆][u, u^-1]

This theory is still not universal because of automorphisms. However, the parameters a_i are generalized modular forms, and there is a character map

E → K[[q]][q^-1]

where K is K-theory, q is the parameter of dimension 0, K[[q]] is therefore a product of infinitely many copies of K, and [q^-1] means that q is inverted.

You can simplify is you complete at prime 2. If you choose

E_*= W₂[[a]][u, u^-1]

where W₂ is a ring of Witt vectors, such as the ring of integers, of the extension of the field Q₂ of 2-adic numbers by an Eisenstein polynomial of degree 4, dim(a) = 0, dim(u) = 2. This theory’s formal group law, calculating

c₁(ξ ⊗ η)

from c₁(ξ), c₁(η) for line bundles ξ, η, is a Lubin-Tate law F₂ of height 2. You can construct a character map for this theory, except that k must be replaced by K-theory with coefficients in W₂.

You can simplify it further if you notice that the cohomology theory E with

E_* = W₂[[a]][u, u^-1]

is a completion of a finite sum of suspensions of copies of the cohomology theory E(2) which has

E(2)_* = Z[v₁, v₂, v₂^-1]

where v₁ has dimension 2, and v₂ has dimension 6.

For instance, you can set v₂ = u³, v₁ = au. This cohomology theory lacks some of the manifest modular symmetries of the other elliptic cohomology theories, such as being 6-periodic in dimension, but has the simplest coefficients.

We are dealing with Spin manifolds, so you need a real form EO(2) of elliptic cohomology, which is obtained by taking the fixed point cohomology theory of E under Z/2-action which comes from the FGL isomorphism –i(X), where i(X) is the inverse series of F₂. It’s difficult to make this definition precise since you have to prove the Z/2-action is rigid, and not just up to homotopy. We’ll assume X is orientable under EO(2).

The main point of the construction of the RR partition function of Type IIA D-branes is the function Ω, which is equivalent to j, defined on K⁰(X). From homotopy theory, the construction of j means that for x ∈ K⁰(X), the virtual bundle x ⊗ [x bar] has a real structure, and therefore represents an element of KO⁰(X). The mod 2 index is simply the Kronecker product with the KO-orientation KO-homology class μ ∈ KO₁₀(X)

KO⁰(X) ⊗_KO* KO₁₀(X) → KO₁₀(*) = Z/2

The construction of the partition function fails when this index is nonzero on torsion elements x ∈ K⁰(X).

Now, let’s try to do the same thing with elliptic cohomology. We’ll deal directly with the generalized cohomology class, specifically with E⁰(X)-classes. The manifold X is E-orientable, so it has an orientation class [x]_E ∈ E₁₀X. For x, y ∈ E⁰(X), you have

ω(x, y) = {x[y bar], [x]_E} ∈ E₁₀ = E₀

Now, you need an elliptic refinement of the function j. Assuming that X is EO(2)-orientable, you have an EO(2)-orientation class [x]_EO(2) ∈ EO(2)₁₀(X). Now, for x ∈ E⁰(X), the class x[x bar] lifts canonically to EO(2)⁰(X), so you can put

j(x) = {x[x bar], [x]_EO(2)} ∈ EO(2)₁₀

To see what the right hand side is, you have to compute EO(2)₁₀. It makes the computation easier to reduce E to a theory E(2) with coefficients

Z₂[v₁, v₂, v₂^-1]

It is a direct summand of E so this allows you to leave out repeating terms. You also have the twist. The way you should view the real version of the theory E(2) is as a Z/2-equivariant generalized cohomology theory called ER(2). Cohomology classes of such theories are indexed by k + lα, where α denotes the sign representation of Z/2. The orientation class of X is in ER(2)₁₀(X) so the Kronecker product lies in ER(2)₁₀(*).

This group is a Z/2-vector space with basis

v₁³ⁿv₂^{2 – n}σ^-4a²

n ≥ 1

where v₁ has dimension 1 + α, v₂ has dimension 3(1 + α), σ has dimension α -1, and a has dimension -α, so the generators have dimension 10. Therefore, you have an element

j(x) ∈ Z/2[v₁³, v₂^-1] = EO(2)₁₀

You have to make sense of the identity

j(x) + j(y) – j(x + y) = ω(x, y) mod 2

This is more difficult than the K-theory case since we do not have index-theorectical arguments for E(2), and both sides of the above equation appear to belong to different generalized cohomology groups. However, you can use a purely homotopy-theoretical argument. The left hand side of the above equation is

{x[y bar] + [x bar]y, [x]_EO(2)}

while the right hand side is

{x[y bar], [x]_E(2)}

Therefore, all you have to do is make sense of

{a + [a bar], [x]_EO(2)} = {a, [x]_E(2)} mod 2

for any

a ∈ E(2)⁰(X)

You need the transfer map

τ : E(2) → EO(2)

This can be interpreted as a map on fixed points of the Z/2-equivariant generalized cohomology theories

ER(2) ∧ (Z/2₊) → ER(2) ∧ (EZ/2₊ →^N F(EZ/2₊, ER(2))

where EZ/2 is a contractible space with free Z/2-action. The second arrow N is the norm map from a Borel homology to Borel cohomology theory.

For a ∈ E(2)⁰(X), you have the following commutative diagram.

The unlabeled arrows are forgetful maps and multiplications. This diagram sows that the above equation is valid if we map the right hand side to the left hand side using the transfer. In 2001, P. Hu and Igor Kriz showed that the norm map can be calculated by dividing by σa the differential in the Tate cohomology spectral sequence for

[ER hat]

which crosses the line between Borel homology and cohomology. The relevant differential is

d : σ^-2 → v₁a³

so you get

v₁³ⁿv₂^{2 – n}σ^-4a² = τ(v₁^{3n – 1}, v₂^{2 – n}σ^-5)

n ≥ 1

Now, I’m going to show how elliptic cohomology is related to M-theory. Let’s say you have a 10-dimensional compact Spin manifold X, and put Y = X x S¹. Elliptic cohomology of X and Y are related by the Kunneth theorem

E*(Y) = E*(X) ⊗_E* E*(S¹)

Eⁿ(Y) = Eⁿ(X) ⊕ E^{n – 1}(X)

Let’s say the background is twisted by an NS 3-form H-field. In that case, you must replace K-theory by twisted K-theory. However, C. L. Douglas pointed out that twistings of K-theory determine topological modular forms. Specifically, twistings of K-theory are classified by the space BGL₁(K), and you have a map BGL₁(K) → tmf. Therefore, twistings of K-theory are encoded in tmf, which then maps into E. Therefore, while in twisted K-theory, you must change the theory with each H-field. Elliptic cohomology unifies all of these twisted cases into one theory. This might be because of the connection between elliptic cohomology and 2-vector bundles.

While K-theory twistings give rise to topological modular forms, complex-oriented elliptic cohomology plays a more basic role. This should allow twisting by the field strength H₇, which is the field strength associated with the NS 5-brane, similar to how H₃ is associated with the fundamental string F1. The lift to M-theory of the NS-branes leads to M-branes. The fundamental string expands in one dimension along the M-theory circle to become the M2-brane, while the NS 5-brane lifts to an M5-brane, thus maintaining the same worldvolume dimension. The reason for this difference in codimension in the lifting is because of the dimensions of the relevant forms. In 10 dimensions, the NS field strengths have dimensions three and seven, while in 11 dimensions, the fields have dimensions four and seven. Witten showed that in the case Y = X x S¹, a match between the partition function of M-theory calculated from the G₄-field, which is the field strength associated with the M2-brane, and the Type IIA partition function, which is calculated from the fundamental string RR sector. When increasing the coupling in Type IIA, you get M-theory, compactified on X x S¹, and the fundamental string gets another dimension, and is then identified with the M2-brane. This suggests that the elliptic refinement of the partition function reflects interaction between an M2-brane and M5-brane. The M5-brane is an object in M-theory with electromagnetically dual coupling to the field strength G₄. In Type IIA, it loses a dimension, and becomes a D4-brane. However, using strong-weak duality, you can identify the M5-brane with a 6-dimensional object which is the NS5-brane in Type IIA, which couples magnetically to the NS charge.

Let’s say W is the worldvolume of the NS5-brane. Then the fundamental class κ ∈ H₆(W) must satisfy

Sq³(κ) = 0 ∈ H₃(X, Z)

meaning that κ must lift to the K-theory homology of x. This is also d³ in the E(2)-homology AHSS of X. However, the next differential d⁵ is in homological dimension 1, and therefore is excluded, so κ lifts to a class in E(2)₆(X). Now, by multiplying by the elliptic cohomology element v₂^-1, which is of dimension 6, you get an element of E(2)₀(X). It turns out that 6 is the only dimension of a worldvolume ≤ 10 which can be shifted to 0 by inverting the element v₂. Notice that, unlike in K-theory, the Bott element v₁ is not inverted in elliptic cohomology. This may be singling out the 5-brane as the object whose interactions give the main part of the M-theoretic correction to the Type IIA partition function. In M-theory, the M5-brane couples magnetically to the field strength G₄. In Type II superstring theory, RR D-branes of lower dimension can be generated from higher dimension by tachyonic condensation. This involves the Gysin isomorphism or the Bott element. In M-theory, not all even dimensions are allowed. Specifically, you can not reverse the process, and for instance, turn a 2-brane into a 4-brane in M-theory. This seems to be related to the non-invertibility of the element v₁ in elliptic cohomology.

What might be the twisting with respect to the field strength H₇? Notice that v₂ ∈ MU_* is represented by a complex manifold called a Milnor manifold whose Segre characteristic number is 2. However, an M5-brane, while it must be orientable, may not be a complex manifold. Therefore, it is reasonable to propose the inclusion of such non-complex M5-branes will introduce a new twisting. Elliptic cohomology has the formal group law of an elliptic curve. Therefore, you should be able to see the group, or possibly subgroups of, SL(2, Z). Since the modular parameters that appear in M-theory and string theory are usually of the form

τ = (field) + i(volume modulus)

it seems reasonable to propose the moduli in the form

τ₂ = {B₂, [Σ₂]} + ivol(Σ₆)

τ₆ = {B₂, [Σ₆]} + ivol(Σ₆)

where < , > is the Kronecker product, [ ] is the fundamental class, Σ₂ is a two-cycle that can correspond to F1, and Σ₆ is a six-cycle that can correspond to NS5.

The modular parameter τ₆ should be related to the map

E → K[[q]][q^-1]

by an equation which we can schematically write as

q = e^2πiτ₆

In order to make physical predictions from this, we would need a more precise normalization of coordinates to predict the exact choice of group of modular transformations, as well as a formula for the M5-brane charge.

We still have to interpret v₂^-1v₁³. One possibility is that M2 and M5 coexist, and the membrane modulus is not inverted. If a soliton spectrum contains the M5-brane, then it automatically contains the M2-brane. This can be understood by the Hanany-Witten effect that implies that an M2-brane is created when two M5-branes intersect. Also, an M2-brane appears from the dielectric M5-branes in the limit when the 3-cycle shrinks to zero.

Next, I’ll briefly review the intersections and bound states of M-branes. M2-branes and M5-banes can consistently coexist in compatibility with the gravitational anomaly cancellation. They obey a Dirac quantization condition

eg = 2πnG_N

where e is the M2 charge, g is the M5 charge, and G_N is the 11-dimensional Newton constant. The presence of M2 and M5 modify the equation of motion to

d*G₄ = G₄ ∧ G₄ + gf₃ ∧ J₅ + eJ₈ + (2πG_n/g)X₈

where J₅ is the current Poincare dual to M5, J₈ is the current Poincare dual to M2, X₈ is the 8-polynomial associated with the gravitational anomaly, and f₃ is the M5 worldvolume field. A more detailed analysis would involve Cheeger-Simons differential characters. From supergravity, the allowed supersymmetric intersections are

M2 ∩ M2(0)

M2 ∩ M5(1)

M5 ∩ M5(1)

M5 ∩ M5(3)

where (p) means the intersection is a p-brane. The second one is interesting since it is the intersection over a string of the two types of branes, and is one of the building blocks for brane intersections.

The reduction of the intersection M2 ∩ M5(1) along M2 leads to F1 ending on NS5, and along M5 leads to D2 ending on D4. There are many possible D-brane bound states in Type II string theory. One way they arise is by placing D-branes in a constant background B-field. The worldvolume coordinates of the Dp-brane become noncommutative (NC) along the directions of the nonvanishing B-field. If B is spacelike, you can define a decoupling limit of NCYM, which is NC field theory. If B is timelike, you get noncommutative open string theory (NCOS). In principle, any bound state in Type IIA should have a lift to M-theory. The analogous situation in M-theory would be M-branes in a constant background C-field. The configuration of M2-branes ending on M5 is the lift of strings ending on D-branes. You can also have a decoupled theory, the light Open Membrane (OM). Six-dimensional OM-theory is the high energy limit of 5-dimensional NCYM and NCOS. Compactification of OM-theory on an electric circle leads to NCOS. Compactification of OM-theory on a magnetic circle leads to NCYM. A constant background C-field is equivalent to a constant M5 worldvolume field f₃. This represents a bound state of this M5 with a delocalized M2 along 2 of the 5 spatial dimensions of M5. Many of the bound states involving different combinations can be related to (M2, M5) by a Lorentz transformation, and this seems to indicate that the latter is the basic bound state.

This suggests that you can use the IIA-side to interpret the elliptic refinement, since the G₄ approach should be exactly dual. The IIA side is easier to work with since you have the usual expansion of the radial excitation modes of the fundamental string. The meaning of the parameter v₂^-1v₁³ is that it comes from the interaction with a complex oriented M5-brane, and that the partition function should be twisted if the M5-brane if the M5-brane is not complex-oriented. Therefore, we should consider what kinds of possible bound states between M2-branes and M5-branes that you can have. one possibility is that an open M2-brane is a boundary of an M5-brane. This is suggested by the non-invertibility of v₁, and therefore v₂^-1v₁³ in elliptic cohomology. However, from the point of view of the M5-brane, it is not clear whether such states would be anomalous. Also, in the IIA-dimensional reduction, there is no direct role of the open string partition function. it may therefore be that rather than ending on the M5-brane, the M2-brane intersects the M5-brane in a fundamental string, and the elliptic partition function reflects the energy that the bound state gets from the intersection. You could also claim that just as in string theory, where open strings require closed strings, that here open membranes seem to be only needed to imply the existence of the branes, and they do not enter into the calculation of the partition function.

The elliptic refinements of the IIA partition function, or alternatively the M-theory G₄ partition function, picks up states arising from the intersection of an M2-brane with an M5-brane, which could be H₇-twisted if the M5-brane is not complex-oriented. In the present untwisted case, there is an anomaly of these states when w₄ ≠ 0. On the IIA side for Y = X x S¹, the intersection is the end of the Type IIA fundamental string. The elliptic function after suitable renormalization and computation of the 5-brane charge should compute the M2-M5 intersecting state correction to the G₄ M-theory partition function. Orientability with respect to EO(2) is equivalent to vanishing w₄. This is relevant to M-theory backgrounds as well as to the M5 anomaly. In 2000, Witten showed that G₄/2π is quantized as w₄/2 mod Z. The condition w₄ - 0 implies that there are no half-integral fluxes, which is the case for the relevant Z₂-orbifolds and orientifolds. Witten also showed that w₄ also shows up as part of the mod 2 index and therefore, the anomaly for the M5-brane.