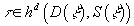
Now I'll discuss the Thom isomorphism theorem. Let ξ → X be a d-dimensional vector bundle over a topological space X, and let h+ be a multiplicative generalized cohomology theory. Let
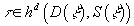
τ ∈ hd(D(ξ), S(ξ))
be a Thom class for ξ where D(ξ) is the disk bundle of ξ, and S(ξ) is the sphere bundle of ξ. Since h+ is a multiplicative theory, there is a generalized cup product map
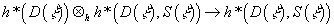
h*(D(ξ)) [direct product]h*h*(D(ξ), S(ξ)) → h*(D(ξ), S(ξ))
where the tensor product is over the coefficient ring h*(pt) of the theory. Using the isomorphism
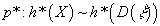
p* : h+(X) ~h*(D(ξ))
induced by the homotopy equivalence p : D(ξ) → X we get the homeomorphism
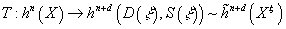
T: hn(X) → hn x d(D(ξ), S(ξ)) ~ [h tilde]n + d(Xξ)
Taking α to p*(α) . τ. And where Xξ is the Thom space D(ξ)/S(ξ) of ξ. The Thom isomorphism theorem then says T is an isomorphism
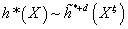
h*(X) ~[h tilde]*+ d(Xξ)
of graded modules over h*(pt).
There's one last subject I have to discuss before we begin. A character class is a way of associating to each principle bundle on a topological space X, a cohomology class of X. The cohomology class measures the extent to which the bundle is twisted, especially whether it contains sections or not. Therefore, characteristic classes are global invariants which measure the deviation of a local product structure from a global product structure.
If G is a topological group for a topological space X, then bG(X) is the set of isomorphism classes of principle G-bundles. bG(X) is a contravariant functor from the category of topological spaces and continuous functions to the category of sets and functions, or Top → Set, sending a map f to the pull back operation f*. A characteristic class c of principle G-bundles is then a natural transformation from bG(X) to a cohomology functor H*, which is also a functor to Set. Therefore, the characteristic class c is a transformation from one functor to another. A characteristic class associates to any principle G-bundle P → X an element c(P) in H*(X) such that if f : Y → X is a continuous map, then c(f*P) = f*c(P). On the left is the class of the pull back of P to Y. On the right is the image of the class of P under the induced map in cohomology.
Characteristic classes are contravariant constructions, thus belonging to cohomology theory in that a section is a kind of function on space. Cohomology was developed after homology and homotopy which are covariant theories mapping into space. Characteristic classes were first considered in the 1930s, and they were a major reason why a dual theory to homology was sought. The characteristic class approach to curvature invariants was one of the primary motivations to developing cohomology, in order to prove the Gauss-Bonnet theorem. When the theory was organized around 1950, it became clear that the most fundamental characteristic classes known at the time, which were the Chern class, the Pontryagin class, and the Stiefel-Whitney class, were reflections of the classical linear groups and their maximal torus structure. It was realized that the Chern class had been foreshadowed by the Schubert calculus on Grassmannians, and the Italian school of algebraic geometry. However, now there was a framework which produced families of classes whenever there was a vector bundle involved.
Given a space X carrying a vector bundle, that implied in the homotopy category, a mapping from X to a classifying space BG, for the relevant linear group in G. For homotopy theory, the relevant information is carried by the compact subgroups, such as the orthogonal groups and the unitary groups of G. Once the cohomology H*(BG) was calculated, the contravariant property of cohomology meant that the characteristic classes for the bundle would be defined in H*(X) in the same dimensions. For example, the Chern class is really one class with graded components in each even dimension. With the advent of extraordinary cohomology theory, when K-theory and cobordism theory were developed in 1955, it was really only necessary to change the letter H everywhere to say what the characteristic classes were.
Chern classes, pronounced "Chen", were invented by Shiing-Shen Chen in 1940. A chern class is a gadget defined for complex vector bundles. The Chern classes of a complex manifold are the Chern classes of its tangent bundle. The ith Chern class is an obstruction to the existence of an (n - i + 1) everywhere complex linearly independent vector fields on that vector bundle. The ith Chern class is in the (2i)-th cohomology group of the base space.
Chern classes are topological invariants associated to vector bundles on a smooth manifold. If you describe the same vector bundle on a manifold in two different ways, the Chern classes will be the same. How can you tell if two vector bundles are the same? If the Chern classes of two vector bundles are different then the vector bundles must be different, although if they are the same, it doesn't mean that the vector bundles are the same. It is often important to count how many linearly independent sections a vector bundle has. The Chern classes offer some information about this, such as through the Riemann-Roch theorem and the Atiyah-Singer index theorem. Chern classes are also easy to calculate since they can be expressed as polynomials of coefficients of the curvature form.
Given a complex hermitian vector bundle V of complex rank n over a smooth manifold M, a representative of each Chern class, also called a Cern form, ck(V) of V, are given as the coefficients of the characteristic polynomial of the curvature form Ω of V.
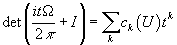
det((itΩ/2π) + I) = [summation over k] ck(V)tk
where Ω is the curvature form, the scalar t is an indeterminate to generate the sum from the determinate, and I is the n x n identity matrix.
The determinant is over the ring of n x n matrices whose entries are polynomials in t with coefficients in the commutative algebra of even differential forms on M. The curvature form Ω of V is defined as
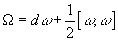
Ω = dω + ½ [ω, ω]
where ω is the connection, and d is the exterior derivative, or via the same expression in which ω is a gauge form for the gauge group V.
When you say "Chern class", you mean "class up to addition of a differential form". Therefore, Chern classes are cohomology classes in the sense of de Rham cohomology. It can be shown that the cohomology class of the Chern forms do not depend on the choice of connection in V.
If you ever look at a little girl in pigtails, you see they have a vertical line down the back of their head. If you try combing the hair of a child, you see there are lines where on one side, the hairs point in one direction, and on the other side, the hairs point in the other direction. Let's say you have a vector field on a sphere.

Is it possible to arrange the vectors in such a way so there is no point on the sphere where they suddenly change direction? The answer to the question is "no". This is called the hairy ball theorem, which states you can't comb a hairy ball flat. This fact can be proved using Chern classes.
Let's say you have one-dimensional complex projective space, CP1, also called a Riemann sphere. Let's say z is a holomorphic local coordinate for the Riemann sphere. Let V = TCP1 be the bundle of complex tangent vectors having the form a ∂/∂z at each point, where a is a complex number. You can prove that V has no section that is everywhere nonzero, proving the complex version of the hairy ball theorem.
The first Chern class of a trivial bundle is zero.
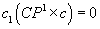
c1(CP1 x C) = 0
We need to show that
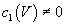
c1(V) ≠ 0
If you have the Kahler metric
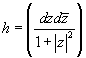
h = (dz d[z bar]/(1 + | z |2)
The curvature z-form is given by
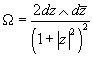
Ω = (2dz ∧ d[z bar])/(1 + | z |2)2
The definition of the first Chern class is
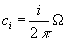
c1 = (i/2π)Ω
You compute its integral over the Riemann sphere.
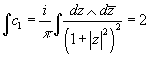
[integral]c1 = (i/π) [integral] (dz ∧ d[z bar])/(1 + | z |2)2
after switching to polar coordinates. By Stokes theorem, an exact form would integrate to 0, so the cohomology class is non-zero. This proves that TCP1 is not a trivial vector bundle, proving the complex version of the hairy ball theorem.
Given a complex vector bundle V over a topological space X, the Chern classes of V are a sequence of elements of the cohomology of X. The kth Chern class of V, written ck(V) is an element of
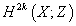
H2k(X ; Z)
The cohomology of X with integer coefficients. You can also define the total Chern class as
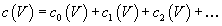
c(V) = c0(V) + c1(V) + c2(V) + ...
The Chern classes obey the following four axioms.
1. c0(V) = 1 for all V
2. Functorality : If f : Y → X is continuous, and f*V is the vector bundle pull back of V, then ck(f*V) = f*ck(V).
3. Whitney sum formula: If W → X is another complex vector bundle, then the Chern classes of the direct sum V + W are given by
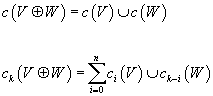
c(V + W) = c(V) ∪ c(W)
ck(V + W) = [summation of i from 0 to n]ci(V) ∪ ck - i(W)
4. Normalization : The total Chern class of the tautological line bundle over CPk is 1 - H, where H is the Poincare dual to the hyperplane CPk - 1 ⊂ CPk.
Alexander Grothendieck managed to replace these with the following three axioms.
1. Functorality : If f : Y → X is continuous, and f*V is the vector bundle pull back of V, then ck(f*V) = f*ck(V).
2. Additivity : If 0 → E → E' → E" → 0 is an exact sequence of vector bundles, then c(E) = c(E') = c(E").
3. Normalization : If E is a line bundle, then c(E) = 1 + e(ER, where e(ER) is the Euler class of the underlying real vector bundle.
These properties uniquely uniquely characterize the Chern classes. They imply
1. If n is the complex rank of V, then ck(V) = 0 for all k > n. This the total Chern class terminates.
2. The top Chern class of V, meaning cn(V) where n is the rank of V, is always equal to the Euler class of the underlying real vector bundle.
A Calabi-Yau manifold is a Kahler manifold with vanishing first Chern class. A Calabi-Yau manifold of complex dimension n is called a Calabi-Yau n-fold. In 1957, Eugenie Calabi conjectured that all such manifolds admit a Ricci-flat metric, one in each Kahler class, and this was proved by Sing-Tung Yau in 1977. A Calabi-Yau n-fold is a manifold with SU(n) holonomy. The first Chern class vanishes if and only if the canonical bundle is trivial, which is the case if and only if the canonical bundle is the zero class. Here is a 3D slice of a 6D Calabi-Yau manifold used in superstring theory.

Aside from the Chern class, another characteristic class is the Pontryagin class. The ith Pontryagin class of a vector bundle is (-1)i times the ith Chern class of the complexification of the vector bundle. It is also the 4ith cohomology group of the base space involved.
Given a vector bundle E over M, its k-th Pontryagin class pk(E) is defined as
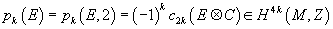
pk(E) = pk(E, Z) = (-1)kc2k(E [direct product] C) ∈ H4k(M, Z)
where
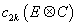
c2k(E [direct product] C)
is times the 2k-th Chern class of the complexification
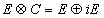
E x C = E + iE
Of E and H4k(M, Z), the 4k-th cohomology group of M with rational coefficients.
Pontryagin classes have a meaning in real differential geometry, as opposed to the Chern class which assumes a complex vector bundle.
If all Pontryagin classes and Stiefel-Whitney classes of E vanish, then the bundle is trivial. Its Whitney sum with a trivial bundle is trivial. The total Pontryagin class
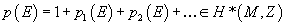
p(E) = 1 + p1(E) + p2(E) + ... ∈ H*(M, Z)
is multiplicative with respect to the Whitney sum of vector bundles.
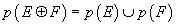
p(E + F) = p(E) ∪ p(E)
for two vector bundles E and F over M
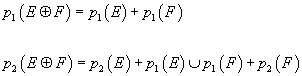
p1(E + F) = p1 + p1(F)
p2(E + F) = p2(E) + p1(E) ∪ p1(F) + p2(F)
Given a 2k-dimensional vector bundle E you have
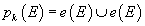
pk(E) = e(E) ∪ e(E)
where e(E) is the Euler class of E, and ∪ is the cup product of cohomology classes.
In 1948, Shiing-Shen Chern and Andre Weil proved that the rational Pontryagin classes
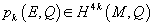
pk(E, Q) ∈ H4k(M, Q)
can be presented as differential forms which depend polynomially on the curvature form of a vector bundle. This Chern-Weil theory revealed a major connection between algebraic topology and global differential geometry.
For a vector bundle E over an n-dimensional differentiable manifold M equipped with a connection, its k-th Pontryagin class can be realized by the 4k-form
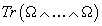
Tr(Ω ∧ ...∧ Ω)
constructed with 2k copies of the curvature form Ω. The value
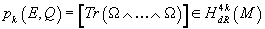
pk(E, Q) = [Tr(Ω ∧ ...∧ Ω)] ∈ HdR4k(M)
does not depend on the choice of connection. H*dR(M) is the de Rham cohomology groups.
The third main type of character class, after the Chern class and Pontryagin class, is the Stiefel-Whitney class. The ith Stiefel-Whitney class of a real vector bundle, or tangent bundle on a real manifold, is in the ith cohomology group of the base space involved. It is an obstruction to the existence of (n - i + 1) real linearly independent vector fields on that vector bundle, where n is the dimension of the fiber. Here "obstruction" means that the ith Stiefel-Whitney class being nonzero implies that there do not exist (n - i + 1) everywhere linearly dependent vector fields, although the Stiefel-Whitney classes are not always the obstruction. In particular, the nth Stiefel-Whitney class is the obstruction to the existence of an everywhere nonzero vector field, and the first Stiefel-Whitney class of a manifold is the obstruction to orientability.
Stiefel-Whitney classes are a type of characteristic class associated to real vector bundles E → X. They are written wi(E) taking values in Hi(X, Z2), the cohomology groups with mod 2 coefficients. For example, over the circle, S1, there is a line bundle that is topologically non-trivial, that is the line bundle associated with the Möbius strip, usually thought of as having fibers [0, 1]. The cohomology group
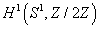
H1(S1, Z/2Z)
has just one element other than 0, which is the first Stiefel-Whitney class, w1, of that line bundle.
Stiefel-Whitney classes obey the following four axioms.
1. For every real line bundle E → X, there exists wi(E) in Hi(X, Z/2Z) which are natural, in other words, f*wi(E) = wi(f*E) for any continuous map between spaces.
2. w0(E) = 1 in H0(X; Z/2Z)
3. Normalization condition: wi(γ1) = x in H1(RP1; Z/2Z) = Z/2Z, where γn is the canonical line bundle.
4. Whitney product formula:
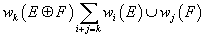
wk(E + F) = [summation over i + j = k] wi(E) ∪ wj(F)
The Chern classes can be used to construct a homomorphism of rings from the topological K-theory of a space to the completion of its rational cohomology. For line bundles V, the Chern character ch is defined by
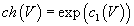
ch(V) = exp(c1(V))
For sums of line bundles, the Chern character is defined by addivity. For arbitrary vector bundles, it is defined by pretending that the bundle is a sum of line bundles. For sums of line bundles, the Chern character can be expressed in terms of Chern classes, and we use the same formulas to define it on all vector bundles. For example, the first few terms are
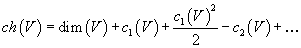
ch(V) = dim(V) + c1 + c1(V)2/2 – c2(V) + ...
If V is filtered by line bundles L1, L2,...Lk having first Chern classes x1, x2,...xk respectively, then
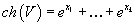
ch(V) = ex1 + ex2 +...+exk
If the connection is used to define the Chern classes, then the explicit form of the Chern character is
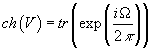
ch(V) = tr(exp(iΩ/2π))
where Ω is the curvature of the connection.
The Chern character is useful partly because you can use it to compute the Chern class of a tensor product. Specifically, it obeys
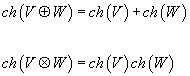
ch(V + W) = ch(V) + ch(W)
ch(V x W) = ch(V) ch(W)
Using the Grothendieck addivity axiom for Chern classes, the first of these identities can be generalized to a state where ch is a homomorphism of abelian groups from the K-theory K(X) into the rational cohomology of X. The second identity establishes the fact that this homomorphism also respects products in K(X), and so ch is a homomorphism of rings.
The Steenrod algebra has to do with the cohomology operations in singular cohomology with integer mod 2 coefficients. For every n ∈ Z, and i ∈ {0, 1, 2, 3,...}, there are natural transformations of functors
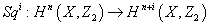
Sqi : Hn(X, Z2) → Hn + i(X, Z2)
satisfying the following axioms.
1. Sqi = 0 for i > n
2. Sqn(X) = X ∪ X for all X ∈ Hn(X, A; Z2) and all pairs (X, A)
3. Sq0 = idHn(X, Z2)
4. The Sqi maps commute with the coboundary maps in the long exact sequence of a pair. In other words
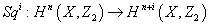
Sqi : Hn(X, Z2) → Hn + i(X, Z2)
is a degree i transformation of cohomology theories.
5. Cartan relations:
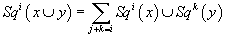
Sqi(x ∪ y) = [summation over j + k = i] Sqi (x) ∪ Sqk(y)
6. Adem relations:
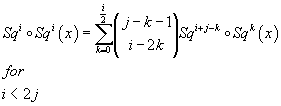
Sqi o Sqi(x) = [summation over k from 0 to i/2] (j – k – 1 i – 2k) Sqi + j – k o Sqk(x), for i < 2j
7.
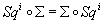
Sqi o Σ = Σ o Sqi
Where Σ is the cohomology suspension isomorphism.
The existence of these cohomology operations endows the cohomology ring with the structure of a module over the Steenrod algebra A, defined to be T(FZ2 {Sqi : i ∈ {0, 1, 2, 3,...}})/R where FZ2(x) is the free module functor that takes any set, and sends it to the free Z2 module over that set. We think of FZ2 {Sqi : i ∈ {0, 1, 2, 3,...}} as being a graded Z2 module, where the ith gradation is given by Z2 . Sqi. This makes the tensor algebra T(FZ2 {Sqi : i ∈ {0, 1, 2, 3,...}}) into a graded algebra over Z2. R is the ideal generated by the elements
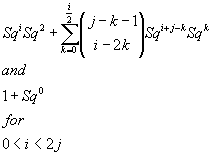
Sqi Sq2 + [summation over k from 0 to i/2] Sqi + j – k Sqk and 1 + Sq0 for 0 < i < 2j
This makes A into a graded Z2 algebra.
By the definition of the Steenrod algebra, for any space (X, A), Hn(X, A; Z2) is a module over the Steenrod algebra A, with multiplication induced by Sqi . x = Sqi(x). Therefore, cohomology with coefficients in the ring Z2, Hn(X, Z2) is a functor from the category of pairs of topological spaces to graded modules over A.