In superstring theory, K-theory is conjectured to classify the allowed Ramond-Ramond field strengths, and also the charges of stable D-branes. This conjecture was first proposed in 1997 by Ruben Minasian and Gregory Moore in their paper "K-theory and Ramond-Ramond charge". It was popularized by Edward Witten in his paper "D-branes and K-theory" where he demonstrated that in Type IIB string theory, it arises naturally from Ashoke Sen's realization of arbitrary D-brane configurations as stacks of D9-branes and anti-D9-branes after tachyon condensation. Such stacks of branes are inconsistent in a non-torsion Neveu-Schwarz (NS) 3-form background which, as was pointed out by Anton Kaputsin, complicates the extension of K-theory classification to such cases. Peter Bouwknoght and Mathai Varghese suggested a solution to this problem. D-branes are in general classified by twisted K-theory which had been defined in 1989 by Jonathan Rosenberg.
The K-theory classification of D-branes has numerous applications. For instance, Amihay Hanany and Barak Kol used it to argue that there are eight species of orientifold one-plane. Angel Urganga applied the K-theory classification to derive new consistency conditions for flux compactification. K-theory has also been used to conjecture a formula for the topologies of T-dual manifolds. Recently, K-theory has been conjectured to classify the spinors in compactifications on generalized complex manifolds.
Despite these successes, RR fluxes are not quite classified by K-theory. In their paper "In E8 Gauge Theory and a Derivation of K-theory from M-theory", Emanuel Diaconescu, Gregory Moore, and Edward Witten (DMW) argued that the K-theory classification is incompatible with S-duality in Type IIB string theory. Another problem is that if you try to classify the fluxes on a compact ten-dimensional spacetime, then a complication arises due to the self-duality of the RR fluxes. The duality uses the Hodge star, which depends on the metric, and so is continuously valued, and thus usually irrational. Therefore, not all the RR fluxes, which are interpreted as Chern characters in K-theory, can be rational. However, Chern characters are always rational. You have to choose half the fluxes to quantize, or a polarization in the geometric quantization inspired language of DMW, and later Mathai Varghese and Hisham Sati. You could also use the K-theory of a 9-dimensional time slice, as was done by Juan Maldacena and Nathan Seiberg.
In the classical limit of Type II string theory, which is Type II supergravity, the Ramond-Ramond field strengths are differential forms. In the quantum theory, the well-definedness of the partition functions of D-branes implies that the RR field strengths obey Dirac quantization conditions when spacetime is compact, or when a spatial slice is compact, and you consider only the magnetic components of the field strength which lies along the spatial directions. This led 20th Century physicists to classify RR field strengths using cohomology with integer coefficients.
However, some authors have argued that the cohomology of spacetime with integer coefficients is too large. For example, in the presence of Neveu-Schwarz H-flux or non-spin cycles, some RR fluxes dictate the presence of D-branes. In the former case, this is a consequence of the supergravity equation of motion which states that the product of an RR-flux with the NS 3-form is a D-brane charge density. Thus the set of topologically distinct RR field strengths that can exist in brane-free configurations is only a subset of the cohomology with integer coefficients. This subset is still too big because some of these classes are related by gauge transformations. In QED, there are gauge transformations which add integer multiples of 2π to Wilson loops. The p-form potentials in Type II supergravity theories also have these large gauge transformations but due to the presence of Chern-Simon terms in supergravity actions, these gauge transformations transform not only the p-form potentials but also the (p + 3)-form field strengths. Thus to obtain the space of inequivalent field strengths from the subset of integral cohomology, we must quotient these by the gauge transformations.
The Atiyah-Hirzebruch spectral sequence constructs twisted K-theory, with the twist given by the NS 3-form field strength, as a quotient of a subset of the cohomology with integer coefficients. In the classical limit, which corresponds to working with rational coefficients, this is precisely the quotient of the subset described above with supergravity. The quantum corrections come from torsion classes and contain mod 2 torsion corrections due to the Freed-Witten anomaly.
Twisted K-theory classifies the subset of RR field strengths that can exist in the absence of D-branes quotiented by large gauge transformations. Daniel Freed has attempted to extend this classification to include the RR potentials using differential K-theory.
K-theory classifies D-branes in noncompact spacetimes, intuitively in spacetimes in which we are not concerned about the flux sourced by the brane having nowhere to go. While the K-theory of a 10d spacetime classifies D-branes as a subset of that spacetime, if the spacetime is the product of time and a fixed 9-manifold, then K-theory also classifies the conserved D-brane charges on each 9-dimensional spatial slice. While we are required to forget about the RR potentials to obtain the K-theory classification of RR field strengths, we are required to forget about the RR field strengths to get the K-theory classification of D-branes.
Petr Horava pointed out that K-theory classification of D-branes is independent of, and in some ways stronger than, the classification of BPS states. K-theory appears to classify stable D-branes that are missed by supersymmetry based classifications. For example, D-branes with torsion charges, meaning charges in the order N cyclic group ZN, attract each other, and so can never be BPS. In fact, N such D-branes can decay, while no superposition of branes that satisfy a Bogomolny bound can ever decay. However, the charge of such branes is conserved modulo N, and this is captured by the K-theory classification but not a BPS classification. Such torsion branes have been applied, for example, to model Douglas-Shenker strings in supersymmetric U(N) gauge theories.
Ashoke Sen has conjectured that in the absence of a topologically nontrivial NS 3-form, all Type IIB brane configurations can be obtained from stacks of space filling D9 and anti-D9 branes via tachyon condensation. The topology of the resulting branes is encoded in the topology of the resulting gauge bundle on the stack of the space filling branes. The topology of the gauge bundle on a stack of D9s and anti-D9s can be decomposed into a gauge bundle on the D9s, and another gauge bundle on the anti-D9s. Tachyon condensation transforms such a pair of bundles into another pair in which the same bundle is direct summed with each component of the pair. Thus the tachyon condensation invariant quantity, which is the charge which is conserved in the tachyon condensation process, is not a pair of bundles but is instead an equivalence class of a pair of bundles under the direct sum of the same bundle on both sides of the pair. This is precisely the usual construction of topological K-theory. Thus the gauge bundles on stacks of D9s and anti-D9s are classified by topological K-theory. According to Sen's conjecture, all D-brane configurations in Type IIB are then classified by K-theory. Petr Horova has extended this extended this conjecture to Type IIA using D8-branes.
While the tachyon condensation picture of K-theory classification classifies D-branes as subsets of a 10-dimensional spacetime with no NS 3-form flux, the Maldacena, Moore, Seiberg picture classifies stable D-branes with finite mass as subsets of a 9-dimensional spatial slice of spacetime. The main point is that D-branes are not classified by integral cohomology because Dp-branes wrapping certain cycles suffer from a Freed-Witten anomaly which is cancelled by the insertion of D(p - 2)-branes, and sometimes D(p - 4)-branes, that end on the Dp-brane. These inserted branes may either continue to infinity, in which case the composite object has infinite mass, or they may end on an anti-Dp-brane, in which case the total Dp-brane charge is zero. In either case, you would probably want to remove the anomalous Dp-branes from the spectrum leaving only a subset of the original integral cohomology. The inserted branes are unstable. To see this, imagine that they extend in time into the past, away from the anomalous brane. This corresponds to a process in which the inserted branes decay via a Dp-brane that forms, wraps around the cycle, and then disappears. Maldacena, Moore, and Seiberg refer to this process as an instanton, although it doesn't have to be instantonic. The conserved charges are thus the nonanomalous subset quotiented by the unstable insertions. This is precisely the Atiyah-Hirzebruch spectral sequence construction of twisted K-theory as a set.
Diaconescu, Moore, and Witten (DMW), have pointed out that the twisted K-theory classification is not compatible with S-duality covariance in Type IIB string theory. For example, here you have the 3-form field strength G3 in the Atiyah-Hirzebruch spectral sequence (AHSS)
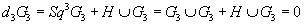
d3G3 = Sq3G3 + H ∪ G3 = G3 ∪ G3 + H ∪ G3 = 0
where d3 = Sq3 + H is the first nontrivial differential in the AHSS, Sq3 is the third Steenrod square, and the last equality follows from the fact that the n-th Steenrod square acting on any n-form x is x ∪ x. The above equation is not invariant under S-duality which exchanges G3 and H. Instead, DMW have proposed the following S-duality covariant extension
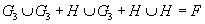
G3 ∪ G3 + H ∪ G3 + H ∪ H = F
Where F is an unknown characteristic class that depends only on the topology, and not on the fluxes. Diaconescu, Freed, and Moore wrote a paper titled, "The M-theory 3-form and E8 Gauge Theory" in which they found a constraint on F using the E8 gauge theory approach to M-theory pioneered by DMW. Thus D-branes in Type IIB are not classified by twisted K-theory after all, but by some unknown S-duality covariant object that also classifies both fundamental strings and NS5-branes.
The method of calculating twisted K-theory invented by Maldacena, Moore, and Seiberg (MMS) can also easily S-covariantized since the Freed-Witten anomalies respect S-duality. Thus the S-covariantized form of the MMS construction can be applied to construct the S-covariantized twisted K-theory, as a set, without knowing what the S-covariantized object is. This program has been carried out in a number of papers, and has been applied to fluxes, and has been used to prove DMW's conjectured constraint on 3-fluxes, and they show there is an additional term equal to the D-brane charge. The Klebanov-Strassler cascade of Seiberg dualities consists of a series of S-dual MMS instantons, one for each Seiberg duality. The group ZN of universal classes of the SU(M + N) x SU(M) supersymmetric gauge theory is then shown to agree with the S-dual twisted K-theory, and not with the twisted K-theory.
So basically, we started with K-theory, and because the cohomology of spacetime with integer coefficients was too large, we moved to twisted K-theory, and then because it was inconsistent with S-duality in Type IIB theory, we moved to S-covariantized twisted K-theory. Hisham Sati and Igor Kriz propose that instead of using any type of twisted K-theory at all, we should instead classify Type II string theory configurations using elliptic cohomology.
Let me illustrate how to apply some of the ideas we've discussed to string theory. Let's say you have Type I string theory on R10. Let's look at the following homotopy group of SO(32).
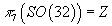
π7(SO(32)) = Z
SO(32) bundles on the (i + 1)-dimensional sphere Si + 1 are classified by πi(SO(32)). SO(32) bundles on Si + 1 are equivalent to SO(32) bundles on Euclidean space RI + 1 that are trivialized at infinity, meaning that the pure gauge at infinity and the action integral on Ri + 1 converges. So you can use π7 to construct strings.
The string associated with π7(SO(32)), called a gauge string, can be identified as follows. Let B be the two-form field of Type I superstring theory. It is a Ramond-Ramond field and couples to the D-string. However, B also couples to the gauge string because of the Green-Schwarz anomaly canceling term
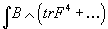
∫ B ∧ (tr F4 + ...)
since the gauge string is made from a gauge field on R8 with nonzero integral
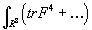
∫R8 (tr F4 + ...)
The minimal gauge string has D-string charge ±1. This suggests that the string constructed in low energy field theory using a generator of π7(SO(32)) shrinks dynamically to an ordinary D-string.
To compute the D-string charge of the gauge string, let V be an SO(32) bundle on R8 with a connection of finite action. Because the connection is flat at infinity, we can compactify and regard V as an SO(32) bundle on S8. This bundle has first Pontryagin class p1(V) = 0 since p1(V) would take values in H4(S8) which vanishes and
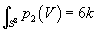
∫S8 p2(V) = 6k
where k is an arbitrary integer. The factor of 6 arises as follows. The topological charge of an SO(32) bundle V on S8 is measured by the Dirac index, which, depending on the choice of V, can be an arbitrary integer k. However, using the index theorem, the Dirac index for spinors on S8 valued in V is
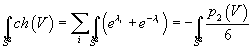
[integral over S8] ch(V) = [summation over i] [integral over S8] (eλi + e-λi) = -[integral over S8] p2(V)/6
where λi are the roots of the Chern polynomial, the Pontryagin classes are
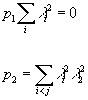
p1 [summation over i] λi2 = 0
p2 = [summation over i < j] λ12 λ22
and ch is the Chern character. Therefore p2(V) can be any multiple of 6.
At the same time, the standard anomaly twelve-form, which is the one loop anomaly of the massless gravitinos and gluinos of the Type I theory, is
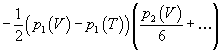
-½(p1(V) - p1(T))(p2(V)/6 +… )
Since the field strength H of the B-field, normalized so that the periods of B are multiples of 2π,obeys
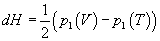
dH = ½(p1(V) - p1(T))
the properly normalized coupling of B to p2(V) is
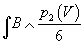
∫ B ∧ p2(V)/6
since p2(V)/6 can be any integer, it follows that the minimal gauge string has D-string charge 1, and thus can be identified with the D-string.
In string theory, you are often concerned with the stability of D-branes and this has to do with how D-branes can wrap around the compactified dimensions, called cycles, and also the charges of the D-branes, such as the Neveu-Schwarz charge H, or Ramond-Ramond charge F. Also, you have to consider the possibility that a brane and antibrane could annihilate. Let's say, with Type II string theory, you have a p-brane and an anti-p-brane, written [p bar]-brane, both wrapped around the same submanifold W of a spacetime X. In this case, the p-brane and anti-p-brane could annihilate. You have open strings with both ends on the p-brane, called p-p strings, open strings with one end on the p-brane and the other end on the anti-p-brane, called p-[p bar] strings, and finally open strings with both ends on the anti-p-brane, called [p bar]-[p bar] strings. The p-p open string spectrum consists of a massless super-Maxwell multiplet plus massive excitations. The familiar NS sector tachyon is removed by the GSO projection. The [p bar]-[p bar] open strings give another super-Maxwell multiplet. However, for p-[p bar] and [p bar]-p open strings, you have to make the opposite GSO projection. Therefore, the massless vector multiplet is projected out, and the tachyon survives. The fact that you are left with a tachyon after GSO projection means that the system is unstable, and what that means is that the brane and antibrane would annihilate each other. The instability associated with the tachyon represents a flow towards annihilation of the brane-antibrane pair. By giving the tachyon field a suitable excitation value, you can return to the vacuum state without the brane-antibrane pair.
The gauge group on the brane-antibrane pair is U(1) x U(1), with one U(1) on the brane, and the other U(1) on the antibrane. The tachyon field T has charges (1, -1), and its expectation value breaks U(1) x U(1) to a diagonal U(1) subgroup. This U(1) must ultimately be eliminated in the brane-antibrane annihilation.
The fact that the p-[p bar] and [p bar]-p strings have a reversed GSO projection can be explained as follows. Let's say you have a p-[p bar] brane system, and it has a Chan-Paton label i, where i = 1 for an open string ending on a p-brane, and i = 2 for an open string ending on a [p bar]-brane. So therefore, you have an open string, and at each end of the open string, you have a charge that takes values in a two-dimensional Hilbert space. Let's say the i = 1 state is bosonic, and the i = 2 state is fermionic. Then the GSO operator, (-1)F, which usually acts trivially on the Chan-Paton factors, here acts by
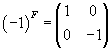
The p-p and [p bar]-[p bar] open strings have diagonal Chan-Paton wavefunctions. The wavefunctions are even under (-1)F, leading to the usual GSO projection on the oscillator modes. The Chan-Paton wavefunctions for the p-[p bar] and [p bar]-p open strings are off-diagonal, and odd under (-1)F, leading to a reversed GSO projection. If you were to multiply the above equation by an overall factor of -1, in the action of (-1)F on string states, it would cancel out since each open string has two ends.
Having one bosonic and one fermionic Chan-Paton state would lead, if we made no GSO projection, to a gauge supergroup U(1|1). Because of the GSO projection, the off-diagonal fermionic gauge fields of U(1|1) are absent, so we instead get a structure whose lowest modes correspond to a superconnection, which is a matrix of the form
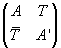
where A and A' are the gauge fields, and T is the p-[p bar] tachyon. If E and F are bundles of bosonic and fermionic Chan-Paton states respectively, and A and A’ are connections on E and F, then T is a section of E ⊗ F*, and [T bar] is a section of E* ⊗ F, where E* is the dual of the bundle of E.
Now let's consider a more general case with n p-branes and n [p bar]-branes wrapped on the submanifold W of spacetime. We allow an arbitrary U(n) gauge bundle E for the p-branes, and topologically the same bundle for the [p bar]-branes. The reason for having the same gauge bundle for both branes and antibranes is to make sure the overall system carries no D-brane charge. The operator (-1)FL maps p-branes to [p bar]-branes, and reverses the sign of all D-brane charges, while leaving fixed the gauge fields on the branes. Since there is no conserved charge, there is a tachyon field in the p-[p bar] sector, and you would expect any such system of branes to annihilate.
Now, let's first specialize to the case of Type IIB superstrings, and secondly, we will use only 9-branes and anti-9-branes. We start with an arbitrary number of n 9-branes, and the same number of anti-9-branes. The reason we require the same number of 9-branes and anti-9-branes is so we have tadpole cancellation. In general, the 9-branes carry a U(n) gauge bundle E, and the [9 bar]-branes carry a U(n) gauge bundle F. We will label this configuration by the pair (E, F). What other configurations (E', F') is the configuration (E, F) equivalent to? The basic equivalence relation is brane-antibrane creation and annihilation. Any collection of m 9-branes and m [9 bar]-branes, with the same U(m) gauge bundle H for both branes and antibranes, can be created and annihilated. So the pair (E, F) can be smoothly deformed to

(E ⊕ H, F ⊕ H)
Since we are only interested in keeping track of conserved D-brane charges, properties that are invariant under smooth deformations, we consider the pair (E, F) to be equivalent to
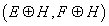
(E ⊕ H, F ⊕ H)
What we have arrived at is the definition of the K-group K(X), which is defined by saying that an element of K(X) is a pair of complex vector bundles (E, F) over spacetime, subject to an equivalence relation which is generated by saying that (E, F) is equivalent to (E ⊕ H, F ⊕ H) for any H. K(X) is a group, the sum of (E, F) and (E', F') being
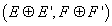
(E ⊕ E', F ⊕ F')
It's actually a ring with the product of (E, F) and (E', F') being
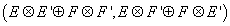
(E ⊗ E' ⊕ F ⊗ F', E ⊗ F' ⊕ F ⊗ E')
as if the E's were bosonic, and the F's fermionic.
(E, F) can be written E - F. The subgroup of K(X) consisting of elements such that E and F have the same rank, meaning having equal numbers of 9-branres and [9 bar]-branes, is usually called [K tilde](X).
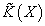
Therefore, tadpole canceling 9-[9 bar] configurations, modulo creation and annihilation of brane-antibrane pairs, are classified by [K tilde](X).
The spacetime X is usually noncompact, such as X = R4 x M, where M is compact. Because of a finite action or finite energy restriction, you want objects that are equivalent to the vacuum at infinity. This means that near infinity, you can relax to the vacuum by tachyon condensation. If there are no branes in the vacuum, then in the pair (E, F), E is isomorphic to F.
In general, the vacuum may contain branes, and this may be represented by a nonzero K-theory class. Tadpole cancellation, meaning that the condition that the equations of motion of Ramond-Ramond fields should have solutions, typically determines the K-theory class of the vacuum in terms of K-theory data. Requiring that the class (E, F) is equivalent to the vacuum, we get a K-theory class (E', F') that is trivial at infinity, in the sense that E' and F' are isomorphic at infinity. The Ramond-Ramond charge of an excitation of a given vacuum is best measured by subtracting the K-theory class of the vacuum from its K-theory class. Therefore in the most physical applications, the Ramond-Ramond charge of an excitation of the vacuum is considered to take values not in the ordinary K-group K(X) but in K-theory with compact support. A K-theory class with compact support is always represented by a pair of bundles of equal rank, since bundles that are isomorphic at infinity have equal rank. Therefore, the distinction between K(X) and [K tilde](X) is not important for most physical applications.
Up until now, we've been discussing Type IIB theory. Let's now address Type I and Type IIA. For Type I theory, let's say you have a system of n 9-branes, and m [9 bar]-branes. Tadpole cancellation says that n - m = 32. The branes support an SO(n) bundle E and an SO(m) bundle F. By brane-antibrane creation and annihilation, we assume that the pair (E, F) is equivalent to (E ⊕ H, F ⊕ H) for any SO(k) bundle H. Pairs (E, F) with this equivalence relation define the real K-group of spacetime, written KO(X). The subgroup with n - m = 0 is called [KO tilde](X). Any configuration with n - m = 32 can be naturally mapped to [KO tilde](X) by adding to F a rank 32 trivial bundle. Therefore, pairs (E, F) subject to the equivalence relation, and with n - m = 32, are classified by [KO tilde](X). You want to measure the K-theory class of an excitation relative to the vacuum, so then the brane charge of an excitation is measured by [KO tilde](X) with a compact support condition. If you have a compact support condition, KO(X) and {KO tilde](X) are equivalent, so you can say that 9-[9 bar] configurations in Type I are classified by KO(X). Unlike the situation in Type IIB, the identification of 9-brane configurations in Type I with KO-theory does not require assumptions about brane-antibrane annihilation. Since X has dimension 10, the classification of SO(32) bundles on X is governed by the homotopy groups πi(SO(32)) for i ≤ (, and the relations between them. These homotopy groups are in the stable range, and the SO(32) bundles on X are classified by [KO tilde](X).
Now, I'll briefly discuss Type IIA theory. Here you relate branes not to bundles on X but to bundles on X x S1. This might be related to the circle used in relating Type IIA to M-theory. Given a p-brane wrapped on an odd-dimensional submanifold Z ⊂ X, we identify Z with a submanifold Z'= w x Z in X x S1, where w is any point in S1. Z' has even codimension in X x S1. A brane wrapped on Z' determines an element of K(X x S1). This element is trivial when restricted to X, meaning w' x X for any w ∈ S1. Two Type IIA brane configurations on X are equivalent if they determine the same element of K(X x S1). The subgroup of K(X x S1) consisting of elements that are trivial on X is called K'(X). By Bott periodicity, K(X) and K'(X) are the only complex K-groups of X. Therefore, we have two K-groups and two Type II string theories, so you have one K-group for each Type II string theory. For application to Type IIA, you need the subgroup [K tilde]'(X) = [K tilde](X x S1) since we have no physical interpretation of 10-branes wrapping X x S1. Therefore, D-brane charges in Type IIA are classified by K’(X) with an appropriate compact support condition.
Up until now, we've been talking about a stack of 9-branes and anti-9-branes. However, according to Sen's conjecture, any p-brane with p ≤ 9 is equivalent to a stack of 9-branes and anti-9-branes. What that means is that the charge of any p-brane of any dimension can be classified by K-theory. I will now briefly review Sen's construction of a p-brane as a bound state of a (p + 2)-brane and a coincident (p + 2)-antibrane. We'll work in R10 so you don't have to worry about the effects of spacetime topology. Let’s say you have an infinite (p + 2)-brane-antibrane pair stretching over RP + 3 ⊂ R10. One the brane-antibrane pair, there is a U(1) x U(1) gauge field with a tachyon field T of charges (1, -1). Let's say you have a vortex in which T vanishes on a codimension two subspace RP + 1 ⊂ Rp + 3 which will be interpreted as a p-brane worldvolume. Let's say T approaches its vacuum expectation value at infinity up to a gauge transformation. Since T is a complex field, it can have a winding number around the codimension two locus on which it vanishes, or equivalently at infinity, where the basic case is that the winding number is 1. T breaks U(1) x U(1) to U(1). To keep the energy per unit p-brane volume finite, there must be a unit of magnetic flux in the broken U(1). Because of this magnetic flux, the system has a p-brane charge of 1. It's (p + 2)-brane charge cancels, of course, between the brane and antibrane. With the tachyon close to the vacuum expectation value, expect at the vortex, the system looks like vacuum everywhere, except near the locus where T vanishes. Since this locus carries unit p-brane charge, it can be interpreted as a p-brane. In other words, a p-brane can be viewed as a (p + 2)-brane-antibrane pair.
So how would you then generalize this to interpret a p-brane as a configuration of (p + 2k)-branes and antibranes with k < 1? One way is to repeat what we just did k times. We first make a p-brane as a bound state of a (p + 2)-brane and antibrane. Then let's say each of those (P + 2)-brane-antibrane pairs is made from a (p + 4)-brane-antibrane pair. Therefore, we have a p-brane built from two (p + 4)-brane-antibrane pairs. After k - 2 more steps, we have a p-brane built from 2k - 1 pairs of (p + 2k)-branes and antibranes. To exhibit the symmetries more fully, it would be better to do the construction all at once instead of stepwise. Let's say you have a general collection of n (p + 2k)-brane-antibrane pairs. The branes carry U(n) x U(n) gauge symmetry under which the tachyon field T transforms as (n, [n bar]). In vacuum, T breaks U(n) x U(n) down to a diagonal U(n). To make a p-brane, we want T to vanish in codimension 2k, on an Rp + 1 ⊂ Rp + 2k + 1, and to approach its vacuum orbit at infinity with a nontopological twist around the locus on which T vanishes. Such configurations are classified topologically by π2k - 1(U(n)). According to Bott periodicity, this group equals Z for sufficiently large n. This copy of Z will label the possible values of p-brane charge.
Let S+ and S- be the positive and negative chirality spinor representation of SO(2k). They are of dimension 2k - 1. Let
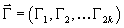
Γ = (Γ1, Γ2,...Γ2k)
be the usual gamma matrices regarded as maps from S- to S+. If x = (x1, x2,...x2k) is an element of S2k – 1, meaning a 2k-vector with x2 = 1, then we define the tachyon field by
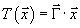
T(x) = Γ . x
It has winding number 1, and generator π2k – 1(U(2k – 1)). The p-brane charge is 1, and all higher and lower charges vanish. Since this configuration has p-brane charge 1, and looks like the vacuum except near x = 0, we assume that this is, in fact, a p-brane.
So therefore, a p-brane is equivalent to 2k – 1 pairs of (p + 2k)-branes and antibranes. So therefore, a 1-brane is the same as 24 - 1 = 23 = 8 pairs of (1 + 2(4)) = (1 + 8) = 9-branes and antibranes. A 3-brane is the same as 23 - 1 = 22 = 4 pairs of (3 + 2(3)) = (3 + 6) = 9-branes and antibranes. A 5-brane is the same as 22 - 1 = 21 = 2 pairs of (5 + 2(2)) = (5 + 4) = 9-branes and antibranes. A 7-brane is the same as 21 - 1 = 20 = 1 pair of (7 + 2(1)) = (7 + 2) = 9-branes and antibranes. A 9-brane, of course, is already a 9-brane. Since string theory is 10-dimensional, you can’t have an odd-dimensioned p-brane higher than a 9-brane. So any odd-dimensional p-brane is equivalent to a collection of 9-branes and antibranes. Since the charges of any number of pairs of 9-branes and antibranes can be classified by K-theory, therefore the charges of any odd-dimensional p-brane can also be classified by K-theory.
A D-brane wrapped on a submanifold S of spacetime may carry a nonzero Ramond-Ramond (RR) charge. D-branes carry gauge fields, and these fields are natural in K-theory, which has been used to answer some questions about RR charges and fields.
If X is spacetime, and A(X) is the commutative associative algebra of continuous complex-valued functions on X, then the K-theory of X can be defined in terms of representations of A(X). A representation of a ring is called a module. The most obvious example of an A(X)-module is A(X) itself. For f ∈ A(X), regarded as a ring, and g ∈ A(X), regarded as a module, you have f(g) = fg, where on the right hand side, the multiplication occurs in A(X). This obeys the defining condition of a module which is (f1 f2)(g) = f1(f2(g)).