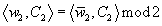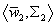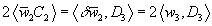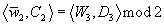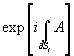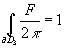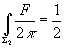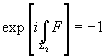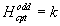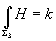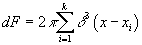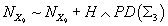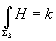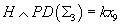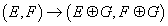
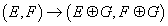
(E, F) → (E ⊕ G, F ⊕ G)
The equivalence classes make up a group called K(X). You could call it K(A(X)) if you want to emphasize the interpretation in terms of A(X)-modules. D-branes in Type IIB carry conserved charges that take values in K(X).
Whenever you look closely at topological properties of RR charges or fields, you see effects that reflect the K-theory structure. For example, there are stable D-brane states, such as the nonsupersymmetric D0-branes of Type I, that would not exist if D-brane charge were classified by conventional cohomology instead of K-theory. Also, it is possible to have a D-brane state that would be stable if D-brane charge were measured by conventional cohomology, but are in fact unstable due to a process that involves nucleation of D9-[D9 bar] pairs in an intermediate state. This occurs in Type II superstring theory in which a D-brane wrapped on a homologically nontrivial cycle in spacetime is in fact unstable. Also, the K-theory interpretation of D-branes is needed to explain a global worldvolume anomaly.
K-theory can be naturally adapted to stringy generalizations. We defined K(X) in terms of representations of the algebra A(X) of functions on spacetime. We could also define K(A) for any noncommutative algebra A in terms of pairs (E, F) of A-modules. Turning on the Neveu-Schwarz B-field, you can make A(X) noncommutative. The associated K(A) was used by Connes, Douglas, and Schwarz in the original paper on noncommutative Yang-Mills theory applied to string theory. It would be great to have a fully stringy version involving a noncommutative algebra constructed using all the modes of the string, not just the zero modes. One possible candidate for the noncommutative algebra is the *-algebra of open string field theory, defined in terms of gluing strings together. If you call this algebra Ast, it seems plausible that D-brane charge is naturally labeled by K(Ast). For a manifold of large volume compared to the string scale, K(Ast) is the same as ordinary K(X) of topological K-theory.
An RR p-form field Gp obeys a Dirac quantization law according to which, for any p-cycle U in spacetime
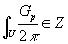
∫U Gp/2π ∈ Z
meaning, is an integer. The actual quantization conditions on RR periods are more subtle than the above equation. There are a variety of corrections to the above equation that involve spacetime curvature and gauge fields on the brane, such as self-duality and global anomalies.
For Type IIB superstrings, it turns out that RR fields are classified by K’(X). For our purposes, K’(X) can be defined as the group of components of the group of continuous maps from X to U(N) for any sufficiently large N, where N is the number of D-branes. This means that topological classes of RR fields on X are classified by a map U: X → U(N) for some large N. The relation of Gp to U is Gp ~ Tr(U-1 dU)p, ignoring corrections due to spacetime curvature and the self-duality of the RR fields. We don’t know what U actually is. This is analogous to the fact that RR fields are classified by U(N) gauge bundles, for some large N, with connection A and curvature FA, where Gp ~ Tr FAp/2. M-theory involves E8 gauge bundles with connection. We don’t really know the physical meaning of the U(N) gauge bundles or the E8 gauge fields.
Using K’(X) to classify RR fields in Type IIB gives you a way to summarize very complicated quantization conditions obeyed by the RR fields. In addition, this framework is useful in describing subtle phase factors that enter into the RR partition function. When it became known that RR charges were classified by K-theory, people at that time should have immediately realized that RR fields were also classified by K-theory, since RR charges produce RR fields, but it tool a couple of years for people to realize this.
Just like K0(X), K1(X) has an analog for any noncommutative algebra A. Given A, you let AN denote the group of invertible N x N matrices whose matrix elements are elements of A. Then K’(X) is the group of components of AN for large N. For example, if A = A(X) is the ring of complex-valued continuous functions on X, then AN is the group of maps of X to GL(N, C). This is contractible to the group of maps of X to U(N), so for large N, the group of components of AN is the same as K’(X). The existence of a generalization of K’(X) in the long distance limit might be a useful starting point for stringy generalizations.
Up until now, we’ve assumed that N, the number of D-branes, was a sufficiently large but finite integer. What happens if you set N equal to infinity? There are many examples in string theory where we study the N → ∞ limit. Examples include the conjectured link between strings and gauge theory, the old matrix models that are used to give solvable examples of string theory, the matrix model of M-theory, and the correspondence between gravity in an asymptotically AdS spacetime and conformal field theory (AdS/CFT correspondence). In the present case, it is worthwhile to study D-branes with N = ∞, with tachyon condensation to annihilate most of the branes and reduce it to something more manageable. One question is the relation of Type IIA superstrings to K-theory. Another is the inclusion of a nontrivial topological NS three-form H in the K-theory classification of RR charges and fields.
For Type IIB superstrings, we used K0(X) to classify RR charges, and K1(X) to classify RR fields. Therefore, because of T-duality, it should be reversed for Type IIA superstrings. According to T-duality, for Type IIA superstrings, K1(X) should classify RR charges, and K1(X) should classify RR fields. By Bott periodicity, Ki + 2(X) = Ki(X), so the only K-groups of X are K0(X) and K1(X). In 1999, Petr Horova came up with the best explanation of why K1(X) classifies RR charges in Type IIA. Let’s say you have a system of N unstable D9-branes in Type IIA. The branes support a U(N) gauge field and a tachyon field T in the adjoint representation of U(N). There is a symmetry T → -T. The effective potential of the tachyon field has the general form
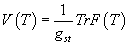
V(T) = (1/gst) Tr F(T)
where the function F(T) is non-negative, and after scaling T correctly, vanishes precisely if T = ±1. Therefore, V(T) is minimized if and only if every eigenvalue of T = ±1. Horova argued that in flat R10, you can make supersymmetric Dp-branes, for even p, as solitons of T. For instance, to make a D6-brane, you set N = 2. Let x be the three coordinates normal to the D6-brane, and set
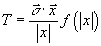
T = ((σ . x)/| x | )f(|x|)
Where f(r) ~ r for small r, and f(r) → ∞ for r → ∞. Then for | x | → ∞, the eigenvalues of T are everywhere ±1. Near x = 0, there is a topological knot that can be interpreted as a D-brane.
In flat R10, you can make Dp-branes for other even p the same way. You can do it on flat spacetime for any value of N, but you can only do it on curved spacetime if N is equal to infinity. On a general spacetime, this does not work for arbitrary Dp-branes unless you set N = ∞. The problem is most obvious if X, or at least its spatial part, is compact. The tachyon field T, being adjoint-valued, maps X to the Lei algebra of U(N). Since the Lie algebra is contractible, T carries no topology. A map from X to the Lie algebra does not represent an element of K’(X). Since it can be contracted to a point, it carries no topological information.
Therefore, to define an element of K’(X), you need a group, not the Lie algebra. You use the map U : X → U(N). What’s amazing is that if you set N = ∞, you get the correct topology from the Lie algebra. You have to interpret U(∞) to be the unitary group U of a Hilbert space H of countable infinite dimension, which is called a separable Hilbert space. You interpret the N = ∞ analog of the space of hermitian N x N matrices to be the space of bounded self-adjoint operators T on H whose spectrum is as follows. There are infinitely many positive eigenvalues and infinitely many negative eigenvalues. Zero is not an accumulation point on the spectrum which makes T into a Fredholm operator. Physically, T should be required to obey these conditions since they are needed to make the energy and D8-brane charge finite. To make the energy finite, almost all the eigenvalues of T are very close to ±1. With these conditions imposed on T, it turns out that the space of T has the same topology as that of U(N) for large N.
Therefore, you can use tachyon condensation on a system of D9-branes to describe RR charges for Type IIA but you have to start with infinitely many D9-branes which then undergo tachyon condensation down to a configuration of finite energy.
We also want to consider D9-branes when the Neveu-Schwarz three-form H is nontrivial. Just as with H= 0, we want to classify D-brane states by pairs (E, F), when E is a D9-brane, and F is an anti-D9-brane, subject to the usual equivalence relations. However, there is a problem with having a D9-brane in the presence of a Neveu-Schwarz H-field. When H is topologically nontrivial, you can’t have a single D9-brane. On the D9-brane, there is a U(1) gauge field with field strength F. The relation dF = H shows that H must be topologically trivial if a single D9-brane is present. This is most easily shown in de Rham cohomology, but it’s true generally.
Now let’s consider the case where we identify H with torsion, and there is an integer M > 0 such that MH is topologically trivial. Then it is possible to have a set of M D9-branes whose gauge bundle actually has the structure group U(M)/ZM instead of U(M). The obstruction to lifting the U(M)/ZM bundle to a U(M) bundle is determined by H. In this case, the gauge bundle is called a twisted bundle. For any positive integer m, you can have N = mM D9-branes with the structure group of the bundle being U(mM)/ZM. In this case, the D-brane charge is classified by pairs (E, F) of the twisted bundles. The equivalence classes make a group KH(X).
In order to interpret KH(X) as the K-theory of representations of an algebra, you have to pick a particular twisted bundle W and consider a D-brane with boundary conditions determined by W. The W-W open strings transform in the adjoint representation, so the gauge parameters of the zero mode sector of the open strings are sections of W ⊗ [W bar]. Notice that although W is a twisted bundle, with structure group U(M)/ZM rather than U(M), W ⊗ [W bar] is an ordinary bundle, since the center acts trivially in the adjoint representation.
The sections of W ⊗ [W bar] form an algebra. If sji and tlk are sections of W ⊗ [W bar], where the upper indices are W-valued, and the lower indices are [W bar]-valued, then their product is
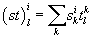
(st)li = [summation over k]skitlk
This is the algebra AW(X) of all endomorphisms or linear transformations of the bundle W. The algebra of open string field theory, for W-W open strings, reduces to AW if you look only at the zero modes of the strings. This is a good approximation t low energies where X is large compared to the string scale.
If H is zero, and W is a trivial rank one complex bundle, then AW(X) is just A(X). If H is zero, and W is a trivial rank N complex bundle, then including W means just that there are N x N Chan-Paton matrices everywhere. Therefore, in this case, AW(X) = A(X) ⊗ MN where MN is the algebra of N x N complex-valued matrices. In general, whatever H is, W is always trivial locally, so locally AW(X) is isomorphic to A(X) ⊗ MN.
A twisted bundle is equivalent to an AW-module, and the group KH(X) of pairs (E, F) of twisted bundles, modulo the usual equivalence, coincides with K(AW), the K-group of AW-modules. Therefore, KH(X), as defined in terms of pairs (E, F) of twisted bundles, is manifestly independent of W, while K(AW) appears to depend on W. Given any two distinct twisted bundles W and W’, the corresponding algebras AW and AW’, are distinct but are Morita equivalent, which implies that K(AW) = K(AW’).
So far, we have assumed that H is torsion. A typical example, important in AdS/CFT correspondence, is the spacetime X = AdS5 x RP5, where a torsion H-field on RP5 is used to describe Sp(n) rather than SO(2n) gauge theory in the boundary CFT. However, in most cases, H is not torsion. In that case, we must somehow take a large M limit of what we have just done. This was worked out by Bouknegt and Mathai, and independently by Atiyah and Segel. The suitable large M limit of U(M)/ZM is PU(H) = U(H)/U(1). In other words, for M = ∞, you replace ZM by U(1). This means that when H is not torsion, you can’t have a finite set of D9-branes and anti-D9-branes, but you can have an infinite set, with a suitable infinite rank twisted gauge bundle E or F. Then the D-brane charge is classified by the group KH of pairs (E, F) modulo the usual equivalence relations. Kuiper’s theorem, which in involves the contractability of U = U(H), plays an important role. The construction in the M = ∞ limit has the property that the noncommutative algebra whose K-group is KH is unique, independent of any arbitrary choice of twisted bundles W or W’. This depends on the number of D9-branes and anti-D9-branes being infinite.
Suppose spacetime is a product of cycles [curly W] ⊂ X9 where X9 is a 9-dimensional space, possibly noncompact. What are the possible cycles [curly W] ⊂ X9 which can be wrapped by a D-brane? The answer must meet the following two conditions.
1. The field theory on the D-brane must be consistent. For example, it must be anomaly free. This can put restrictions on the possible cycles on which free D-branes can wrap. Free D-branes are D-branes with no other branes ending on them.
2. We must identify branes which can be dynamically transformed into each other.
In the classification of D-brane charges in Type II string theory, the above conditions are met as follows.
1. A D-brane can wrap [curly W] ⊂ X9 only if
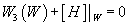
W3([curly W]) + [H] |[curly W] = 0
In H3([curly W], Z) where W3([curly W]) is the integral Stiefel-Whitney class of T[curly W]. Specifically, in de Rahm cohomology
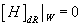
[H]DR|[curly W] = 0
A similar condition applies to other string theories. For instance, in the bosonic string, you have the same condition without the W3([curly W]) term.
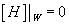
[H] |[curly W] = 0
2. Branes wrapping homologically nontrivial [curly W] can nevertheless be unstable if, for some [curly W]’ ⊂ X9
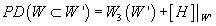
PD([curly W] ⊂ [curly W]’) = W3([curly W]’) + [H] |[curly W]’
Where the left hand side denotes the Poincare dual of [curly W] in [curly W]’. With the bosonic string, the issue of stability is complicated by the fact that the bosonic string includes tachyons, and is thus unstable for that reason. It is not always easy to disentangle the instability associated with the ordinary tachyon, which is always present in the bosonic string, from the instability of the brane, which is what we’re interested in.
First of all, free branes can wrap any homologically nontrivial cycle in X9. Second of all, a brane wrapping a nontrivial cycle is absolutely stable. Therefore, the homotopy classes of configurations of free branes can be labeled as
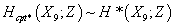
Hcpt*(X9; Z) ~ H*(X9; Z)
Imposing the above conditions is related to K-theory, and is closely related to a mathematical algorithm for computing K-theory called the Atiyah-Hirzebruch spectral sequence (AHSS), including the AHSS in the presence of non-torsion H-fields. The above two conditions are related to the computation of the AHSS at the third differential. Of course, the AHSS only gives an approximation of K-theory, since it is based on a filtration, and you gave to then solve an extension problem. Our improved understanding of the physical basis of the AHSS clarifies the physical basis for using the mathematical group KH*(X) for the classification of D-brane charges in the presence of a cohomologically nontrivial H-field. In Witten’s original paper, his argument only applied to the case where [H] was a torsion class. P. Bouwknegt and V. Mathai pointed out that the mathematical theory of KH*(X) makes perfectly good sense when H is nontorsion, and has a natural formulation in terms of C*-algebras.
The D-branes fall into superselection sectors which are labeled by their charges. The configurations which are referred to as instantons represent transitions between different sectors. Let’s say you have a transition from brane configuration Ai to a brane configuration Af. It is achieved by an interpolation A(t) with boundary conditions A(ti) = Ai and A(tf) = Af. The interpolation A(t) is an instanton. It is also a D-brane in space X9.
The discussion depends on the topology of X9 and the various branes, not on the geometry. If more information on the dynamics is given, then the D-branes A should be stationary in the equations of motion, and A(t) must satisfy the time dependent equations of motion where the parameter t is time. Then an important distinction should be made between two situations regarding the interpolation A(t).
1. When the transition between Ai and Af is a classically allowed transition, the interpolation A(t) should satisfy the equations of motion with Lorentzian signature.
2. When the transition between Ai and Af involves tunneling, and is not allowed classically, A(t) should satisfy the equations of motion with Euclidean signature.
Let’s look again at the first condition.
1. A D-brane can wrap [curly W] ⊂ X9 only if
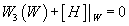
W3([curly W]) + [H] |[curly W] = 0
In H3([curly W], Z) where W3([curly W]) is the integral Stiefel-Whitney class of T[curly W]. In the de Rahm theory
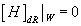
[H]DR |[curly W] = 0
In the de Rahm theory, it simply comes about since the H-field must be trivialized on the D-brane by the equations of motion
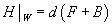
H|[curly W] = d(F + B)
At the level of integral cohomology, the above condition follows from the cancellation of global anomalies for fundamental open strings ending on the D-brane.
Here is the second condition.
2. Branes wrapping homologically nontrivial [curly W] can nevertheless be unstable if, for some [curly W]’ ⊂ X9
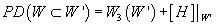
PD([curly W] ⊂ [curly W]’) = W3([curly W]’) + [H] |[curly W]’
Where the left hand side denotes the Poincare dual of [curly W] in [curly W]’.
To explain the second condition, let’s say you have a cycle [curly W]’ ⊂ X9 on which
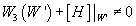
W3([curly W]’) + [H] |[curly W]’ ≠ 0
You can’t wrap a D-brane on [curly W]’, but let’s do it anyway with a D-brane instanton. We can then cancel the global anomalies on the D-brane worldvolume [curly W]’ by adding a magnetic source F on [curly W] ⊂ [curly W]’ such that
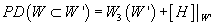
PD([curly W] ⊂ [curly W]’) = W3([curly W]’) + [H] |[curly W]’
A D-brane ending on [curly w] provides just such a magnetic source. Therefore, what you end up with is that a brane wrapping a spatial cycle [curly W] propagates in time, and then terminates on a D-instanton wrapping [curly W]’. This means the brane wrapping the spatial cycle [curly w] can be unstable and decays due to D-brane instantons wrapping [curly W]’.
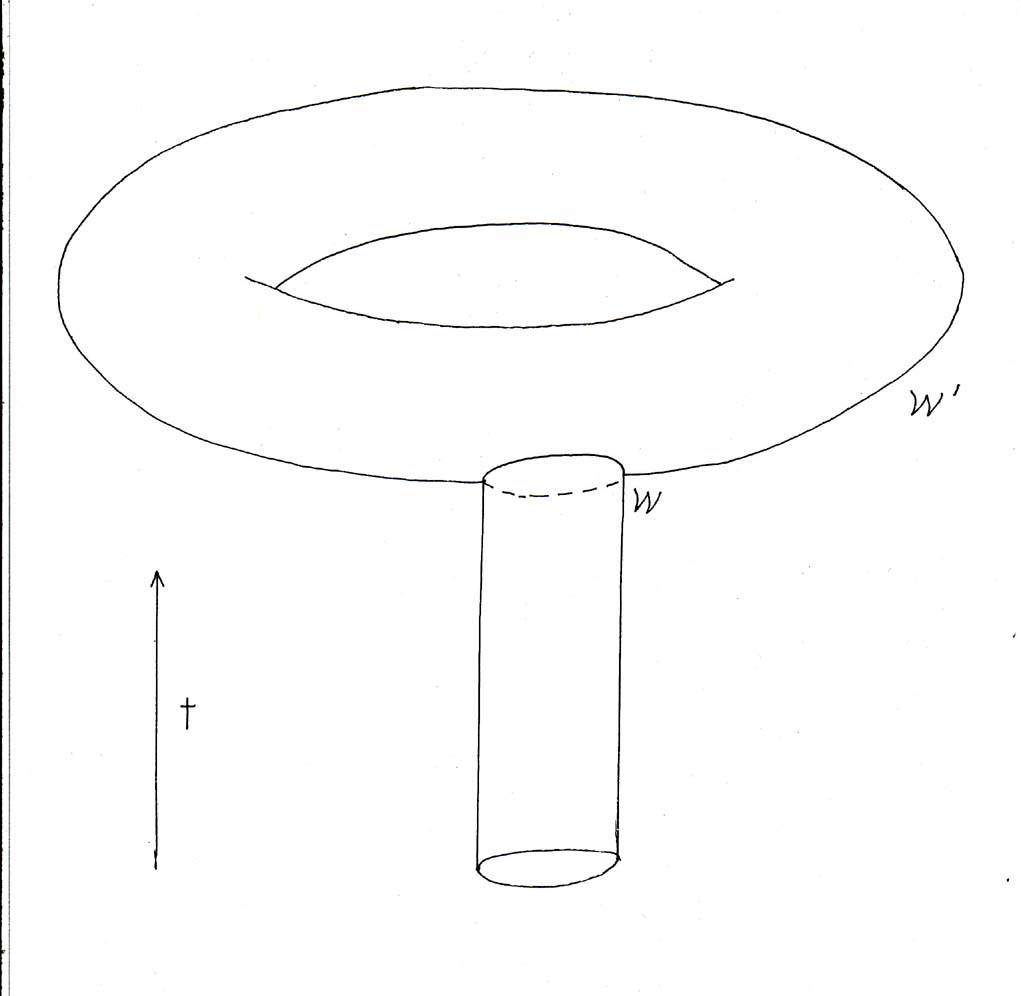
This only means that the brane wrapping [curly W] might decay. The brane wrapping [curly W] could be carrying other conserved charges that prevent decay to the vacuum. This is because we are only addressing the question of which cycles can be wrapped, and not addressing the full question of branes within branes, The second question can be answered by K-theory.
Now let’s show why the second condition does not really cancel the anomalies. In the de Rahm theory, this is easy since by the definition of a magnetic source
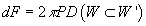
dF = 2πPD([curly W] ⊂ [curly W]’)
To extend the argument to the integral condition, you proceed as follows. For simplicity, we’ll put H = 0 but allow W3([curly W]’) to be nonzero.
Let’s say you have a D-instanton wrapping [curly W]’ where W3([curly W]’) is nonzero. Then let’s say another D-brane wraps [curly W] x Rt and ends on [curly W]’. In this situation, you can cancel the Freed-Witten anomaly if
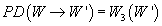
PD([curly W] → [curly W]’) = W3([curly W]’)
Remember that the Freed-Witten anomaly is based on the sign ambiguity in the definition of the path integral for worldsheet fermions. Therefore, you have a family of open string worldsheets St, 0 ≤ t ≤ 1, ending on [curly W]’ where S0 = S1.
The boundaries of these worldsheets ∂St sweep out a 2-cycle
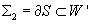
Σ2 = ∂S ⊂ [curly W]’
where S is the total space of the family. The holonomy of the fermion determinants around S1 is
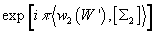
exp[iπ
Freed and Witten then extended the condition to require that this factor be unity for any 2-cycle. Σ2 ⊂ [curly W]’. We will assume for simplicity that the anomaly is due to a 2-cycle Σ2 with 2Σ2 = ∂D3 for some chain D3 ⊂ [curly W]’. You can learn about Σ2 by reviewing the definition of the mod-two Bockstein map relating w2 and W3. We begin by lifting w2 to an integral cochain [w bar]2 such that
<[w]2, C2> = <[w bar]2, C2> mod 2
for any 2-chain C2. Now
<[w bar]2, Σ2>
is an integer. If 2C2 = ∂D3 then
2<[w bar]2, C2> = <δ[w bar]2, D3> = 2
by the definition of the Bockstein, and since this is an equation of integers, you can divide by 2 to get
<[w bar]2, C2> =
Now let’s apply this to our cycle Σ2. Note that
exp[i ∫∂St A]
where St is the open string worldsheet. The extra factor cancels the ambiguity in the fermion determinant since
∫∂D3 (F/2π) = 1
so therefore
∫σ2 (F/2π) = ½
and therefore the magnetic source along [curly W] leads to a factor
exp[i ∫Σ2 F] = 1
canceling the ambiguous sign in the fermion determinant.
Let’s say you have DO-brane number in a spacetime with no torsion. The worldvolume of N D)’s defines a 0-cycle W0 which is Poincare dual to NX9 where X9 generates H9(X; Z) = Z, where X is connected and oriented. We identify N with the 0-brane number in the approximation
Hcptodd = k
However, if Σ3 is any 3-cycle in spacetime on which
∫Σ3 H = k
then you can consider a D2-instanton wrapping Σ3. This instanton will violate D0-charge since k worldlines of D0-branes must end on Σ3. The reason is because these end on monopoles, which are (2 + 1)-dimensional instantons for the U(1) field strengths of the D2-branew so if k worldlines of D0’s end on a D2-brane at positions xi ∈ Σ3, then
dF = 2π [summation of i from 1 to k] δ3 (x – xi)
In terms of cohomology, we are identifying
NX9 ~NX9 + H ∧ PD(Σ3)
And since
∫Σ3 H = k
we know that
H ∧ PD(Σ3) = kx9