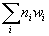
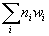
[summation over i] niwi
where wi form a basis if H2(X, Z) has a Poincare dual 7-form ω7 = niω7i. D4-instantons wrapping
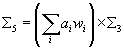
Σ5 = ([summation over i]aiwi) x Σ3
lead to the identification ni ~ni + kai. A d4-instanton wrapping a 5-manifld Σ5 violates the rule [H] = 0. To account for the trivialization dF = dF + H, you must have D2-brane worldvolumes ending on the homology class k(Σ aiwi) in Σ5.
As an example with torsion in Hcpt*(X, Z), let’s say you have a simple example with H = 0. Let’s say c = Sq3(c0) for some c0 ∈ H3(X, Z). Then c is Sq3 closed, and thus corresponds to some K-theory class. Therefore, it is also Sq3 exact, and its K-theory lift is zero. Since its K-theory charges vanishes, you would expect a brane with PD(c) = [curly W] to decay. Physically, PD(c) = Q3 is the homology class of a cycle which is wrapped by a D5-brane instanton. Since Sq3(c0) is nonzero, Q6is not spinc.
You can cancel the global anomalies by allowing the worldvolume Q3 of the D3-brane to end on Q6 provided
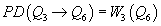
PD(Q3 → Q6) = W3(Q6)
Next, I’m going to discuss the Atiyah-Hirzebruch spectral sequence or AHSS. A K-theory class X in K*(X) determines a system of integral cohomology classes. If X ∈ K0(X), these are Chern classes ci(X) ∈ H2i(X, Z). If X ∈ K1(X), there are classes ω2i + 1 ∈ H2i + 1(X, Z) related to Chern-Simons invariants. However, if you have such a system of cohomology classes, it did not in general come from a K-theory class. The AHSS is a successive approximation scheme for computing the necessary relations on the classes. In each step of the process, you take the results from the last approximation to do the next approximation. In the first approximation
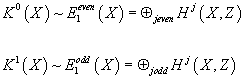
K0(X) ~ E1even(X) = ⊕j even Hj(X, Z)
K1(X) ~ E1odd(X) = ⊕j odd Hj(X, Z)
Using the differential, d3 : Hj(X, Z) → Hj + 3(X; Z) where (d3)2 = 0, you compute
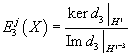
E3j(X) = (ker d3 |Hj)/ (Im d3 |Hj + 3)
and set

E3even = ⊕j even E3j(X)
to obtain the first correction
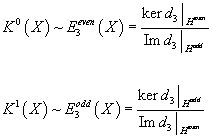
K0(X) ~E3even(X) = (ker d3 |Heven)/(Im d3 |Hodd)
K1(X) ~H3odd(X) = (ker d3 |Hodd)/(Im d3 |Heven)
Then, using the differential d5 : E3j(X, Z) → E3j + 5(X; Z) you compute
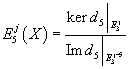
E5j(X) = (ker d5 |E3j)/(Im d5 |E3j – 5)
to get the next approximation, and then you just continue the process. You keep computing cohomology in this way to get E∞j(X). The procedure is guaranteed to stop after a finite number of steps as long as X is finite dimensional. Then the associated group Gr(X) is defined by
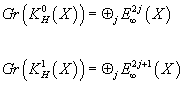
Gr(KH0(X)) = ⊕j E∞2j(X)
GR(KH1(X)) = ⊕j2j + 1(X)
In good cases, you can identify Gr(K) = K. The AHSS is useful because it’s a clearly defined algorithm.
One problem is that you obviously need to have expressions for the differentials, d3, d5, etc. The initial term of the spectral sequence is C*(X, h*(pt)), for any generalized cohomology theory h*. A simple expression for the differential d3 is known. In ordinary K-theory, Atiyah and Hirzebruch identified it as the third Steenrod square, d3 = Sq3. For twisted K-theory, d3 = Sq3 + H, in the context of C*-algebra. In de Rahm theory, you get the simple expression
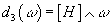
D3(ω) = [H] ∧ ω
In general, not much is known about the higher differentials. There are scattered results for H = 0, and it appears that nothing is further is known for H nonzero. Fortunately, on compact spin 10-folds at H = 0, you don’t need the higher differentials.
Another problem is that the AHSS is only an approximation to KH*(X). Let’s say you have a cell decomposition or simplicial decomposition, X0 ⊂ X1 ⊂ X2 .....⊂ Xn. Then we define Kp*(X) to be the classes which become trivial upon restriction to Xp. Obviously, KP + 1* ⊂ Kp*(X). The AHSS really computes the associated graded space, which is
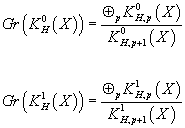
Gr(Kh0(X)) = (⊕p KH, p0(X))/(KH, p + 10(X))
Gr(KH1(X)) = (⊕p KH, p1(X))/(KH, P + 11(X))
When you go from that to the full K-theory group, you need to solve an extension problem to get the correct torsion group. Fortunately, in many cases, there is either no extension problem, or it’s not severe. However, there are important examples, such as the compact Lie groups of rank greater than two, and homogeneous spaces, where this complication can be significant. Also, the extension problem is important for orbifolds.
Remember, we are working on spacetimes of the form R x X9. Let’s say you have a brane wrapping a p-manifold [curly W] ⊂ X9. You can associate to [curly W] several topological classes. First of all, [curly W] has an associated homology cycle
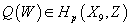
Q([curly W]) ∈ Hp(X9, Z)
Since X9 is oriented, there is a Poincare dual integral cohomology class
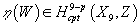
η([curly W]) ∈ Hcpt9 – p(X9, Z)
Furthermore, the brane wrapping [curly W] has gauge fields and consequently the D-brane charge is really associated with a class in the K-theory of X9. The homology class Q can be extracted from the K-theory class, since Q represents the support of the K-theory class.
If the D-brane is realized by tachyon condensation, the support is the locus where the tachyon field vanishes. You then get a cohomology class from η = PD(Q). More generally, to a collection (ω1, ω2,...ω9), we associate a collection of branes by taking Poincare duals to obtain a collection of spatial cycles (PD(ω1), PD(ω2),...PD(ω9)) around which D8, D6,...D0-branes are wrapped. A necessary condition for a cohomology class
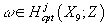
ω ∈ Hcptj(X9; Z)
to survive E∞j is that

d3(ω) = (Sq3 + [H])ω = 0
This is replaced by the anomaly cancellation condition. We therefore interpret d3(ω) = 0 as a partial requirement for global anomaly cancellation. In fact, it is a weaker condition than
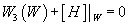
W3([curly W]) + [H]|[curly W] = 0
It was once believed that in the absence of D-branes, Ramond-Ramond field strengths were classified by twisted K-theory. Evidence for this conjecture came from an analysis of symmetric boundary conditions in the worldvolume theories of open strings, from the analysis of the Chan-Paton bundles on various unstable D-branes, and from the conditions imposed on D-brane embedding by global worldsheet anomaly cancellation. However, within a few years, Diaconescu, Moore, and Witten realized that, in Type IIB superstring theory, the twisted K-theory classification of fluxes is inconsistent with S-duality. This shouldn’t have been surprising since none of the evidence for this conjecture that I listed above is covariant with respect to S-duality. For example, searching for D-branes as boundary conditions in the conformal field theories will not yield an S-duality covariant classification of branes unless you also include Neveu-Schwarz branes, and examine the boundary conditions of (p, q)-strings, which would be difficult as the fundamental string coupling diverges near an NS5-brane. Witten’s construction of untwisted K-theory from tachyon condensation of stacks of D9 and anti-D9-branes also could not be S-dualized as D9-branes are already poorly understood, and their S-duals are unknown if they exist at all. Freed and Witten’s worldsheet anomaly was easily S-duality covariantized. However, except in the case of 3-form field strengths, it was not known how to use it to find a consistency condition for field strengths.
One possible solution to this problem is to use the BRST formalism. You can identify a set of large Ramond-Ramond gauge transformations using the Type II supergravity action, which are essentially those which keep the Wilson loops invariant. These symmetries act on the integral lattice of de Rahm cohomology which satisfies the Dirac quantization condition. This lattice is often smaller than the full integral cohomology, in which the various field strengths are believed to be valued. You use the Freed-Witten anomaly to extend the gauge transformations to the full integral cohomology. The BRST cohomology of the RR gauge transformations is isomorphic, as a set, to twisted K-theory. Atiyah and Hirzebruch showed that K-theory may be constructed from integral cohomology by taking its cohomology with respect to a series of differential operators. In other words, a quotient of a subset of cohomology approximates K-theory, and if you take a quotient of a subset of that, you get a better approximation. Jarah Evslin showed that Atiyah and Hirzebruch’s differential operators are the same as BRST charges corresponding to the large RR gauge transformations. In addition, the extra wrong degree cohomology classes that you add to the sequence are the ghosts and antighosts. This is an unusual application of the BRST formalism because the gauge symmetry is discrete, so the ghosts and antighosts don’t have propagating degrees of freedom. This all suggests that to find the S-duality covariant classification of RR and NSNS field strengths in Type IIB, and also the correct classification in Type IIA, you need to take the BRST cohomology, not only with respect to the RR gauge transformations, but also with respect to the NSNS gauge transformations. However, the NS 3-form field strength is itself used in the RR gauge transformations, and therefore these two symmetries can’t be disentangled. The result is that the collection of NSNS and RR field strengths together don’t form a cohomology or even an additive group. This shouldn’t come as a surprise since the field strengths are solutions to supergravity equations of motion which are nonlinear. When you quotient by the NSNS transformations, you lose more than just the addition. The S-duality covariant classification usually has a different cardinality than the twisted K-theory, as was shown in the case of Klebanov-Strassler geometry.
Edward Witten has speculated that there may be a twisted K-theory based formulation of Type II string theories. However, efforts at constructing such a formulation have been complicated by the fact that twisted K-theory classes are not easily expressed as fields, and so are not easily treated using the standard tools of quantum field theories. However, using the BRST construction, you only need to start with fields that are ordinary differential forms, supplemented with the Dirac quantization conditions, and the various ghost towers that construct a Deligne cohomology and the description of the torsion classes. That is, the field content is the same as the p-form gauge theory. Then you find the symmetries of the path integral, include the ghosts, and calculate the BRST cohomology.
This gives a BRST cohomology which is larger than twisted K-theory. In order to get twisted K-theory you have to ignore the values of the various Wilson lines, which are exponentials of the integrals of the gauge connections. You could also not ignore them, in which such case, you get a differential version of twisted K-theory. The description of the twisted K-theory of spacetime M as a BRST cohomology is summarized as follows, using Type IIA as an example.
| BRST | K-theory | Type IIA Supergravity | Type IIA String Theory |
| fields | ⊕kH2k(M) | RR diff. Forms G2k | RR integral classes G2k |
| ghosts | ⊕kH2k + 1(M) | gauge x forms/branes | gauge xforms/branes |
| BRST operator | d2p + 1 | d3 = H∧ | =d3 = Sq3 + HU, d5 |
| gauge x forms | d : Hodd → Heven | Wilson loops | FW monodromy |
| constraints | d : Heven → Hodd | Bianchi identities | source FW anomaly |
| physical fields | KH0(M) | orbits of Bianchi identities | orbits of FW solutions |
| anomalies | KH1(M) | stable p-branes | stable D-branes |
Stable consistent D-branes correspond to anomalies, despite the fact that their partition functions are gauge invariant. In fact, they appear in the supergravity equations of motion as violations of the conservation of RR current. They also correspond to anomalies as instantonic D-branes which form, sweep out nontrivial cycles, and then decay, changing the cohomology class of fluxes that they source, and therefore mediate a tunneling between different source-free RR solutions.
Notice that on their worldvolumes, the unimproved field strengths are not defined, similar to the worldvolume of a magnetic monopole in QED where the gauge potential A is not defined. In the quantum theory, this may correspond to a nontrivial inner product between states with stable D-branes and states with Ramond-Ramond fields that are pure gauge. The fact that D-branes correspond to elements of the BRST cohomology, and specifically are BRST closed, implies a sort of Wess-Zumino consistency condition, which is enforced classically by the supergravity equations of motion, and quantum mechanically by the Freed-Witten (FW) anomaly.
The field content of eleven-dimensional supergravity is (g, C3, ψ1), where g is the metric tensor, C3 is the antisymmetric tensor field, usually called the C-field, and ψ1 is the Rarita-Schwinger field, which is a fermion field with spin 3/2. The Lagrangian of the supergravity theory is simple compared to other higher dimensional supergravity theories. It is made of kinetic terms for the three fields involved, and in addition, contains an important piece dictated by supersymmetry, the Chern-Simons term, which is a topological term independent of the metric. If you include quantum effects of anomalies, then you also add a one-loop term made of C3 and some eight-dimensional polynomial in the Pontryagin class of the tangent bundle of the eleven manifold Y11.
Varying the action of 11d supergravity with respect to each of its fields leads to a set of three equations of motion, which are the Einstein equation for g, the Maxwell-like equation for C3, and the Rarita-Schwinger equation for ψ. It’s very difficult to solve these differential equations so you only do it in particular cases. Among the interesting solutions are the membrane M2 and the fivebrane M5. These are characterized by being BPS. This means that they are stable against perturbations, and thus do not receive quantum corrections. This implies that such solutions can be trusted in the quantum theory, meaning at strong coupling.
M-theory is a quantum theory in eleven dimensions whose weak coupling limit is classical eleven-dimensional supergravity. There is no intrinsic formulation of the theory without using its limits. There are proposals for such definitions, such as the matrix model, but they have their limitations, especially as far as topology. M-theory also connects the various string theories through a web of dualities, such as perturbative target space T-duality, and nonperturbative strong-weak coupling S-duality. So you can try to study M-theory from its low energy limit which is eleven-dimensional supergravity, or from its connection to the duality web. In the first approach, you use the BPS solutions as objects in M-theory itself.
The degree three field C3 is responsible for the nontrivial topology of M-theory. In analogy to electromagnetism, where the one-form potential couples to the worldline of the electron, and its dual couples to the worldline of the monopole, you have an analogous situation here where C3, viewed as an electric potential, couples to the worldvolume of the M2-brane, and the dual potential C6, viewed as a magnetic potential, couples to the worldvolume of the M5-brane. This is due to the eleven-dimensional Hodge duality between G4 = dC3 and *G4 = dC6 + ... and follows directly from the equations of motion for C3. In supergravity, the non-gravitational fields are usually taken to be differential forms. However, when you take anomalies into account, such fields are expected to form classes in integral cohomology. However, the situation is usually more subtle. For the case of G4, you get a shifted quantization condition
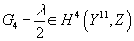
G4 - (λ/2) ∈ H4(Y11, Z)
Where λ is half the Pontryagin class of TY11.
Motivated by the E8 x E8 heterotic string theory on the boundary of Y11, Edward Witten showed that G4 can be interpreted as the class of an E8 bundle in the eleven dimensions. In 2003, Jarah Evslin and Hisham Sati analyzed the question of supersymmetry in such a theory, and gave an approximate construction of the 11d gravitino as a condensate of the gauge theory fields.
The Kaluza-Klein dimensional reduction of eleven-dimensional supergravity leads to Type IIA supergravity theory whose bosonic field content includes the Ramond-Ramond (RR) fields F2p (p = 1, 2, ...5), and the Neveu-Schwarz (NSNS) field H3. V. Mathai and Hisham Sati performed the dimensional reduction. In Type II string theories on X10, you have refinements of the cohomology description, except in this case, you are led to K-theory, K0(X10) for Type IIA, and K1(X10) for Type IIB. In the presence of H3, the corresponding K-theories are twisted. The reduction of E8 to ten dimensions leads to an LE8 bundle. This was first proposed by A. Adams and Hisham Sati, where H3 serves as an obstruction to lifting the loop group bundle to its central extension. This bundle picture can be considered complementary to the twisted K-theory view. Adding a cosmological constant F0 leads necessarily to an H3 which is trivial in cohomology, meaning H3 = dB2. Instead of looking at the fields, you can look at it from the point of view of D-branes. These are used in homology, and you can go back and forth between cohomology and homology using Poincare duality. There is an analogy with electromagnetism where the branes act as sources of charges that appear as delta-function violations of the corresponding Bianchi identities. This can be viewed as a higher degree analog of Dirac charge quantization for monopoles. The Antiyah-Hirzebruch spectral sequence (AHSS) serves as a tool to detect the difference between cohomology and K-theory, and is thus a powerful tool for D-brane realization. Jarah Evslin proposed a modification of the AHSS in order to describe the group of conserved RR and NSNS charges.
The correspondence between M-theory and Type IIA string theory holds at the quantum level in the path integral formulation, meaning at the level of partition functions. The former is governed by E8 gauge theory, and the latter by K-theory. The corresponding match for twisted K-theory was started by V. Mathai and H. Sati, where a nontrivial M-theory circle bundle is considered, the NSNS field H3 nontrivial in cohomology is added, and the corresponding vector bundles are taken not to be lifted from the base. The construction of the K-theory torus is done as in the untwisted case. You also see the appearance of eta differential forms, which are higher degree generalizations of the eta invariant.
The partition function in Diaconescu, Moore, and Witten’s theory has an anomaly given by the seventh integral Stiefel-Whitney class W7. In 2004, Igor Kriz and Hisham Sati showed that the vanishing of this anomaly is equivalent to orientability of spacetime with respect to complex elliptic cohomology E. Motivated by this, an ellitpic cohomology correction to the Type IIA partition function was defined. The generators of E were proposed as corresponding to M2 and M5-branes in the M-theory limit. Other aspects of string theory also point to elliptic cohomology. In the presence of background NSNS flux, the description of the RR fields in Type IIB string theory using twisted K-theory is not compatible with S-duality. In 2005, Igor Kriz and Hisham Sati showed that other possible variants of twisted K-theory would still not resolve this issue, and proposed a possible resolution using elliptic cohomology. Another piece of evidence for elliptic cohomology is modularity in Type IIB, where there is an elliptic curve that lifts the theory to twelve-dimensional F-theory. Kriz and Sati interpreted this elliptic curve in terms of elliptic cohomology.
The above elliptic cohomology description in Type II string theory can, at least mathematically, be continued to M-theory via a Kunneth formula for E. You can then ask whether E will ultimately be the theory describing the fields of M-theory. Related to this is trying to understand the nature of G4. For this purpose, in 2005, Hisham Sati wrote the Chern-Simons terms and the one-loop terms n the M-theory action in terms of new characters involving the M-theory four-form and the string classes. The latter are defined as analogs to the usual string class of rank four, λi = pi/2. This suggests the existence of a theory of higher characteristic classes, where the Chern classes and Chern characters are replaced by those new classes and characters. This formalism can be used to give a unified expression for the class of G4 and its dual, called the Θ class, in analogy with the K-theoretic quantization of the RR fields.
Diaconecsu, Moore, and Witten have shown that the topological part of the M-theory partition function is an invariant of an E8 gauge bundle over the 11-dimensional bulk. Normally, an 11d gauge theory can’t exhibit linearly realized supersymmetry, but here the gauge theory is nonsupersymmetric and flows to 11d supergravity only in the infrared, with supersymmetry arising as a low energy accidental degeneracy.
In 1996, Horova and Witten demonstrated that when M-theory is compactified on a manifold with boundary, the anomalies caused by chiral gauginos and gravitinos on each boundary component precisely cancel the anomalies that flow in from the bulk. This cancellation occurs only if each boundary component supports precisely 248 10-dimensional vector multiplets,. All transforming in the adjoint representation of E8. Furthermore, the topological contribution to the M-theory partition function is in fact an invariant of the Dirac operator of a mysterious 11-dimensional E8 gauge theory. While the nature of the gage theory is unknown, the anomaly cancellation of Horova and Witten, as well as the 10-dimensional N = 1 supersymmetry on every boundary component, place strong constraints on its construction. For simplicity, we restrict ourselves to the case of flat, topologically nontrivial 11-dimensional space, and also neglect higher order Fermi field contributions.
E8 gauge invariance combined with local supersymmetry invariance requires the relation
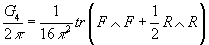
G4/2π = (1/16π2) tr (F ∧ F + (1/2)R ∧ R)
Between the 11d 4-form field strength G4 and the 10D N = 1 supersymmetry vector multiplets field strength F on every 10-dimensioanl boundary component. Let’s say you have an E8 gauge bundle such that the above equation holds everywhere in the 11-dimensional bulk. The fact that such a bundle exists is a consequence of M-theory’s shifted flux quantization condition. The uniqueness of this bundle results from the uniquely simple low dimensional topology of the E8 group manifold.
In addition to the 248 gauge bosons, you also need 248 Majorana gauginos propagating in the 11d bulk, as well as the 11d graviton. Using the above equation, you can construct the 11d supergravity 4-form G4 from the vectors. Ten dimensional N = 1 supersymmetry covariance allows you to find the analogous construction of a chiral half of the 11-dimensional gravitino. Eleven-dimensional Lorentz invariance allows you to construct the other half. Therefore, each gauge theory configuration is identified with a single supergravity configuration, meaning that the construction can’t be covariant under 11d supersymmetry since the gauge fields are not part of any representation of 11d supersymmetry.
Therefore, you should identify each gauge field configuration with not only the single supergravity configuration given earlier, but with all of the supergravity configurations which are related to that configuration by an 11d supersymmetry transformation. Therefore, supergravity field configurations related by supersymmetry transformations will be identified with the same gauge field configuration, and thus the same physical state. Physically equivalent configurations on the gauge theory side are also equivalent on the supergravity side, and the E8 gauge transformations are realized as abelian gauge transformations of the M-theory 3-form.
The low energy effective description of M-theory is 11-dimensional supergravity. The fields of this theory live in a single supermultiplet which contains the gravition, the gravitino ψ, and a three-form C3, whose exterior derivative, times 6, is the four-form field strength G4. If the dynamics of M-theory are to be formulated in terms of an E8 gauge theory, it would be great to have relations between the fields of the 11d supermultiplet, and the fields of the gauge theory, which are the 1-form connection A with field strength F, and an adjoint Majorana gaugino χ. Horova and Witten showed that gauge and gravitational anomaly cancellation on any 10-dimensional boundary of M-theory enforces the relation
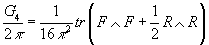
G4/2π = (1/16π2) tr (F ∧ F + (1/2)R ∧ R)
On the boundary, where R is the curvature 2-form of the tangent bundle.
Witten used locality to argue that such relations, at the level of cohomology, can be extended to the bulk, although it does not follow from this argument that there is an E8 gauge field strength in the bulk. One reason why there is an E8 gauge field strength in the bulk is that the low energy effective action for M-theory on the 11-fold Y11 contains the topological terms
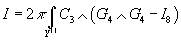
I = 2π [integral over Y11] C3 ∧ (G4 ∧ G4 - I8)
Where I8 is a quartic in the curvature tensor. This can be related to a sum of indices of an E8 gauge theory on an auxiliary 12-dimensional manifold. The ambiguity in I is the integral of its exterior derivative over a closed 12-manifold. The integral may be nonvanishing because C3 is not necessarily globally defined. The path integral is well-defined if this integral, added to a contribution from the square root of the determinant of the Rarita-Schwinger operator is an integer.