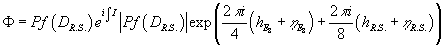
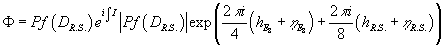
Diaconescu, Moore, and Witten used a theorem of Atiyah, Patodi, and Singer to evaluate the contribution of this topological term and the Pfaffian determinant of the Rarita-Schwinger operator to the phase of the path integral measure.

Φ = Pf(D_RS) e^i∫I = | Pf(D_RS)| exp ((2πi/4) (h_E₈ + η_E₈) + (2πi/8) (h_RS + η_RS))

where η is the η-invariant of the corresponding operator, which is either the E₈ gauge theory Dirac operator or the Rarita-Schwinger operator, and h is its number of zero modes. So therefore, h_E₈ would be the number of zero modes of the E₈ gauge theory operator, η_RS would be the invariant of the Rarita-Schwinger operator, etc. Therefore, a part of the path integral measure of 11-dimensional supergravity can be expressed in terms of the bulk E₈ gauge theory. Also, the partition function consists of a sum over E₈ gauge theory configurations.

At the beginning of my paper “Beyond the Standard Model”, I discuss the different Lie groups, which are defined as the groups of rotations within different types of space. For instance, SO(n) is often described as the group of rotations within real space, although actually it’s the group of rotations within projective real space.

1. So(n) is the group of rotations within real projective space RPⁿ.

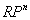
2. SU(n) is the group of rotations within complex projective space CPⁿ.

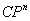
3. Sp(n) is the group of rotations within quaternionic projective space HPⁿ.

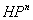
4. E₆ is the group of rotations within the projective plane over the bioctonions, (C ⊗ O)P².

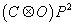
5. E₇ is the group of rotations within the projective plane over the quateroctonions (H ⊗ O)P².

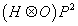
6. E₈ is the group of rotations within the projective plane over the octooctonions, (O ⊗ O)P².

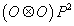
7. F₄ is the group of rotations within the projective plane over the octonions, OP².

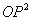
8. G₂ is the automorphism group of the octonions.

With 248 dimensions, E₈ is the biggest of the exceptional Lie groups, and also the least understood. The easiest way to understand a group is to realize it as the symmetries of a structure you already understand. Of all the simple Lie groups, E₈ is the only one whose smallest nontrivial representation is the adjoint representation. This means that in the context of linear algebra, E₈, is most simply described as the group of symmetries of its own Lie algebra, which is circular reasoning. You can also describe E₈ as the isometry group of a 128-dimensional Riemannian manifold called (O &0times; O)P². However, this manifold is usually defined in terms of E₈ so we’re again stuck with circular reasoning. Nobody knows how to rigorously define (O ⊗ O)P² without first defining E₈. Therefore, E₈ remains enigmatic.

Fortunately, it became slightly less enigmatic recently. Even though the E₈ exceptional Lie algebra was discovered by Wilhelm Killing in 1887, and it was constructed by Eli Cartan in 1894, it was not until 2007 that a team of 18 mathematicians, led by Jeffrey Adams, after four years of hard work and 77 hours on a supercomputer, finally calculated all the representations of E₈. The coefficients of the character formulas for infinite dimensional irreducible representations of E₈ depend on some large square matrices consisting of polynomials called the Lusztig–Vogan polynomials. It was these matrices that the group calculated. The calculation was 60 gigabytes. If you were to try to actually write down the solution, you would need a piece of paper larger than New York City!

Starting from e₈, you can define E₈ to be the simply-connected Lie group with this Lie algebra. The subgroup of E₈ generated by the Lie subalgebra so(16) ⊂ e₈ is Spin(16)/Z₂. This let’s us define the octooctonic plane by

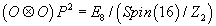
(O ⊗ O)P² = E₈/(Spin(16)/Z₂)

The tangent space at any point of this manifold is isomorphic to S₁₆⁺ ~ (O ⊗ O)P². This partially justifies calling it “octooctonic projective plane”, although it does not satisfy the usual axioms for a projective plane. You can put an E₈-invariant Riemannian metric on the octooctonic projective plane by the technique of averaging over the group action. It turns out that

E₈ ~Isom((O ⊗ O)P²)

So here you have a group defined as the isometry group of a given manifold. However, every group is itself associated with a different manifold which has the holonomy of that group. Therefore, the E₈ group is associated with a manifold called the group manifold E₈. So you have a manifold which is used to define a group which is used to define a different manifold. I’ll give another example of the same thing. Here are some of the holonomy groups of RP³ are

π₁(RP³) = Z₂

π₂(RP³) = 0

π₃ (RP³) = Z

π₄(RP³) = Z₂

The isometry group of RP³ is SO(3), which is associated with the SO(3) manifold. Some of its homotopy groups are

π₁(SO(3)) = Z₂

π₂(SO(3)) = 0

π₃(SO(3)) = Z

π₃(SO(3)) = Z₂

So you have a manifold, say RP³, associated with groups in one way, which are the homotopy groups, say π₁(RP³), and associated with a different group in another way, which is the group of rotations, SO(3), and that group is then associated with its own homotopy groups, such as π₁(SO(3)).

The low dimensional topology of E₈ is in one way, the simplest among nonabelian Lie groups. E₈ has only one nontrivial homotopy group of dimension less than 16, which is π₃(E₈) = Z. This means that on a manifold of dimension less than 16, E₈ bundles are topologically characterized by a single characteristic class, which is the first Pontryagin class.

p₁ = (Tr(F ∧ F))/8π²

The only restriction on this class is that its integral over any 4-cycle be an even integer. All other semisimple Lie groups have additional nontrivial low dimensional homotopy groups, and therefore their principle bundles can not be characterized by a single characteristic class. This agrees with what we know about M-theory which at low energies is also described by a 4-form. The 4-form flux of M-theory is a combination of this characteristic class and the first Pontryagin class of the tangent bundle.

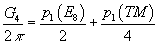
G₄/2π = p₁(E₈)/2 + p₁(TM)/4

Notice that the shifted flux quantization condition of G₄ is automatic in this construction. The first term on the right hand side is an integral cohomology class, while the second term could be an integral cohomology class or could be half an integral cohomology class. Therefore, the failure of the left hand side to be integral is precisely equal to the failure of the second term of the right hand side, or the mod 2 part of p₁(TM)/2.

As a result of the fact than an E₈ bundle is described by a single closed form, an E₈ bundle on a manifold of dimension less than 16, has only one type of topological defect, which is the M5-brane. Of course, if it has M5-branes, then it automatically also has M2-branes. For instance, an M2-brane is created when two M5-branes cross via the Hanany-Witten mechanism. The M5-brane is a codimension 5 defect where the form fails to be closed.

Before I describe the E₈ gauge theory model of M-theory, let’s first describe a simpler case of the ‘t Hooft-Polykov monopole, in order to gain insight into the role of the M5-brane defect. Let’s say you have an SU(2) gauge theory in at least three dimensions with a scalar Φ^a that transforms in the adjoint of SU(2), and is

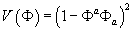
V(Φ) = (1 - Φ^aΦ_a)²

The group SU(2), like E₈, is a simple Lie group, and so π₃(SU(2)) = Z. Therefore, the gauge bundle admits a codimension 5 defect constructed same as the M5-brane is constructed. However, because a configuration of Φ is a map from spacetime to SU(2), the presence of an adjoint Higgs field in this model allows a defect of codimension 3. If you impose a finite energy condition on 3-dimensional slices of spacetime, then on each of these slices, Φ is a map from S³ times an irrelevant space to SU(2) ~ S³. Such a map is classified up to homotopy by an element n ∈ π₃(SU(2)) = Z, where n is the ‘t Hooft-Polykov magnetic monopole charge of the 3-dimesional slice.

The field strength F of a U(1) gauge theory can be constructed from the field strength G^a of the original SU(2) and the scalar field via

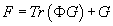
F = Tr (ΦG) + G

In the U(1) gauge theory description, the ‘t Hooft-Polykov monopole appears to be a Dirac monopole in the following sense

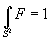
[integral over S²] F = 1

for any 2-sphere that links the monopole once. However, at microscopic distances, this abelian effective description breaks down, and the physics, like asymptotic freedom, can’t be understood without the nonabelian description.

This construction could be repeated with an E₈ gauge theory that had a scalar Higgs transforming in the adjoint of E₈. In this case, the configuration of the Higgs field in a 3-plane transverse to the monopole, after a 1-point compactification of this 3-plane, will again be an element n ∈ π₃(E₈) = Z, where n is the monopole charge.

The existence of the adjoint scalar was crucial to the construction of the ‘t Hooft-Polykov monopole. Such a scalar does not exist in the E₈ gauge theory model of M-theory, so you don’t have a ‘t Hooft-Polykov monopole or an abelian two-form field strength. In trying to construct an E₈ scalar from the E₈ field strength, notice that although there is no adjoint scalar with which to contract its E₈ indices, there is the E₈ field strength itself. Specifically, you can construct an abelian four-form [G tilde]₄ from the E₈ field strength via

[G tilde]₄ = (1/8π) tr(F ∧ F)

so that F plays the same role as the Higgs field in the example of the monopole. As in the case of the ‘t Hooft-Polykov monopole, this description breaks down at the topological defect, where the nontriviality of π₃(E₈), and thus the nonabelian nature of the original high energy theory becomes impossible to ignore.

Type II string theories in ten dimensions contain, in addition to gravity and fermions, p-form fields, which are the Ramond-Ramond (RR) and Neveu-Schwarz (NS) fields. D-branes are charged under these p-forms. It is by now well known that RR charges in the absence of NS fields can be classified by K-theory of spacetime, specifically K⁰(x) for Type IIB, and K¹(x) for Type IIA. The RR fields are also classified by K-theory with the roles of K⁰(X) and K¹(X) reversed. In the presence of a NS B-field, or its field strength H₃, the fields and the charges are classified by twisted K-theory. It was shown by Freed and Witten by analysis of worldsheet anomalies for the NS field, [H₃] ∈ H³(X, Z) is a torsion class. M-theory is a theory in eleven dimensions which is not yet known except in specific regions or points in its moduli space. Witten showed that the topological part can be encoded in the index theory of an E₈ gauge bundle. At the level of supergravity, the low energy limit of string theories and M-theory, there is an explicit relation between the two given by the Kaluza-Klein relation. Actually, it’s much more subtle at the quantum level due to the existence of nontrivial phase factors in the partition function. E. Diaconescu, G. Moore, and E. Witten showed that you can also relate the corresponding partition functions, specifically the one derived using E₈ gauge theory in eleven dimensions, and the one derived from K-theory in ten dimensions. They restricted themselves mostly to the RR sector. This has been generalized to include the fermions, one-loop contributions, and membrane instantons, as well as including flat background NS potentials. The partition functions are T-duality invariant only after including these effects.

Let’s say Y is an eleven-dimensional spin manifold corresponding to M-theory, and X is a ten-dimensional manifold which is the base space of a circle bundle with total space Y, and corresponds to Type IIA string theory. Z is a twelve-dimensional manifold which is a disk bundle over X, whose boundary is a circle bundle Y over X. The basic set up for the bundles is

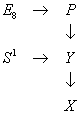
where P is a principle E₈ bundle over the 11-dimensional manifold Y, which is in turn is a principle S¹ bundle over the 10-dimensional manifold X. Then Y has a supergravity field whose field strength is a closed 4-form G₄, that is related to the integral characteristic class invariant a of P by

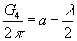
G₄/2π = a - λ/2

Where λ/2 is equal to half the first Pontryagin class p₁(Y) of Y.

We are interested in the comparison using the metric

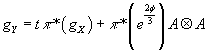
g_Y = tπ*(g_X) + π*(e^2φ/3)A ⊗ A

in the large volume limit as t → ∞.

M-theory has three kinds of impurities which are membranes, five-branes, and boundaries. The low energy theory is eleven-dimensional supergravity. The massless degrees of freedom are the metric g, a three-form potential C₃, and a Rarita-Schwinger fermionic spin 3/2 field ψ_M. The action of eleven-dimensional supergravity is

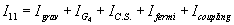
I₁₁ = I_grav + I_G₄ + I_{C. S.} + I_fermi + I_coupling

where

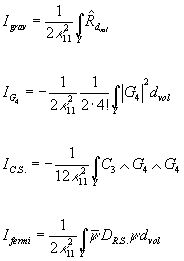
I_grav = 1/ 2κ₁₁² ∫_Y [R hat]d_vol

I_G₄ = -1/ 2κ₁₁² (1/2 . 41)∫_Y |G₄|² d_vol

I_{C. S.} = 1/1 2κ₁₁² ∫_Y C₃ ∧ G₄ ∧ G₄

I_fermi = 1/ 2κ₁₁² ½ ∫_Y [ψ bar] D_{R. S.} &psu;d_vol

where

d_vol = d¹¹ x[squareroot of –g]

[R hat] is the scalar curvature of Y, G₄ is the four-form field strength which, when cohomologically trivial, is equal to dC₃. The fermions involve the kinetic action of &psi_M involving the Rarita-Schwinger operator D_{R. S.}. You can view D_{R. S.} as the Dirac operator coupled to the vector bundle associated to the virtual bundle

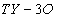
TY – 3[curly O]

where the [curly O] factors correspond to subtraction of ghosts. I_coupling corresponds to the coupling of &psi_M to G₄, as well as quartic &psi_M self-couplings.

The source-free Bianchi identity and equation of motion are

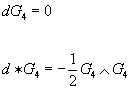
dG₄ = 0

d * G₄ = -½G₄ ∧ G₄

which can be modified by adding sources, such as the M2-brane and M5-brane. They have worldvolumes [curly W]₃ and [curly W]₆ respectively, by an embedding in spacetime Y. There are also one-loop corrections that, for example, modify the right hand side of the above equation by the topological quantity

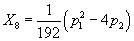
X₈ = (1/192)(p₁² - 4p₂))

given in terms of the Pontryagin classes of the tangent bundle TY. The four-form of M-theory obeys the quantization condition

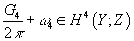
(G₄/2π) + ω₄ ∈ H⁴(Y; Z)

where ω₄ is the fourth Stiefel-Whitney class of the tangent bundle TY. In the orientable case

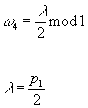
ω₄ = λ/2 mod 1

λ = p₁/2

The M-theory partition function is a product of factors that correspond to different parts of the action.

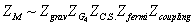
Z_M ~ Z_gravZ_G₄ Z_{C. S.} Z_fermi Z_coupling

We are interested in the topological part of the partition function, which means that we keep only the moduli associated with C₃ or G₄ but keep all the phases so that the part we are interested in is

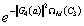
e^{-|| G₄(a) ||² Ω_M(C₃)}

Therefore, we do not consider Z_grav or Z_coupling. This theory can be viewed as having two kinds of fermions. First you have the spin ½ fermions in the E₈ gauge theory, and then you have the spin 3/2 Rarita-Schwinger fields in the supergravity. At the level of the action, you have

I_M = I_E₈ + I_{R. S.}/2

The low energy quantum measure of M-theory factorizes in terms of manifestly well-defined factors

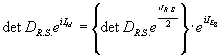
det D_{R. S.} e^iI_M = {det D_{R. S.} e^{iI_{R. S.}/2}} . e^iI_E₈

For the second factor, J = e^iE₈. If ∂Y ≠ 0, then J is not gauge-invariant, but is a section of a line bundle L^-1 over the space of C-fields over N = ∂Y.

The expression G₄ = dC₃ is not valid globally, and C₃ is not a well-defined differential form, implying that you have to be careful in defining the topological part I_{C. S.} of the action I₁₁. The way around this is to lift to twelve dimensions, and look at the action.

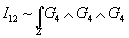
I₁₂ ~ ∫_Z G₄ ∧ G₄ ∧ G₄

over a twelve dimensional manifold Z. The full Chern-Simons coupling of M-theory is associated with I₁₂, which is well-defined and independent of the choice of Z and the extension of G₄. The action can be written as

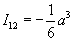
I₁₂ = -(1/6)a³

where a is the cohomology class of [G₄/2π]. Witten showed that there are two modifications to this. First of all,

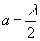
a - λ/2

is an integral, and second of all, we have to include

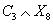
C₃ ∧ X₈

Introduce an E₈ bundle V on Z whose characteristic class ω obeys

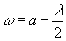
ω = a - λ/2

Witten showed that

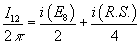
I₁₂/2π = i(E₈)/2 + i(R. S.)/4

and, including the above effects, the action takes the form

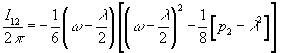
I₁₂/2π = -1/6(ω - λ/2)[(ω - λ/2)² - 1/8(p₂ - λ²)]

which is just I_{C. S.} with the gravitational corrections included. For the Rarita-Schwinger path integral, (1/2π)I₁₂ can be half integral in general, and has an anomaly that is cancelled from the one coming from the determinant of the Rarita-Schwinger operator det D_{R. S.}. The combination shows up as

det D_{R. S.} e^{iI_{R. S.}/2}

The Rarita-Schwinger operator can be viewed as the Dirac operator coupled to TX – 2[curly O], since Y is a circle bundle over X, or equivalently to TZ – 4[curly O] in twelve dimensions. Overall, you have the factor

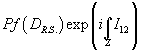
Pf(D_{R. S.}) exp(i∫_Z I₁₂)

where Pf(D_{R. S.}) is a vector in a Pfaffian line, so the above can be factorized into a modulus | Pf(D_{R. S.}) | and a phase

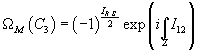
Ω_M(C₃) = (-1)^{I_{R. S.}/2} exp (i ∫_Z I₁₂)

Using the Atiyah-Patodi-Singer (APS) index theorem, you can relate the action to an index corrected by the reduced eta invariant

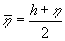
[η bar] = (h + η)/2

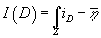
I(D) = ∫_Z i_D - [η bar]

so that the relevant integral in twelve dimensions can be written as

∫_Z I₁₂/2π = ½ I_E₈ + ¼ I_{R. S.} + (h_E₈ + η_E₈)/4 + (h_{R. S.} + η_{R. S.})/8

Now the factor (-1)^{I_{R. S.}} cancels the one coming from the index theorem, and taking into account the fact that the index is even, the phase is

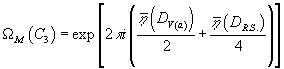
Ω_M(C₃) = exp[2πi ([η bar](D_V(a))/2 + [eta; bar](D_{R. S.})/4)]

The Riemannian metric on the circle bundle Y is

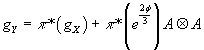
g_Y = π*(g_X) + π*(e^2φ/4)A ⊗ A

where g_X is the Riemannian metric on X, e^2φ/3 is the norm of the Killing vector along S¹, which in this trivialization is given by ∂z, φ is the dilaton, which is a real function on X, and A is a connection 1-form on the circle bundle Y. The component of the curvature in the direction of the circle action is

R₁₁ = e^2φ/3 = g_s^2/3

This choice of Riemannian metric is compatible with the principle bundle structure in the sense that the given circle bundle action acts on the isometries of Y. Performing a rescaling to the above metric, the desired metric ansantz for Type IIA is

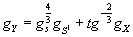
g_Y = g_s^4/3 g_S¹ + tg^-2/3 g_X

in the limit t → ∞, then g_s → 0.

The reduction of the 4-form G₄ on Y gives rise to two differential forms on X, the Neveu-Schwarz 3-form H₃, and the Ramond-Ramond 4-form F₄. This is obtained as follows, setting the dilaton to a constant for simplicity.

For an oriented S¹ bundle with first Chern class

c₁(Y) = F₂ = dA ∈ H²(X, Z)

you have a long exact sequence in cohomology called the Gysin sequence

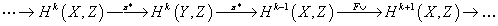
... → H^k(X, Z) →^π* H^k(Y, Z) →^π* H^{k – 1}(X, Z) →^F∪ H^{k + 1}(X, Z) → ...

If k = 4, you see that

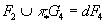
F₂ ∪ π_* G₄ = dF₄

where F₄ is some differential form on X. It follows that

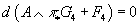
d(A ∧ π_* G₄ + F₄) = 0

Therefore, setting H₃ = π_* G₄, we see that H₃ is a closed form. Noting that π_*(A) = 1, we get the equation on Y, where it is understood that forms on X are pulled back to Y via π.

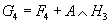
G4 = F₄ + A ∧ H₃

The curvature 2-form F₂ = dA is basic. It is horizontal, i_vF₂ = 0, and invariant, L_vF₂ = 0, where v is a vertical vector. In a local trivialization of the circle bundle where A = dz + θ, where θ is the connection on X, the above two conditions mean that F₂ has no dz component, and that it does not depend explicitly on z. Similarly, G₄ can be written in the given trivialization as

G₄ = F₄ + dz ∧ H₃