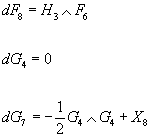
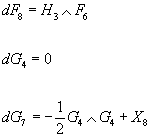
dF8 = H3 ∧ F6
dG4 = 0
dG7 = -½G4 ∧ G4 + X8
where F8 = *10F2, F6 = *10F4, G7 = *11G4, and X8 is a basic differential form of degree 8 on Y, which is a Chern-Simons correction factor. By applying the de Rham differential on the last of the above equations, you can see that X8 is a closed form. The one-loop coupling ∫ C3 ∧ X8 reduces to ∫ B2 ∧ X8. When X8 = 0, and G4 is proportional to a volume form of a four-dimensional factor in Y, this is the Freund-Rubin ansatz. When G4 is a flux through four-cycles in Y, there are solutions with X8 ≠ 0 for different choices of Y. The Bianchi identity dG4 = 0 reduces to the Bianchi identities for the RR 4-form, NS 3-form, and the RR 2-form field strengths.

dF4 = H3 ∧ F2
dH3 = 0
dF2 = 0
From general principles, you can write G7 = H7 + A ∧ F6 where H7 and F6 are basic forms on Y. This is consistent with
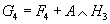
G4 = F4 + A ∧ H3
since you can show that

iv(*11F4) = *10F4
iv(*11(A ∧ H3)) = 0
You can use

dG7 = -½G4 ∧ G4 + X8
to show that
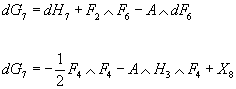
dG7 = dH7 + F2 ∧ F6 - A ∧ dF6
dG7 = -½F4 ∧ F4 - A ∧ H3 ∧ F4 + X8
Eliminating dG7 from the above equations, you get
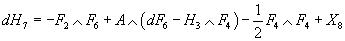
dH7 = -F2 ∧ F6 + A ∧ (dF6 - H3 &and F4) – ½F4 ∧ F4 + X8
All the terms in the above equation, except for the term involving A, are differential forms. Therefore, contracting the terms of the above equation with the vertical vector field v and using the fact that iv(A) = 1 and

iv(dF6 - H3 ∧ F4) = 0
we deduce the corresponding ten-dimensional Bianchi identities on X
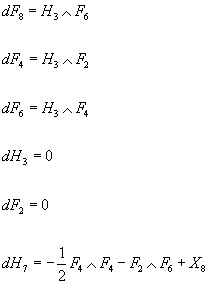
dF8 = H3 ∧ F6
dF4 = H3 ∧ F2
dF6 = H3 ∧ F4
dH3 = 0
dF2 = 0
dH7 = -½F4 ∧ F4 - F2 ∧ F6 + X8
From G4 ∈ Ω4(Y) satisfying the eleven-dimensional Bianchi identities, we obtain F = F2 + F4 + F6 + F8 ∈ Ωeven(X) satisfying (d – H3 ∧) F = 0, where we observe that F0 = 0 since H3 is not exact, and F8 ∧ H3 = 0 for dimensional reasons. Therefore, F determines a class in the twisted cohomology Heven(X, H3) where

H[dot](X, H3)
is the twisted cohomology, which is by definition, the cohomology of the Z2-graded complex
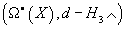
(Ω[dot](X), d – H3 ∧)
where the de Rham differential is replaced by
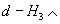
d – H3 ∧
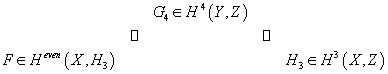
We are dealing with Dirac operators coupling to certain vector bundles. We are interested in the general case where the vector bundles are not lifted from the base. First of all, you have the twisting by the tangent bundle which leads to the Rarita-Schwinger operator. In this case, you are dealing with natural bundles which are not lifted from the base. Second of all, you also have the Dirac operator coupled to an E8 vector bundle. In this case, you want to consider it as not lifted from X. Therefore, you have eta-forms in the adiabatic limit of the reduced eta invariant of that Dirac operator.
First we’ll look at the Rarita-Schwinger operator DR. S.. There are two contributions, one from h, and one from η. In 8n + 2 dimensions
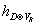
hD ⊗ VR
is a topological invariant mod 2. For the contribution from h, the idea is to try to relate the spectrum on Y to that of X.
E. Diaconescu, G. Moore, and E. Witten chose functions Φ that transform as

Φ → e-ikθ Φ
under an S1-rotation by an angle θ. The choice of functions depends on whether Y is compact or not. In the compact case, you can choose the functions to be smooth L2(Y) with respect to the metric that respects the circle bundle. In the case, X and Y are not compact, you can decompose the eta function as a sum over contributions from a given k. For k = 0, the phase is the same as the trivial circle bundle
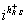
ihR. S.+
where + refers to positive chirality, and for k ≠ 0, there is no contribution from h. The contribution from η, derived by Diaconescu, Moore, and Witten is

η(s)/2 = | R |s [summation over k from 1 to ∞] (ak-(s – 1) + bk-(s – 3) + ck-(s – 5))
where the coefficients a, b, and c are given in terms of characteristic classes.
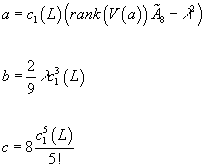
a = c1(L)(rank (V(a)) [A tilde]8 - λ2)
b = (2/9) λ c13(L)
c = 8c15(L)/5!
Then the above contributions combine in [η bar]R. S..
Now let’s look at the E8-coupled Dirac operator D on Y. We’ll use the method of J. Bismut, J. Cheeger, and X. Dai for calculating the adiabatic limit of the reduced eta invariant. Let’s say RX is the curvature of X, and SX is its spin connection ∇X induced from the Levi-Civita connection on X. Associated to the principle E8 bundle P on X, you have a Hermitian vector bundle V(a) with a unitary connection ∇V(a). Then the bundle SX ⊗ V(a) has a tensor product connection
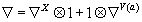
∇ = ∇X ⊗ 1 + 1 ⊗ ∇V(a)
A natural representation of C1(Xp) on SXp can be extended to a representation on SX ⊗ V(a). Corresponding to the scaled metric tgX, you have the Dirac operator DV(a)+, whose reduced eta invariant, when taken mod Z, was shown by Bismut, Cheeger, and Dai to be independent of t, and has a value of half the index of DV(a). When ker DY/X is a vector bundle on X, you can use it to twist DX. The connection on ker DY/X is obtained as the projection of a unitary connection on the infinite-dimensional bundle

ε = L2(π-1(X), Sπ-1(X))
of smooth spinor sections along the S1 fiber. For x ∈ X, you have
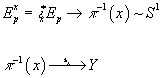
Epx = ix*Ep → π-1(X) ~S1
π-1(X) →Y
The assumption that Ker DY/X is a vector bundle on X implies that there is no spectral flow for the family of Dirac operators on the fibers DY/X. This means that there are no anomalies in this situation. Therefore, the adiabatic limit of the eta invariant on Y has a closed formula given by
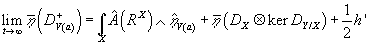
[limit of t → ∞] [η bar] (DV(a)+) = ∫X [A hat] (RX) ∧ [η hat]V(a) + [η bar] (DX ⊗ ker DY/X) + ½h’
where [A hat](RX) is the [A hat] invariant polynomial applied to the curvature, ½h’ is a spin cobordism invariant, and the eta-form is a differential form on X given by
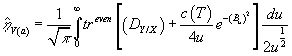
[η hat]V(a) = 1/[squareroot of π] ∫0∞ treven [(DY/X + c(T)/4u) e-(Bu)2] du/2u½
where

Bu = ∇V(a) + u½ DY/X - c(T)/4u½
is the Bismut superconnection, where c is the Clifford multiplication, and T is the torsion of the connection. The eta-form is of even degree, and can be divided into homogenous even parts as
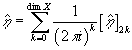
[η hat] = [summation over k from 0 to dim X] 1/(2πi)k [η hat]2k
and has the η-invariant of the Dirac operator along the fiber for the 0-form component.
This form comes from the spectral correction to the families version of the Atiyah-Patodi-Singer nonlocal elliptic boundary problem. Remember that Z is a disk bundle over X, where the boundary is the circle bundle Y over X. The Bismut-Cheeger-Dai theorem then says
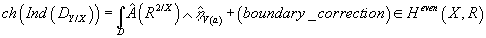
ch(Ind(DZ/Y)) = ∫D [A hat] (RZ/X) ∧ [η hat]V(a) + (boundary correction) ∈ Heven(X, R)
where D is the disk which is the fiber of Z, DZ/X is the family of twisted Dirac operators along the fibers of Z that are parametrized by X with the Atiyah-Patodi-Singer boundary conditions, and RZ/X is the curvature of the vertical tangent bundle on Z. The differential

d[η hat] = ∫S1 [A hat] (RY/X) ∧ tr (e-(1/2πi)RV(a))
is closed, not exact, and represents the odd Chern class of DY/X, RY/X is the curvature of the connection of the vertical tangent bundle Y, and RV(a) is the curvature of the unitary connection on V(a). After integrating over the fiber, you get an odd degree differential form on X. This implies that the higher spectral flow vanishes.
Let’s look at the following diagram.
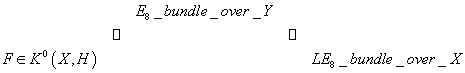
Compare to the similar diagram I gave earlier. A. Adams and J. Evslin suggested that the E8 bundle in M-theory can be related to an LE8 bundle in Type IIA on X. Starting from the principle E8 bundle over Y, the dimensional relation of M-theory to Type IIA gives a LE8 bundle P’ in ten dimensions characterized by the 3-form

H3 = ∫S1 G4
Remember I gave the following diagram
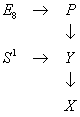
The following diagrams are related.

Notice that since E8 is an approximate K(Z, 3) up to dimension 14, it follows that principle E8 bundles over Y are classified by H4(Y, Z). Specifically, the characteristic class of an E8 bundle is the restriction of the first Pontryagin class p1 to the 4-spheres in the 4-skeleton of the base manifold.
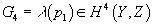
G4 = λ(p1) ∈ H4(Y, Z)
Then the class on LE8 is
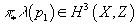
π*λ(p1) ∈ H3(X, Z)
There exists a LE8 bundle, unique up to isomorphism, such as the Diximier-Douady class
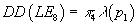
DD(LE8) = π*λ(p1)
For m ∈ X, π-1(m) = S1, you have
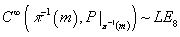
C∈(π-1(m), P |π-1(m)) ~ LE8
This gives the fibration above with
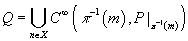
Q = [union over m ∈ X] C∞(π-1(m), P |π-1(m))
So DD(Q) = π*λ(p1) = H3. The obstruction to lifting the LE8 bundle Q to an [LE8 hat] bundle P’ covering Q is the Diximier-Douady class.
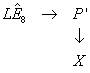
Such a lift is possible only when H3 = dB2. Therefore, in the presence of F0, only the trivial case, in the sense of the NS 3-form, can be seen in the loop picture.
Before I described how you can derive a 4-form F4 on X from a 4-form G4 on Y. Remember that F2 = dA, and considering the inhomogeneous even degree form F = F2 + F4 + F6 + F8 where F8 = *10F2 and F6 is obtained from dimensional reduction G7 = *G4. F is d – H closed. Then using the fact that the twisted Chern character
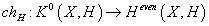
chH : K0(X, H) → Heven(X, H)
is an isomorphism over the reals, you get an element
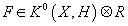
F ∈ K0(X, H) ⊗ R
We don’t know at this time how to lift this to a class in K0(X, H).
When you have branes and H-flux, the RR fields F are determined by the twisted K-theory classes x &isin K(X, H), and by the twisted Chern map
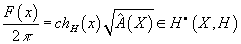
F(x)/2π = chH(x) [squareroot of [A hat](x)] ∈ H[dot](X, H)
where [A hat] is the A-roof genus. It turns out that the conjugate of x, [x bar] ∈ (X, -H)
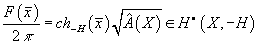
F([x bar])/2π = ch-H [squareroot of [A hat](x)] ∈ H[dot](X, -H)
Setting
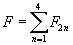
F = [summation over n from 1 to 4] F2n
for the gauge field strengths, the RR field equations of motion can be written as

dF = H3 ∧ F
In order to make the RR field strengths homogeneous of degree zero, you can use K-theory with coefficients in
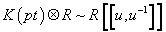
K(p+) ⊗ R[[u, u-1]]
Where the inverse Bott element u ∈ k2(pt) has degree 2, and looks at the corresponding Chern character as a homomorphism of Z-graded rings.

ch : K(X, H) → Heven(X, H; R[[u, u-1]]
Then the total RR field strength is written as
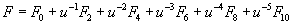
F = F0 + u-1F2 + u-2F4 + u-3F6 + u-4F8 + u-5F10
In other words, the RR field equations of motion on the level of differential forms says that the RR fields determine elements in the twisted cohomology H[dot](X, H). At the level of cohomology, this implies
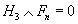
H3 ∧ Fn = 0
In KH, or actually the Atiyah-Hirzebruch spectral sequence (AHSS), this becomes
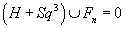
(H + Sq3) ∪ Fn = 0
Diaconescu, Moore, and Witten conjecture that the M-theory partition function on a circle bundle can be written in terms of fields satisfying the above equation.
The cup product pairing in twisted K-theory with the standard index pairing of elements of K-theory with the Dirac operator explains the upper horizontal arrows in the diagram.

The bottom horizontal arrows are cup product in the twisted cohomology followed by cup product by [A hat](X) and by integration. By the Atiyah-Singer index theorem, the above diagram commutes. Therefore, the normalization given to the Chern character in the definition of F(x)/2π makes the pairings in twisted cohomology isometric.
Witten pointed out that the self-duality *F = F is more subtle than that. It turns out it’s not possible to impose a classical quantization law on the periods of the self-dual p-form. This is because you can’t simultaneously measure anticommuting periods, which are the ones where the intersection number is nonzero. The way around this is to interpret the self-duality as a statement in the quantum theory and the sum over half the fluxes, meaning over a maximum set of commuting periods. Therefore, we need a phase space in the twisted K-theory with a polarization or Lagrangian subspace that naturally splits the forms in half. The lattice is
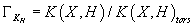
ΓKH = K(X, H)/K(X, H)tors
This is isomorphic to the image of the modified Chern character homomorphism of Z2-graded rings.
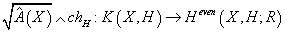
[squareroot of [A hat](X)] ∧ chH : K(X, H) → Heven(X, H; R)
where the kernel is K(X, H)tors, the torsion subgroup. The lattice is unimodular by Poincare duality in twisted K-theory.
To summarize, you can relate the fields of M-theory to those of Type IIA in the large volume limit, for a nontrivial circle bundle, and in the presence of nontrivial NS flux H3. You can derive the RR fields of Type IIA from the M-theory 4-form G4 satisfying Maxwell-like equations. Those fields are elements in twisted cohomology Heven(X, H3).
Up until this point, we’ve been discussing the relationship between K-theory and string theory, specifically using K-theory to classify D-brane charges. One problem with that is that Diaconsecu, Moore, and Witten pointed out that the twisted K-theory classification is not compatible with the S-duality covariance in Type IIB string theory. For this reason, Hisham Sati and Igor Kriz proposed that instead of twisted K-theory, Type IIB string theory should instead be classified by elliptic cohomology. Therefore, for the remainder of this paper, I’m going to shift gears, and discuss the relation between elliptic cohomology and string theory. First I have to explain what elliptic cohomology is. Elliptic cohomology is a Taylor expansion of the formal group laws of an elliptic curve over a commutative ring. An elliptic curve is a type of cubic curve whose solutions are confined to a region of space that is topologically equivalent to a torus. The Weierstrass elliptic function p(2; g2, g3) describes how to get from this torus to the algebraic form of an elliptic curve. Formally, an elliptic curve over a field K is a nonsingular cubic curve in two variables f(X, Y) = 0, with a K-rational point, which may be at infinity. The field K is usually taken to be the complex numbers, C, reals, R, rationals, Q, algebraic extensions of Q, p-adic numbers, Qp, or a finite field. By an appropriate change of variables, a general elliptic curve over a field, with a field characteristic not 2 or 3, is a general cubic curve
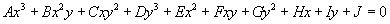
Ax3 + Bx2y + Cxy2 + Dy3 + Ex2 + Fxy + Gy2 + Hx + Iy + J = 0
where A, B, C,…,J are elements of K, and can be written in the form y2 = x3 + ax + b where the right hand side has no repeated factors.
Any elliptic curve not of characteristic 2 or 3 can also be written in Legendre normal form
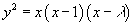
Y2 = x(x – 1)(x - λ)
If K has field characteristic three, it can be written as y2 = x3 + Ay2 + Bx + C. If K has field characteristic two, it can be written in Weierstrass form y2 + Ay = x3 + Bx2 + Cxy + Dx + E. An elliptic curve of form y2 = x3 + n, where m is an integer, is called a Mordell curve.
An elliptic curve is a doubly periodic function with periods 2ω1 and 2ω2 such that
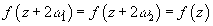
F(z + 2ω1) = f(z + 2ω2) = f(z)
which is analytic and has no singularities except for poles in the finite part of the complex plane. The half-plane ratio τ = ω2/ω1 must not be purely real, because if it is, the function reduces to a singly periodic function if τ is rational, and a constant if τ is irrational. ω1 and ω2 are labeled such that I[τ] = I[ω2/ω1] > 0, where I[z] is the imaginary part. A cell of an elliptic function is defined as a parallelogram region in the complex plane in which the function is not multi-valued. Elliptic functions obey the following properties.
1. The number of poles in a cell is finite.
2. The number of roots in a cell is finite.
3. The sum of complex residues in any cell is zero.
4. Liouville elliptic theorem – An elliptic function with no poles in a cell is a constant.
5. The number of zeroes of f(z) – c, called the order, equals the number of poles of f(z).
6. The simplest elliptic function has order two, since a function of order one would not have a simple irreducible pole, which would need a nonzero residue, which would violate property 3.
7. Elliptic functions with a single pole of order two with a complex residue zero are called Weierstrass elliptic functions. Elliptic functions with two simple poles having residues a0 and –a0 are called Jacobi elliptic functions.
8. Any elliptic function is expressible in terms of either Weierstrass elliptic functions or Jacobi elliptic functions.
9. The sum of the affixes of roots equals the sum of affixes of poles.
10. An algebraic relationship exists between any two elliptic functions with the same periods.
The elliptic functions are inversions of the elliptic integrals. The two standard forms of these functions are Jacobi elliptic functions and Weierstrass elliptic functions. Jacobi elliptic functions arise as solutions to differential equations of the form
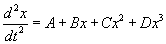
dx2/dt2 = A + Bx + Cx2 + Dx3
and Weierstrass elliptic functions arise as solutions to differential equations of the form
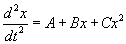
d2x/dt2 = A + Bx + Cx2
The reason for the name “elliptic” is because elliptic functions generalize the trigonometric functions from circles to ellipses. Elliptic curves show up in many branches of mathematics, such as Wiles’ proof of Fermat’s Last Theorem. Elliptic curves are also important in the Monster Moonshine Conjecture, or Monstrous Moonshine. What’s amazing is that in 2007, Edward Witten related Monstrous Moonshine directly to string theory. Witten actually used the Monster group to calculate the entropy of black holes, and got results consistent with Hawking’s semiclassical approximation, but I don’t want to get too far away from the subject of this paper.
A formal group law is a formal power series behaving as if it were the product of a Lie group. They were first defined in 1946 by S, Bochner. Formal group laws are intermediate between Lie groups and Lie algebras. A one-dimensional formal group law over a commutative ring R is a power series F(x, y) with coefficients in R such that
1. F(x, y) = x + y + terms of higher degree
2. Associativity - F(x, F(y, z)) = F(F(x, y), z)
The simplest example is the additive formal group law F(x, y) = x + y. The basic idea is that F should be something like the formal power series expansion of the product of a Lie group where we choose coordinates so that the identity of the Lie group is the origin.
More generally, an n-dimensional formal group law is a collection of n power series Fi(x1, x2,…xn, y1, y2,…yn) in 2n variables such that
3. F(x, y) = x + y + terms of higher degree
4. Associativity - F(x, F(y, z)) = F(F(x, y), z)
where F = (F1, F2,…Fn), x = (x1, x2,…xn), etc.
The formal group law is called commutative if F(x, y) = F(y, x). One dimensional formal group laws are usually commutative. They are commutative unless the ring r contains a nonzero nilpotent torsion element. You don’t have to have an axiom analogous to the existence of an inverse for groups since it turns out that this follows automatically from the definition of a formal group law. In other words, you can always find a unique power series G such that F(x, G(x)) = 0. A homomorphism from a formal group law F of dimension m to a formal group law G of dimension n is a collection f of n power series in m variables such that
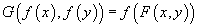
G(f(x), f(y)) = f(F(x, y))
A homomorphism with an inverse is called an isomorphism. An isomorphism with f(x) = x + higher degree terms is called a strict isomorphism. Two formal group laws with an isomorphism between them are essentially the same. They differ only by a change of coordinates.